Published online by Cambridge University Press: 22 January 2016
Let 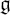 be a Kac-Moody-Borcherds algebra on a field
be a Kac-Moody-Borcherds algebra on a field 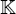 associated to a symetrizable matrix and with Cartan subalgebra
associated to a symetrizable matrix and with Cartan subalgebra 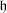 . Let
. Let 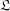 be an ad
be an ad 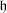 -invariant subalgebra such that the restriction to
-invariant subalgebra such that the restriction to 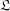 of the standard bilinear form is nondegenerate. We show that the root system Ψ of
of the standard bilinear form is nondegenerate. We show that the root system Ψ of 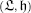 is a subsystem according to [Ba] of
is a subsystem according to [Ba] of 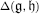 . Moreover, if a subsystem Ω satisfies some conditions (i.e. Ω is “réduit et presque-clos”) of Ψ, we construct inside of
. Moreover, if a subsystem Ω satisfies some conditions (i.e. Ω is “réduit et presque-clos”) of Ψ, we construct inside of 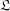 a Kac-Moody-Borcherds algebra with root system Ω.
a Kac-Moody-Borcherds algebra with root system Ω.
Let k be a subfield of 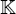 . We prove similar results in the case of an action of a finite group of k-semi-automorphisms. In particular, we obtain a generalization to the Kac-Moody case of a result by Borel and Tits.
. We prove similar results in the case of an action of a finite group of k-semi-automorphisms. In particular, we obtain a generalization to the Kac-Moody case of a result by Borel and Tits.
Let 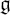 be an almost-k-split form of a Kac-Moody algebra. We construct a Kac-Moody k-algebra with root system similar to the system of
be an almost-k-split form of a Kac-Moody algebra. We construct a Kac-Moody k-algebra with root system similar to the system of 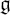 (save on some multiples of certain roots).
(save on some multiples of certain roots).