Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T22:02:35.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Numerical Criteria for the Nash Problem on Arcs for Surfaces

Published online by Cambridge University Press:  11 January 2016

Marcel Morales
Marcel Morales*
Affiliation:
Université de Grenoble I, Institut Fourier, UMR 5582, B.P.74 38402, Saint-Martin, D’Hères Cedex, and IUFM de Lyon, 5 rue Anselme 69317 Lyon Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, O) be a germ of a normal surface singularity, π: 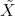→ X be the minimal resolution of singularities and let A = (ai,j) be the n × n symmetrical intersection matrix of the exceptional set of 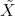In an old preprint Nash proves that the set of arcs on a surface singularity is a scheme 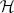, and defines a map 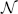from the set of irreducible components of 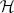to the set of exceptional components of the minimal resolution of singularities of (X,O). He proved that this map is injective and ask if it is surjective. In this paper we consider the canonical decomposition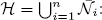

  • • For any couple (Ei,Ej) of distinct exceptional components, we define Numerical Nash condition (NN(i,j)). We have that (NN(i,j)) implies 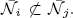In this paper we prove that (NN(i,j)) is always true for at least the half of couples (i,j).

  • • The condition (NN(i,j)) is true for all couples (i,j) with i ≠ j, characterizes a certain class of negative definite matrices, that we call Nash matrices. If A is a Nash matrix then the Nash map N is bijective. In particular our results depend only on A and not on the topological type of the exceptional set.

  • • We recover and improve considerably almost all results known on this topic and our proofs are new and elementary.

  • • We give infinitely many other classes of singularities where Nash Conjecture is true.

The proofs are based on my old work [8] and in Plenat [10].

Keywords

14B0514E1514J1732SXX
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 191 , 2008 , pp. 1 - 19
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2008

References

[1] Denef, J. and Loeser, F., Germs of arcs on singular varieties and motivic integration, Inv. Math., 135 (1999), 201–232.Google Scholar
[2] Fernandez-Sanchez, J., Equivalence of the Nash conjecture for primitive and sandwiched singularities, Proc. Amer. Math. Soc., 133 (2005), 677–679.Google Scholar
[3] Grauert, H., Uber modifikationen und exceptionnelle analytische Mengen, Math. Annalen, 146 (1962), 331–368.Google Scholar
[4] Gonzalez-Sprinberg, G. and Lejeune-Jalabert, M., Families of smooth curves on surface singularities and wedges, Annales Polonici Mathematici, LXVII.2 (1997), 179–190.Google Scholar
[5] Ishii, S. and Kollar, J., The Nash problem on arc families of singularities, Duke Math. J., 120 (2003), no. 3, 601–620.Google Scholar
[6] Lejeune-Jalabert, M., Courbes tracées sur un germe d’hypersurface, Amer. J. of Math., 112 (1990), 525–568.CrossRefGoogle Scholar
[7] Lejeune-Jalabert, M. and Reguera, A., Arcs and wedges on sandwiched surfaces singularities, Amer. J. of Math., 121 (1999), 1191–1213.Google Scholar
[8] Morales, M., Clôoture intégrale d’idéaux et anneaux gradués Cohen-Macaulay, Géo-métrie algébrique et applications, La Rabida 1984 (Aroca, J-M., et als, eds.), Hermann, pp. 15–172.Google Scholar
[9] Nash, J. F. Jr., Arcs structure of singularities, Duke Math. J., 81 (1995), no. 1, 31–38.Google Scholar
[10] Plénat, C., A Propos du problème des arcs de Nash, Ann. Inst. Fourier., 55 (2005), no. 3, 805–823.Google Scholar
[11] Plénat, C., Résolution du problème des arcs de Nash pour les points doubles rationnels Dn , Thèse Univ. Paul Sabatier. Toulouse, 2004.Google Scholar
[12] Plénat, C. and Popescu-Pampu, P., A class of non-rational surfaces singularities for which the Nash map is bijective, Bulletin Soc. Math. France, to be published.Google Scholar
[13] Reguera, A., Families of Arcs on rational surface singularities, Manuscripta Math., 88 (1995), 321–333.CrossRefGoogle Scholar
[14] Reguera, A., A curve selection lemma in spaces of arcs and the image of the Nash map, Compos. Math., 142 (2006), no. 1, 119–130.Google Scholar