Article contents
Some Families of Componentwise Linear Monomial Ideals
Published online by Cambridge University Press: 11 January 2016
Abstract
Let R = k[x1,…,xn] be a polynomial ring over a field k. Let J = {j1,…,jt} be a subset of {1,…, n}, and let mJ ⊂ R denote the ideal (xj1,…,xjt). Given subsets J1,…,Js of {1,…, n} and positive integers a1,…,as, we study ideals of the form 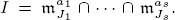 These ideals arise naturally, for example, in the study of fat points, tetrahedral curves, and Alexander duality of squarefree monomial ideals. Our main focus is determining when ideals of this form are componentwise linear. Using polymatroidality, we prove that I is always componentwise linear when s ≤ 3 or when Ji ∪ Jj = [n] for all i ≠ j. When s ≥ 4, we give examples to show that I may or may not be componentwise linear. We apply these results to ideals of small sets of general fat points in multiprojective space, and we extend work of Fatabbi, Lorenzini, Valla, and the first author by computing the graded Betti numbers in the s = 2 case. Since componentwise linear ideals satisfy the Multiplicity Conjecture of Herzog, Huneke, and Srinivasan when char(k) = 0, our work also yields new cases in which this conjecture holds.
These ideals arise naturally, for example, in the study of fat points, tetrahedral curves, and Alexander duality of squarefree monomial ideals. Our main focus is determining when ideals of this form are componentwise linear. Using polymatroidality, we prove that I is always componentwise linear when s ≤ 3 or when Ji ∪ Jj = [n] for all i ≠ j. When s ≥ 4, we give examples to show that I may or may not be componentwise linear. We apply these results to ideals of small sets of general fat points in multiprojective space, and we extend work of Fatabbi, Lorenzini, Valla, and the first author by computing the graded Betti numbers in the s = 2 case. Since componentwise linear ideals satisfy the Multiplicity Conjecture of Herzog, Huneke, and Srinivasan when char(k) = 0, our work also yields new cases in which this conjecture holds.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2007
References
- 8
- Cited by


