Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bouchard, Vincent
Creutzig, Thomas
Diaconescu, Duiliu-Emanuel
Doran, Charles
Quigley, Callum
and
Sheshmani, Artan
2017.
Vertical D4–D2–D0 Bound States on K3 Fibrations and Modularity.
Communications in Mathematical Physics,
Vol. 350,
Issue. 3,
p.
1069.
Bruinier, Jan Hendrik
and
Schwagenscheidt, Markus
2017.
Algebraic formulas for the coefficients of mock theta functions and Weyl vectors of Borcherds products.
Journal of Algebra,
Vol. 478,
Issue. ,
p.
38.
Westerholt-Raum, Martin
2017.
Products of vector valued Eisenstein series.
Forum Mathematicum,
Vol. 29,
Issue. 1,
p.
157.
Scheithauer, Nils R.
2017.
Automorphic products of singular weight.
Compositio Mathematica,
Vol. 153,
Issue. 9,
p.
1855.
Yang, Tonghai
and
Ye, Dongxi
2018.
Weakly holomorphic modular forms on $$\Gamma _{0}(4)$$ and Borcherds products on unitary group $$\mathrm{U}(2,1)$$.
Research in Number Theory,
Vol. 4,
Issue. 1,
Schwagenscheidt, Markus
2018.
Eisenstein series for the Weil representation.
Journal of Number Theory,
Vol. 193,
Issue. ,
p.
74.
Gritsenko, V. A.
and
Wang, H.
2019.
Antisymmetric paramodular forms of weight 3.
Sbornik: Mathematics,
Vol. 210,
Issue. 12,
p.
1702.
Ma, Shouhei
2019.
Quasi‐pullback of Borcherds products.
Bulletin of the London Mathematical Society,
Vol. 51,
Issue. 6,
p.
1061.
Gritsenko, Valerii Alekseevich
and
Wang, Haowu
2019.
Антисимметричные парамодулярные формы веса 3.
Математический сборник,
Vol. 210,
Issue. 12,
p.
43.
Zhang, Yichao
2020.
Half-integral weight modular forms and modular forms for Weil representations.
manuscripta mathematica,
Vol. 163,
Issue. 3-4,
p.
507.
Wang, Haowu
2021.
Reflective Modular Forms: A Jacobi Forms Approach.
International Mathematics Research Notices,
Vol. 2021,
Issue. 3,
p.
2081.
Bruinier, Jan Hendrik
and
Schwagenscheidt, Markus
2021.
Theta lifts for Lorentzian lattices and coefficients of mock theta functions.
Mathematische Zeitschrift,
Vol. 297,
Issue. 3-4,
p.
1633.
Möller, Sven
2021.
Natural Construction of Ten Borcherds-Kac-Moody Algebras Associated with Elements in $$M_{23}$$.
Communications in Mathematical Physics,
Vol. 383,
Issue. 1,
p.
35.
Stein, Oliver
2022.
On analytic properties of the standard zeta function attached to a vector-valued modular form.
Research in Number Theory,
Vol. 8,
Issue. 4,
Wang, Haowu
2022.
Reflective modular forms on lattices of prime level.
Transactions of the American Mathematical Society,
Ye, Dongxi
2022.
Difference of a Hauptmodul for Γ0(N) and certain Gross-Zagier type CM value formulas.
Science China Mathematics,
Vol. 65,
Issue. 2,
p.
221.
Dittmann, Moritz
and
Wang, Haowu
2022.
Theta blocks related to root systems.
Mathematische Annalen,
Vol. 384,
Issue. 3-4,
p.
1157.
Schwagenscheidt, Markus
and
Williams, Brandon
2023.
Binary theta functions and Borcherds products.
Journal of Number Theory,
Vol. 249,
Issue. ,
p.
441.
Müller, Manuel K.-H.
2024.
Modular forms for the Weil representation induced from isotropic subgroups.
Journal of Number Theory,
Vol. 263,
Issue. ,
p.
206.
Strömberg, Fredrik
2024.
On liftings of modular forms and Weil representations.
Forum Mathematicum,
Vol. 36,
Issue. 1,
p.
33.


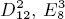 and to the Leech lattice.
and to the Leech lattice.