Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T05:20:25.619Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP

Part of: Lie algebras and Lie superalgebras Rings and algebras with additional structure Basic linear algebra

Published online by Cambridge University Press:  04 December 2019

G. I. LEHRER Open the ORCID record for G. I. LEHRER [Opens in a new window]  and
R. B. ZHANG Open the ORCID record for R. B. ZHANG [Opens in a new window]
G. I. LEHRER
Affiliation:
School of Mathematics and Statistics, University of Sydney, N.S.W.2006, Australia email [email protected]
R. B. ZHANG
Affiliation:
School of Mathematics and Statistics, University of Sydney, N.S.W.2006, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The first fundamental theorem of invariant theory for the orthosymplectic supergroup scheme 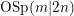$\text{OSp}(m|2n)$ states that there is a full functor from the Brauer category with parameter $m-2n$ to the category of tensor representations of 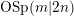$\text{OSp}(m|2n)$. This has recently been proved using algebraic supergeometry to relate the problem to the invariant theory of the general linear supergroup. In this work, we use the same circle of ideas to prove the second fundamental theorem for the orthosymplectic supergroup. Specifically, we give a linear description of the kernel of the surjective homomorphism from the Brauer algebra to endomorphisms of tensor space, which commute with the orthosymplectic supergroup. The main result has a clear and succinct formulation in terms of Brauer diagrams. Our proof includes, as special cases, new proofs of the corresponding second fundamental theorems for the classical orthogonal and symplectic groups, as well as their quantum analogues, which are independent of the Capelli identities. The results of this paper have led to the result that the map from the Brauer algebra 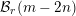${\mathcal{B}}_{r}(m-2n)$ to endomorphisms of 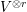$V^{\otimes r}$ is an isomorphism if and only if 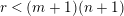$r<(m+1)(n+1)$.

MSC classification

Primary: 16W22: Actions of groups and semigroups; invariant theory 15A72: Vector and tensor algebra, theory of invariants 17B20: Simple, semisimple, reductive (super)algebras
Type
Article
Information
Nagoya Mathematical Journal , Volume 242 , June 2021 , pp. 52 - 76
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work has been supported by the Australian Research Council.

References

Atiyah, M., Bott, R. and Patodi, V. K., On the heat equation and the index theorem, Invent. Math. 19 (1973), 279–330.CrossRefGoogle Scholar
Baha Balantekin, A. and Bars, I., Representations of supergroups, J. Math. Phys. 22(8) (1981), 1810–1818.CrossRefGoogle Scholar
Berele, A., Invariant theory for matrices over the Grassmann algebra, Adv. Math. 237 (2013), 33–61.CrossRefGoogle Scholar
Berele, A. and Regev, A., Hook Young diagrams with applications to combinatorics and to representations of Lie superalgebras, Adv. Math. 64 (1987), 118–175.CrossRefGoogle Scholar
Deligne, P. and Morgan, J. W., “Notes on supersymmetry (following Joseph Bernstein)”, in Quantum Fields and Strings: A Course for Mathematicians, Vol. 1, 2 (Princeton, NJ, 1996/1997), American Mathematical Society, Providence, RI, 1999, 41–97.Google Scholar
Deligne, P., Lehrer, G. I. and Zhang, R. B., The first fundamental theorem of invariant theory for the orthosymplectic super group, Adv. Math. 327 (2018), 4–24.CrossRefGoogle Scholar
Ehrig, M. and Stroppel, C., Schur–Weyl duality for the Brauer algebra and the ortho-symplectic Lie superalgebra, Math. Z. 284(1–2) (2016), 595–613.CrossRefGoogle Scholar
Dondi, P. H. and Jarvis, P. D., Diagram and superfield techniques in the classical superalgebras, J. Phys. A 14(3) (1981), 547–563.Google Scholar
Goodman, R. and Wallach, N. R., Representations and Invariants of the Classical Groups, Cambridge University Press, Cambridge, 2003, third corrected printing.Google Scholar
Graham, J. J. and Lehrer, G. I., Cellular algebras, Invent. Math. 123 (1996), 1–34.CrossRefGoogle Scholar
Graham, J. J. and Lehrer, G. I., The representation theory of affine Temperley–Lieb algebras, Enseign. Math. (2) 44(3–4) (1998), 173–218.Google Scholar
Graham, J. J. and Lehrer, G. I., Diagram algebras, Hecke algebras and decomposition numbers at roots of unity, Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 479–524.CrossRefGoogle Scholar
Graham, J. J. and Lehrer, G. I., “Cellular algebras and diagram algebras in representation theory”, Representation Theory of Algebraic Groups and Quantum Groups, Advance Studies in Pure Mathematics 40, 141–173. Math. Soc. Japan, Tokyo, 2004.CrossRefGoogle Scholar
Kac, V., Lie superalgebras, Adv. Math. 26(1) (1977), 8–96.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., Strongly multiplicity free modules for Lie algebras and quantum groups, J. Algebra 306 (2006), 138–174.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., “A Temperley–Lieb analogue for the BMW algebra”, in Representation Theory of Algebraic Groups and Quantum Groups, Progress in Mathematics 284, Birkhäuser/Springer, New York, 2010, 155–190.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., The second fundamental theorem of invariant theory for the orthogonal group, Ann. of Math. (2) 176 (2012), 2031–2054.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., The Brauer category and invariant theory, J. Eur. Math. Soc. 17 (2015), 2311–2351.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., The first fundamental theorem of invariant theory for the orthosymplectic supergroup, Comm. Math. Phys. 349 (2017), 661–702.CrossRefGoogle Scholar
Lehrer, G. I., Zhang, H. and Zhang, R. B., A quantum analogue of the first fundamental theorem of invariant theory, Comm. Math. Phys. 301 (2011), 131–174.CrossRefGoogle Scholar
Procesi, C., Lie Groups. An Approach through Invariants and Representations, Universitext, Springer, New York, 2007, xxiv+596 pp.Google Scholar
Salam, A. and Strathdee, J., Super-gauge transformations, Nuclear Phys. B76 (1974), 477–482.CrossRefGoogle Scholar
Scheunert, M., The Theory of Lie Superalgebras; An Introduction, Lecture Notes in Mathematics 716, Springer, Berlin–Heidelberg–New York, 1979.CrossRefGoogle Scholar
Scheunert, M. and Zhang, R. B., The general linear supergroup and its Hopf superalgebra of regular functions, J. Algebra 254(1) (2002), 44–83.CrossRefGoogle Scholar
Sergeev, A., An analogue of the classical theory of invariants for Lie superalgebras, Funktsional. Anal. i Prilozhen. 26(3) (1992), 88–90; (Russian) translation in Funct. Anal. Appl. 26(3) (1992), 223–225.CrossRefGoogle Scholar
Sergeev, A., An analog of the classical invariant theory for Lie superalgebras. I, II, Michigan Math. J. 49(1) (2001), 113–146; 147–168.CrossRefGoogle Scholar
Varadarajan, V. S., Supersymmetry for Mathematicians: An Introduction, Courant Lecture Notes in Mathematics 11, New York University, Courant Institute of Mathematical Sciences, New York, 2004, American Mathematical Society, Providence, RI.Google Scholar
De Witt, B., “Supermanifolds”, in Cambridge Monographs on Mathematical Physics, 2nd ed., Cambridge University Press, Cambridge, 1992.Google Scholar
Zhang, Y., On the second fundamental theorem of invariant theory for the orthosymplectic supergroup, J. Algebra 501 (2018), 394–434.CrossRefGoogle Scholar