1. Introduction
Consider the following Cauchy problem:

The formal solution is given by
 $$ \begin{align*} u(t)=e^{it\Delta}u_0-i\int_0^te^{i(t-s)\Delta}F(u(s))ds. \end{align*} $$
$$ \begin{align*} u(t)=e^{it\Delta}u_0-i\int_0^te^{i(t-s)\Delta}F(u(s))ds. \end{align*} $$
If we want to establish the local existence with the initial data
![]() $u_0$
belonging to certain function space X, a crucial step is to consider the initial data in function spaces, which are invariant under linear propagator, that is, to establish the corresponding norm estimate for Schrödinger propagator on X of the following type:
$u_0$
belonging to certain function space X, a crucial step is to consider the initial data in function spaces, which are invariant under linear propagator, that is, to establish the corresponding norm estimate for Schrödinger propagator on X of the following type:
In the classical research of Schrödinger equation, the initial data
![]() $u_0$
are usually assumed to belong to an
$u_0$
are usually assumed to belong to an
![]() $L^2$
-based function spaces, such as the
$L^2$
-based function spaces, such as the
![]() $L^2$
-based Sobolev space
$L^2$
-based Sobolev space
![]() $(I-\Delta )^{\frac {-s}{2}}L^2$
or Besov space
$(I-\Delta )^{\frac {-s}{2}}L^2$
or Besov space
![]() $B^{2,q}_s$
. An important reason is that only
$B^{2,q}_s$
. An important reason is that only
![]() $p=2$
allows the estimate (1.1) to hold on
$p=2$
allows the estimate (1.1) to hold on
![]() $X=(I-\Delta )^{\frac {-s}{2}}L^p$
or
$X=(I-\Delta )^{\frac {-s}{2}}L^p$
or
![]() $X=B^{p,q}_s$
.
$X=B^{p,q}_s$
.
The situation changes if we replace the classical dyadic decomposition in the definition of Besov spaces by uniform decomposition. More precisely, if we use modulation space
![]() $X=M^{p,q}_s$
in the estimate (1.1), the following boundedness is valid [Reference Bényi, Gröchenig, Okoudjou and Rogers1], [Reference Wang, Zhao and Guo21]:
$X=M^{p,q}_s$
in the estimate (1.1), the following boundedness is valid [Reference Bényi, Gröchenig, Okoudjou and Rogers1], [Reference Wang, Zhao and Guo21]:
Due to this advantage of modulation space, many researchers have begun to use modulation space to study partial differential equations. We refer the reader to the pioneer works [Reference Bényi and Okoudjou2], [Reference Wang and Hudzik20] and to [Reference Bhimani and Haque3], [Reference Schippa17] for some recent progress.
Modulation spaces were introduced first by Feichtinger [Reference Feichtinger7] in 1983. It has been regarded as a basic and important class of function spaces in the field of time–frequency (see [Reference Gröchenig9]). Comparing with the classical Besov space
![]() $B^{p,q}_s$
, modulation space
$B^{p,q}_s$
, modulation space
![]() $M^{p,q}_s$
(see [Reference Triebel18] for the equivalent norm) can be regarded as the Besov-type space associated with uniform decomposition on the frequency domain. Another important function space that is closely related to the modulation space (see Lemma 2.6) is the Wiener amalgam space
$M^{p,q}_s$
(see [Reference Triebel18] for the equivalent norm) can be regarded as the Besov-type space associated with uniform decomposition on the frequency domain. Another important function space that is closely related to the modulation space (see Lemma 2.6) is the Wiener amalgam space
![]() $W^{p,q}_s$
(see §2.1). This space can be regarded as the Triebel-type space associated with uniform decomposition (see [Reference Triebel18] for the equivalent norm).
$W^{p,q}_s$
(see §2.1). This space can be regarded as the Triebel-type space associated with uniform decomposition (see [Reference Triebel18] for the equivalent norm).
Due to the boundedness in (1.2) and the fact that both modulation and Wiener amalgam space are defined based on the uniform decomposition, an interesting question is to establish the corresponding boundedness on
![]() $W^{p,q}_s$
of Schrödinger propagator. For this direction, Cunanan and Sugimoto [Reference Cunanan and Sugimoto5, Th. 1.1] proved the boundedness for
$W^{p,q}_s$
of Schrödinger propagator. For this direction, Cunanan and Sugimoto [Reference Cunanan and Sugimoto5, Th. 1.1] proved the boundedness for ![]() ,
,
![]() $s> d|1/p-1/q|$
. Conversely, Cordero and Nicola [Reference Cordero and Nicola4, Prop. 6.1] found some necessary conditions for this boundedness. Finally, a complete characterization was established by Kato and Tomita as follows.
$s> d|1/p-1/q|$
. Conversely, Cordero and Nicola [Reference Cordero and Nicola4, Prop. 6.1] found some necessary conditions for this boundedness. Finally, a complete characterization was established by Kato and Tomita as follows.
Theorem A [Reference Kato and Tomita16, Th. 1.1].
Suppose ![]() . Then
. Then
![]() $e^{i\Delta }: W^{p,q}_{1\otimes v_s}\rightarrow W^{p,q}$
is bounded if and only if
$e^{i\Delta }: W^{p,q}_{1\otimes v_s}\rightarrow W^{p,q}$
is bounded if and only if
![]() $s\geq d|1/p-1/q|$
with the strict inequality when
$s\geq d|1/p-1/q|$
with the strict inequality when
![]() $p\neq q$
.
$p\neq q$
.
Here, we write the power weights
![]() $v_s(\xi ):=(1+|\xi |^2)^{\frac {s}{2}}$
. From this theorem, one can find that the Schrödinger propagator is unbounded on
$v_s(\xi ):=(1+|\xi |^2)^{\frac {s}{2}}$
. From this theorem, one can find that the Schrödinger propagator is unbounded on
![]() $W^{p,q}_s$
for
$W^{p,q}_s$
for
![]() $p\neq q$
. This is quite different from the case on modulation spaces. We also refer to [Reference Guo and Zhao13] for the sharp estimate on
$p\neq q$
. This is quite different from the case on modulation spaces. We also refer to [Reference Guo and Zhao13] for the sharp estimate on
![]() $W^{p,q}_s$
of a class of unimodular Fourier multipliers. In fact, because of the weaker separation property of Triebel-type spaces, the behaviors of
$W^{p,q}_s$
of a class of unimodular Fourier multipliers. In fact, because of the weaker separation property of Triebel-type spaces, the behaviors of
![]() $e^{i\Delta }$
on
$e^{i\Delta }$
on
![]() $W^{p,q}_s$
are more difficult to study than those on modulation space. For instance, the boundedness
$W^{p,q}_s$
are more difficult to study than those on modulation space. For instance, the boundedness
![]() $e^{i\Delta }: M^{p_1, q_1}_{s}\rightarrow M^{p_2, q_2}$
of full range
$e^{i\Delta }: M^{p_1, q_1}_{s}\rightarrow M^{p_2, q_2}$
of full range
![]() $p_i, q_i\in (0,\infty ]$
has been established in [Reference Zhao, Chen, Fan and Guo22]. However, the corresponding boundedness result on Wiener amalgam space of full range is still unknown. The main goal of this paper is to fill this gap. To achieve this goal, our strategy is to first establish an equivalent characterization for the case of general weight. To avoid the fact that
$p_i, q_i\in (0,\infty ]$
has been established in [Reference Zhao, Chen, Fan and Guo22]. However, the corresponding boundedness result on Wiener amalgam space of full range is still unknown. The main goal of this paper is to fill this gap. To achieve this goal, our strategy is to first establish an equivalent characterization for the case of general weight. To avoid the fact that
![]() $\mathcal {S}({{\mathbb {R}}^d})$
is not dense in some endpoint spaces, such as the case
$\mathcal {S}({{\mathbb {R}}^d})$
is not dense in some endpoint spaces, such as the case
![]() $p=\infty $
or
$p=\infty $
or
![]() $q=\infty $
, we only consider the action of
$q=\infty $
, we only consider the action of
![]() $e^{i\Delta }$
on Schwartz function spaces. For the sake of simplicity, we use the statement “
$e^{i\Delta }$
on Schwartz function spaces. For the sake of simplicity, we use the statement “
![]() $e^{i\Delta }: W^{p_1,q_1}_{m}\rightarrow W^{p_2,q_2}$
” or
$e^{i\Delta }: W^{p_1,q_1}_{m}\rightarrow W^{p_2,q_2}$
” or
![]() $e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_{m},W^{p_2,q_2})$
to express the meaning that
$e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_{m},W^{p_2,q_2})$
to express the meaning that
Here, we use m to denote the weight function belonging to the class
![]() $\mathscr {P}({{{\mathbb R}}^{2d}})$
(see §2.1 for the precise definition). We write the dilation operator
$\mathscr {P}({{{\mathbb R}}^{2d}})$
(see §2.1 for the precise definition). We write the dilation operator ![]() . For a sequence
. For a sequence
![]() $\vec {a}=\{a_{k,n}\}$
, denote by
$\vec {a}=\{a_{k,n}\}$
, denote by
![]() $(\mathcal {T}\vec {a})_{k,n}=a_{k-n,n}$
the coordinate transformation of
$(\mathcal {T}\vec {a})_{k,n}=a_{k-n,n}$
the coordinate transformation of
![]() $\vec {a}$
. Our first theorem gives an equivalent characterization of boundedness.
$\vec {a}$
. Our first theorem gives an equivalent characterization of boundedness.
Theorem 1.1 (Equivalent characterization).
Let
![]() $p_i, q_i\in (0,\infty ]$
for
$p_i, q_i\in (0,\infty ]$
for
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. We have the following equivalent relation:
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. We have the following equivalent relation:
Thanks to the above equivalent relation, one can turn to studying the corresponding discrete inequality without having to consider the Schrödinger propagator directly. Our second theorem is a sharp exponents characterization for the case of
![]() $m=1\otimes v_s$
. It is known that the boundedness
$m=1\otimes v_s$
. It is known that the boundedness
![]() $e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_{1\otimes v_s}({{\mathbb {R}}^d}),W^{p_2,q_2}({{\mathbb {R}}^d}))$
is the most interesting case, especially in the crossing field of harmonic analysis and PDEs.
$e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_{1\otimes v_s}({{\mathbb {R}}^d}),W^{p_2,q_2}({{\mathbb {R}}^d}))$
is the most interesting case, especially in the crossing field of harmonic analysis and PDEs.
Theorem 1.2 (Sharp exponents characterization).
Let
![]() $s\in \mathbb {R}$
,
$s\in \mathbb {R}$
,
![]() $p_i, q_i\in (0,\infty ]$
for
$p_i, q_i\in (0,\infty ]$
for
![]() $i=1,2$
. Denote
$i=1,2$
. Denote
![]() $A=d(1/p_2-1/q_1)$
and
$A=d(1/p_2-1/q_1)$
and
![]() $B=d(1/q_2-1/p_1)$
. The boundedness
$B=d(1/q_2-1/p_1)$
. The boundedness
holds if and only if ![]() and
and
with the strict inequality if one of the following cases happens:
-
1.
 $A>0\geq B$
;
$A>0\geq B$
; -
2.
 $B>0\geq A$
;
$B>0\geq A$
; -
3.
 $A, B>0$
,
$A, B>0$
,
 $p_1=p_2$
.
$p_1=p_2$
.
Using this theorem, one can conclude directly the following boundedness of Schrödinger propagator on Wiener amalgam spaces without potential loss.
Corollary 1.3.
![]() $e^{i\Delta } \in \mathcal {L}(W^{p_1,q_1}({{\mathbb {R}}^d}),W^{p_2,q_2}({{\mathbb {R}}^d}))$
holds if and only if
$e^{i\Delta } \in \mathcal {L}(W^{p_1,q_1}({{\mathbb {R}}^d}),W^{p_2,q_2}({{\mathbb {R}}^d}))$
holds if and only if
Remark 1.4. Some remarks about our main theorems are listed as follows:
-
1. The proof of Theorem 1.1 is based on the Gabor analysis of Wiener amalgam space and the magic formula in Lemma 3.1 associated with Schrödinger propagator and the time–frequency shift. We point out that this formula was also used in [Reference Kato, Kobayashi and Ito15] for giving some conservation quantity associated with Schrödinger propagator.
-
2. Theorem 1.2 is an essential extension of Theorem A in [Reference Kato and Tomita16]. In our theorem of full range, more endpoint cases create new difficulties. The equivalent characterization in Theorem 1.1 allows us to see the nature more clearly and solve it.
-
3. All the conclusions in Theorems 1.1 and 1.2 can be extended to the fixed time Schrödinger propagator
 $e^{it_0\Delta }$
for any fixed
$e^{it_0\Delta }$
for any fixed
 $t_0\in \mathbb {R}$
.
$t_0\in \mathbb {R}$
. -
4. The method of this paper is also applicable in the study of the following boundedness:
 $$\begin{align*}e^{i\Delta} \in \mathcal {L}(X_1, X_2), \text{ with }X_j=W^{p_j,q_j}_{m_j} \text{ or } M^{p_j,q_j}_{m_j}, j=1,2. \end{align*}$$
$$\begin{align*}e^{i\Delta} \in \mathcal {L}(X_1, X_2), \text{ with }X_j=W^{p_j,q_j}_{m_j} \text{ or } M^{p_j,q_j}_{m_j}, j=1,2. \end{align*}$$
-
5. Although the magic formula in Lemma 3.1 seems to hold only for very special unimodular Fourier multipliers, the similar equivalent characterizations as in Theorem 1.1 of general unimodular Fourier multipliers are still expected to be valid with appropriate modification. However, the exponents characterizations as in Theorem 1.2 should be much more difficult for more general unimodular Fourier multipliers.
The rest of this paper is organized as follows. In §2, we first introduce some basic definitions and properties of the function spaces used throughout this paper. We also prepare some useful conclusions of the Gabor analysis on Wiener amalgam space. Section 3 is devoted to the equivalent characterization of the boundedness
![]() $e^{i\Delta }: W^{p_1,q_1}_m\rightarrow W^{p_2,q_2}$
. As mentioned above, the key tools are the Gabor analysis and the magic formula of Schrödinger propagator. The sharp exponents characterization is proved in §4. In some critical case, the boundedness of Schrödinger propagator is found to be equivalent to the boundedness of fractional integral operators.
$e^{i\Delta }: W^{p_1,q_1}_m\rightarrow W^{p_2,q_2}$
. As mentioned above, the key tools are the Gabor analysis and the magic formula of Schrödinger propagator. The sharp exponents characterization is proved in §4. In some critical case, the boundedness of Schrödinger propagator is found to be equivalent to the boundedness of fractional integral operators.
Throughout the context, we adopt the notation ![]() to denote the statement that
to denote the statement that ![]() , and the notation
, and the notation
![]() $X\sim Y$
means the statement
$X\sim Y$
means the statement ![]() , where the positive constants C might be different from line to line. Let
, where the positive constants C might be different from line to line. Let
![]() $\mathcal {S}:= \mathcal {S}(\mathbb {R}^{d})$
be the Schwartz space, and let
$\mathcal {S}:= \mathcal {S}(\mathbb {R}^{d})$
be the Schwartz space, and let
![]() $\mathcal {S}':=\mathcal {S}'(\mathbb {R}^{d})$
be the space of tempered distributions. The Fourier transform
$\mathcal {S}':=\mathcal {S}'(\mathbb {R}^{d})$
be the space of tempered distributions. The Fourier transform
![]() $\mathscr {F}f$
and the inverse Fourier transform
$\mathscr {F}f$
and the inverse Fourier transform
![]() $\mathscr {F}^{-1}f$
of
$\mathscr {F}^{-1}f$
of
![]() $f\in \mathcal {S}(\mathbb {R}^{n})$
are defined by
$f\in \mathcal {S}(\mathbb {R}^{n})$
are defined by
 $$ \begin{align*}\mathscr{F}f(\xi)=\hat{f}(\xi)=\int_{\mathbb{R}^{d}}f(x)e^{-2\pi ix\cdot \xi}dx, \hspace{2mm} \mathscr{F}^{-1}f(x)=\check{f}(x)=\int_{\mathbb{R}^{d}}f(\xi)e^{2\pi ix\cdot \xi}d\xi. \end{align*} $$
$$ \begin{align*}\mathscr{F}f(\xi)=\hat{f}(\xi)=\int_{\mathbb{R}^{d}}f(x)e^{-2\pi ix\cdot \xi}dx, \hspace{2mm} \mathscr{F}^{-1}f(x)=\check{f}(x)=\int_{\mathbb{R}^{d}}f(\xi)e^{2\pi ix\cdot \xi}d\xi. \end{align*} $$
2. Preliminaries
2.1. Function spaces
In order to introduce the function spaces, we first recall some definitions of weight. Recall that a weight is a positive and locally integral function on
![]() ${{{\mathbb R}}^{2d}}$
. A weight function m is called v-moderate if there exists another weight function v such that
${{{\mathbb R}}^{2d}}$
. A weight function m is called v-moderate if there exists another weight function v such that
where v belongs to the class of submultiplicative weight, that is, v satisfies
Moreover, in this paper, we assume that v has at most polynomial growth. If the associated weight v is implicit, we call that m is moderate and use the notation
![]() $\mathscr {P}({{{\mathbb R}}^{2d}})$
to denote the cone of all wights which are moderate in
$\mathscr {P}({{{\mathbb R}}^{2d}})$
to denote the cone of all wights which are moderate in
![]() ${{{\mathbb R}}^{2d}}$
. We also assume that every
${{{\mathbb R}}^{2d}}$
. We also assume that every
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
is continuous since there exists a continuous weight
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
is continuous since there exists a continuous weight
![]() $m_1$
such that
$m_1$
such that
![]() $m\sim m_1$
. We refer to [Reference Feichtinger6] for the origin of the v-moderate weights. See also [Reference Heil, Krishna, Radha and Thangavelu14] for more properties of these weights.
$m\sim m_1$
. We refer to [Reference Feichtinger6] for the origin of the v-moderate weights. See also [Reference Heil, Krishna, Radha and Thangavelu14] for more properties of these weights.
Definition 2.1 (Continuous mixed-norm spaces).
Let
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
,
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
,
![]() $p,q\in (0,\infty ]$
. The weighted mixed-norm space
$p,q\in (0,\infty ]$
. The weighted mixed-norm space
![]() $L^{p,q}_m({{{\mathbb R}}^{2d}})$
consists of all Lebesgue measurable functions on
$L^{p,q}_m({{{\mathbb R}}^{2d}})$
consists of all Lebesgue measurable functions on
![]() ${{{\mathbb R}}^{2d}}$
such that the (quasi-)norm
${{{\mathbb R}}^{2d}}$
such that the (quasi-)norm

is finite, with the usual modification when
![]() $p=\infty $
or
$p=\infty $
or
![]() $q=\infty $
. We also use the notation
$q=\infty $
. We also use the notation

Then the mixed-norm space
![]() $L^{(p,q)}_m({{{\mathbb R}}^{2d}})$
can be defined by the similar way as above.
$L^{(p,q)}_m({{{\mathbb R}}^{2d}})$
can be defined by the similar way as above.
In order to introduce the definitions of modulation and Wiener amalgam spaces, we recall some definitions and notations in time–frequency analysis. For
![]() $x,\xi \in \mathbb {R}^d$
, the translation operator
$x,\xi \in \mathbb {R}^d$
, the translation operator
![]() $T_x$
and the modulation operator
$T_x$
and the modulation operator
![]() $M_{\xi }$
are given by
$M_{\xi }$
are given by
For
![]() $z:=(x, \xi )$
, we also use the notation
$z:=(x, \xi )$
, we also use the notation
![]() $\pi (z):=M_{\xi }T_x$
, which is also known as the time–frequency shift on the phase plane.
$\pi (z):=M_{\xi }T_x$
, which is also known as the time–frequency shift on the phase plane.
Definition 2.2. Let
![]() $g\in \mathcal {S}(\mathbb {R}^d)\setminus \{0\}$
, the short-time Fourier transform (STFT) of
$g\in \mathcal {S}(\mathbb {R}^d)\setminus \{0\}$
, the short-time Fourier transform (STFT) of
![]() $f\in \mathcal {S}'(\mathbb {R}^d)$
with respect to the window g is defined by
$f\in \mathcal {S}'(\mathbb {R}^d)$
with respect to the window g is defined by

where the integral makes sense for nice function f.
The so-called fundamental identity of time–frequency analysis is as follows:
It can be observed that the STFT of a distribution f takes both the decay and smooth properties into account. The modulation space can be regarded as a collection of functions sharing the same decay and smooth properties. Now, we recall the definition of modulation space.
Definition 2.3 (Modulation space).
Let ![]() ,
,
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. Given a nonzero window function
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. Given a nonzero window function
![]() $\phi \in \mathcal {S}({{\mathbb {R}}^d})$
, the (weighted) modulation space
$\phi \in \mathcal {S}({{\mathbb {R}}^d})$
, the (weighted) modulation space
![]() $M^{p,q}_m({{\mathbb {R}}^d})$
consists of all
$M^{p,q}_m({{\mathbb {R}}^d})$
consists of all
![]() $f\in \mathcal {S}'({{\mathbb {R}}^d})$
such that the (quasi-)norm
$f\in \mathcal {S}'({{\mathbb {R}}^d})$
such that the (quasi-)norm

is finite. If
![]() $m\equiv 1$
, we write
$m\equiv 1$
, we write
![]() $M^{p,q}$
for short. We also write
$M^{p,q}$
for short. We also write
![]() $M^{p,q}_s$
for the case
$M^{p,q}_s$
for the case
![]() $m=1\otimes v_s$
.
$m=1\otimes v_s$
.
Recall that the above definition of
![]() $M^{p,q}_m$
is independent of the choice of window function
$M^{p,q}_m$
is independent of the choice of window function
![]() $\phi $
. We refer the readers to [Reference Gröchenig9] for the case
$\phi $
. We refer the readers to [Reference Gröchenig9] for the case ![]() and to [Reference Galperin and Samarah8, Th. 3.1] for full range
and to [Reference Galperin and Samarah8, Th. 3.1] for full range
![]() $(p,q)\in (0,\infty ]^{2}$
. More precisely, a class of admissible windows denoted by
$(p,q)\in (0,\infty ]^{2}$
. More precisely, a class of admissible windows denoted by
![]() $\mathfrak {M}^{p,q}_v$
was found in [Reference Galperin and Samarah8] such that every window function
$\mathfrak {M}^{p,q}_v$
was found in [Reference Galperin and Samarah8] such that every window function
![]() $g\in \mathfrak {M}^{p,q}_v$
yields the equivalent quasi-norm on
$g\in \mathfrak {M}^{p,q}_v$
yields the equivalent quasi-norm on
![]() ${M^{p,q}_m}$
.
${M^{p,q}_m}$
.
Definition 2.4 (The space of admissible windows).
Let ![]() ,
,
![]() $r=\min \{1,p\}$
, and
$r=\min \{1,p\}$
, and
![]() $s=\min \{1, p, q\}$
. Let m be v-moderate. For
$s=\min \{1, p, q\}$
. Let m be v-moderate. For
![]() $r_1, s_1>0$
, denote
$r_1, s_1>0$
, denote
Then
![]() $\mathfrak {M}_v^{p,q}$
the admissible windows for the modulation space
$\mathfrak {M}_v^{p,q}$
the admissible windows for the modulation space
![]() $M_m^{p,q}$
can be defined as
$M_m^{p,q}$
can be defined as

Next, we recall the definition of the
![]() $W^{p,q}_m$
space.
$W^{p,q}_m$
space.
Definition 2.5 (Wiener amalgam space).
Let ![]() ,
,
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. Given a nonzero window function
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. Given a nonzero window function
![]() $\phi \in \mathcal {S}({{\mathbb {R}}^d})$
, the (weighted) Wiener amalgam space
$\phi \in \mathcal {S}({{\mathbb {R}}^d})$
, the (weighted) Wiener amalgam space
![]() $W^{p,q}_m(\mathbb {R}^d)$
consists of all tempered distributions
$W^{p,q}_m(\mathbb {R}^d)$
consists of all tempered distributions
![]() $f\in \mathcal {S}'(\mathbb {R}^d)$
such that
$f\in \mathcal {S}'(\mathbb {R}^d)$
such that

is finite. We write briefly
![]() $W^{p,q}$
for the case
$W^{p,q}$
for the case
![]() $m(x,\xi )\equiv 1$
. We also use the notation
$m(x,\xi )\equiv 1$
. We also use the notation
![]() $W^{p,q}_s$
for the case
$W^{p,q}_s$
for the case
![]() $m=1\otimes v_s$
.
$m=1\otimes v_s$
.
Recall that there is a close connection between modulation and Wiener amalgam spaces.
Lemma 2.6. Denote
![]() $\widetilde {m}(x,\xi ):=m(\xi ,-x)$
. We have
$\widetilde {m}(x,\xi ):=m(\xi ,-x)$
. We have
![]() $W^{p,q}_m=\mathscr {F} M^{q,p}_{\widetilde {m}}$
. More precisely, the following relation is valid:
$W^{p,q}_m=\mathscr {F} M^{q,p}_{\widetilde {m}}$
. More precisely, the following relation is valid:
Due to the above relation, many conclusions can be automatically converted from modulation spaces to Wiener amalgam spaces. For instance, the definition of
![]() $W^{p,q}_m$
is independent of the window
$W^{p,q}_m$
is independent of the window
![]() $g\in \mathscr {F}\mathfrak {M}_{\widetilde {v}}^{q,p}$
, where
$g\in \mathscr {F}\mathfrak {M}_{\widetilde {v}}^{q,p}$
, where
![]() $\widetilde {v}(x,\xi ):=v(\xi ,-x)$
.
$\widetilde {v}(x,\xi ):=v(\xi ,-x)$
.
2.2. Gabor analysis on modulation and Wiener amalgam spaces
In this subsection, we recall an important time–frequency tool on modulation and Wiener amalgam spaces. In fact, the functions or distributions in modulation and Wiener amalgam spaces can be characterized by the summability and decay properties of their Gabor coefficients. We first list some important operators with their basic properties.
Definition 2.7. Assume that
![]() $g,\gamma \in L^2(\mathbb {R}^d)$
,
$g,\gamma \in L^2(\mathbb {R}^d)$
,
![]() $\alpha ,\beta>0$
, and
$\alpha ,\beta>0$
, and
![]() $\Gamma =\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$
. The coefficient operator or analysis operator
$\Gamma =\alpha \mathbb {Z}^d\times \beta \mathbb {Z}^d$
. The coefficient operator or analysis operator
![]() $C^{\alpha ,\beta }_g$
is defined by
$C^{\alpha ,\beta }_g$
is defined by
The synthesis operator or reconstruction operator
![]() $D^{\alpha ,\beta }_{\gamma }$
is defined by
$D^{\alpha ,\beta }_{\gamma }$
is defined by
 $$ \begin{align*} D^{\alpha,\beta}_{\gamma}\vec{c}=\sum_{k\in \mathbb{Z}^d}\sum_{n\in \mathbb{Z}^d} c_{k,n}M_{\beta n}T_{\alpha k}\gamma. \end{align*} $$
$$ \begin{align*} D^{\alpha,\beta}_{\gamma}\vec{c}=\sum_{k\in \mathbb{Z}^d}\sum_{n\in \mathbb{Z}^d} c_{k,n}M_{\beta n}T_{\alpha k}\gamma. \end{align*} $$
The Gabor frame operator
![]() $S^{\alpha ,\beta }_{g,\gamma }$
is defined by
$S^{\alpha ,\beta }_{g,\gamma }$
is defined by

We also use
![]() $C_g$
,
$C_g$
,
![]() $D_{\gamma }$
, and
$D_{\gamma }$
, and
![]() $S_{g,\gamma }$
for short, if the parameters
$S_{g,\gamma }$
for short, if the parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are implicit.
$\beta $
are implicit.
We remark that the definitions of
![]() $C_g$
and
$C_g$
and
![]() $D_{\gamma }$
can be extended if the window functions g and
$D_{\gamma }$
can be extended if the window functions g and
![]() $\gamma $
are taken suitably. Next, we give the definitions of discrete mixed-norm spaces.
$\gamma $
are taken suitably. Next, we give the definitions of discrete mixed-norm spaces.
Definition 2.8 (Discrete mixed-norm spaces).
Let ![]() ,
,
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. The space
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. The space
![]() $l^{p,q}_m({{\mathbb {Z}}^{2d}})$
consists of all sequences
$l^{p,q}_m({{\mathbb {Z}}^{2d}})$
consists of all sequences
![]() $\vec {a}=\{a_{k,n}\}_{k,n\in {{\mathbb {Z}}^d}}$
for which the (quasi-)norm
$\vec {a}=\{a_{k,n}\}_{k,n\in {{\mathbb {Z}}^d}}$
for which the (quasi-)norm

is finite, with the usual modification when
![]() $p=\infty $
or
$p=\infty $
or
![]() $q=\infty $
. We also use the notation
$q=\infty $
. We also use the notation

Then the mixed-norm space
![]() $l^{(p,q)}_m({{\mathbb {Z}}^{2d}})$
can be defined by the similar way. For a continuous function F on
$l^{(p,q)}_m({{\mathbb {Z}}^{2d}})$
can be defined by the similar way. For a continuous function F on
![]() ${{{\mathbb R}}^{2d}}$
, we define
${{{\mathbb R}}^{2d}}$
, we define
Based on the admissible window class mentioned above, we recall the boundedness of
![]() $C_g$
and
$C_g$
and
![]() $D_{g}$
, which works on the full range
$D_{g}$
, which works on the full range
![]() $p,q\in (0,\infty ]$
(see [Reference Galperin and Samarah8] for more details).
$p,q\in (0,\infty ]$
(see [Reference Galperin and Samarah8] for more details).
Lemma 2.9 (See Theorems 3.5 and 3.6 in [Reference Galperin and Samarah8]).
Assume that m is v-moderate,
![]() $p,q\in (0,\infty ]$
, and g belongs to the subclass
$p,q\in (0,\infty ]$
, and g belongs to the subclass
![]() $M^{p_1}_{\omega _{r_1,s_1}}$
of
$M^{p_1}_{\omega _{r_1,s_1}}$
of
![]() $\mathfrak {M}^{p,q}_v$
. For all lattice constants
$\mathfrak {M}^{p,q}_v$
. For all lattice constants
![]() $\alpha , \beta>0$
, we have
$\alpha , \beta>0$
, we have
and
independently of
![]() $p,q,m$
.
$p,q,m$
.
Now, we recall the Gabor characterization of modulation space in [Reference Galperin and Samarah8, Th. 3.7].
Lemma 2.10 (Gabor characterization of
 ${M^{p,q}_m}$
with
${M^{p,q}_m}$
with  ).
).
Assume that m is v-moderate on
![]() $\mathbb {R}^{2d}$
,
$\mathbb {R}^{2d}$
,
![]() $p,q\in (0,\infty ]$
,
$p,q\in (0,\infty ]$
,
![]() $g,\gamma \in \mathfrak {M}^{p,q}_v$
, and that the Gabor frame operator
$g,\gamma \in \mathfrak {M}^{p,q}_v$
, and that the Gabor frame operator
![]() $S_{g,\gamma }=D_{\gamma }C_g=I$
on
$S_{g,\gamma }=D_{\gamma }C_g=I$
on
![]() $L^2(\mathbb {R}^d)$
. Then
$L^2(\mathbb {R}^d)$
. Then

with unconditional convergence in
![]() $M^{p,q}_m$
if
$M^{p,q}_m$
if
![]() $p,q<\infty $
, and with weak-star convergence in
$p,q<\infty $
, and with weak-star convergence in
![]() $M^{\infty }_{1/v}$
otherwise. Furthermore, there are constants
$M^{\infty }_{1/v}$
otherwise. Furthermore, there are constants
![]() $A,B>0$
such that for all
$A,B>0$
such that for all
![]() $f\in M^{p,q}_m$
,
$f\in M^{p,q}_m$
,
Next, we list the corresponding results on Wiener amalgam spaces, which can be verified by using Lemmas 2.9 and 2.10 and the fundamental identity (2.1) directly. We omit the proof here.
Lemma 2.11. Assume that m is v-moderate,
![]() $p,q\in (0,\infty ]$
, and g belongs to the subclass
$p,q\in (0,\infty ]$
, and g belongs to the subclass
![]() $\mathscr {F} M^{p_1}_{\omega _{r_1,s_1}}$
of
$\mathscr {F} M^{p_1}_{\omega _{r_1,s_1}}$
of
![]() $\mathscr {F} \mathfrak {M}^{q,p}_{\widetilde {v}}$
, where
$\mathscr {F} \mathfrak {M}^{q,p}_{\widetilde {v}}$
, where
![]() $\widetilde {v}(x,\xi ):=v(\xi ,-x)$
. For all lattice constants
$\widetilde {v}(x,\xi ):=v(\xi ,-x)$
. For all lattice constants
![]() $\alpha , \beta>0$
, we have
$\alpha , \beta>0$
, we have
and
independently of
![]() $p,q,m$
.
$p,q,m$
.
Lemma 2.12 (Gabor frames for Wiener spaces
 $W^{p,q}_m$
with
$W^{p,q}_m$
with  ).
).
Assume that m is v-moderate on
![]() $\mathbb {R}^{2d}$
,
$\mathbb {R}^{2d}$
,
![]() $p,q\in (0,\infty ]$
,
$p,q\in (0,\infty ]$
,
![]() $g, \gamma \in \mathscr {F}\mathfrak {M}^{q,p}_{\widetilde {v}}$
with
$g, \gamma \in \mathscr {F}\mathfrak {M}^{q,p}_{\widetilde {v}}$
with
![]() $\widetilde {v}(x,\xi ):=v(\xi ,-x)$
, and that the Gabor frame operator
$\widetilde {v}(x,\xi ):=v(\xi ,-x)$
, and that the Gabor frame operator
![]() $S_{g,\gamma }=D_{\gamma }C_g=I$
on
$S_{g,\gamma }=D_{\gamma }C_g=I$
on
![]() $L^2(\mathbb {R}^d)$
. Then
$L^2(\mathbb {R}^d)$
. Then

with unconditional convergence in
![]() $W^{p,q}_m$
if
$W^{p,q}_m$
if
![]() $p,q<\infty $
, and with weak-star convergence in
$p,q<\infty $
, and with weak-star convergence in
![]() $W^{\infty }_{1/v}$
otherwise. Furthermore, there are constants
$W^{\infty }_{1/v}$
otherwise. Furthermore, there are constants
![]() $A,B>0$
such that for all
$A,B>0$
such that for all
![]() $f\in W^{p,q}_m$
,
$f\in W^{p,q}_m$
,
The following well-known theorem provides a way to find the Gabor frame of
![]() $L^2(\mathbb {R}^d)$
. Recall that
$L^2(\mathbb {R}^d)$
. Recall that
![]() $\|g\|_{W(L^{\infty },L^{1})(\mathbb {R}^d)}=\sum _{n\in \mathbb {Z}^d}\|g\chi _{Q+n}\|_{L^{\infty }}$
with
$\|g\|_{W(L^{\infty },L^{1})(\mathbb {R}^d)}=\sum _{n\in \mathbb {Z}^d}\|g\chi _{Q+n}\|_{L^{\infty }}$
with
![]() $Q=[0,1]^d$
.
$Q=[0,1]^d$
.
Lemma 2.13 (Walnut [Reference Walnut19]).
Suppose that
![]() $g\in W(L^{\infty },L^{1})(\mathbb {R}^d)$
satisfies
$g\in W(L^{\infty },L^{1})(\mathbb {R}^d)$
satisfies

for constants
![]() $A,B\in (0,\infty )$
. Then there exists a constant
$A,B\in (0,\infty )$
. Then there exists a constant
![]() $\beta _0$
depending on
$\beta _0$
depending on
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {G}(g,\alpha ,\beta ):= \{T_{\alpha k}M_{\beta n}g\}_{k,n\in \mathbb {Z}^d}$
is a Gabor frame of
$\mathcal {G}(g,\alpha ,\beta ):= \{T_{\alpha k}M_{\beta n}g\}_{k,n\in \mathbb {Z}^d}$
is a Gabor frame of
![]() $L^2(\mathbb {R}^d)$
for all
$L^2(\mathbb {R}^d)$
for all ![]() .
.
In order to find the dual window in a suitable function space, we recall the following conclusion.
Lemma 2.14 (See Theorem 4.2 in [Reference Gröchenig and Leinert10]).
Assume that
![]() $g\in M^1_v({{\mathbb {R}}^d})$
and that
$g\in M^1_v({{\mathbb {R}}^d})$
and that
![]() $\{T_{\alpha k}M_{\beta n}g\}_{k,n\in {{\mathbb {Z}}^d}}$
is a Gabor frame for
$\{T_{\alpha k}M_{\beta n}g\}_{k,n\in {{\mathbb {Z}}^d}}$
is a Gabor frame for
![]() $L^2({{\mathbb {R}}^d})$
. Then the Gabor frame operator
$L^2({{\mathbb {R}}^d})$
. Then the Gabor frame operator
![]() $S_{g,g}^{\alpha ,\beta }$
is invertible on
$S_{g,g}^{\alpha ,\beta }$
is invertible on
![]() $M^1_v({{\mathbb {R}}^d})$
. As a consequence,
$M^1_v({{\mathbb {R}}^d})$
. As a consequence,
![]() $S_{g,g}^{\alpha ,\beta }$
is invertible on all modulation spaces
$S_{g,g}^{\alpha ,\beta }$
is invertible on all modulation spaces
![]() $M^{p,q}_m({{\mathbb {R}}^d})$
for
$M^{p,q}_m({{\mathbb {R}}^d})$
for ![]() and
and
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
.
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
.
Based on the above lemmas, we give a lemma used in our proof of Theorem 1.1.
Lemma 2.15. Suppose that
![]() $p_i,q_i\in (0,\infty ]$
,
$p_i,q_i\in (0,\infty ]$
,
![]() $m_i\in \mathscr {P}({{\mathbb {R}}^d})$
,
$m_i\in \mathscr {P}({{\mathbb {R}}^d})$
,
![]() $i=1,2$
. For any
$i=1,2$
. For any
![]() $g_1, g_2\in \mathcal {S}({{\mathbb {R}}^d})\backslash \{0\}$
, there exists a constant
$g_1, g_2\in \mathcal {S}({{\mathbb {R}}^d})\backslash \{0\}$
, there exists a constant
![]() $N\in \mathbb {N}$
such that for all
$N\in \mathbb {N}$
such that for all
![]() $f\in \mathcal {S}({{\mathbb {R}}^d})$
,
$f\in \mathcal {S}({{\mathbb {R}}^d})$
,
Proof. For nonzero Schwartz functions
![]() $g_1$
and
$g_1$
and
![]() $g_2$
, there exists a constant
$g_2$
, there exists a constant
![]() $\alpha =1/\widetilde {N}$
with
$\alpha =1/\widetilde {N}$
with
![]() $\widetilde {N}\in \mathbb {N}$
such that
$\widetilde {N}\in \mathbb {N}$
such that

Using Lemma 2.13, one can find a constant
![]() $\beta =\alpha /L$
with
$\beta =\alpha /L$
with
![]() $L\in \mathbb {N}$
such that
$L\in \mathbb {N}$
such that
![]() $\mathcal {G}(g_i,\alpha ,\beta ):= \{T_{\alpha k}M_{\beta n}g_i\}_{k,n\in \mathbb {Z}^d}$
is a Gabor frame of
$\mathcal {G}(g_i,\alpha ,\beta ):= \{T_{\alpha k}M_{\beta n}g_i\}_{k,n\in \mathbb {Z}^d}$
is a Gabor frame of
![]() $L^2(\mathbb {R}^d)$
for
$L^2(\mathbb {R}^d)$
for
![]() $i=1,2$
, respectively. Denote by
$i=1,2$
, respectively. Denote by
![]() ${\gamma _i=(S_{g_i,g_i}^{\alpha ,\beta })^{-1}g_i}$
be the canonical dual window function of
${\gamma _i=(S_{g_i,g_i}^{\alpha ,\beta })^{-1}g_i}$
be the canonical dual window function of
![]() $g_i$
for
$g_i$
for
![]() $i=1,2$
. Using Lemma 2.14, we find that
$i=1,2$
. Using Lemma 2.14, we find that
![]() $\gamma _i\in M^1_{v_s\otimes v_s}$
for any sufficiently large
$\gamma _i\in M^1_{v_s\otimes v_s}$
for any sufficiently large
![]() $s>0$
. It follows that
$s>0$
. It follows that
![]() $\gamma _i\in \mathscr {F} M^1_{v_s\otimes v_s}\subset \mathscr {F}\mathfrak {M}^{q_i,p_i}_{\widetilde {v_i}}$
, where
$\gamma _i\in \mathscr {F} M^1_{v_s\otimes v_s}\subset \mathscr {F}\mathfrak {M}^{q_i,p_i}_{\widetilde {v_i}}$
, where
![]() $\widetilde {v_i}(x,\xi ):=v_i(\xi ,-x)$
,
$\widetilde {v_i}(x,\xi ):=v_i(\xi ,-x)$
,
![]() $i=1,2$
. We also have
$i=1,2$
. We also have
![]() $S_{g_i,\gamma _i}=D_{\gamma _i}C_{g_i}=I$
on
$S_{g_i,\gamma _i}=D_{\gamma _i}C_{g_i}=I$
on
![]() $L^2(\mathbb {R}^d)$
.
$L^2(\mathbb {R}^d)$
.
Using Lemma 2.12, one can find two constants
![]() $A,B>0$
such that for every
$A,B>0$
such that for every
![]() $f\in \mathcal {S}({{\mathbb {R}}^d})$
,
$f\in \mathcal {S}({{\mathbb {R}}^d})$
,
Denote
![]() $N=L\widetilde {N}$
. Note that
$N=L\widetilde {N}$
. Note that
![]() $\alpha {{\mathbb {Z}}^d}\times \beta {{\mathbb {Z}}^d} \subset \beta {{\mathbb {Z}}^d}\times \beta {{\mathbb {Z}}^d}={{\mathbb {Z}}^d}/N\times {{\mathbb {Z}}^d}/N$
. We obtain
$\alpha {{\mathbb {Z}}^d}\times \beta {{\mathbb {Z}}^d} \subset \beta {{\mathbb {Z}}^d}\times \beta {{\mathbb {Z}}^d}={{\mathbb {Z}}^d}/N\times {{\mathbb {Z}}^d}/N$
. We obtain
On the other hand, the sampling property (see Lemma 2.11) yields that

The desired conclusion follows by the above two estimates.
3. Characterization of boundedness of
 $e^{i\Delta }$
on Wiener amalgam spaces
$e^{i\Delta }$
on Wiener amalgam spaces
In this section, we give the proof of Theorem 1.1, showing that the boundedness
![]() ${e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_m,W^{p_2,q_2})}$
is equivalent to the corresponding boundedness on discrete mixed spaces of coordinate transformation
${e^{i\Delta }\in \mathcal {L}(W^{p_1,q_1}_m,W^{p_2,q_2})}$
is equivalent to the corresponding boundedness on discrete mixed spaces of coordinate transformation
![]() $\mathcal {T}$
. To achieve this goal, we first give a calculation of STFT associated with Schördinger operator. See also [Reference Kato, Kobayashi and Ito15].
$\mathcal {T}$
. To achieve this goal, we first give a calculation of STFT associated with Schördinger operator. See also [Reference Kato, Kobayashi and Ito15].
Lemma 3.1 (STFT of
 $e^{-i\pi |D|^2}$
).
$e^{-i\pi |D|^2}$
).
For
![]() $f\in \mathscr {S}'$
,
$f\in \mathscr {S}'$
,
![]() $\phi \in \mathscr {S}$
, we have
$\phi \in \mathscr {S}$
, we have
Proof. Note that
![]() $e^{-i\pi |D|^2}\phi \in \mathscr {S}$
. Using the foundation identity of time–frequency analysis, we find that
$e^{-i\pi |D|^2}\phi \in \mathscr {S}$
. Using the foundation identity of time–frequency analysis, we find that

For convenience in the proof of Theorem 1.1, we would like to use the boundedness of
![]() $e^{-i\pi |D|^2}$
rather than that of the standard Schrödinger propagator
$e^{-i\pi |D|^2}$
rather than that of the standard Schrödinger propagator
![]() $e^{i\Delta }$
. The following lemma gives the relationship between the boundedness of these two operators.
$e^{i\Delta }$
. The following lemma gives the relationship between the boundedness of these two operators.
Lemma 3.2 (Boundedness of
 $e^{-i\pi |D|^2}$
and
$e^{-i\pi |D|^2}$
and
 $e^{i\Delta }$
).
$e^{i\Delta }$
).
Let
![]() $p_i, q_i\in (0,\infty ]$
for
$p_i, q_i\in (0,\infty ]$
for
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. We have the following equivalent relation:
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. We have the following equivalent relation:
Proof. By using the scaling property of the Fourier transform and a direct calculation, we have
 $$ \begin{align*} e^{i\Delta}f &= \mathscr{F}^{-1}(e^{-4\pi i|\omega|^2}\hat{f}(\omega)) =\mathscr{F}^{-1}(e^{-i\pi|2\omega|^2}\hat{f}(\omega)) =2^d\mathscr{F}^{-1}(e^{-i\pi|2\omega|^2}\widehat{\mathcal {D}_{2}f}(2\omega)) \\ &= \mathcal {D}_{1/2}\mathscr{F}^{-1}(e^{-i\pi|\omega|^2}\widehat{\mathcal {D}_{2}f}(\omega)) =\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f. \end{align*} $$
$$ \begin{align*} e^{i\Delta}f &= \mathscr{F}^{-1}(e^{-4\pi i|\omega|^2}\hat{f}(\omega)) =\mathscr{F}^{-1}(e^{-i\pi|2\omega|^2}\hat{f}(\omega)) =2^d\mathscr{F}^{-1}(e^{-i\pi|2\omega|^2}\widehat{\mathcal {D}_{2}f}(2\omega)) \\ &= \mathcal {D}_{1/2}\mathscr{F}^{-1}(e^{-i\pi|\omega|^2}\widehat{\mathcal {D}_{2}f}(\omega)) =\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f. \end{align*} $$
Note that
For any
![]() $f\in \mathscr {S}$
, we have
$f\in \mathscr {S}$
, we have
 $$ \begin{align*} \|e^{i\Delta}f\|_{W^{p_2,q_2}} &= \|\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f\|_{W^{p_2,q_2}} = \|V_{\mathcal {D}_{1/2}\phi}(\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x,\omega)\|_{L^{(p_2,q_2)}} \\ &= 2^d\|V_{\phi}(e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x/2,2\omega)\|_{L^{(p_2,q_2)}} \sim \|V_{\phi}(e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x,\omega)\|_{L^{(p_2,q_2)}} \\ &= \|e^{-i\pi|D|^2}\mathcal {D}_{2}f\|_{W^{p_2,q_2}}. \end{align*} $$
$$ \begin{align*} \|e^{i\Delta}f\|_{W^{p_2,q_2}} &= \|\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f\|_{W^{p_2,q_2}} = \|V_{\mathcal {D}_{1/2}\phi}(\mathcal {D}_{1/2}e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x,\omega)\|_{L^{(p_2,q_2)}} \\ &= 2^d\|V_{\phi}(e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x/2,2\omega)\|_{L^{(p_2,q_2)}} \sim \|V_{\phi}(e^{-i\pi|D|^2}\mathcal {D}_{2}f)(x,\omega)\|_{L^{(p_2,q_2)}} \\ &= \|e^{-i\pi|D|^2}\mathcal {D}_{2}f\|_{W^{p_2,q_2}}. \end{align*} $$
On the other hand, we find
 $$ \begin{align*} \|f\|_{W^{p_1,q_1}_m} &= \|\mathcal {D}_{1/2}\mathcal {D}_2f\|_{W^{p_1,q_1}_m} = \|V_{\mathcal {D}_{1/2}\phi}(\mathcal {D}_{1/2}\mathcal {D}_2f)(x,\omega)m(x,\omega)\|_{L^{(p_1,q_1)}} \\ &= 2^d\|V_{\phi}(\mathcal {D}_2f)(x/2,2\omega)m(x,\omega)\|_{L^{(p_1,q_1)}} \sim \|V_{\phi}(\mathcal {D}_2f)(x,\omega)m(2x,\omega/2)\|_{L^{(p_1,q_1)}} \\ &=\|\mathcal {D}_2f\|_{W^{p_1,q_1}_{\mathcal {D}_{2,1/2}m}}. \end{align*} $$
$$ \begin{align*} \|f\|_{W^{p_1,q_1}_m} &= \|\mathcal {D}_{1/2}\mathcal {D}_2f\|_{W^{p_1,q_1}_m} = \|V_{\mathcal {D}_{1/2}\phi}(\mathcal {D}_{1/2}\mathcal {D}_2f)(x,\omega)m(x,\omega)\|_{L^{(p_1,q_1)}} \\ &= 2^d\|V_{\phi}(\mathcal {D}_2f)(x/2,2\omega)m(x,\omega)\|_{L^{(p_1,q_1)}} \sim \|V_{\phi}(\mathcal {D}_2f)(x,\omega)m(2x,\omega/2)\|_{L^{(p_1,q_1)}} \\ &=\|\mathcal {D}_2f\|_{W^{p_1,q_1}_{\mathcal {D}_{2,1/2}m}}. \end{align*} $$
From the above two estimates, for any
![]() $f\in \mathscr {S}$
, we have
$f\in \mathscr {S}$
, we have

Now, we turn to the characterization of the boundedness of
![]() $e^{-i\pi |D|^2}$
.
$e^{-i\pi |D|^2}$
.
Proposition 3.3 (Equivalent characterization for
 $e^{-i\pi |D|^2}$
).
$e^{-i\pi |D|^2}$
).
Let
![]() $p_i, q_i\in (0,\infty ]$
for
$p_i, q_i\in (0,\infty ]$
for
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. The following equivalent relation is valid:
$m\in \mathscr {P}({{{\mathbb R}}^{2d}})$
. The following equivalent relation is valid:
Proof. We first verify the “![]() ” direction. For this purpose, we choose a nonnegative function
” direction. For this purpose, we choose a nonnegative function
![]() $h\in \mathcal {S}({{\mathbb {R}}^d})\backslash \{0\}$
satisfying
$h\in \mathcal {S}({{\mathbb {R}}^d})\backslash \{0\}$
satisfying
![]() $\text {supp}\hat {h}\subset B(0,1/8)$
and
$\text {supp}\hat {h}\subset B(0,1/8)$
and
![]() $\|h\|_{L^2}=1$
. For any truncated (only finite nonzero terms) nonnegative sequence
$\|h\|_{L^2}=1$
. For any truncated (only finite nonzero terms) nonnegative sequence
![]() $\vec {a}=\{a_{k,n}\}_{(k,n)\in {{\mathbb {Z}}^{2d}}}$
, we define
$\vec {a}=\{a_{k,n}\}_{(k,n)\in {{\mathbb {Z}}^{2d}}}$
, we define
 $$ \begin{align*} f=D_{h}\vec{a}=\sum_{(k,n)\in {{\mathbb{Z}}^{2d}}}a_{k,n}\pi(k,n)h. \end{align*} $$
$$ \begin{align*} f=D_{h}\vec{a}=\sum_{(k,n)\in {{\mathbb{Z}}^{2d}}}a_{k,n}\pi(k,n)h. \end{align*} $$
By a direct calculation, we find that

Combining this with Lemma 2.11, the sampling property, and Lemma 3.1, we obtain
 $$ \begin{align*} \|e^{-i\pi|D|^2}f\|_{W^{p_2,q_2}} \gtrsim & \|V_{e^{-i\pi|D|^2 h}}(e^{-i\pi|D|^2}f)(k,n)\|_{l^{(p_2,q_2)}} \\ = & \|e^{-i\pi|n|^2} \cdot V_hf(k-n,n)\|_{l^{(p_2,q_2)}} \\ \geq& \|a_{k-n,n}\|_{l^{(p_2,q_2)}}=\|\mathcal {T} \vec{a}\||_{l^{(p_2,q_2)}({{\mathbb{Z}}^{2d}})}. \end{align*} $$
$$ \begin{align*} \|e^{-i\pi|D|^2}f\|_{W^{p_2,q_2}} \gtrsim & \|V_{e^{-i\pi|D|^2 h}}(e^{-i\pi|D|^2}f)(k,n)\|_{l^{(p_2,q_2)}} \\ = & \|e^{-i\pi|n|^2} \cdot V_hf(k-n,n)\|_{l^{(p_2,q_2)}} \\ \geq& \|a_{k-n,n}\|_{l^{(p_2,q_2)}}=\|\mathcal {T} \vec{a}\||_{l^{(p_2,q_2)}({{\mathbb{Z}}^{2d}})}. \end{align*} $$
On the other hand, by the boundedness of reconstruction operator (see Lemma 2.11), we obtain
The “![]() ” direction follows by the above two estimates.
” direction follows by the above two estimates.
Next, we turn to the “![]() ” direction. Using Lemma 2.15, we can find a constant
” direction. Using Lemma 2.15, we can find a constant
![]() $N\in \mathbb {N}$
such that for any
$N\in \mathbb {N}$
such that for any
![]() $f\in \mathcal {S}({{\mathbb {R}}^d})$
,
$f\in \mathcal {S}({{\mathbb {R}}^d})$
,

and

From this, in order to obtain the desired conclusion, we only need to verify the following inequality:

Using Lemma 3.1, this is equivalent to

For this constant
![]() $N\in \mathbb {N}$
, we construct a decomposition of
$N\in \mathbb {N}$
, we construct a decomposition of
![]() ${{\mathbb {Z}}^d}\times {{\mathbb {Z}}^d}$
by
${{\mathbb {Z}}^d}\times {{\mathbb {Z}}^d}$
by

where
![]() $ \Gamma _{j,l}:= \{(Nk+j,Nn+l), n,k\in \mathbb {Z}^d\}$
and
$ \Gamma _{j,l}:= \{(Nk+j,Nn+l), n,k\in \mathbb {Z}^d\}$
and ![]() Write
Write

Using the assumption
![]() $\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_m({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
, the last term above can be dominated by
$\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_m({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
, the last term above can be dominated by

where we use the fact that

We have now completed this proof.
4. Sharp exponents characterization of
 $e^{i\Delta }$
on Wiener amalgam spaces
$e^{i\Delta }$
on Wiener amalgam spaces
Thanks to the equivalent characterization in Theorem 1.1, we first consider the sharp exponents characterization for
![]() $\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
. The following lemmas play an important role in our proof.
$\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
. The following lemmas play an important role in our proof.
Lemma 4.1 (see Lemma 4.4 in [Reference Guo, Chen, Fan and Zhao11]).
![]() $l^{q,s}\subset l^p$
if and only if
$l^{q,s}\subset l^p$
if and only if
![]() $s\geq d(1/p-1/q)\vee 0$
with strict inequality if
$s\geq d(1/p-1/q)\vee 0$
with strict inequality if
![]() $1/p>1/q$
.
$1/p>1/q$
.
Lemma 4.2. Let ![]() ,
,
![]() $s\in {\mathbb R}$
. We have
$s\in {\mathbb R}$
. We have
![]() $\mathcal {T}\in \mathcal {L}(l^{(q,p)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}), l^{(p,q)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}))$
.
$\mathcal {T}\in \mathcal {L}(l^{(q,p)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}), l^{(p,q)}_{1\otimes v_s}({{\mathbb {Z}}^{2d}}))$
.
Proof. Write

Applying the Minkowski inequality, the last term can be dominated from above by

For the convenience of the readers, we introduce some notations used in the proof of Proposition 4.3. Denote
and let X be the set as follows:
Define the sets
![]() $X_j$
,
$X_j$
,
![]() $j=0,1,2,3$
, as
$j=0,1,2,3$
, as

Note that X is now the union of the mutually disjoint sets
![]() $X_j$
,
$X_j$
,
![]() $j=0,1,2,3$
. Denote
$j=0,1,2,3$
. Denote
![]() $Y_j=Y\cap X_j$
,
$Y_j=Y\cap X_j$
,
![]() $j=0,1,2,3$
. In the proof of Proposition 4.3, our strategy is to prove
$j=0,1,2,3$
. In the proof of Proposition 4.3, our strategy is to prove
![]() $Y\subset X$
first, and then to characterize the set
$Y\subset X$
first, and then to characterize the set
![]() $Y_j$
,
$Y_j$
,
![]() $j=0,1,2,3$
. Therefore, the desired set Y can be characterized by
$j=0,1,2,3$
. Therefore, the desired set Y can be characterized by
 $$ \begin{align*} Y=Y\cap X=Y\cap \bigg(\bigcup_{j=0}^3X_j\bigg)=\bigcup_{j=0}^3Y_j. \end{align*} $$
$$ \begin{align*} Y=Y\cap X=Y\cap \bigg(\bigcup_{j=0}^3X_j\bigg)=\bigcup_{j=0}^3Y_j. \end{align*} $$
Proposition 4.3 (Sharp exponents for
 $\mathcal {T}$
).
$\mathcal {T}$
).
Let
![]() $s\in \mathbb {R}$
,
$s\in \mathbb {R}$
,
![]() $p_i, q_i\in (0,\infty ]$
for
$p_i, q_i\in (0,\infty ]$
for
![]() $i=1,2$
. The boundedness
$i=1,2$
. The boundedness
holds if and only if ![]() and s satisfies the conditions in Theorem 1.2.
and s satisfies the conditions in Theorem 1.2.
Proof. Recall the definition of Y mentioned above. This proof is actually to characterize the set Y. It can be achieved by the following steps.
Step 1. The goal of this part is to verify that
![]() $Y\subset X$
. In fact, if we can verify the following claim:
$Y\subset X$
. In fact, if we can verify the following claim:

then the desired conclusion follows by Lemma 4.1. Now, we turn to the proof of this claim. If (4.1) holds, we have

The embedding relations
![]() $l^{p_1}\subset l^{p_2},\ \ l^{q_1}_{v_s}\subset l^{p_2},\ \ l^{p_1}_{v_s}\subset l^{q_2}$
follows by taking
$l^{p_1}\subset l^{p_2},\ \ l^{q_1}_{v_s}\subset l^{p_2},\ \ l^{p_1}_{v_s}\subset l^{q_2}$
follows by taking

in the inequality (4.3), respectively.
Moreover, for large constant N, take

Notice that
![]() $s\geq 0$
deduced by (4.2) and Lemma 4.1. One can verify that
$s\geq 0$
deduced by (4.2) and Lemma 4.1. One can verify that

Letting
![]() $N\rightarrow \infty $
, we obtain the desired conclusion
$N\rightarrow \infty $
, we obtain the desired conclusion
![]() $s\geq d(1/p_2-1/q_1+1/q_2-1/p_1)$
.
$s\geq d(1/p_2-1/q_1+1/q_2-1/p_1)$
.
Step 2. The goal of this part is to verify that
![]() $Y_0=Z_0$
, where
$Y_0=Z_0$
, where ![]() . It is obvious to see that
. It is obvious to see that
![]() $Z_0=X_0$
. To achieve this goal, we only need to verify that
$Z_0=X_0$
. To achieve this goal, we only need to verify that
![]() $Z_0\subset Y$
. In this case, we have
$Z_0\subset Y$
. In this case, we have
From this and Lemma 4.1, we have
![]() $l^{p_1}\subset l^{q_2}$
and
$l^{p_1}\subset l^{q_2}$
and
![]() $l^{q_1}_{v_s}\subset l^{p_2}$
. We only need to verify
$l^{q_1}_{v_s}\subset l^{p_2}$
. We only need to verify
![]() $\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
under the above assumptions (4.4). In fact, we have
$\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
under the above assumptions (4.4). In fact, we have
where we use the embedding relation
![]() $l^{p_1}\subset l^{q_2}$
and
$l^{p_1}\subset l^{q_2}$
and
![]() $l^{q_1}_{v_s}\subset l^{p_2}$
in the first and third inequality respectively, and Lemma 4.2 in the second inequality.
$l^{q_1}_{v_s}\subset l^{p_2}$
in the first and third inequality respectively, and Lemma 4.2 in the second inequality.
Step 3. The goal of this part is to verify that
![]() $Y_1=Z_1$
, where
$Y_1=Z_1$
, where ![]() . Actually, by the definition of
. Actually, by the definition of
![]() $X_1$
,
$X_1$
,
![]() $Z_1=\{(p_1,p_2,q_1,q_2,s)\in X_1: s> A\vee B\vee (A+B)\vee 0=d(1/p_2-1/q_1)\}$
.
$Z_1=\{(p_1,p_2,q_1,q_2,s)\in X_1: s> A\vee B\vee (A+B)\vee 0=d(1/p_2-1/q_1)\}$
.
For
![]() $Y_1\subset Z_1$
, we only need to prove
$Y_1\subset Z_1$
, we only need to prove
![]() $s>d(1/p_2-1/q_1)$
. Using (4.2), we conclude that
$s>d(1/p_2-1/q_1)$
. Using (4.2), we conclude that
Form this and Lemma 4.1, we have
On the other hand, if
![]() $(p_1,p_2,q_1,q_2,s) \in Z_1$
, by Lemma 4.1, we have
$(p_1,p_2,q_1,q_2,s) \in Z_1$
, by Lemma 4.1, we have
From this, we conclude that
where we use the embedding relation
![]() $l^{p_1}\subset l^{q_2}$
and
$l^{p_1}\subset l^{q_2}$
and
![]() $l^{q_1}_{v_s}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
$l^{q_1}_{v_s}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
Step 4. The goal of this part is to verify that
![]() $Y_2=Z_2$
, where
$Y_2=Z_2$
, where ![]() . Actually,
. Actually,
![]() $Z_2=\{(p_1,p_2,q_1,q_2,s)\in X_2: s> A\vee B\vee (A+B)\vee 0=d(1/q_2-1/p_1)\}$
.
$Z_2=\{(p_1,p_2,q_1,q_2,s)\in X_2: s> A\vee B\vee (A+B)\vee 0=d(1/q_2-1/p_1)\}$
.
For
![]() $Y_2\subset Z_2$
, we only need to prove
$Y_2\subset Z_2$
, we only need to prove
![]() $s>=d(1/q_2-1/p_1)$
. Using (4.2), we conclude that
$s>=d(1/q_2-1/p_1)$
. Using (4.2), we conclude that
Form this and Lemma 4.1, we have
On the other hand, if
![]() $(p_1,p_2,q_1,q_2,s) \in Z_2$
, by Lemma 4.1, we have
$(p_1,p_2,q_1,q_2,s) \in Z_2$
, by Lemma 4.1, we have
From this, we conclude that
where we use the embedding relation
![]() $l^{p_1}_{v_s}\subset l^{q_2}$
and
$l^{p_1}_{v_s}\subset l^{q_2}$
and
![]() $l^{q_1}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
$l^{q_1}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
Step 5. The goal of this part is to verify that
![]() $Y_3=Z_3$
, where
$Y_3=Z_3$
, where
![]() $Z_3=Z_{3,1} \cup Z_{3,2}$
with
$Z_3=Z_{3,1} \cup Z_{3,2}$
with

By the definition of
![]() $X_3$
, we have
$X_3$
, we have
![]() $Z_3=X_3 \setminus \{p_1=p_2, s=A+B\}$
.
$Z_3=X_3 \setminus \{p_1=p_2, s=A+B\}$
.
For
![]() $Y_3\subset Z_3$
, we only need to prove that in
$Y_3\subset Z_3$
, we only need to prove that in
![]() $X_3$
the case
$X_3$
the case
![]() $\{p_1=p_2, s=A+B\}$
is not true when
$\{p_1=p_2, s=A+B\}$
is not true when
![]() $\mathcal {T}$
is bounded. We prove this by contradiction, assuming that
$\mathcal {T}$
is bounded. We prove this by contradiction, assuming that
![]() $p_1=p_2=p, s=A+B$
. For a large constant N, take
$p_1=p_2=p, s=A+B$
. For a large constant N, take

Using the inequality (4.3) and the following estimates

and

we obtain the embedding relation
![]() $l^{q_1}_{v_s}\subset l^{q_2}$
by letting
$l^{q_1}_{v_s}\subset l^{q_2}$
by letting
![]() $N\rightarrow \infty $
. Using this embedding relation and Lemma 4.1 with the fact
$N\rightarrow \infty $
. Using this embedding relation and Lemma 4.1 with the fact
![]() $1/q_2>1/q_1$
, we find
$1/q_2>1/q_1$
, we find
![]() $s>d(1/q_2-1/q_1)=A+B$
. This is a contradiction.
$s>d(1/q_2-1/q_1)=A+B$
. This is a contradiction.
We turn to prove that
![]() $Z_3\subset Y_3$
. This proof is divided into two parts:
$Z_3\subset Y_3$
. This proof is divided into two parts:
![]() $Z_{3,1}\subset Y_3$
and
$Z_{3,1}\subset Y_3$
and
![]() $Z_{3,2}\subset Y_3$
.
$Z_{3,2}\subset Y_3$
.
First, let us prove that
![]() $Z_{3,1}\subset Y_3$
. In this case, one can write
$Z_{3,1}\subset Y_3$
. In this case, one can write
![]() $s=s_1+s_2$
with
$s=s_1+s_2$
with
![]() $s_1>A=d(1/p_2-1/q_1)$
and
$s_1>A=d(1/p_2-1/q_1)$
and
![]() $s_2>B=d(1/q_2-1/p_1)$
. From this and
$s_2>B=d(1/q_2-1/p_1)$
. From this and
![]() $A,B>0$
, by Lemma 4.1, we obtain the embedding relations
$A,B>0$
, by Lemma 4.1, we obtain the embedding relations
![]() $l^{p_1}_{v_{s_2}}\subset l^{q_2}$
and
$l^{p_1}_{v_{s_2}}\subset l^{q_2}$
and
![]() $l^{q_1}_{v_{s_1}}\subset l^{p_2}$
. Then the desired conclusion follows by
$l^{q_1}_{v_{s_1}}\subset l^{p_2}$
. Then the desired conclusion follows by
where we use the embedding relation
![]() $l^{p_1}_{v_{s_2}}\subset l^{q_2}$
and
$l^{p_1}_{v_{s_2}}\subset l^{q_2}$
and
![]() $l^{q_1}_{v_{s_1}}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
$l^{q_1}_{v_{s_1}}\subset l^{p_2}$
in the first and third inequalities, respectively, and Lemma 4.2 in the second inequality.
Finally, we turn to the proof of
![]() $Z_{3,2}\subset Y_3$
. In this case, we have
$Z_{3,2}\subset Y_3$
. In this case, we have
![]() $q_2<p_1<p_2<q_1$
and
$q_2<p_1<p_2<q_1$
and
![]() $s=d(1/p_2-1/q_1+1/q_2-1/p_1)$
. We first consider the endpoint case
$s=d(1/p_2-1/q_1+1/q_2-1/p_1)$
. We first consider the endpoint case
![]() $q_1=\infty $
and
$q_1=\infty $
and
![]() $s=d(1/p_2+1/q_2-1/p_1)$
, then the final conclusion follows by using the interpolation argument. In this endpoint case, we write (4.3) as
$s=d(1/p_2+1/q_2-1/p_1)$
, then the final conclusion follows by using the interpolation argument. In this endpoint case, we write (4.3) as

Denote by ![]() . We have
. We have
Then the inequality (4.5) is true if the following one is valid:

This is equivalent to

where
![]() $r_2=p_2/q_2$
,
$r_2=p_2/q_2$
,
![]() $r_1=p_1/q_2$
,
$r_1=p_1/q_2$
, ![]() , and
, and ![]() denotes the fractional integral operator of discrete form. Note that
denotes the fractional integral operator of discrete form. Note that
![]() $r_1, r_2\in (1,\infty )$
,
$r_1, r_2\in (1,\infty )$
, ![]() . The inequality (4.6) follows by the boundedness
. The inequality (4.6) follows by the boundedness ![]() . We refer to [Reference Guo, Fan, Wu and Zhao12] for more details about the boundedness of fractional integral operators.
. We refer to [Reference Guo, Fan, Wu and Zhao12] for more details about the boundedness of fractional integral operators.
Let
![]() $r=q_1/2$
,
$r=q_1/2$
,
![]() $\theta =1/2$
,
$\theta =1/2$
,
![]() $\widetilde {s}=d(1/\widetilde {p_2}-1/\widetilde {q_1}+1/\widetilde {q_2}-1/\widetilde {p_1})$
with
$\widetilde {s}=d(1/\widetilde {p_2}-1/\widetilde {q_1}+1/\widetilde {q_2}-1/\widetilde {p_1})$
with
 $$ \begin{align*} \widetilde{q_1}=\infty,\ \frac{1}{\widetilde{p_1}}=2\bigg(\frac{1}{p_1}-\frac{1}{q_1}\bigg),\ \frac{1}{\widetilde{p_2}}=2\bigg(\frac{1}{p_2}-\frac{1}{q_1}\bigg),\ \frac{1}{\widetilde{q_2}}=2\bigg(\frac{1}{q_2}-\frac{1}{q_1}\bigg). \end{align*} $$
$$ \begin{align*} \widetilde{q_1}=\infty,\ \frac{1}{\widetilde{p_1}}=2\bigg(\frac{1}{p_1}-\frac{1}{q_1}\bigg),\ \frac{1}{\widetilde{p_2}}=2\bigg(\frac{1}{p_2}-\frac{1}{q_1}\bigg),\ \frac{1}{\widetilde{q_2}}=2\bigg(\frac{1}{q_2}-\frac{1}{q_1}\bigg). \end{align*} $$
So we have
![]() $\widetilde {q_2}<\widetilde {p_1}<\widetilde {p_2}<\widetilde {q_1}=\infty $
, and then
$\widetilde {q_2}<\widetilde {p_1}<\widetilde {p_2}<\widetilde {q_1}=\infty $
, and then
![]() $\mathcal {T}\in \mathcal {L}(l^{(\widetilde {p_1},\infty )}_{v_{\widetilde {s}}}({{\mathbb {Z}}^{2d}}), l^{(\widetilde {p_2},\widetilde {q_2})}({{\mathbb {Z}}^{2d}}))$
. Moreover, we have the relations
$\mathcal {T}\in \mathcal {L}(l^{(\widetilde {p_1},\infty )}_{v_{\widetilde {s}}}({{\mathbb {Z}}^{2d}}), l^{(\widetilde {p_2},\widetilde {q_2})}({{\mathbb {Z}}^{2d}}))$
. Moreover, we have the relations
 $$ \begin{align*} \frac{1-\theta}{\widetilde{p_1}}+\frac{\theta}{r}=\frac{1}{p_1},\ \frac{1-\theta}{\widetilde{p_2}}+\frac{\theta}{r}=\frac{1}{p_2},\ \frac{1-\theta}{\widetilde{q_1}}+\frac{\theta}{r}=\frac{1}{q_1},\ \frac{1-\theta}{\widetilde{q_2}}+\frac{\theta}{r}=\frac{1}{q_2}. \end{align*} $$
$$ \begin{align*} \frac{1-\theta}{\widetilde{p_1}}+\frac{\theta}{r}=\frac{1}{p_1},\ \frac{1-\theta}{\widetilde{p_2}}+\frac{\theta}{r}=\frac{1}{p_2},\ \frac{1-\theta}{\widetilde{q_1}}+\frac{\theta}{r}=\frac{1}{q_1},\ \frac{1-\theta}{\widetilde{q_2}}+\frac{\theta}{r}=\frac{1}{q_2}. \end{align*} $$
Then the final conclusion
![]() $\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_{v_s}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
follows by the complex interpolation between the endpoint case
$\mathcal {T}\in \mathcal {L}(l^{(p_1,q_1)}_{v_s}({{\mathbb {Z}}^{2d}}), l^{(p_2,q_2)}({{\mathbb {Z}}^{2d}}))$
follows by the complex interpolation between the endpoint case
![]() $\mathcal {T}\in \mathcal {L}(l^{(\widetilde {p_1},\infty )}_{v_{\widetilde {s}}}({{\mathbb {Z}}^{2d}}), l^{(\widetilde {p_2},\widetilde {q_2})}({{\mathbb {Z}}^{2d}}))$
proved above and the obvious fact
$\mathcal {T}\in \mathcal {L}(l^{(\widetilde {p_1},\infty )}_{v_{\widetilde {s}}}({{\mathbb {Z}}^{2d}}), l^{(\widetilde {p_2},\widetilde {q_2})}({{\mathbb {Z}}^{2d}}))$
proved above and the obvious fact
![]() $\mathcal {T}\in \mathcal {L}(l^{(r,r)},l^{(r,r)})$
.
$\mathcal {T}\in \mathcal {L}(l^{(r,r)},l^{(r,r)})$
.
Accordingly, from above steps, we obtain that
 $$\begin{align*}Y=\bigcup_{j=0}^3 Y_j=\bigcup_{j=0}^3 Z_j. \end{align*}$$
$$\begin{align*}Y=\bigcup_{j=0}^3 Y_j=\bigcup_{j=0}^3 Z_j. \end{align*}$$
Observe that  is precisely the set consists of elements satisfying that:
is precisely the set consists of elements satisfying that: ![]() and s satisfies the conditions in Theorem 1.2. So we complete the proof.
and s satisfies the conditions in Theorem 1.2. So we complete the proof.




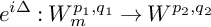
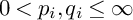 and
and 
