Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Noda, Akio
1987.
Generalized Radon Transform and Lévy’s Brownian Motion, II.
Nagoya Mathematical Journal,
Vol. 105,
Issue. ,
p.
89.
Takenaka, Shigeo
1991.
Integral-geometric construction of self-similar stable processes.
Nagoya Mathematical Journal,
Vol. 123,
Issue. ,
p.
1.
Takenaka, Shigeo
1993.
Stochastic Processes.
p.
303.
Singer, Peter
1994.
An integrated fractional Fourier transform.
Journal of Computational and Applied Mathematics,
Vol. 54,
Issue. 2,
p.
221.
Huang, Zhi-yuan
and
Li, Chu-jin
2005.
Anisotropic Fractional Brownian Random Fields as White Noise Functionals.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 21,
Issue. 4,
p.
655.
Venet, Nil
2019.
Nonexistence of fractional Brownian fields indexed by cylinders.
Electronic Journal of Probability,
Vol. 24,
Issue. none,


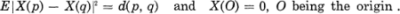 with parameter in a metric space (
with parameter in a metric space (