Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-08T23:48:41.841Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on Differentiable Structures on Real Projective (2n-1)-Spaces

Published online by Cambridge University Press:  22 January 2016

Kenichi Shiraiwa
Kenichi Shiraiwa*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main objective of this paper is to study the action of the group of differentiate structures Γ2n-1 on the (2n-1)-sphere S2n-1 on the diffeomorphism classes on the real projective (2n-1)-space P2n-1 by connected sum. This is done by considering universal covering spaces of the connected sum 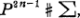where Σ is an exotic (2n-1)-sphere.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 27 , Issue 1 , February 1966 , pp. 357 - 360
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Kervaire-J. Milnor, M., Groups of homotopy spheres, I, Ann. of Math., 77 (1963), 504–537.CrossRefGoogle Scholar
[2] Milnor, J., Sommes de variétés differentiables et structures différentiables des sphères, Bull. Soc. Math. France 87 (1959), 439–444.Google Scholar
[3] Milnor, M. Hirsch-J., Some curious involutions of spheres, Bull. A.M.S. 70 (1964), 372–377.Google Scholar