No CrossRef data available.
Article contents
Rational double points on a normal octic K3 surface
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let S be a normal surface of degree n in 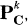 , where (n, k) = (4,3), (6,4) or (8,5). People try to describe all possible combinations of singularities on such surfaces. The case (4,3) is already very complicated. Using properties of K3 surface and elementary transformations of Dynkin Graphs effectively, Urabe [17] was able to solve the problem partially when all singularities are rational double points.
, where (n, k) = (4,3), (6,4) or (8,5). People try to describe all possible combinations of singularities on such surfaces. The case (4,3) is already very complicated. Using properties of K3 surface and elementary transformations of Dynkin Graphs effectively, Urabe [17] was able to solve the problem partially when all singularities are rational double points.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1993
References
[1]
Artin, M., On isolated rational singularities of surface, Amer Math J., 88 (1966).CrossRefGoogle Scholar
[2]
Barth, W., Peters, C., and Vande Ven, A., Compact complex surfaces, Berlin-Heidelberg-New York, Springer, 1984.Google Scholar
[3]
Beauville, R., Complex algebraic surfaces, Cambridge University Press, Cambridge, 1983.Google Scholar
[5]
Conway, J.H. and Sloane, N.J.A., Sphere packings and groups, Berlin-Heidelberg-New York, Springer, 1988.Google Scholar
[6]
Durfee, A.H., Fifteen characterization of rational double points and simple critical points, Lengein, Math., II 25 (1979), 131–163.Google Scholar
[7]
Dynkin, E.B., Semisimple subalgebras of semisimple Lie groups, Amer. Math. Soc. Transl., 6 (1957), 111–244.Google Scholar
[8]
Humphreys, J.E., Introduction to Lie algebra and representatives theory, New York-Heidelberg-Berlin, Springer, 1972.CrossRefGoogle Scholar
[9]
Kawamata, Y., A generalization of Kodaira-Ramanujams vanishing theorem, Math. Ann., 261 (1982), 43–46.Google Scholar
[10]
Milnor, J. and Husemoller, D., Symmetric bilinear forms, Berlin-Heidelberg-New York, Springer, 1972.Google Scholar
[11]
Mumford, D., Algebraic Geometry. Complex projective varieties, Berlin-Heidelberg-New York, Springer, 1976.Google Scholar
[12]
Nikulin, V.V., Integral symmetric bilinear forms and some of their applications, Math. USSR, IV 14 (No.1) (1987), 103–167.Google Scholar
[13]
Saint-Donat, B., Projective models of K 3 surfaces, Amer. J. Math., 96 (1976) 602–639.Google Scholar
[17]
Urabe, T., Elementary transformations of Dynkin Graph and singularities on quartic surfaces, Invent. Math., 87 (1987), 549–572.Google Scholar


