Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mingliang, Fang
and
Hui, Guo
1998.
On unique range sets for meromorphic or entire functions.
Acta Mathematica Sinica, English Series,
Vol. 14,
Issue. 4,
p.
569.
Yi, Hong-Xun
1999.
Some further results on uniqueness of meromorphic functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 38,
Issue. 4,
p.
375.
Shirosaki, Manabu
2000.
Proceedings of the Second ISAAC Congress.
Vol. 7,
Issue. ,
p.
495.
Yang, Lian-Zhong
2000.
Proceedings of the Second ISAAC Congress.
Vol. 7,
Issue. ,
p.
551.
Shiffman, Bernard
2001.
Uniqueness of entire and meromorphic functions sharing finite sets.
Complex Variables, Theory and Application: An International Journal,
Vol. 43,
Issue. 3-4,
p.
433.
Fang, Cai-Yun
and
Fang, Ming-Liang
2002.
Uniqueness of meromorphic functions and differential polynomials.
Computers & Mathematics with Applications,
Vol. 44,
Issue. 5-6,
p.
607.
Xu, Yan
2003.
Meromorphic functions sharing one finite set.
Computers & Mathematics with Applications,
Vol. 45,
Issue. 10-11,
p.
1489.
Fang, Mingliang
and
Zalcman, Lawrence
2003.
Normal families and uniqueness theorems for entire functions.
Journal of Mathematical Analysis and Applications,
Vol. 280,
Issue. 2,
p.
273.
Aihara, Yoshihiro
2004.
Value Distribution Theory and Related Topics.
Vol. 3,
Issue. ,
p.
233.
Okamoto, Takashi
and
Shirosaki, Manabu
2005.
A characterization of collections of two-point sets with the uniqueness property.
Tohoku Mathematical Journal,
Vol. 57,
Issue. 4,
Tan, Tran Van
2005.
Uniqueness polynomials for entire curves into complex projective space.
Analysis,
Vol. 25,
Issue. 4,
Zhang, Jie
and
Xu, Yan
2008.
Meromorphic functions sharing two sets.
Applied Mathematics Letters,
Vol. 21,
Issue. 5,
p.
471.
Gang, Wang
and
Dianxuan, Gong
2012.
Computer, Informatics, Cybernetics and Applications.
Vol. 107,
Issue. ,
p.
649.
Qi, Xiaoguang
Dou, Jia
and
Yang, Lianzhong
2012.
Uniqueness and value distribution for difference operators of meromorphic function.
Advances in Difference Equations,
Vol. 2012,
Issue. 1,
Qi, Xiao-Guang
and
Yang, Lian-Zhong
2013.
SETS AND VALUE SHARING OF q-DIFFERENCES OF MEROMORPHIC FUNCTIONS.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 3,
p.
731.
Banerjee, Abhijit
and
Majumder, Sujoy
2013.
Unique Range Set for Meromorphic Functions with Deficient Values.
Journal of Complex Analysis,
Vol. 2013,
Issue. ,
p.
1.
Banerjee, A.
and
Majumder, S.
2013.
Meromorphic functions with deficiencies generating unique range sets.
Journal of Contemporary Mathematical Analysis,
Vol. 48,
Issue. 6,
p.
310.
刘, 丹
2013.
The Uniqueness of Polynomial Sharing a Set.
Pure Mathematics,
Vol. 03,
Issue. 05,
p.
295.
Qi, Xiaoguang
and
Yang, Lianzhong
2014.
Sharing sets of q-difference of meromorphic functions.
Mathematica Slovaca,
Vol. 64,
Issue. 1,
p.
51.
Lahiri, Indrajit
and
Banerjee, Abhijit
2014.
Analytic Number Theory, Approximation Theory, and Special Functions.
p.
865.


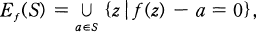
 .
.