Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-02T22:50:56.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective varieties and rings of Thetanullwerte

Published online by Cambridge University Press:  22 January 2016

Riccardo Salvati Manni
Riccardo Salvati Manni*
Affiliation:
Dipartimento di Matematica, Università «La Sapienza», 00185 Roma, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let r denote an even positive integer, m an element of Q2g such that r·m ≡ 0 mod 1 and ϑm the holomorphic function on the Siegel upper-half space Hg defined by

(1) ,

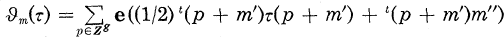in which e(t) stands for exp 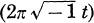and m′ and m″ are the first and the second entry vector of m. Let Θg(r) denote the graded ring generated over C by such Thetanullwerte; then it is a well known fact that the integral closure of Θg(r) is the ring of all modular forms relative to Igusa’s congruence subgroup Γg(r2, 2r2) cf. [6]. We shall denote this ring by A(Γg(r2, 2r2)).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 118 , June 1990 , pp. 165 - 176
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1990

References

[1] Böcherer, S., Über die Fourier-Jaeobi-Entwicklung Siegelscher Eisensteinreihen, Math. Z., 183 (1983), 21–46.CrossRefGoogle Scholar
[2] Böcherer, S., Siegel modular forms and theta series, Proc. Symp. P. Math., 49 (1989).CrossRefGoogle Scholar
[3] Sloane, Conway, Packings, Sphere, Lattices and Groups, Grund Math. Wiss. 290, Springer Verlag, Berlin-Heidelberg-New York (1988).Google Scholar
[4] Elstrodt, J., Eine Charakterisierung der Eisenstein-Reihe zur Siegelschen Modulgruppe,Google Scholar
[5] Freitag, E., Siegelsche Modulfunktionen, Grund. Math. Wiss. 254, Springer Verlag, Berlin-Heidelberg-New York (1983).Google Scholar
[6] Igusa, J., On the graded ring of theta-constants, Amer. J. Math.: I, 86 (1964), 219–246; II, 88 (1966), 221–236.CrossRefGoogle Scholar
[7] Igusa, J., On Siegel modular forms of genus two II, Amer. J. Math., 86 (1964), 392–412.CrossRefGoogle Scholar
[8] Igusa, J., On the variety associated with the ring of thetanullwerte, Amer. J. Math., 103 (1981), 377–398.CrossRefGoogle Scholar
[9] Igusa, J., A desingularization problem in the theory of Siegel modular functions, Math. Ann., 168 (1967), 228–260.CrossRefGoogle Scholar
[10] Igusa, J., On the Nullwerte of jacobians of odd theta functions, Symp. Math., XXIV Google Scholar
[11] Manni, R. Salvati, On the not integrally closed subrings of the ring of the Thetanullwerte II, J. Reine angew. Math., 372 (1986), 64–70.Google Scholar
[12] Manni, R. Salvati, Thetanullwerte and stable modular forms, Amer. J. Math., 111 (1989), 435–455.CrossRefGoogle Scholar
[13] Tsuyumine, S., On Siegel modular forms of degree three, Amer. J. Math., 108 (1986), 755–862.CrossRefGoogle Scholar