Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sinyukova, E. N.
1981.
Geodesic mappings of certain special Riemannian spaces.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 30,
Issue. 6,
p.
946.
Aminova, A. V.
1991.
Groups of transformations of Riemannian manifolds.
Journal of Soviet Mathematics,
Vol. 55,
Issue. 5,
p.
1996.
Sepasi, Maryam
and
Bidabad, Behroz
2014.
On a projectively invariant distance on Finsler spaces of constant negative Ricci scalar.
Comptes Rendus. Mathématique,
Vol. 352,
Issue. 12,
p.
999.
Kiosak, V.
Savchenko, A.
and
Kamienieva, A.
2020.
Geodesic mappings of compact quasi-Einstein spaces with constant scalar curvature.
Vol. 2302,
Issue. ,
p.
040002.


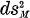 and Ricci tensor Ric
and Ricci tensor Ric