Published online by Cambridge University Press: 22 January 2016
The aim of this paper is to establish the principle of limiting absorption for uniformly propagative systems Λ(x, Dx) = E(x)-1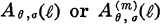 AjDj, Dj = — i∂/∂xj, with perturbations of long-range class, where the perturbation of long-range class, roughly speaking, means that E(x) approaches to E0, E0 being the N × N identity matrix, as | x | → ∞ with order O(| x |-δ), 0 < δ ≦ 1. (The more precise assumptions will be stated below and we require some additional assumptions on the derivatives of E(x).) The spectral and scattering problem for uniformly propagative systems was first formulated by Wilcox [10]. Since then, the principle of limiting absorption has been proved by many authors ([5], [7], [8], [11] etc.). The perturbations discussed in their works belong to the short-range class with δ > 1.
AjDj, Dj = — i∂/∂xj, with perturbations of long-range class, where the perturbation of long-range class, roughly speaking, means that E(x) approaches to E0, E0 being the N × N identity matrix, as | x | → ∞ with order O(| x |-δ), 0 < δ ≦ 1. (The more precise assumptions will be stated below and we require some additional assumptions on the derivatives of E(x).) The spectral and scattering problem for uniformly propagative systems was first formulated by Wilcox [10]. Since then, the principle of limiting absorption has been proved by many authors ([5], [7], [8], [11] etc.). The perturbations discussed in their works belong to the short-range class with δ > 1.