Article contents
On vector bundles on algebraic surfaces and 0-cycles
Published online by Cambridge University Press: 22 January 2016
Extract
Let X be an algebraic complex projective surface equipped with the euclidean topology and E a rank 2 topological vector bundle on X. It is a classical theorem of Wu ([Wu]) that E is uniquely determined by its topological Chern classes 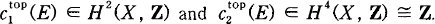 . Viceversa, again a classical theorem of Wu ([Wu]) states that every pair (a, b) ∈ (H (X, Z), Z) arises as topological Chern classes of a rank 2 topological vector bundle. For these results the existence of an algebraic structure on X was not important; for instance it would have been sufficient to have on X a holomorphic structure. In [Sch] it was proved that for algebraic X any such topological vector bundle on X has a holomorphic structure (or, equivalently by GAGA an algebraic structure) if its determinant line bundle has a holomorphic structure. It came as a surprise when Elencwajg and Forster ([EF]) showed that sometimes this was not true if we do not assume that X has an algebraic structure but only a holomorphic one (even for some two dimensional tori (see also [BL], [BF], or [T])).
. Viceversa, again a classical theorem of Wu ([Wu]) states that every pair (a, b) ∈ (H (X, Z), Z) arises as topological Chern classes of a rank 2 topological vector bundle. For these results the existence of an algebraic structure on X was not important; for instance it would have been sufficient to have on X a holomorphic structure. In [Sch] it was proved that for algebraic X any such topological vector bundle on X has a holomorphic structure (or, equivalently by GAGA an algebraic structure) if its determinant line bundle has a holomorphic structure. It came as a surprise when Elencwajg and Forster ([EF]) showed that sometimes this was not true if we do not assume that X has an algebraic structure but only a holomorphic one (even for some two dimensional tori (see also [BL], [BF], or [T])).
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1993
References
- 1
- Cited by


