No CrossRef data available.
Article contents
On the rank of the first radical layer of a p-class group of an algebraic number field
Published online by Cambridge University Press: 22 January 2016
Abstract
Let p be a prime number. Let M be a finite Galois extension of a finite algebraic number field k. Suppose that M contains a primitive pth root of unity and that the p-Sylow subgroup of the Galois group G = Gal(M/k) is normal. Let K be the intermediate field corresponding to the p-Sylow subgroup. Let 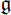 = Gal(K/k). The p-class group C of M is a module over the group ring ZpG, where Zp is the ring of p-adic integers. Let J be the Jacobson radical of ZpG. C/JC is a module over a semisimple artinian ring Fp
= Gal(K/k). The p-class group C of M is a module over the group ring ZpG, where Zp is the ring of p-adic integers. Let J be the Jacobson radical of ZpG. C/JC is a module over a semisimple artinian ring Fp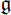 . We study multiplicity of an irreducible representation Φ apperaring in C/JC and prove a formula giving this multiplicity partially. As application to this formula, we study a cyclotomic field M such that the minus part of C is cyclic as a ZpG-module and a CM-field M such that the plus part of C vanishes for odd p.
. We study multiplicity of an irreducible representation Φ apperaring in C/JC and prove a formula giving this multiplicity partially. As application to this formula, we study a cyclotomic field M such that the minus part of C is cyclic as a ZpG-module and a CM-field M such that the plus part of C vanishes for odd p.
To show the formula, we apply theory of central extensions of algebraic number field and study global and local Kummer duality between the genus group and the Kummer radical for the genus field with respect to M/K.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1999


