Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kanzaki, Teruo
1978.
On the category of commutative algebras split by a faithfully flat extension.
Journal of Algebra,
Vol. 55,
Issue. 2,
p.
455.
Micali, A.
and
Paques, A.
1982.
Le group des algebras quadratiques(∗)..
Communications in Algebra,
Vol. 10,
Issue. 16,
p.
1765.
El-agawany, M.
1987.
Algebre mesonique d'une forme multilineaire symetrique.
Communications in Algebra,
Vol. 15,
Issue. 12,
p.
2431.
Kanzaki, Teruo
1989.
Totally real commutative algebras.
Communications in Algebra,
Vol. 17,
Issue. 9,
p.
2179.
Helmstetter, Jacques
Micali, Artibano
and
Revoy, Philippe
2012.
Generalized quadratic modules.
Afrika Matematika,
Vol. 23,
Issue. 1,
p.
53.
Helmstetter, Jacques
Micali, Artibano
and
Revoy, Philippe
2014.
On the Definition of Quadratic Mappings.
Advances in Applied Clifford Algebras,
Vol. 24,
Issue. 1,
p.
125.
Voight, John
2016.
Discriminants and the monoid of quadratic rings.
Pacific Journal of Mathematics,
Vol. 283,
Issue. 2,
p.
483.
Helmstetter, Jacques
2020.
Kanzaki’s Generalized Quadratic Spaces and Graded Salingaros Groups.
Advances in Applied Clifford Algebras,
Vol. 30,
Issue. 4,
Orelma, Heikki
2023.
Analysis on generalized Clifford algebras.
Вестник Самарского государственного технического университета. Серия «Физико-математические науки»,
Vol. 27,
Issue. 1,
p.
7.
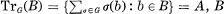 is a quadratic extension of A. A generalized crossed product Δ(f, A, Φ, G) of a ring A and a group G of order 2, in [4], is also a quadratic extension of A.
is a quadratic extension of A. A generalized crossed product Δ(f, A, Φ, G) of a ring A and a group G of order 2, in [4], is also a quadratic extension of A.