No CrossRef data available.
Article contents
On the Lp bound for degenerate elliptic operators with two variables in the ill posed problem1)
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Ω be an open set in the upper half plane {y > 0}, whose boundary is denoted by ∂Ω. Let ∂Ω contain an open segment Γ lying on the x-axis.
We consider the following system of first order degenerating on y = 0:
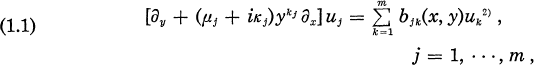
where kj, μj are real constants and bjk are in L∞(Ω), further kj are non-negative integers.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1982
Footnotes
1)
This work has been supported by Grant-in-Aid for Co-operative Research A organized by the Ministry of Education, the Japanese Government.
References
[1]
Carleman, T., Sur un probleme d’unicité pour les systèmes d’équations aux dérivées partielles à deux variables indépendentes, Arkiv Mat., 26B (1938), 1–9.Google Scholar
[2]
John, F., Continuous dependence on data for solutions of partial differential equations with a prescribed bound, Comm. Pure Appl. Math., 13 (1960), 551–585.CrossRefGoogle Scholar
[3]
Payne, L. E. and Sather, D., On some improperly posed problems for the Chaplygin equation, J. Math. Anal. Appl., 19 (1967), 67–77.CrossRefGoogle Scholar
[4]
Saut, J. C. and Scheurer, B., Un théorème de prolongement unique pour des opérateurs elliptiques dont les coefficients ne sont pas localement bornés, C. R. Acad. Sci. Paris, 290 (1980), 595–598.Google Scholar


