Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T21:24:06.900Z Has data issue: false hasContentIssue false
  • English
  • Français

On the invariant differential metrics near pseudoconvex boundary points where the Levi form has corank one

Published online by Cambridge University Press:  22 January 2016

Gregor Herbort
Gregor Herbort*
Affiliation:
Bergische Universitaet-Gesamthochschule Wuppertal, Fachbereich Mathematik, Gaussstrasse 20 D-56, Wuppertal 1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a bounded domain in Cn; in the space L2(D) of functions on D which are square-integrable with respect to the Lebesgue measure d2nz the holomorphic functions form a closed subspace H2(D). Therefore there exists a well-defined orthogonal projection PD: L2(D) → H2(D) with an integral kernel KD:D × D → C, the Bergman kernel function of D. An explicit computation of this function directly from the definition is possible only in very few cases, as for instance the unit ball, the complex “ellipsoids” 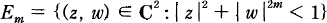, or the annulus in the plane. Also, there is no hope of getting information about the function KD in the interior of a general domain. Therefore the question for an asymptotic formula for the Bergman kernel near the boundary of D arises.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 130 , June 1993 , pp. 25 - 54
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[A] d’Angelo, J. P., Real hypersurfaces, orders of contact, and applications, Ann. of Math., 115 (1982), 615–637.Google Scholar
[Be] Bergman, S., Über die Kernfunktion eines Bereiches und ihr Verhalten am Rande, I., Crelle’s J. Reine Angew. Math., 169 (1933), 1–42.Google Scholar
[B-F] Bedford-J., E. Fornaess, E., Biholomorphic maps of weakly pseudoconvex donains, Duke Math., J., 45,4(1978), 711–719.Google Scholar
[B-S] Boutet, L. Monvel-J, de. Sjöstrand, Sur la singularité des noyaux de Bergman et de Szegö, Soc. Math, de France, Astérisque, 34–35 (1976), 123–164.Google Scholar
[C1] Catlin, D. W., Estimation of invariant metrics on pseudoconvex domains of dimension two, Math. Z., 200,3 (1989), 429–466.CrossRefGoogle Scholar
[C2] Catlin, D. W., Global Regularity of the d-Neumann Problem, Proceedings of Symposia in Pure Mathematics, vol. 41, 1984, pp. 39–49.CrossRefGoogle Scholar
[Di 1] Diederich, K., Das Randverhalten der Bergmanschen Kernfunktion und Metrik in streng pseudokonvexen Gebieten, Math. Ann., 189 (1970), 9–36.Google Scholar
[Di 2] Diederich, K., Uber die 1. und 2. Ableitungen der Bergmanschen Kernfunktion und ihr Randverhalten, Math. Ann., 203 (1973), 129–170.Google Scholar
[D-F 1] Diederich-J., K. E-Fornaess, , Pseudoconvex domains: Existence of Stein neighborhoods, Duke Math. J., 44,3 (1977), 641–662.Google Scholar
[D-F 2] Diederich-J., K. E-Fornaess, , Pseudoconvex domains: Bounded strictly plurisubharmonic exhaustion functions, Invent. Math., 39 (1977), 129–141.CrossRefGoogle Scholar
[D-H-O] Diederich-G., K. Ohsawa, Herbort-T., The Bergman kernel on uniformly extendable pseudoconvex domains, Math. Ann., 273 (1986), 471–478.Google Scholar
[F] Fefferman, Ch. L., The Bergman kernel and biholomorphic mappings of pseudoconvex domains, Invent. Math., 26 (1974), 1–65.Google Scholar
[F-S] Fornœss-N, J. E.. Sibony, Construction of p. 1. s. functions on weakly pseudoconvex domains, Duke Math. J., 58,3 (1989), 633–655.Google Scholar
[Gr] Graham, I., Boundary behavior of the Caratheodory and Kobayashi metrics on strongly pseudoconvex domains in C with smooth boundary, Trans. Amer. Math. Soc, 207 (1975), 219–239.Google Scholar
[H] Henkin, G. M., An analytic polyhedron is not holomorphically equivalent to a strictly pseudoconvex domain, Soviet Math. Dokl., 14 (1973), 858–862.Google Scholar
[He 1] Herbort, G., Uber das Randverhalten der Bergmanschen Kernfunktion einer speziellen Klasse schwach pseudokonexer Gebiete des C n , Math. Z., 184 (1983), 193–202.Google Scholar
[He 2] Herbort, G., Logarithmic growth of the Bergman kernel for weakly pseudoconvex domains in C of finite type, Manuscripta Math., 45 (1983), 69–76.CrossRefGoogle Scholar
[He 3] Invariant metrics and peak functions on pseudoconvex domains of homogeneous finite diagonal type, Math. Z., 209 (1992) 223–243.Google Scholar
[Hör] Hörmander, L., An Introduction to Complex Analysis in Several Variables, Van Nostrand, North Holland Publication Company, 1973.Google Scholar
[K 1] Kohn, J. J., Harmonic Integrals on Strongly Pseudoconvex Manifolds, I., Ann. of Math., 78(1963), 112–148.Google Scholar
[K 2] Kohn, J. J., Boundary behavior of d on weakly pseudoconvex manifolds of dimension two, J. Differential Geom., 6 (1972), 523–542.Google Scholar
[K 3] Kohn, J. J., Global regularity for d on weakly pseudoconvex manifolds, Trans. Amer. Math. Soc., 181 (1973), 273–292.Google Scholar
[N-S-W] Nagel-E., A. Wainger, Stein-S., Balls and metrics defined by vector fields I, Acta Math., 155 (1985), 103–147.Google Scholar
[Oh] Ohsawa, T., Boundary Behavior of the Bergman Kernel Function on Pseudoconvex Domains, Publications of the R. I. M.S., Kyoto University, 20 (1984), 897–902.Google Scholar
[R] Range, M., The Caratheodory metric and holomorphic maps on a class of weakly pseudoconvex domains, Pacific Journal Math., 78,1 (1978), 173–189.Google Scholar