Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-03T09:02:12.113Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Existence of the Resolvent Kernel for Elliptic Differential Operator in a Compact Riemann Space

Published online by Cambridge University Press:  22 January 2016

Kôsaku Yosida
Kôsaku Yosida*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the differential operator

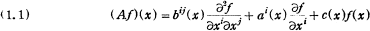
in an n-dimensional (n≧2), orientiable, compact Riemann space R with the metric ds2 = gij(x)dxidxj. Here bij(x) is a contravariant tensor such that the quadratic form 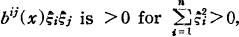and ai(x) changes, by the coordininates transformation x → x̅, as follows:

.

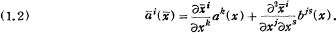Type
Research Article
Information
Nagoya Mathematical Journal , Volume 4 , June 1952 , pp. 63 - 72
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1952

References

1) Yosida, Ko: Integrability of the backward diffusion equation in a compact Riemannian space, Nagoya Math. Journal, Vol. 3, 1-4 (1951)CrossRefGoogle Scholar. At this juncture, the author wishes to correct the errata in the cited paper, (−m-1 Ã) on page 3, line 2 must be corrected as (I−m-1 Ã), D(A) and A on page 3, line 5 must be corrected as D(Im ) and Im respecteively.

2) Schwartz, L.: Théorie des distributions, Paris (1950).Google Scholar

3) Cf.Yosida, K.: Integration of Fokker-Planck’s equation with a boundary condition, Journal of the Math. Soc. of Japan, Vol. 3, No. 1, 69-73 (1951).CrossRefGoogle Scholar

4) We follow Thomas, T. Y. and Titt, E. W.: On the elementary solution of the general linear differential equation of the second order with analytic coefficients, Journal de Math., tome 18, 217-248 (1939).Google Scholar

5) The same result is proved in other ways by Kodaira, K. (unpublished) and by Minakshsundarum, S. and Pleijel, A.: Some properties of the eigenfunctions of the Laplace- operator on Riemannian manifolds, Canadian Journal of Math., Vol. 1, 242-256 (1950).Google Scholar

6) Schwartz: ibid.

7) Schwartz: ibid.

8) Cf.Yosida, K.: Brownian motion on the surface of the 3-sphere, Ann. of Math. Statistics, Vol. 20, 292-296 (1949).Google Scholar