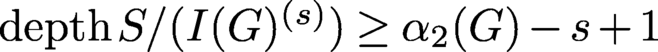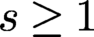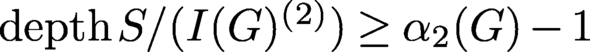Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Seyed Fakhari, S.A.
2024.
Lower bounds for the depth of symbolic powers of edge ideals of graphs.
Journal of Algebra,
Vol. 639,
Issue. ,
p.
422.
Seyed Fakhari, S. A.
2024.
Lower bounds for the depth of the second power of edge ideals.
Collectanea Mathematica,
Vol. 75,
Issue. 2,
p.
535.