Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-08T07:54:39.365Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Clifford Collineation, Transform and Similarity Groups (IV): An Application to Quadratic Forms

Published online by Cambridge University Press:  22 January 2016

G. E. Wall
G. E. Wall*
Affiliation:
University of Sydney, New South Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

E. S. Barnes and I recently constructed a series of positive quadratic forms fN in N = 2n variables (n = 1, 2,…) with relative minima of order 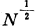for large N. I continue this investigation by determining the minimal vectors of fN and showing that, for 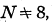its group of automorphs is the Clifford group 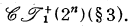This suggests a generalization. Replacing by 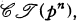where p is an odd prime, I derive a new series of positive forms in N =(p−1)pn variables (§4). The relative minima are again of order 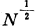(p fixed, N → ∞ ), the “best” forms being those for p = 3, 5. All forms are eutactic though only those for p = 3,5 are extreme.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 21 , December 1962 , pp. 199 - 222
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1962

References

[1] Barnes, E. S. and Wall, G. E., Some extreme forms defined in terms of Abelian groups, J. Australian Math. Soc. 1 (1959), 47–63.CrossRefGoogle Scholar
[2], [3] Bolt, Beverley, Room, T. G. and Wall, G. E., On the Clifford collineation, transform and similarity groups (I) and (II), J. Australian Math. Soc. 2 (1961), 60–96.Google Scholar
[4] Coxeter, H. S. M., Extreme forms, Canad. J. Maths. 3 (1951), 391–441.Google Scholar
[5] Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups (Springer, 1957).Google Scholar
[6] Dieudonné, J., La geometrie des groupes classiques (Springer, 1955).Google Scholar