Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Namikawa, Yukihiko
1974.
Classification of Algebraic Varieties and Compact Complex Manifolds.
Vol. 412,
Issue. ,
p.
165.
Nakamura, Iku
1975.
On moduli of stable quasi abelian varieties.
Nagoya Mathematical Journal,
Vol. 58,
Issue. ,
p.
149.
Namikawa, Yukihiko
1976.
A new compactification of the Siegel space and degeneration of Abelian varieties. I.
Mathematische Annalen,
Vol. 221,
Issue. 2,
p.
97.
Namikawa, Yukihiko
1976.
A new compactification of the Siegel space and degeneration of Abelian varieties. II.
Mathematische Annalen,
Vol. 221,
Issue. 3,
p.
201.
van Geemen, Bert
1984.
Siegel modular forms vanishing on the moduli space of curves.
Inventiones mathematicae,
Vol. 78,
Issue. 2,
p.
329.
Charney, Ruth
and
Lee, Ronnie
1984.
Moduli space of stable curves from a homotopy viewpoint.
Journal of Differential Geometry,
Vol. 20,
Issue. 1,
Oda, Tadao
1985.
Recent Progress of Algebraic Geometry in Japan.
Vol. 73,
Issue. ,
p.
188.
friedman, Robert
and
Smith, Roy
1986.
Degenerations of Prym varieties and intersections of three quadrics.
Inventiones Mathematicae,
Vol. 85,
Issue. 3,
p.
615.
Kato, A.
Matsuo, Y.
and
Odake, S.
1986.
Modular invariance and two-loop bosonic string vacuum amplitude.
Physics Letters B,
Vol. 179,
Issue. 3,
p.
241.
Donagi, Ron
1987.
Big Schottky.
Inventiones Mathematicae,
Vol. 89,
Issue. 3,
p.
569.
Kawamoto, Noboru
Namikawa, Yukihiko
Tsuchiya, Akihiro
and
Yamada, Yasuhiko
1988.
Geometric realization of conformal field theory on Riemann surfaces.
Communications in Mathematical Physics,
Vol. 116,
Issue. 2,
p.
247.
González Díez, Gabino
and
Harvey, William J.
1991.
On complete curves in moduli space II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 3,
p.
467.
Gerritzen, L.
1992.
Equations defining the periods of totally degenerate curves.
Israel Journal of Mathematics,
Vol. 77,
Issue. 1-2,
p.
187.
Brownstein, Alan
and
Lee, Ronnie
1992.
Cohomology of the symplectic group 𝑆𝑝₄(𝑍). I. The odd torsion case.
Transactions of the American Mathematical Society,
Vol. 334,
Issue. 2,
p.
575.
Liu, Qing
1993.
Courbes stables de genre 2 et leur sch�ma de modules.
Mathematische Annalen,
Vol. 295,
Issue. 1,
p.
201.
Asada, Mamoru
Matsumoto, Makoto
and
Oda, Takayuki
1995.
Local monodromy on the fundamental groups of algebraic curves along a degenerate stable curve.
Journal of Pure and Applied Algebra,
Vol. 103,
Issue. 3,
p.
235.
Alexeev, V.
Birkenhake, Ch.
and
Hulek, K.
2002.
Degenerations of Prym varieties.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 553,
Hassett, Brendan
2005.
Geometric Methods in Algebra and Number Theory.
Vol. 235,
Issue. ,
p.
169.
Bainbridge, Matt
2007.
Euler characteristics of Teichmüller curves in genus two.
Geometry & Topology,
Vol. 11,
Issue. 4,
p.
1887.
Brannetti, Silvia
Melo, Margarida
and
Viviani, Filippo
2011.
On the tropical Torelli map.
Advances in Mathematics,
Vol. 226,
Issue. 3,
p.
2546.


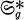 the coarse moduli space of principally polarized abelian varieties of dimension
the coarse moduli space of principally polarized abelian varieties of dimension