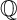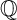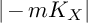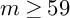1 Introduction
Throughout this paper, we work over an algebraically closed field of characteristic
![]() $0$
(e.g., the complex number field
$0$
(e.g., the complex number field
![]() $\mathbb {C}$
). We adopt standard notation in [Reference Kollár and Mori14].
$\mathbb {C}$
). We adopt standard notation in [Reference Kollár and Mori14].
A normal projective variety X is called a weak
![]() ${\mathbb {Q}}$
-Fano variety (resp.
${\mathbb {Q}}$
-Fano variety (resp.
![]() ${\mathbb {Q}}$
-Fano variety) if
${\mathbb {Q}}$
-Fano variety) if
![]() $-K_X$
is nef and big (resp. ample). According to the minimal model program, (weak)
$-K_X$
is nef and big (resp. ample). According to the minimal model program, (weak)
![]() ${\mathbb {Q}}$
-Fano varieties form a fundamental class in birational geometry. Motivated by the classification theory of three-dimensional algebraic varieties, we are interested in the study of explicit geometry of (weak)
${\mathbb {Q}}$
-Fano varieties form a fundamental class in birational geometry. Motivated by the classification theory of three-dimensional algebraic varieties, we are interested in the study of explicit geometry of (weak)
![]() ${\mathbb {Q}}$
-Fano varieties with terminal or canonical singularities. In this direction, there are a lot of works in the literature (see, e.g., [Reference Chen and Chen2], [Reference Chen4]–[Reference Chen and Jiang6], [Reference Jiang10]–[Reference Jiang and Zou12], [Reference Prokhorov16]–[Reference Prokhorov19]).
${\mathbb {Q}}$
-Fano varieties with terminal or canonical singularities. In this direction, there are a lot of works in the literature (see, e.g., [Reference Chen and Chen2], [Reference Chen4]–[Reference Chen and Jiang6], [Reference Jiang10]–[Reference Jiang and Zou12], [Reference Prokhorov16]–[Reference Prokhorov19]).
Given a terminal weak
![]() $\mathbb {Q}$
-Fano threefold X, the mth anti-canonical map
$\mathbb {Q}$
-Fano threefold X, the mth anti-canonical map
![]() $\varphi _{-m, X}$
(or simply
$\varphi _{-m, X}$
(or simply
![]() $\varphi _{-m}$
) is the rational map induced by the linear system
$\varphi _{-m}$
) is the rational map induced by the linear system
![]() $|-mK_X|$
. We are interested in the fundamental question of finding an optimal integer
$|-mK_X|$
. We are interested in the fundamental question of finding an optimal integer
![]() $c_3$
such that
$c_3$
such that
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq c_3$
. The existence of such
$m\geq c_3$
. The existence of such
![]() $c_3$
follows from the boundedness result in [Reference Kollár, Miyaoka, Mori and Takagi13]. More generally, Birkar [Reference Birkar1] showed that, for a positive integer d, there exists a positive integer
$c_3$
follows from the boundedness result in [Reference Kollár, Miyaoka, Mori and Takagi13]. More generally, Birkar [Reference Birkar1] showed that, for a positive integer d, there exists a positive integer
![]() $c_d$
such that
$c_d$
such that
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq c_d$
and for all terminal weak
$m\geq c_d$
and for all terminal weak
![]() $\mathbb {Q}$
-Fano d-folds, which is one important step toward the solution of the Borisov–Alexeev–Borisov conjecture. The following example shows that
$\mathbb {Q}$
-Fano d-folds, which is one important step toward the solution of the Borisov–Alexeev–Borisov conjecture. The following example shows that
![]() $c_3\geq 33$
.
$c_3\geq 33$
.
Example 1.1 [Reference Iano-Fletcher8, List 16.6, No. 95]
A general weighted hypersurface
![]() $X_{66}\subset \mathbb {P}(1, 5, 6$
,
$X_{66}\subset \mathbb {P}(1, 5, 6$
,
![]() $22, 33)$
is a
$22, 33)$
is a
![]() $\mathbb {Q}$
-factorial terminal
$\mathbb {Q}$
-factorial terminal
![]() $\mathbb {Q}$
-Fano threefold of Picard number
$\mathbb {Q}$
-Fano threefold of Picard number
![]() $1$
with
$1$
with
![]() $\varphi _{-m}$
birational for
$\varphi _{-m}$
birational for
![]() $m\geq 33$
but
$m\geq 33$
but
![]() $\varphi _{-32}$
not birational.
$\varphi _{-32}$
not birational.
In [Reference Chen and Jiang5], it was showed that for a terminal weak
![]() $\mathbb {Q}$
-Fano threefold X,
$\mathbb {Q}$
-Fano threefold X,
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 97$
, which seems far from being optimal comparing to Example 1.1. Later in [Reference Chen and Jiang6], it was showed that any terminal weak
$m\geq 97$
, which seems far from being optimal comparing to Example 1.1. Later in [Reference Chen and Jiang6], it was showed that any terminal weak
![]() $\mathbb {Q}$
-Fano threefold is birational to some terminal weak
$\mathbb {Q}$
-Fano threefold is birational to some terminal weak
![]() $\mathbb {Q}$
-Fano threefold Y such that
$\mathbb {Q}$
-Fano threefold Y such that
![]() $\varphi _{-m, Y}$
is birational for all
$\varphi _{-m, Y}$
is birational for all
![]() $m\geq 52$
. Moreover, in recent works [Reference Jiang10], [Reference Jiang11], we can make use of the behavior of the pluri-anti-canonical maps studied in [Reference Chen and Jiang5] in the classification of terminal
$m\geq 52$
. Moreover, in recent works [Reference Jiang10], [Reference Jiang11], we can make use of the behavior of the pluri-anti-canonical maps studied in [Reference Chen and Jiang5] in the classification of terminal
![]() $\mathbb {Q}$
-Fano threefolds. So we believe that a better understanding of the behavior of the pluri-anti-canonical maps (including new methods developed during the approach) will help us understand the classification of terminal
$\mathbb {Q}$
-Fano threefolds. So we believe that a better understanding of the behavior of the pluri-anti-canonical maps (including new methods developed during the approach) will help us understand the classification of terminal
![]() $\mathbb {Q}$
-Fano threefolds better.
$\mathbb {Q}$
-Fano threefolds better.
The main goal of this paper is to give an improvement of [Reference Chen and Jiang5], [Reference Chen and Jiang6] without passing to a birational model. The main theorem of this paper is the following.
Theorem 1.2. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Then the mth anti-canonical map
${\mathbb {Q}}$
-Fano threefold. Then the mth anti-canonical map
![]() $\varphi _{-m}$
defined by
$\varphi _{-m}$
defined by
![]() $|-mK_X|$
is birational for all
$|-mK_X|$
is birational for all
![]() $m\geq 59$
.
$m\geq 59$
.
Remark 1.3. Theorem 1.2 holds for canonical weak
![]() ${\mathbb {Q}}$
-Fano threefolds by taking a
${\mathbb {Q}}$
-Fano threefolds by taking a
![]() ${\mathbb {Q}}$
-factorial terminalization by [Reference Kollár and Mori14, Ths. 6.23 and 6.25].
${\mathbb {Q}}$
-factorial terminalization by [Reference Kollár and Mori14, Ths. 6.23 and 6.25].
For terminal
![]() ${\mathbb {Q}}$
-Fano threefolds, we have a slightly better bound.
${\mathbb {Q}}$
-Fano threefolds, we have a slightly better bound.
Theorem 1.4. Let X be a terminal
![]() ${\mathbb {Q}}$
-Fano threefold. Then the mth anti-canonical map
${\mathbb {Q}}$
-Fano threefold. Then the mth anti-canonical map
![]() $\varphi _{-m}$
defined by
$\varphi _{-m}$
defined by
![]() $|-mK_X|$
is birational for all
$|-mK_X|$
is birational for all
![]() $m\geq 58$
.
$m\geq 58$
.
To prove the main theorem, we already have several criteria to determine the birationality in [Reference Chen and Jiang5], [Reference Chen and Jiang6], which are optimal in many cases (cf. [Reference Chen and Jiang5, Exam. 5.12]). In order to study the birationality of
![]() $|-mK_X|$
, as indicated in [Reference Chen4]–[Reference Chen and Jiang6], it is crucial to study when
$|-mK_X|$
, as indicated in [Reference Chen4]–[Reference Chen and Jiang6], it is crucial to study when
![]() $|-mK_X|$
is not composed with a pencil. In fact, finding a criterion for
$|-mK_X|$
is not composed with a pencil. In fact, finding a criterion for
![]() $|-mK_X|$
not composed with a pencil is one of the central problems in [Reference Chen and Jiang5], [Reference Chen and Jiang6] (see [Reference Chen and Jiang5, Prob. 1.3], [Reference Chen and Jiang6, Prob. 1.5]). Comparing to the birationality criteria, the non-pencil criteria in [Reference Chen and Jiang5], [Reference Chen and Jiang6] are not satisfactory. As one of the main ingredients of this paper, we give a new criterion for
$|-mK_X|$
not composed with a pencil is one of the central problems in [Reference Chen and Jiang5], [Reference Chen and Jiang6] (see [Reference Chen and Jiang5, Prob. 1.3], [Reference Chen and Jiang6, Prob. 1.5]). Comparing to the birationality criteria, the non-pencil criteria in [Reference Chen and Jiang5], [Reference Chen and Jiang6] are not satisfactory. As one of the main ingredients of this paper, we give a new criterion for
![]() $|-mK_X|$
not composed with a pencil.
$|-mK_X|$
not composed with a pencil.
Theorem 1.5 (=Theorem 4.2)
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
for some positive integer m, then
![]() $|-mK_X|$
is not composed with a pencil.
$|-mK_X|$
is not composed with a pencil.
The following special case is already interesting for the study of anti-canonical systems of terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds, and might have applications on upper bounds of degrees of terminal weak
${\mathbb {Q}}$
-Fano threefolds, and might have applications on upper bounds of degrees of terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds (cf. [Reference Prokhorov16], [Reference Prokhorov17]).
${\mathbb {Q}}$
-Fano threefolds (cf. [Reference Prokhorov16], [Reference Prokhorov17]).
Corollary 1.6. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $h^0(X,-K_X)>13$
, then
$h^0(X,-K_X)>13$
, then
![]() $|-K_X|$
is not composed with a pencil.
$|-K_X|$
is not composed with a pencil.
The paper is organized as follows: in §2, we recall basic knowledge. In §3, we recall the birationality criteria of terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds in [Reference Chen and Jiang5], [Reference Chen and Jiang6] with some generalizations. In §4, we prove the new criterion Theorem 4.2 and give an effective method to apply it. In §5, we prove the main results.
${\mathbb {Q}}$
-Fano threefolds in [Reference Chen and Jiang5], [Reference Chen and Jiang6] with some generalizations. In §4, we prove the new criterion Theorem 4.2 and give an effective method to apply it. In §5, we prove the main results.
Notation
For the convenience of readers, we list here the notation that will be frequently used in this paper. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold.
${\mathbb {Q}}$
-Fano threefold.

2 Preliminaries
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Denote by
${\mathbb {Q}}$
-Fano threefold. Denote by
![]() $r_X$
the Cartier index of
$r_X$
the Cartier index of
![]() $K_X$
. For any positive integer m, the number
$K_X$
. For any positive integer m, the number
![]() $P_{-m}=h^0(X, {\mathcal {O}}_X(-mK_X))$
is called the mth anti-plurigenus of X and
$P_{-m}=h^0(X, {\mathcal {O}}_X(-mK_X))$
is called the mth anti-plurigenus of X and
![]() $\varphi _{-m}$
denotes the mth anti-canonical map defined by
$\varphi _{-m}$
denotes the mth anti-canonical map defined by
![]() $|-mK_X|$
.
$|-mK_X|$
.
2.1 The fibration induced by
 $|D|$
$|D|$
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Consider a
${\mathbb {Q}}$
-Fano threefold. Consider a
![]() ${\mathbb {Q}}$
-Cartier Weil divisor D on X with
${\mathbb {Q}}$
-Cartier Weil divisor D on X with
![]() $h^0(X, D)\geq 2$
. Then there is a rational map defined by
$h^0(X, D)\geq 2$
. Then there is a rational map defined by
![]() $|D|$
:
$|D|$
:
By Hironaka’s desingularization theorem, we can take a projective birational morphism
![]() $\pi : W \rightarrow X$
such that:
$\pi : W \rightarrow X$
such that:
-
(i) W is smooth.
-
(ii) The movable part
 $|M|$
of
$|M|$
of
 $|\lfloor \pi ^*(D)\rfloor |$
is base-point-free and, consequently,
$|\lfloor \pi ^*(D)\rfloor |$
is base-point-free and, consequently,
 $\gamma :=\Phi _{|D|}\circ \pi $
is a morphism.
$\gamma :=\Phi _{|D|}\circ \pi $
is a morphism. -
(iii) The sum of
 $\pi _{*}^{-1}(D)$
and the exceptional divisors of
$\pi _{*}^{-1}(D)$
and the exceptional divisors of
 $\pi $
has simple normal crossing support.
$\pi $
has simple normal crossing support.
Let
![]() $W \stackrel {f}{\longrightarrow } \Gamma \stackrel {s}{\longrightarrow } Z$
be the Stein factorization of
$W \stackrel {f}{\longrightarrow } \Gamma \stackrel {s}{\longrightarrow } Z$
be the Stein factorization of
![]() $\gamma $
with
$\gamma $
with
![]() $Z:=\gamma (W) \subset \mathbb {P}^{h^0(X, D)-1}$
. We have the following commutative diagram:
$Z:=\gamma (W) \subset \mathbb {P}^{h^0(X, D)-1}$
. We have the following commutative diagram:

If
![]() $\dim (\Gamma )\geq 2$
, then a general member S of
$\dim (\Gamma )\geq 2$
, then a general member S of
![]() $|M|$
is a smooth projective surface by Bertini’s theorem. In this case,
$|M|$
is a smooth projective surface by Bertini’s theorem. In this case,
![]() $|D|$
is said to be not composed with a pencil of surfaces (not composed with a pencil, for short).
$|D|$
is said to be not composed with a pencil of surfaces (not composed with a pencil, for short).
If
![]() $\dim (\Gamma )=1$
, then
$\dim (\Gamma )=1$
, then
![]() $\Gamma \cong \mathbb {P}^{1}$
as
$\Gamma \cong \mathbb {P}^{1}$
as
![]() $h^1(\Gamma , \mathcal {O}_\Gamma )\leq h^1(W, \mathcal {O}_W)=h^1(X, \mathcal {O}_X)=0$
. Furthermore, a general fiber S of f is a smooth projective surface by Bertini’s theorem. In this case,
$h^1(\Gamma , \mathcal {O}_\Gamma )\leq h^1(W, \mathcal {O}_W)=h^1(X, \mathcal {O}_X)=0$
. Furthermore, a general fiber S of f is a smooth projective surface by Bertini’s theorem. In this case,
![]() $|D|$
is said to be composed with a (rational) pencil of surfaces (composed with a pencil, for short).
$|D|$
is said to be composed with a (rational) pencil of surfaces (composed with a pencil, for short).
In each case, S is called a generic irreducible element of
![]() $|M|$
. We can also define a generic irreducible element of a moving linear system on a surface in the similar way.
$|M|$
. We can also define a generic irreducible element of a moving linear system on a surface in the similar way.
Definition 2.1. Keep the same notation as above. Let
![]() $D'$
be another
$D'$
be another
![]() ${\mathbb {Q}}$
-Cartier Weil divisor on X with
${\mathbb {Q}}$
-Cartier Weil divisor on X with
![]() $h^0(X, D')\geq 2$
. We say that
$h^0(X, D')\geq 2$
. We say that
![]() $|D|$
and
$|D|$
and
![]() $|D'|$
are composed with the same pencil, if both of them are composed with pencils and they define the same fibration structure
$|D'|$
are composed with the same pencil, if both of them are composed with pencils and they define the same fibration structure
![]() $W\to \mathbb {P}^1$
. In particular,
$W\to \mathbb {P}^1$
. In particular,
![]() $|D|$
and
$|D|$
and
![]() $|D'|$
are not composed with the same pencil if one of them is not composed with a pencil.
$|D'|$
are not composed with the same pencil if one of them is not composed with a pencil.
2.2 Reid’s Riemann–Roch formula and Chen–Chen’s method
A basket B is a collection of pairs of coprime integers where a pair is allowed to appear several times, say
For simplicity, we will alternatively write a basket as a set of pairs with weights, say, for example,
Let X be a terminal weak
![]() $\mathbb {Q}$
-Fano threefold. According to Reid [Reference Reid20], there is a basket of (virtual) orbifold points
$\mathbb {Q}$
-Fano threefold. According to Reid [Reference Reid20], there is a basket of (virtual) orbifold points
associated with X, where a pair
![]() $\left (b_{i}, r_{i}\right )$
corresponds to an orbifold point
$\left (b_{i}, r_{i}\right )$
corresponds to an orbifold point
![]() $Q_{i}$
of type
$Q_{i}$
of type
![]() $\frac {1}{r_{i}}\left (1, -1, b_{i}\right )$
. Denote by
$\frac {1}{r_{i}}\left (1, -1, b_{i}\right )$
. Denote by
![]() $\mathcal {R}_X$
the collection of
$\mathcal {R}_X$
the collection of
![]() $r_i$
(counted with multiplicities) appearing in
$r_i$
(counted with multiplicities) appearing in
![]() $B_X$
, and
$B_X$
, and
![]() $r_{\max }=\max \{r_i\mid r_i\in \mathcal {R}_X\}$
. Note that the Cartier index
$r_{\max }=\max \{r_i\mid r_i\in \mathcal {R}_X\}$
. Note that the Cartier index
![]() $r_X$
of
$r_X$
of
![]() $K_X$
is just
$K_X$
is just
![]() ${\text {lcm}}\{r_i\mid r_i\in \mathcal {R}_X\}$
.
${\text {lcm}}\{r_i\mid r_i\in \mathcal {R}_X\}$
.
According to Reid [Reference Reid20], for any positive integer n,
where
![]() $l(n+1)=\sum _{i} \sum _{j=1}^{n} \frac {\overline {j b_{i}}\left (r_{i}-\overline {j b_{i}}\right )}{2 r_{i}}$
and the first sum runs over Reid’s basket of orbifold points. Here,
$l(n+1)=\sum _{i} \sum _{j=1}^{n} \frac {\overline {j b_{i}}\left (r_{i}-\overline {j b_{i}}\right )}{2 r_{i}}$
and the first sum runs over Reid’s basket of orbifold points. Here,
![]() $\overline {jb_i}$
means the smallest nonnegative residue of
$\overline {jb_i}$
means the smallest nonnegative residue of
![]() $jb_i \bmod r_i$
.
$jb_i \bmod r_i$
.
Set
![]() $\sigma (B_X)=\sum _{i}b_{i}$
and
$\sigma (B_X)=\sum _{i}b_{i}$
and
![]() $\sigma '(B_X)=\sum _{i}\frac {b_{i}^{2}}{r_{i}}$
. From (2.1), for
$\sigma '(B_X)=\sum _{i}\frac {b_{i}^{2}}{r_{i}}$
. From (2.1), for
![]() $n=1, 2$
,
$n=1, 2$
,
Denote
 $$ \begin{align*}\gamma(B_X):=\sum_i\frac{1}{r_i}-\sum_ir_i+24. \end{align*} $$
$$ \begin{align*}\gamma(B_X):=\sum_i\frac{1}{r_i}-\sum_ir_i+24. \end{align*} $$
By [Reference Kollár, Miyaoka, Mori and Takagi13] and [Reference Reid20, 10.3],
We recall Chen–Chen’s method on basket packing from [Reference Chen, Chen, Chen and Jiang2]. Let
be a basket and assume that
![]() $b_1r_2-b_2r_1=1$
, then the new basket
$b_1r_2-b_2r_1=1$
, then the new basket
is called a prime packing of B. We say that a basket
![]() $B'$
is dominated by B, denoted by
$B'$
is dominated by B, denoted by
![]() $B\succeq B'$
, if
$B\succeq B'$
, if
![]() $B'$
can be achieved from B by a sequence of prime packings (including the case
$B'$
can be achieved from B by a sequence of prime packings (including the case
![]() $B=B'$
).
$B=B'$
).
By [Reference Chen and Chen2, §2.5], there is a unique basket
![]() $B_{X}^{(0)}$
, called the initial basket of
$B_{X}^{(0)}$
, called the initial basket of
![]() $B_X$
, of the form
$B_X$
, of the form
![]() $B_{X}^{(0)}=\{n_{1, r}^{0}\times (1, r)\mid r\geq 2\}$
such that
$B_{X}^{(0)}=\{n_{1, r}^{0}\times (1, r)\mid r\geq 2\}$
such that
![]() $B_{X}^{(0)}\succeq B_X$
. By [Reference Chen and Chen2, §2.7], we have
$B_{X}^{(0)}\succeq B_X$
. By [Reference Chen and Chen2, §2.7], we have
where
![]() $\sigma _{5}=\sum _{r\geq 5} n_{1, r}^{0}$
. We refer to [Reference Chen, Chen, Chen and Jiang2] for more details.
$\sigma _{5}=\sum _{r\geq 5} n_{1, r}^{0}$
. We refer to [Reference Chen, Chen, Chen and Jiang2] for more details.
2.3 Auxiliary results
We list here some useful results on terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds.
${\mathbb {Q}}$
-Fano threefolds.
Proposition 2.2. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Then:
${\mathbb {Q}}$
-Fano threefold. Then:
-
(1)
 $r_X=840$
or
$r_X=840$
or
 $r_X\leq 660$
[Reference Chen and Jiang5, Prop. 2.4].
$r_X\leq 660$
[Reference Chen and Jiang5, Prop. 2.4]. -
(2)
 $P_{-8}\geq 2$
[Reference Chen and Chen2, Th. 1.1]; moreover, if
$P_{-8}\geq 2$
[Reference Chen and Chen2, Th. 1.1]; moreover, if
 $P_{-1}=0$
and
$P_{-1}=0$
and
 $P_{-2}>0$
, then
$P_{-2}>0$
, then
 $P_{-6}\geq 2$
[Reference Chen and Chen2, Case 1 of Proof of Prop. 3.10].
$P_{-6}\geq 2$
[Reference Chen and Chen2, Case 1 of Proof of Prop. 3.10]. -
(3)
 $-K_X^3\geq \frac {1}{330}$
[Reference Chen and Chen2, Th. 1.1]; moreover, if
$-K_X^3\geq \frac {1}{330}$
[Reference Chen and Chen2, Th. 1.1]; moreover, if
 $P_{-1}=0$
and
$P_{-1}=0$
and
 $P_{-2}>0$
, then
$P_{-2}>0$
, then
 $-K_X^3\geq \frac {1}{70}$
, and if in addition
$-K_X^3\geq \frac {1}{70}$
, and if in addition
 $P_{-4}\geq 2$
, then
$P_{-4}\geq 2$
, then
 $-K_X^3\geq \frac {1}{30}$
[Reference Chen and Chen2, (4.1), Lem. 4.2, and Case I of Proof of Th. 4.4].
$-K_X^3\geq \frac {1}{30}$
[Reference Chen and Chen2, (4.1), Lem. 4.2, and Case I of Proof of Th. 4.4]. -
(4) If
 $P_{-1}=0$
, then
$P_{-1}=0$
, then
 $2\in \mathcal {R}_X$
[Reference Chen and Jiang5, Proof of Th. 1.8, p. 106].
$2\in \mathcal {R}_X$
[Reference Chen and Jiang5, Proof of Th. 1.8, p. 106].
Lemma 2.3. Suppose that
![]() $\{(b_i, r_i)\mid 1\leq i\leq k\}$
is a collection of pairs of integers with
$\{(b_i, r_i)\mid 1\leq i\leq k\}$
is a collection of pairs of integers with
![]() $0<2b_i\leq r_i$
for
$0<2b_i\leq r_i$
for
![]() $1\leq i\leq k$
. Then
$1\leq i\leq k$
. Then
![]() $\sum _{i=1}^k(r_i-\frac {1}{r_i})\geq \frac {3}{2}\sum _{i=1}^kb_i$
.
$\sum _{i=1}^k(r_i-\frac {1}{r_i})\geq \frac {3}{2}\sum _{i=1}^kb_i$
.
Proof.
![]() $r_i\geq 2b_i$
implies that
$r_i\geq 2b_i$
implies that
![]() $r_i-\frac {1}{r_i}\geq \frac {3}{2}b_i$
.
$r_i-\frac {1}{r_i}\geq \frac {3}{2}b_i$
.
3 The criteria for birationality
In this section, we recall the birationality criteria of terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds in [Reference Chen and Jiang5], [Reference Chen and Jiang6]. Here, we remark that all birationality criteria in this section are from [Reference Chen and Jiang5], [Reference Chen and Jiang6] except for Theorem 3.5 and Corollary 3.7 (which are minor generalizations of [Reference Chen and Jiang6, Th. 5.9]). Also, we provide Lemma 3.3 in order to apply Corollary 3.7 efficiently. In fact, in [Reference Chen and Jiang6], [Reference Chen and Jiang6, Th. 5.9] is only used for very special cases, but in this paper, thanks to Lemma 3.3, we make use of Corollary 3.7 in many cases.
${\mathbb {Q}}$
-Fano threefolds in [Reference Chen and Jiang5], [Reference Chen and Jiang6]. Here, we remark that all birationality criteria in this section are from [Reference Chen and Jiang5], [Reference Chen and Jiang6] except for Theorem 3.5 and Corollary 3.7 (which are minor generalizations of [Reference Chen and Jiang6, Th. 5.9]). Also, we provide Lemma 3.3 in order to apply Corollary 3.7 efficiently. In fact, in [Reference Chen and Jiang6], [Reference Chen and Jiang6, Th. 5.9] is only used for very special cases, but in this paper, thanks to Lemma 3.3, we make use of Corollary 3.7 in many cases.
3.1 General settings
We recall numerical invariants needed in the birationality criteria, namely,
![]() $\nu _0$
,
$\nu _0$
,
![]() $m_0$
,
$m_0$
,
![]() $a(m_0)$
,
$a(m_0)$
,
![]() $m_1$
,
$m_1$
,
![]() $\mu ^{\prime }_0$
, and
$\mu ^{\prime }_0$
, and
![]() $N_0$
.
$N_0$
.
Notation 3.1. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold.
${\mathbb {Q}}$
-Fano threefold.
Let
![]() $\nu _{0}$
be a positive integer such that
$\nu _{0}$
be a positive integer such that
![]() $P_{-\nu _{0}}>0$
.
$P_{-\nu _{0}}>0$
.
Take a positive integer
![]() $m_0$
such that
$m_0$
such that
![]() $P_{-m_0}\geq 2$
. Set
$P_{-m_0}\geq 2$
. Set
 $$ \begin{align*}a(m_{0})= \begin{cases}6, & \text{if } m_{0} \geq 2, \\ 1, & \text{if } m_{0}=1.\end{cases} \end{align*} $$
$$ \begin{align*}a(m_{0})= \begin{cases}6, & \text{if } m_{0} \geq 2, \\ 1, & \text{if } m_{0}=1.\end{cases} \end{align*} $$
Take
![]() $m_1\geq m_0$
to be an integer with
$m_1\geq m_0$
to be an integer with
![]() $P_{-m_1}\geq 2$
such that
$P_{-m_1}\geq 2$
such that
![]() $|-m_0K_X|$
and
$|-m_0K_X|$
and
![]() $|-m_1K_X|$
are not composed with the same pencil.
$|-m_1K_X|$
are not composed with the same pencil.
Set
![]() $D:=-m_0K_X$
and keep the same notation as in §2.1. Denote S to be a generic irreducible element of
$D:=-m_0K_X$
and keep the same notation as in §2.1. Denote S to be a generic irreducible element of
![]() $|M_{-m_0}|=\operatorname {Mov}|\lfloor \pi ^*(-m_0K_X)\rfloor |$
. Choose a positive rational number
$|M_{-m_0}|=\operatorname {Mov}|\lfloor \pi ^*(-m_0K_X)\rfloor |$
. Choose a positive rational number
![]() $\mu _{0}'$
such that
$\mu _{0}'$
such that
Set
![]() $N_{0}=r_{X}(\pi ^{*}(-K_{X})^{2} \cdot S)$
.
$N_{0}=r_{X}(\pi ^{*}(-K_{X})^{2} \cdot S)$
.
Remark 3.2 [Reference Chen and Jiang6, Rem. 5.8]
Here, we explain how to choose
![]() $\mu ^{\prime }_0$
. In general, by assumption, we can always take
$\mu ^{\prime }_0$
. In general, by assumption, we can always take
![]() $\mu _{0}'=m_0$
. On the other hand, if
$\mu _{0}'=m_0$
. On the other hand, if
![]() $|-m_{0} K_{X}|$
and
$|-m_{0} K_{X}|$
and
![]() $|-k K_{X}|$
are composed with the same pencil for some positive integer k, and
$|-k K_{X}|$
are composed with the same pencil for some positive integer k, and
![]() $\frac {k}{P_{-k}-1}<m_0$
, then we can take
$\frac {k}{P_{-k}-1}<m_0$
, then we can take
![]() $\mu _{0}'=\frac {k}{P_{-k}-1}$
as
$\mu _{0}'=\frac {k}{P_{-k}-1}$
as
Lemma 3.3. In Notation 3.1,
![]() $N_0\geq \lceil \frac {r_X}{m_1\nu _0 r_{\max }}\rceil $
.
$N_0\geq \lceil \frac {r_X}{m_1\nu _0 r_{\max }}\rceil $
.
Proof. We may modify
![]() $\pi $
such that
$\pi $
such that
![]() $|M_{-m_1}|=\operatorname {Mov}|\lfloor \pi ^*(-m_1K_X)\rfloor |$
is base-point-free. Pick a generic irreducible element C of the base-point-free linear system
$|M_{-m_1}|=\operatorname {Mov}|\lfloor \pi ^*(-m_1K_X)\rfloor |$
is base-point-free. Pick a generic irreducible element C of the base-point-free linear system
![]() $|M_{-m_1}|_S|$
. Since
$|M_{-m_1}|_S|$
. Since
![]() $\pi ^*(-m_1K_X)\geq M_{-m_1}$
,
$\pi ^*(-m_1K_X)\geq M_{-m_1}$
,
![]() $\pi ^*(-m_1K_X)|_S\geq C.$
Set
$\pi ^*(-m_1K_X)|_S\geq C.$
Set
By [Reference Chen and Jiang5, Prop. 5.7(v)],
![]() $\zeta \geq \frac {1}{\nu _0 r_{\max }}$
. Since
$\zeta \geq \frac {1}{\nu _0 r_{\max }}$
. Since
![]() $\pi ^*(-K_X)|_S$
is nef,
$\pi ^*(-K_X)|_S$
is nef,
 $$ \begin{align*}\pi^{*}(-K_{X})^{2} \cdot S\geq\pi^*(-K_X)|_S\cdot\frac{1}{m_1}C\geq \frac{1}{m_1\nu_0 r_{\max}}.\end{align*} $$
$$ \begin{align*}\pi^{*}(-K_{X})^{2} \cdot S\geq\pi^*(-K_X)|_S\cdot\frac{1}{m_1}C\geq \frac{1}{m_1\nu_0 r_{\max}}.\end{align*} $$
Hence,
![]() $N_0\geq \lceil \frac {r_X}{m_1\nu _0 r_{\max }}\rceil $
as
$N_0\geq \lceil \frac {r_X}{m_1\nu _0 r_{\max }}\rceil $
as
![]() $N_0$
is an integer by [Reference Chen and Jiang5, Lem. 4.1].
$N_0$
is an integer by [Reference Chen and Jiang5, Lem. 4.1].
3.2 Birationality criteria
We recall the birationality criteria of terminal weak
![]() $\mathbb {Q}$
-Fano threefolds.
$\mathbb {Q}$
-Fano threefolds.
Theorem 3.4 [Reference Chen and Jiang5, Th. 5.11]
Keep the setting in Notation 3.1. Then the mth anti-canonical map
![]() $\varphi _{-m}$
is birational if one of the following conditions holds:
$\varphi _{-m}$
is birational if one of the following conditions holds:
-
(1)
 $m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor 3\mu ^{\prime }_{0}\rfloor +3 m_{1}\}.$
$m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor 3\mu ^{\prime }_{0}\rfloor +3 m_{1}\}.$
-
(2)
 $m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor \frac {5}{3}\mu ^{\prime }_{0}+\frac {5}{3}m_{1}\rfloor , \lfloor \mu ^{\prime }_{0}\rfloor +m_{1}+2 r_{\max }\}.$
$m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor \frac {5}{3}\mu ^{\prime }_{0}+\frac {5}{3}m_{1}\rfloor , \lfloor \mu ^{\prime }_{0}\rfloor +m_{1}+2 r_{\max }\}.$
-
(3)
 $m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor \mu ^{\prime }_{0}\rfloor +m_{1}+2 \nu _0r_{\max }\}.$
$m \geq \max \{m_{0}+m_{1}+a(m_{0}), \lfloor \mu ^{\prime }_{0}\rfloor +m_{1}+2 \nu _0r_{\max }\}.$
As another criterion, we have the following modification of [Reference Chen and Jiang6, Th. 5.9].
Theorem 3.5. Keep the setting in Notation 3.1. Fix a real number
![]() $\beta \geq 8$
. Then the mth anti-canonical map
$\beta \geq 8$
. Then the mth anti-canonical map
![]() $\varphi _{-m}$
is birational if
$\varphi _{-m}$
is birational if
 $$ \begin{align*}m \geq \max\left\{m_{0}+a(m_{0}), \left\lceil\mu_{0}'+\frac{4 \nu_{0} r_{\max }}{1+\sqrt{1-\frac{8}{\beta}}}\right\rceil-1, \lfloor\mu_{0}'+\sqrt{{\beta r_{X}}/{N_0} }\rfloor\right\}. \end{align*} $$
$$ \begin{align*}m \geq \max\left\{m_{0}+a(m_{0}), \left\lceil\mu_{0}'+\frac{4 \nu_{0} r_{\max }}{1+\sqrt{1-\frac{8}{\beta}}}\right\rceil-1, \lfloor\mu_{0}'+\sqrt{{\beta r_{X}}/{N_0} }\rfloor\right\}. \end{align*} $$
Proof. The proof is the same as [Reference Chen and Jiang6, Th. 5.9] by replacing [Reference Chen and Jiang6, Lem. 5.10] with Lemma 3.6.
Lemma 3.6 [Reference Chen, Chen, Chen and Jiang3, Th. 2.8]
Let S be a smooth projective surface, and let L be a nef and big
![]() ${\mathbb {Q}}$
-divisor on S satisfying the following conditions:
${\mathbb {Q}}$
-divisor on S satisfying the following conditions:
-
(1)
 $L^{2}>\beta $
, for some real number
$L^{2}>\beta $
, for some real number
 $\beta \geq 8$
, and
$\beta \geq 8$
, and -
(2)
 $(L \cdot C_{P}) \geq \frac {4}{1+\sqrt {1-\frac {8}{\beta }}}$
for all irreducible curves
$(L \cdot C_{P}) \geq \frac {4}{1+\sqrt {1-\frac {8}{\beta }}}$
for all irreducible curves
 $C_{P}$
passing through any very general point
$C_{P}$
passing through any very general point
 $P \in S$
.
$P \in S$
.
Then the linear system
![]() $|K_{S}+\lceil L\rceil |$
separates two distinct points in very general positions. Consequently,
$|K_{S}+\lceil L\rceil |$
separates two distinct points in very general positions. Consequently,
![]() $|K_{S}+\lceil L\rceil |$
gives a birational map.
$|K_{S}+\lceil L\rceil |$
gives a birational map.
We will use the following version of Theorem 3.5.
Corollary 3.7. Keep the setting in Notation 3.1. Then the mth anti-canonical map
![]() $\varphi _{-m}$
is birational if one of the following conditions holds:
$\varphi _{-m}$
is birational if one of the following conditions holds:
-
(1)
 $m \geq \max \{m_{0}+a(m_{0}), \lceil \mu _{0}'\rceil +4 \nu _{0} r_{\max }-1, \lfloor \mu _{0}'+\sqrt {{8r_{X}}/{N_0} }\rfloor \}.$
$m \geq \max \{m_{0}+a(m_{0}), \lceil \mu _{0}'\rceil +4 \nu _{0} r_{\max }-1, \lfloor \mu _{0}'+\sqrt {{8r_{X}}/{N_0} }\rfloor \}.$
-
(2)
 $\nu _0 r_{\max }\geq \sqrt {\frac {r_{X}}{2N_0}}$
and
$\nu _0 r_{\max }\geq \sqrt {\frac {r_{X}}{2N_0}}$
and  $$ \begin{align*}m \geq \max\left\{m_{0}+a(m_{0}), \left\lfloor\mu_{0}'+2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}\right\rfloor\right\}. \end{align*} $$
$$ \begin{align*}m \geq \max\left\{m_{0}+a(m_{0}), \left\lfloor\mu_{0}'+2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}\right\rfloor\right\}. \end{align*} $$
Proof. (1) follows directly from [Reference Chen and Jiang6, Th. 5.9] or Theorem 3.5 with
![]() $\beta =8$
. For (2), take
$\beta =8$
. For (2), take
 $$ \begin{align*}\beta=\frac{N_0}{r_{X}}\left(2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}\right)^2\geq 8\end{align*} $$
$$ \begin{align*}\beta=\frac{N_0}{r_{X}}\left(2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}\right)^2\geq 8\end{align*} $$
in Theorem 3.5. Then
 $$ \begin{align*} \frac{4 \nu_{0} r_{\max }}{1+\sqrt{1-\frac{8}{\beta}}} ={}&\frac{4 \nu_{0} r_{\max }\sqrt{\beta}}{\sqrt{\beta}+\sqrt{\beta-8}}\\ ={}&\frac{4 \nu_{0} r_{\max }\sqrt{\beta}}{\sqrt{\frac{N_0}{r_{X}}}\left(2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}+\left|2\nu_0 r_{\max}-\frac{r_X}{N_0 \nu_0 r_{\max}}\right|\right)}\\ ={}&\sqrt{{\beta r_{X}}/{N_0}}. \end{align*} $$
$$ \begin{align*} \frac{4 \nu_{0} r_{\max }}{1+\sqrt{1-\frac{8}{\beta}}} ={}&\frac{4 \nu_{0} r_{\max }\sqrt{\beta}}{\sqrt{\beta}+\sqrt{\beta-8}}\\ ={}&\frac{4 \nu_{0} r_{\max }\sqrt{\beta}}{\sqrt{\frac{N_0}{r_{X}}}\left(2\nu_0 r_{\max}+\frac{r_X}{N_0 \nu_0 r_{\max}}+\left|2\nu_0 r_{\max}-\frac{r_X}{N_0 \nu_0 r_{\max}}\right|\right)}\\ ={}&\sqrt{{\beta r_{X}}/{N_0}}. \end{align*} $$
So the conclusion follows from Theorem 3.5.
Finally, we explain the strategy to apply the birationality criteria to assert the birationality. It is clear that in order to apply Theorem 3.4 and Corollary 3.7, we need to control the values of (some of)
![]() $\nu _0$
,
$\nu _0$
,
![]() $m_0$
,
$m_0$
,
![]() $m_1$
,
$m_1$
,
![]() $\mu ^{\prime }_0$
,
$\mu ^{\prime }_0$
,
![]() $N_0$
, and
$N_0$
, and
![]() $r_X, r_{\max }$
. To be more precise, we need to give upper bounds of
$r_X, r_{\max }$
. To be more precise, we need to give upper bounds of
![]() $\nu _0$
,
$\nu _0$
,
![]() $m_0$
,
$m_0$
,
![]() $m_1$
,
$m_1$
,
![]() $\mu ^{\prime }_0$
,
$\mu ^{\prime }_0$
,
![]() $r_X$
,
$r_X$
,
![]() $r_{\max }$
and lower bounds of
$r_{\max }$
and lower bounds of
![]() $N_0$
. Here,
$N_0$
. Here,
![]() $m_0$
and
$m_0$
and
![]() $\nu _0$
can be controlled by Proposition 2.2 (in particular, we can always take
$\nu _0$
can be controlled by Proposition 2.2 (in particular, we can always take
![]() $m_0=8$
),
$m_0=8$
),
![]() $\mu ^{\prime }_0$
can be controlled by Remark 3.2,
$\mu ^{\prime }_0$
can be controlled by Remark 3.2,
![]() $N_0$
can be controlled by Lemma 3.3 (in most cases, we use the trivial lower bound
$N_0$
can be controlled by Lemma 3.3 (in most cases, we use the trivial lower bound
![]() $N_0\geq 1$
), and
$N_0\geq 1$
), and
![]() $r_X$
and
$r_X$
and
![]() $r_{\max }$
can be controlled by (2.4). So the most important and difficult part is to bound
$r_{\max }$
can be controlled by (2.4). So the most important and difficult part is to bound
![]() $m_1$
. We will deal with this issue in the next section.
$m_1$
. We will deal with this issue in the next section.
4 A new criterion for
 $|-mK|$
not composed with a pencil
$|-mK|$
not composed with a pencil
In this section, we give a new criterion on when
![]() $|-mK_X|$
is not composed with a pencil for a terminal weak
$|-mK_X|$
is not composed with a pencil for a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold X. Such a criterion is essential in order to apply criteria for birationality in §3 (see also [Reference Chen4]–[Reference Chen and Jiang6]). In [Reference Chen and Jiang5], the following proposition is used to determine when
${\mathbb {Q}}$
-Fano threefold X. Such a criterion is essential in order to apply criteria for birationality in §3 (see also [Reference Chen4]–[Reference Chen and Jiang6]). In [Reference Chen and Jiang5], the following proposition is used to determine when
![]() $|-mK|$
is not composed with a pencil.
$|-mK|$
is not composed with a pencil.
Proposition 4.1 [Reference Chen and Jiang5, Cor. 4.2]
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
for some positive integer m, then
![]() $|-m K_X|$
is not composed with a pencil.
$|-m K_X|$
is not composed with a pencil.
However, Proposition 4.1 is too weak for application, especially when
![]() $r_X(-K_X^3)$
is large (see Example 4.10). In [Reference Chen and Jiang6], there is a modification of this inequality (cf. [Reference Chen and Jiang6, Lem. 4.2 and Prop. 5.2]), but one has to replace X with a birational model. In this paper, by technique developed recently in [Reference Jiang and Zou12], we give a new criterion.
$r_X(-K_X^3)$
is large (see Example 4.10). In [Reference Chen and Jiang6], there is a modification of this inequality (cf. [Reference Chen and Jiang6, Lem. 4.2 and Prop. 5.2]), but one has to replace X with a birational model. In this paper, by technique developed recently in [Reference Jiang and Zou12], we give a new criterion.
Theorem 4.2. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
for some positive integer m, then
![]() $|-mK_X|$
is not composed with a pencil.
$|-mK_X|$
is not composed with a pencil.
4.1 A structure theorem of terminal weak
 ${\mathbb {Q}}$
-Fano threefolds
${\mathbb {Q}}$
-Fano threefolds
We recall the following structure theorem of terminal weak
![]() ${\mathbb {Q}}$
-Fano threefolds from [Reference Jiang and Zou12]. It plays the role of Fano–Mori triples as in [Reference Chen and Jiang6]. Unlike [Reference Chen and Jiang6], we do not need to replace by a birational model (cf. [Reference Chen and Jiang6, Prop. 3.9]).
${\mathbb {Q}}$
-Fano threefolds from [Reference Jiang and Zou12]. It plays the role of Fano–Mori triples as in [Reference Chen and Jiang6]. Unlike [Reference Chen and Jiang6], we do not need to replace by a birational model (cf. [Reference Chen and Jiang6, Prop. 3.9]).
Proposition 4.3 [Reference Jiang and Zou12, Prop. 4.1]
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Then there exists a normal projective threefold Y birational to X satisfying the following properties:
${\mathbb {Q}}$
-Fano threefold. Then there exists a normal projective threefold Y birational to X satisfying the following properties:
-
(1) Y is
 $\mathbb {Q}$
-factorial terminal.
$\mathbb {Q}$
-factorial terminal. -
(2)
 $-K_Y$
is big.
$-K_Y$
is big. -
(3) For any sufficiently large and divisible positive integer n,
 $|-nK_Y|$
is movable.
$|-nK_Y|$
is movable. -
(4) For a general member
 $M\in |-nK_Y|$
, M is irreducible and
$M\in |-nK_Y|$
, M is irreducible and
 $(Y, \frac {1}{n}M)$
is canonical.
$(Y, \frac {1}{n}M)$
is canonical. -
(5) There exists a projective morphism
 $g: Y\to S$
with connected fibers where F is a general fiber of g, such that one of the following conditions holds:
$g: Y\to S$
with connected fibers where F is a general fiber of g, such that one of the following conditions holds:-
(a) S is a point and Y is a
 ${\mathbb {Q}}$
-Fano threefold with
${\mathbb {Q}}$
-Fano threefold with
 $\rho (Y)=1$
.
$\rho (Y)=1$
. -
(b)
 $S= \mathbb {P}^1$
and F is a smooth weak del Pezzo surface.
$S= \mathbb {P}^1$
and F is a smooth weak del Pezzo surface. -
(c) S is a del Pezzo surface with at worst Du Val singularities and
 $\rho (S)=1$
, and
$\rho (S)=1$
, and
 $F\simeq \mathbb {P}^1$
.
$F\simeq \mathbb {P}^1$
.
-
Here, we remark that in the proof of [Reference Jiang and Zou12, Prop. 4.1], Y is obtained by running a K-MMP on a
![]() ${\mathbb {Q}}$
-factorialization of X, so the induced map
${\mathbb {Q}}$
-factorialization of X, so the induced map
![]() $X\dashrightarrow Y$
is a contraction, that is, it does not extract any divisor.
$X\dashrightarrow Y$
is a contraction, that is, it does not extract any divisor.
4.2 Bounding coefficients of anti-canonical divisors
In this subsection, we discuss coefficients of certain divisors in the
![]() $\mathbb {Q}$
-linear system of the anti-canonical divisor in several cases.
$\mathbb {Q}$
-linear system of the anti-canonical divisor in several cases.
Lemma 4.4. Let S be a smooth weak del Pezzo surface, and let C be a nonzero effective integral divisor on S which is movable. If
![]() $-K_S\sim _{{\mathbb {Q}}}aC+B$
for some positive rational number a and some effective
$-K_S\sim _{{\mathbb {Q}}}aC+B$
for some positive rational number a and some effective
![]() ${\mathbb {Q}}$
-divisor B, then
${\mathbb {Q}}$
-divisor B, then
![]() $a\leq 4$
.
$a\leq 4$
.
Proof. By classical surface theory, it is well known that there is a birational map from S to
![]() $\mathbb {P}^2$
or the Hirzebruch surface
$\mathbb {P}^2$
or the Hirzebruch surface
![]() $\mathbb {F}_0$
or
$\mathbb {F}_0$
or
![]() $\mathbb {F}_2$
. So, by taking pushforward, we may replace S by
$\mathbb {F}_2$
. So, by taking pushforward, we may replace S by
![]() $\mathbb {P}^2$
or
$\mathbb {P}^2$
or
![]() $\mathbb {F}_0$
or
$\mathbb {F}_0$
or
![]() $\mathbb {F}_2$
. Here, C is not contracted by the pushforward as it is movable.
$\mathbb {F}_2$
. Here, C is not contracted by the pushforward as it is movable.
If
![]() $S=\mathbb {P}^2$
, then intersecting with a general line L, we get
$S=\mathbb {P}^2$
, then intersecting with a general line L, we get
![]() $a\leq a(C\cdot L)\leq (-K_S\cdot L)=3$
.
$a\leq a(C\cdot L)\leq (-K_S\cdot L)=3$
.
If
![]() $S=\mathbb {F}_0$
, then we may find a ruling structure
$S=\mathbb {F}_0$
, then we may find a ruling structure
![]() $\phi : \mathbb {F}_0\to \mathbb {P}^1$
such that C is not vertical. Then we get
$\phi : \mathbb {F}_0\to \mathbb {P}^1$
such that C is not vertical. Then we get
![]() $a\leq 2$
by intersecting with a fiber of
$a\leq 2$
by intersecting with a fiber of
![]() $\phi $
.
$\phi $
.
If
![]() $S=\mathbb {F}_2$
, then we consider the natural ruling structure
$S=\mathbb {F}_2$
, then we consider the natural ruling structure
![]() $\phi : \mathbb {F}_2\to \mathbb {P}^1$
. If C is not vertical, then intersecting with a fiber of
$\phi : \mathbb {F}_2\to \mathbb {P}^1$
. If C is not vertical, then intersecting with a fiber of
![]() $\phi $
, we get
$\phi $
, we get
![]() $a\leq 2$
. If C is vertical, then intersecting with
$a\leq 2$
. If C is vertical, then intersecting with
![]() $-K_S$
, we get
$-K_S$
, we get
![]() $a(-K_S\cdot C)\leq K_S^2$
which implies that
$a(-K_S\cdot C)\leq K_S^2$
which implies that
![]() $a\leq 4$
.
$a\leq 4$
.
Lemma 4.5. Let Y be a
![]() $\mathbb {Q}$
-factorial terminal
$\mathbb {Q}$
-factorial terminal
![]() ${\mathbb {Q}}$
-Fano threefold with
${\mathbb {Q}}$
-Fano threefold with
![]() $\rho (Y)=1$
, and let D be an integral divisor with
$\rho (Y)=1$
, and let D be an integral divisor with
![]() $h^0(D)\geq 2$
. If
$h^0(D)\geq 2$
. If
![]() $-K_Y\sim _{{\mathbb {Q}}}aD+B$
for some positive rational number a and some effective
$-K_Y\sim _{{\mathbb {Q}}}aD+B$
for some positive rational number a and some effective
![]() ${\mathbb {Q}}$
-divisor B, then
${\mathbb {Q}}$
-divisor B, then
![]() $a\leq 7$
. Moreover, the equality holds if and only if
$a\leq 7$
. Moreover, the equality holds if and only if
![]() $Y\simeq \mathbb {P}(1, 1, 2, 3)$
,
$Y\simeq \mathbb {P}(1, 1, 2, 3)$
,
![]() $B=0$
, and
$B=0$
, and
![]() $\mathcal {O}_Y(D)\simeq \mathcal {O}_{Y}(1)$
.
$\mathcal {O}_Y(D)\simeq \mathcal {O}_{Y}(1)$
.
Proof. Suppose that
![]() $a\geq 7$
. As
$a\geq 7$
. As
![]() $\rho (Y)=1$
, we have
$\rho (Y)=1$
, we have
![]() $-K_Y\sim _{{\mathbb {Q}}}tD$
for some rational number
$-K_Y\sim _{{\mathbb {Q}}}tD$
for some rational number
![]() $t\geq a \geq 7$
. Recall that the
$t\geq a \geq 7$
. Recall that the
![]() $\mathbb {Q}$
-Fano index of Y is defined by
$\mathbb {Q}$
-Fano index of Y is defined by
By [Reference Prokhorov18, Cor. 3.4(ii)],
![]() $t=q{\mathbb {Q}}(Y)\geq 7$
. As
$t=q{\mathbb {Q}}(Y)\geq 7$
. As
![]() $h^0(D)\geq 2$
, there are two different effective divisors
$h^0(D)\geq 2$
, there are two different effective divisors
![]() $D_1, D_2\in |D|$
such that
$D_1, D_2\in |D|$
such that
![]() $-K_Y\sim _{{\mathbb {Q}}}tD_1\sim _{{\mathbb {Q}}}tD_2$
, which implies that
$-K_Y\sim _{{\mathbb {Q}}}tD_1\sim _{{\mathbb {Q}}}tD_2$
, which implies that
![]() $Y\simeq \mathbb {P}(1, 1, 2, 3)$
by [Reference Prokhorov18, Th. 1.4(vi)]. But, in this case,
$Y\simeq \mathbb {P}(1, 1, 2, 3)$
by [Reference Prokhorov18, Th. 1.4(vi)]. But, in this case,
![]() $t=q{\mathbb {Q}}(Y)=7$
. Hence,
$t=q{\mathbb {Q}}(Y)=7$
. Hence,
![]() $a=7$
,
$a=7$
,
![]() $B=0$
, and
$B=0$
, and
![]() $\mathcal {O}_Y(D)\simeq \mathcal {O}_{Y}(1)$
.
$\mathcal {O}_Y(D)\simeq \mathcal {O}_{Y}(1)$
.
Lemma 4.6. Keep the setting in Proposition 4.3, and suppose that
![]() $S=\mathbb {P}^1$
. If
$S=\mathbb {P}^1$
. If
![]() $-K_Y\sim _{{\mathbb {Q}}}\omega F+E$
for some positive rational number
$-K_Y\sim _{{\mathbb {Q}}}\omega F+E$
for some positive rational number
![]() $\omega $
and some effective
$\omega $
and some effective
![]() ${\mathbb {Q}}$
-divisor E, then
${\mathbb {Q}}$
-divisor E, then
![]() $\omega \leq 12.$
$\omega \leq 12.$
This lemma is from the proof of [Reference Jiang and Zou12, Prop. 4.2]. For the reader’s convenience, we recall the proof here.
Proof. We may assume that
![]() $\omega>2$
. By Proposition 4.3(3)(4), for a sufficiently large and divisible integer n,
$\omega>2$
. By Proposition 4.3(3)(4), for a sufficiently large and divisible integer n,
![]() $|-nK_Y|$
is movable, and there exists an effective
$|-nK_Y|$
is movable, and there exists an effective
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $M\sim -nK_Y$
such that
$M\sim -nK_Y$
such that
![]() $(Y, \frac {1}{n}M)$
is canonical. Since
$(Y, \frac {1}{n}M)$
is canonical. Since
![]() $-K_Y$
is big, we can write
$-K_Y$
is big, we can write
![]() $-K_Y\sim _{{\mathbb {Q}}}A+N$
, where A is an ample
$-K_Y\sim _{{\mathbb {Q}}}A+N$
, where A is an ample
![]() ${\mathbb {Q}}$
-divisor and N is an effective
${\mathbb {Q}}$
-divisor and N is an effective
![]() ${\mathbb {Q}}$
-divisor. Set
${\mathbb {Q}}$
-divisor. Set
![]() $B_{\epsilon }=\frac {1-\epsilon }{n}M+\epsilon N$
for a rational number
$B_{\epsilon }=\frac {1-\epsilon }{n}M+\epsilon N$
for a rational number
![]() $0<\epsilon <1$
. Take two general fibers
$0<\epsilon <1$
. Take two general fibers
![]() $F_1, F_2$
of g. Denote
$F_1, F_2$
of g. Denote
Then
 $$ \begin{align*}-(K_Y+\Delta)\sim_{{\mathbb{Q}}}-\left(1-\frac{2}{\omega}\right)(K_Y+B_{\epsilon})\sim_{{\mathbb{Q}}}\left(1-\frac{2}{\omega}\right)\epsilon A \end{align*} $$
$$ \begin{align*}-(K_Y+\Delta)\sim_{{\mathbb{Q}}}-\left(1-\frac{2}{\omega}\right)(K_Y+B_{\epsilon})\sim_{{\mathbb{Q}}}\left(1-\frac{2}{\omega}\right)\epsilon A \end{align*} $$
is ample as
![]() $\omega>2$
. Hence, by the connectedness lemma [Reference Jiang and Zou12, Lem. 2.6],
$\omega>2$
. Hence, by the connectedness lemma [Reference Jiang and Zou12, Lem. 2.6],
![]() $\operatorname {Nklt}(Y, \Delta )$
is connected. By construction,
$\operatorname {Nklt}(Y, \Delta )$
is connected. By construction,
![]() $F_1\cup F_2\subset \operatorname {Nklt}(Y, \Delta )$
, then
$F_1\cup F_2\subset \operatorname {Nklt}(Y, \Delta )$
, then
![]() $\operatorname {Nklt}(Y, \Delta )$
dominates
$\operatorname {Nklt}(Y, \Delta )$
dominates
![]() $\mathbb {P}^1$
. By the inversion of adjunction [Reference Kollár and Mori14, Lem. 5.50],
$\mathbb {P}^1$
. By the inversion of adjunction [Reference Kollár and Mori14, Lem. 5.50],
![]() $(F, (1-\frac {2}{\omega })B_{\epsilon }|_F+\frac {2}{\omega }E|_F)$
is not klt for a general fiber F of g. As being klt is an open condition on the coefficients, by the arbitrariness of
$(F, (1-\frac {2}{\omega })B_{\epsilon }|_F+\frac {2}{\omega }E|_F)$
is not klt for a general fiber F of g. As being klt is an open condition on the coefficients, by the arbitrariness of
![]() $\epsilon $
, it follows that
$\epsilon $
, it follows that
![]() $(F, (1-\frac {2}{\omega })\frac {1}{n}M|_F+\frac {2}{\omega }E|_F)$
is not klt for a very general fiber F of g.
$(F, (1-\frac {2}{\omega })\frac {1}{n}M|_F+\frac {2}{\omega }E|_F)$
is not klt for a very general fiber F of g.
On the other hand, as
![]() $(Y, \frac {1}{n}M)$
is canonical,
$(Y, \frac {1}{n}M)$
is canonical,
![]() $(F, \frac {1}{n}M|_F)$
is canonical by Bertini’s theorem (see [Reference Kollár and Mori14, Lem. 5.17]). Since M is a general member of a movable linear system by assumption,
$(F, \frac {1}{n}M|_F)$
is canonical by Bertini’s theorem (see [Reference Kollár and Mori14, Lem. 5.17]). Since M is a general member of a movable linear system by assumption,
![]() $M|_F$
is a general member of a movable linear system on F. So each irreducible component of
$M|_F$
is a general member of a movable linear system on F. So each irreducible component of
![]() $M|_F$
is nef. Also, we can take M such that
$M|_F$
is nef. Also, we can take M such that
![]() $M|_F$
and
$M|_F$
and
![]() $E|_F$
have no common irreducible component. By construction,
$E|_F$
have no common irreducible component. By construction,
![]() $\frac {1}{n}M|_F\sim _{\mathbb {Q}} E|_F\sim _{\mathbb {Q}} -K_F$
. So we can apply [Reference Jiang and Zou12, Th. 3.3] to
$\frac {1}{n}M|_F\sim _{\mathbb {Q}} E|_F\sim _{\mathbb {Q}} -K_F$
. So we can apply [Reference Jiang and Zou12, Th. 3.3] to
![]() $F, \frac {1}{n}M|_F, E|_F$
, which implies that
$F, \frac {1}{n}M|_F, E|_F$
, which implies that
![]() $ \frac {2}{\omega }\geq \frac {1}{6}.$
Hence,
$ \frac {2}{\omega }\geq \frac {1}{6}.$
Hence,
![]() $\omega \leq 12$
.
$\omega \leq 12$
.
Lemma 4.7. Keep the setting in Proposition 4.3, and suppose that S is a del Pezzo surface. Suppose that D is a nonzero effective integral divisor on Y which is movable. If
![]() $-K_Y\sim _{{\mathbb {Q}}}\omega D+E$
for some positive rational number
$-K_Y\sim _{{\mathbb {Q}}}\omega D+E$
for some positive rational number
![]() $\omega $
and some effective
$\omega $
and some effective
![]() ${\mathbb {Q}}$
-divisor E, then
${\mathbb {Q}}$
-divisor E, then
![]() $\omega \leq 12.$
$\omega \leq 12.$
Proof. As S is a del Pezzo surface with at worst Du Val singularities and
![]() $\rho (S)=1$
, there are three cases (see [Reference Miyanishi and Zhang15], [Reference Prokhorov17, Rem. 3.4(ii)]):
$\rho (S)=1$
, there are three cases (see [Reference Miyanishi and Zhang15], [Reference Prokhorov17, Rem. 3.4(ii)]):
-
(1)
 $K_{S}^2=9$
and
$K_{S}^2=9$
and
 $S\simeq \mathbb {P}^2$
.
$S\simeq \mathbb {P}^2$
. -
(2)
 $K_{S}^2=8$
and
$K_{S}^2=8$
and
 $S\simeq \mathbb {P}(1, 1, 2)$
.
$S\simeq \mathbb {P}(1, 1, 2)$
. -
(3)
 $1\leq K_{S}^2\leq 6$
.
$1\leq K_{S}^2\leq 6$
.
Consider the linear system
![]() $\mathcal {H}$
on S defined by
$\mathcal {H}$
on S defined by
 $$ \begin{align*}\mathcal{H}:= \begin{cases} |\mathcal{O}_{\mathbb{P}^2}(1)|, & \text{if } S\simeq \mathbb{P}^2,\\ |\mathcal{O}_{\mathbb{P}(1, 1, 2)}(2)|, & \text{if } S\simeq \mathbb{P}(1, 1, 2),\\ |-K_{S}|,& \text{if } 2\leq K_{S}^2\leq 6,\\ |-2K_{S}|,& \text{if } K_{S}^2=1. \end{cases} \end{align*} $$
$$ \begin{align*}\mathcal{H}:= \begin{cases} |\mathcal{O}_{\mathbb{P}^2}(1)|, & \text{if } S\simeq \mathbb{P}^2,\\ |\mathcal{O}_{\mathbb{P}(1, 1, 2)}(2)|, & \text{if } S\simeq \mathbb{P}(1, 1, 2),\\ |-K_{S}|,& \text{if } 2\leq K_{S}^2\leq 6,\\ |-2K_{S}|,& \text{if } K_{S}^2=1. \end{cases} \end{align*} $$
Then
![]() $\mathcal {H}$
is base-point-free and defines a generically finite map (cf. [Reference Dolgachev7, Th. 8.3.2]). By Bertini’s theorem, we can take a general element
$\mathcal {H}$
is base-point-free and defines a generically finite map (cf. [Reference Dolgachev7, Th. 8.3.2]). By Bertini’s theorem, we can take a general element
![]() $H\in \mathcal {H}$
such that H and
$H\in \mathcal {H}$
such that H and
![]() $G=g^{-1}(H)=g^*H$
are smooth. Note that for a general fiber C of
$G=g^{-1}(H)=g^*H$
are smooth. Note that for a general fiber C of
![]() $g|_G$
,
$g|_G$
,
![]() $C\simeq \mathbb {P}^1$
,
$C\simeq \mathbb {P}^1$
,
![]() $(-K_G\cdot C)=2$
, and
$(-K_G\cdot C)=2$
, and
![]() $G|_G\sim (H^2)\cdot C$
.
$G|_G\sim (H^2)\cdot C$
.
Note that
![]() $g|_G$
is factored through by a ruled surface over H, so
$g|_G$
is factored through by a ruled surface over H, so
![]() $K_G^2\leq 8-8g(H)$
. Then
$K_G^2\leq 8-8g(H)$
. Then
 $$ \begin{align*} (-K_Y|_G)^2={}&(-K_{G}+G|_G)^2\\={}&K_{G}^2+4H^2\\\leq{}& 8-8g(H)+4H^2\\={}&-4(K_{S}\cdot H)\leq24. \end{align*} $$
$$ \begin{align*} (-K_Y|_G)^2={}&(-K_{G}+G|_G)^2\\={}&K_{G}^2+4H^2\\\leq{}& 8-8g(H)+4H^2\\={}&-4(K_{S}\cdot H)\leq24. \end{align*} $$
By construction, as
![]() $|G|$
defines a morphism from Y to a surface and D is movable,
$|G|$
defines a morphism from Y to a surface and D is movable,
![]() $D|_G$
is an effective nonzero integral divisor for a general G. So we may write
$D|_G$
is an effective nonzero integral divisor for a general G. So we may write
Take a general fiber C of
![]() $g|_G$
. If
$g|_G$
. If
![]() $(D|_G \cdot C)\neq 0$
, then by (4.1) intersecting with C,
$(D|_G \cdot C)\neq 0$
, then by (4.1) intersecting with C,
![]() $\omega \leq 2$
. If
$\omega \leq 2$
. If
![]() $(D|_G \cdot C)=0$
, then
$(D|_G \cdot C)=0$
, then
![]() $D|_G $
is vertical over H and thus
$D|_G $
is vertical over H and thus
![]() $D|_G$
is numerically equivalent to a multiple of C. By Proposition 4.3(3),
$D|_G$
is numerically equivalent to a multiple of C. By Proposition 4.3(3),
![]() $-K_Y|_G$
is nef. Then, by (4.1), intersecting with
$-K_Y|_G$
is nef. Then, by (4.1), intersecting with
![]() $-K_Y|_G$
,
$-K_Y|_G$
,
which implies that
![]() $\omega \leq 12$
.
$\omega \leq 12$
.
4.3 A new geometric inequality
Now, we are prepared to prove Theorem 4.2.
Proof of Theorem 4.2
It suffices to show that, if
![]() $|-mK_X|$
is composed with a pencil, then
$|-mK_X|$
is composed with a pencil, then
![]() $ P_{-m}\leq 12m+1. $
$ P_{-m}\leq 12m+1. $
Take
![]() $g: Y\to S$
to be the morphism in Proposition 4.3. Take a common resolution
$g: Y\to S$
to be the morphism in Proposition 4.3. Take a common resolution
![]() $\pi :W\to X$
,
$\pi :W\to X$
,
![]() $q:W\to Y$
. We may modify
$q:W\to Y$
. We may modify
![]() $\pi $
such that
$\pi $
such that
![]() $f: W\to \mathbb {P}^1$
is the fibration induced by
$f: W\to \mathbb {P}^1$
is the fibration induced by
![]() $|-mK_X|$
as in §2.1. See the following diagram:
$|-mK_X|$
as in §2.1. See the following diagram:

Denote by
![]() $F_W$
a general fiber of f. Then
$F_W$
a general fiber of f. Then
where E is an effective
![]() ${\mathbb {Q}}$
-divisor on W. Set
${\mathbb {Q}}$
-divisor on W. Set
![]() $\omega =\frac {P_{-m}-1}{m}$
. Pushing forward (4.2) to Y, we have
$\omega =\frac {P_{-m}-1}{m}$
. Pushing forward (4.2) to Y, we have
where
![]() $E_Y$
is an effective
$E_Y$
is an effective
![]() ${\mathbb {Q}}$
-divisor on Y. Note that
${\mathbb {Q}}$
-divisor on Y. Note that
![]() $q_{*}F_W$
is a general member of a movable linear system.
$q_{*}F_W$
is a general member of a movable linear system.
Case 1. S is a point.
In this case,
![]() $\omega \leq 7$
by (4.3) and Lemma 4.5.
$\omega \leq 7$
by (4.3) and Lemma 4.5.
Case 2.
![]() $S=\mathbb {P}^1$
.
$S=\mathbb {P}^1$
.
If
![]() $S=\mathbb {P}^1$
and
$S=\mathbb {P}^1$
and
![]() $q_{*}F_W|_F=0$
, then
$q_{*}F_W|_F=0$
, then
![]() $q_{*}F_W \sim F$
and
$q_{*}F_W \sim F$
and
![]() $-K_Y\sim _{{\mathbb {Q}}}\omega F+E_Y$
. By Lemma 4.6,
$-K_Y\sim _{{\mathbb {Q}}}\omega F+E_Y$
. By Lemma 4.6,
![]() $\omega \leq 12$
.
$\omega \leq 12$
.
If
![]() $S=\mathbb {P}^1$
and
$S=\mathbb {P}^1$
and
![]() $q_{*}F_W|_F\neq 0$
, then
$q_{*}F_W|_F\neq 0$
, then
![]() $q_{*}F_W|_F$
is a movable effective nonzero integral divisor on F. Restricting (4.3) on F, we have
$q_{*}F_W|_F$
is a movable effective nonzero integral divisor on F. Restricting (4.3) on F, we have
![]() $ -K_F\sim _{{\mathbb {Q}}}\omega (q_{*}F_W|_F)+E_Y|_F. $
By Lemma 4.4,
$ -K_F\sim _{{\mathbb {Q}}}\omega (q_{*}F_W|_F)+E_Y|_F. $
By Lemma 4.4,
![]() $\omega \leq 4$
.
$\omega \leq 4$
.
Case 3. S is a del Pezzo surface.
In this case,
![]() $\omega \leq 12$
by (4.3) and Lemma 4.7.
$\omega \leq 12$
by (4.3) and Lemma 4.7.
Combining all above cases, we proved that
![]() $\frac {P_{-m}-1}{m}=\omega \leq 12$
as long as
$\frac {P_{-m}-1}{m}=\omega \leq 12$
as long as
![]() $|-mK_X|$
is composed with a pencil.
$|-mK_X|$
is composed with a pencil.
Applying Proposition 4.1 and Theorem 4.2, we have the following criteria for
![]() $|-mK|$
not composed with a pencil (cf. [Reference Chen and Jiang6, Prop. 5.4]).
$|-mK|$
not composed with a pencil (cf. [Reference Chen and Jiang6, Prop. 5.4]).
Proposition 4.8. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Let t be a positive real number, and let m be a positive integer. If
${\mathbb {Q}}$
-Fano threefold. Let t be a positive real number, and let m be a positive integer. If
![]() $m\geq t, m\geq \frac {r_{\max }t}{3}$
, and one of the following conditions holds:
$m\geq t, m\geq \frac {r_{\max }t}{3}$
, and one of the following conditions holds:
-
(1)
 $m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+6r_X+\frac {1}{16}}$
,
$m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+6r_X+\frac {1}{16}}$
, -
(2)
 $m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+\frac {72}{-K_{X}^3}+\frac {1}{16}}$
,
$m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+\frac {72}{-K_{X}^3}+\frac {1}{16}}$
,
then
![]() $|-m K_{X}|$
is not composed with a pencil.
$|-m K_{X}|$
is not composed with a pencil.
Proof. By [Reference Chen and Jiang6, Prop. 5.3],
The assumption implies that either
![]() $P_{-m}>r_X(-K_X^3) m+1$
or
$P_{-m}>r_X(-K_X^3) m+1$
or
![]() $P_{-m}>12m+1$
. Hence,
$P_{-m}>12m+1$
. Hence,
![]() $|-m K_{X}|$
is not composed with a pencil by Proposition 4.1 and Theorem 4.2.
$|-m K_{X}|$
is not composed with a pencil by Proposition 4.1 and Theorem 4.2.
By the same method, we have the following corollary.
Corollary 4.9. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. Let t be a positive real number, and let m be a positive integer. If
${\mathbb {Q}}$
-Fano threefold. Let t be a positive real number, and let m be a positive integer. If
![]() $m\geq t, m\geq \frac {r_{\max }t}{3}$
, and
$m\geq t, m\geq \frac {r_{\max }t}{3}$
, and
![]() $m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+\frac {6}{l\cdot (-K_{X}^3)}+\frac {1}{16}}$
for some positive real number l, then
$m>-\frac {3}{4}+\sqrt {\frac {12}{t\cdot (-K_{X}^3)}+\frac {6}{l\cdot (-K_{X}^3)}+\frac {1}{16}}$
for some positive real number l, then
![]() $P_{-m}-1>\frac {m}{l}$
.
$P_{-m}-1>\frac {m}{l}$
.
We illustrate in the following example on how efficient Proposition 4.8 is comparing to [Reference Chen and Jiang5, Cor. 4.2].
Example 4.10. Suppose that X is a terminal weak
![]() $\mathbb {Q}$
-Fano threefold with
$\mathbb {Q}$
-Fano threefold with
![]() $P_{-1}=0$
,
$P_{-1}=0$
,
![]() $B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
, and
$B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
, and
![]() $-K_X^3=\frac {43}{315}$
. Then [Reference Chen and Jiang5, Cor. 4.2] implies that
$-K_X^3=\frac {43}{315}$
. Then [Reference Chen and Jiang5, Cor. 4.2] implies that
![]() $|-mK_X|$
is not composed with a pencil for all
$|-mK_X|$
is not composed with a pencil for all
![]() $m\geq 61$
(see the last paragraph of [Reference Chen and Jiang5, p. 106]). On the other hand, by Proposition 4.8,
$m\geq 61$
(see the last paragraph of [Reference Chen and Jiang5, p. 106]). On the other hand, by Proposition 4.8,
![]() $|-mK_X|$
is not composed with a pencil for all
$|-mK_X|$
is not composed with a pencil for all
![]() $m\geq 23$
(see Case 4 of Proof of Theorem 5.6), which significantly improves the previous result. Also, it can be computed directly by (2.1) to get
$m\geq 23$
(see Case 4 of Proof of Theorem 5.6), which significantly improves the previous result. Also, it can be computed directly by (2.1) to get
![]() $P_{-22}=260<12\times 22+1$
, which tells that the estimates in Proposition 4.8 are efficient enough comparing to directly using the Riemann–Roch formula.
$P_{-22}=260<12\times 22+1$
, which tells that the estimates in Proposition 4.8 are efficient enough comparing to directly using the Riemann–Roch formula.
4.4 A remark on [Reference Chen and Jiang5, Cor. 4.2]
In this subsection, we discuss the equality case of [Reference Chen and Jiang5, Cor. 4.2] for terminal
![]() ${\mathbb {Q}}$
-Fano threefolds.
${\mathbb {Q}}$
-Fano threefolds.
Proposition 4.11. Let X be a terminal
![]() ${\mathbb {Q}}$
-Fano threefold, and let m be a positive integer. If
${\mathbb {Q}}$
-Fano threefold, and let m be a positive integer. If
and
![]() $|-m K_X|$
is composed with a pencil, then:
$|-m K_X|$
is composed with a pencil, then:
-
(1)
 $r_X(-K_X^3)=1$
.
$r_X(-K_X^3)=1$
. -
(2) If, moreover, the Weil divisor class group of X has no m-torsion element, then
 $h^0(X, -kK_X)$
$h^0(X, -kK_X)$
 $=k+1$
for all
$=k+1$
for all
 $1\leq k\leq m$
.
$1\leq k\leq m$
.
Proof. We recall the proof of [Reference Chen and Jiang5, Cor. 4.2]. As
![]() $|-m K_X|$
is composed with a pencil, take
$|-m K_X|$
is composed with a pencil, take
![]() $D=-mK_X$
and keep the notation in §2.1, we have
$D=-mK_X$
and keep the notation in §2.1, we have
where S is a generic irreducible element of
![]() $\operatorname {Mov}|\lfloor \pi ^*(-mK_X) \rfloor |$
and F is an effective
$\operatorname {Mov}|\lfloor \pi ^*(-mK_X) \rfloor |$
and F is an effective
![]() $\mathbb {Q}$
-divisor. Then
$\mathbb {Q}$
-divisor. Then
by [Reference Chen and Jiang5, Lem. 4.1].
Now, by assumption, the equality holds. So
![]() $(\pi ^*(-K_X)^2\cdot F)=0$
. This implies that F is
$(\pi ^*(-K_X)^2\cdot F)=0$
. This implies that F is
![]() $\pi $
-exceptional as
$\pi $
-exceptional as
![]() $-K_X$
is ample. So (4.4) implies that
$-K_X$
is ample. So (4.4) implies that
Then
By [Reference Jiang9, Lem. 2.3],
![]() $(\pi _*S)^3\geq \frac {1}{r_X}$
. Then (4.5) implies that
$(\pi _*S)^3\geq \frac {1}{r_X}$
. Then (4.5) implies that
 $$ \begin{align*}-K_X^3\geq \frac{(r_X(-K_X^3))^3}{r_X}, \end{align*} $$
$$ \begin{align*}-K_X^3\geq \frac{(r_X(-K_X^3))^3}{r_X}, \end{align*} $$
which implies that
![]() $r_X(-K_X^3)=1$
as it is a positive integer. Under the assumption that the Weil divisor class group of X has no m-torsion element, (4.5) implies that
$r_X(-K_X^3)=1$
as it is a positive integer. Under the assumption that the Weil divisor class group of X has no m-torsion element, (4.5) implies that
![]() $-K_X\sim \pi _*S$
. So the conclusion follows as
$-K_X\sim \pi _*S$
. So the conclusion follows as
![]() $-kK_X\sim k\pi _*S$
is composed with a pencil for any
$-kK_X\sim k\pi _*S$
is composed with a pencil for any
![]() $1\leq k\leq m$
(see [Reference Chen and Jiang5, p. 63, Case (
$1\leq k\leq m$
(see [Reference Chen and Jiang5, p. 63, Case (
![]() ${f}_p$
)]).
${f}_p$
)]).
The following example shows that Proposition 4.11 is nonempty.
Example 4.12 [Reference Iano-Fletcher8, List 16.6, No. 88]
A general weighted hypersurface
![]() $X_{42}\subset \mathbb {P}(1, 1$
,
$X_{42}\subset \mathbb {P}(1, 1$
,
![]() $6, 14, 21)$
is a terminal
$6, 14, 21)$
is a terminal
![]() $\mathbb {Q}$
-Fano threefold with
$\mathbb {Q}$
-Fano threefold with
![]() $r_X(-K_X^3)=1$
and
$r_X(-K_X^3)=1$
and
![]() $B_X=\{(1, 2), (1, 3), (1, 7)\}$
. By [Reference Prokhorov18, Prop. 2.9], the Weil divisor class group of X is torsion-free. Certainly,
$B_X=\{(1, 2), (1, 3), (1, 7)\}$
. By [Reference Prokhorov18, Prop. 2.9], the Weil divisor class group of X is torsion-free. Certainly,
![]() $P_{-k}=k+1$
and
$P_{-k}=k+1$
and
![]() $|-kK_X|$
is composed with a pencil for
$|-kK_X|$
is composed with a pencil for
![]() $1\leq k\leq 5$
.
$1\leq k\leq 5$
.
5 Proofs of main results
In this section, we apply the birationality criteria (Theorem 3.4 and Corollary 3.7) and the non-pencil criteria (Proposition 4.8) to prove the main theorem. The proof will be divided into several cases:
-
1.
 $r_X=840$
.
$r_X=840$
. -
2.
 $P_{-2}=0$
.
$P_{-2}=0$
. -
3.
 $P_{-2}>0$
,
$P_{-2}>0$
,
 $P_{-1}=0$
, and
$P_{-1}=0$
, and
 $r_{\max }\geq 14$
.
$r_{\max }\geq 14$
. -
4.
 $P_{-2}>0$
,
$P_{-2}>0$
,
 $P_{-1}=0$
, and
$P_{-1}=0$
, and
 $r_{\max }\leq 13$
.
$r_{\max }\leq 13$
. -
5.
 $P_{-1}>0$
and
$P_{-1}>0$
and
 $r_{\max }\geq 14$
.
$r_{\max }\geq 14$
. -
6.
 $P_{-1}>0$
and
$P_{-1}>0$
and
 $r_{\max }\leq 13$
.
$r_{\max }\leq 13$
.
Here, recall that
![]() $r_X={\text {lcm}}\{r_i\mid r_i\in \mathcal {R}_X\}$
is the Cartier index of
$r_X={\text {lcm}}\{r_i\mid r_i\in \mathcal {R}_X\}$
is the Cartier index of
![]() $K_X$
, and
$K_X$
, and
![]() $r_{\max }=\max \{r_i\mid r_i\in \mathcal {R}_X\}$
is the maximal local index.
$r_{\max }=\max \{r_i\mid r_i\in \mathcal {R}_X\}$
is the maximal local index.
5.1 The case
 $r_{X}=840$
$r_{X}=840$
Theorem 5.1. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold with
${\mathbb {Q}}$
-Fano threefold with
![]() $r_{X}=840$
. Then
$r_{X}=840$
. Then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
Proof. Keep the setting in Notation 3.1. By [Reference Chen and Jiang6, Lem. 6.5] and the first line of its proof, we know that
![]() $r_{\max }=8$
,
$r_{\max }=8$
,
![]() $P_{-1}\geq 1$
, and
$P_{-1}\geq 1$
, and
![]() $-K_X^3\geq \frac {47}{840}$
. Take
$-K_X^3\geq \frac {47}{840}$
. Take
![]() $m_0=8$
and
$m_0=8$
and
![]() $\nu _0=1$
. By Corollary 4.9 (with
$\nu _0=1$
. By Corollary 4.9 (with
![]() $l=1$
,
$l=1$
,
![]() $t=4.5$
, and
$t=4.5$
, and
![]() $-K_X^3\geq \frac {47}{840}$
), we have
$-K_X^3\geq \frac {47}{840}$
), we have
![]() $P_{-12}-1>12.$
$P_{-12}-1>12.$
If
![]() $|-12K_X|$
and
$|-12K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {12}{P_{-12}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
$\mu _0'=\frac {12}{P_{-12}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
![]() $t=13.5$
and
$t=13.5$
and
![]() $-K_X^3\geq \frac {47}{840}$
), we can take
$-K_X^3\geq \frac {47}{840}$
), we can take
![]() $m_1=36$
. By Lemma 3.3,
$m_1=36$
. By Lemma 3.3,
![]() $N_0\geq \lceil {\frac {840}{8m_1}}\rceil = 3.$
Then, by Corollary 3.7(1),
$N_0\geq \lceil {\frac {840}{8m_1}}\rceil = 3.$
Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
If
![]() $|-12K_X|$
and
$|-12K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=12$
and
$m_1=12$
and
![]() $\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
$\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 36$
.
$m\geq 36$
.
5.2 The case
 $P_{-2}=0$
$P_{-2}=0$
Theorem 5.2. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-2}=0$
, then
$P_{-2}=0$
, then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 51$
.
$m\geq 51$
.
Proof. Keep the setting in Notation 3.1. In this case, the possible baskets are classified in [Reference Chen and Chen2, Th. 3.5] with 23 cases in total (see Table A.1 in the Appendix). Here, we refer to the numbering in Table A.1.
For Nos. 1–5 of Table A.1,
![]() $r_{X} \leq 84, -K_{X}^{3} \geq \frac {1}{84}$
,
$r_{X} \leq 84, -K_{X}^{3} \geq \frac {1}{84}$
,
![]() $P_{-8}\geq 2$
, and
$P_{-8}\geq 2$
, and
![]() $r_{\max } \leq 11$
. So we can take
$r_{\max } \leq 11$
. So we can take
![]() $m_0=8$
. By Corollary 4.9 (with
$m_0=8$
. By Corollary 4.9 (with
![]() $l=2$
and
$l=2$
and
![]() $t=5.7$
),
$t=5.7$
),
![]() $P_{-21}-1>\frac {21}{2}$
. If
$P_{-21}-1>\frac {21}{2}$
. If
![]() $|-21K_X|$
and
$|-21K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {21}{P_{-21}-1}<2$
by Remark 3.2. By Proposition 4.8(1) (with
$\mu _0'=\frac {21}{P_{-21}-1}<2$
by Remark 3.2. By Proposition 4.8(1) (with
![]() $t=6.6$
), we can take
$t=6.6$
), we can take
![]() $m_{1}=25$
. Then, by Theorem 3.4(2),
$m_{1}=25$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 48$
. If
$m \geq 48$
. If
![]() $|-21K_X|$
and
$|-21K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=21$
and
$m_1=21$
and
![]() $\mu _{0}'=m_0=8$
. Then, by Theorem 3.4(2),
$\mu _{0}'=m_0=8$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 51$
.
$m \geq 51$
.
For Nos. 6–13 and Nos. 16–23 of Table A.1,
![]() $r_{X} \leq 78, -K_{X}^{3} \geq \frac {1}{30}$
,
$r_{X} \leq 78, -K_{X}^{3} \geq \frac {1}{30}$
,
![]() $P_{-6}\geq 2$
, and
$P_{-6}\geq 2$
, and
![]() $r_{\max } \leq 14$
. So we can take
$r_{\max } \leq 14$
. So we can take
![]() $m_0=6$
. By Corollary 4.9 (with
$m_0=6$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=3.6$
),
$t=3.6$
),
![]() $P_{-17}-1>17$
. If
$P_{-17}-1>17$
. If
![]() $|-17K_X|$
and
$|-17K_X|$
and
![]() $|-6K_X|$
are composed with the same pencil, then take
$|-6K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {17}{P_{-17}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
$\mu _0'=\frac {17}{P_{-17}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
![]() $t=4.9$
), we can take
$t=4.9$
), we can take
![]() $m_{1}=23$
. Then, by Theorem 3.4(2),
$m_{1}=23$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 51$
. If
$m \geq 51$
. If
![]() $|-17K_X|$
and
$|-17K_X|$
and
![]() $|-6K_X|$
are not composed with the same pencil, then take
$|-6K_X|$
are not composed with the same pencil, then take
![]() $m_1=17$
and
$m_1=17$
and
![]() $\mu _{0}'=m_0=6$
. Then, by Theorem 3.4(2),
$\mu _{0}'=m_0=6$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 51$
.
$m \geq 51$
.
For No. 14 of Table A.1,
![]() $r_{X}=210, -K_{X}^{3}=\frac {17}{210}$
,
$r_{X}=210, -K_{X}^{3}=\frac {17}{210}$
,
![]() $P_{-5}=2$
, and
$P_{-5}=2$
, and
![]() $r_{\max }=7$
. So we can take
$r_{\max }=7$
. So we can take
![]() $m_0=5$
. By Corollary 4.9 (with
$m_0=5$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=4.2$
),
$t=4.2$
),
![]() $P_{-10}-1>10$
. If
$P_{-10}-1>10$
. If
![]() $|-10K_X|$
and
$|-10K_X|$
and
![]() $|-5K_X|$
are composed with the same pencil, then take
$|-5K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {10}{P_{-10}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
$\mu _0'=\frac {10}{P_{-10}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
![]() $t=12$
), we can take
$t=12$
), we can take
![]() $m_{1}=30$
. Then, by Theorem 3.4(2),
$m_{1}=30$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 51$
. If
$m \geq 51$
. If
![]() $|-10K_X|$
and
$|-10K_X|$
and
![]() $|-5K_X|$
are not composed with the same pencil, then take
$|-5K_X|$
are not composed with the same pencil, then take
![]() $m_1=10$
and
$m_1=10$
and
![]() $\mu _{0}'=m_0=5$
. Then, by Theorem 3.4(2),
$\mu _{0}'=m_0=5$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 29$
.
$m \geq 29$
.
For No. 15 of Table A.1,
![]() $r_{X}=120, -K_{X}^{3}=\frac {3}{40}$
,
$r_{X}=120, -K_{X}^{3}=\frac {3}{40}$
,
![]() $P_{-5}=2$
, and
$P_{-5}=2$
, and
![]() $r_{\max }=8$
. So we can take
$r_{\max }=8$
. So we can take
![]() $m_0=5$
. By Corollary 4.9 (with
$m_0=5$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=4$
),
$t=4$
),
![]() $P_{-11}-1>11$
. If
$P_{-11}-1>11$
. If
![]() $|-11K_X|$
and
$|-11K_X|$
and
![]() $|-5K_X|$
are composed with the same pencil, then take
$|-5K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {11}{P_{-11}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
$\mu _0'=\frac {11}{P_{-11}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
![]() $t=10$
), we can take
$t=10$
), we can take
![]() $m_{1}=27$
. Then, by Theorem 3.4(2),
$m_{1}=27$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 46$
. If
$m \geq 46$
. If
![]() $|-11K_X|$
and
$|-11K_X|$
and
![]() $|-5K_X|$
are not composed with the same pencil, then take
$|-5K_X|$
are not composed with the same pencil, then take
![]() $m_1=11$
and
$m_1=11$
and
![]() $\mu _{0}'=m_0=5$
. Then, by Theorem 3.4(2),
$\mu _{0}'=m_0=5$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 32$
.
$m \geq 32$
.
5.3 The case
 $P_{-2}>0$
and
$P_{-2}>0$
and
 $P_{-1}=0$
$P_{-1}=0$
Lemma 5.3. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-1}=0$
and
$P_{-1}=0$
and
![]() $P_{-2}>0$
, then
$P_{-2}>0$
, then
Proof. By (2.3), we have
![]() $\sigma (B_X)=10-5P_{-1}+P_{-2}=10+P_{-2}\geq 11$
. Other statements follow from (2.4) and Proposition 2.2(4).
$\sigma (B_X)=10-5P_{-1}+P_{-2}=10+P_{-2}\geq 11$
. Other statements follow from (2.4) and Proposition 2.2(4).
Theorem 5.4. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-2}>0$
,
$P_{-2}>0$
,
![]() $P_{-1}=0$
, and
$P_{-1}=0$
, and
![]() $r_{\max }\geq 14$
, then
$r_{\max }\geq 14$
, then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 59$
. Moreover,
$m\geq 59$
. Moreover,
![]() $\varphi _{-58}$
may not be birational only if
$\varphi _{-58}$
may not be birational only if
![]() $B_X=\{(1, 2), 2\times (1, 3), (8, 17)\}$
and
$B_X=\{(1, 2), 2\times (1, 3), (8, 17)\}$
and
![]() $|-24K_X|$
is composed with a pencil.
$|-24K_X|$
is composed with a pencil.
Proof. Keep the setting in Notation 3.1. By [Reference Chen and Jiang5, Case II of Proof of Th. 3.12] (especially the last paragraph of Subsubcase II-3-iii) or the second paragraph of [Reference Chen and Jiang5, Case IV of Proof of Th. 1.8] (see Table A.2 in the Appendix), we can see that
![]() $r_{\max }\leq 13$
provided
$r_{\max }\leq 13$
provided
![]() $P_{-4}=1$
. Hence, by assumption,
$P_{-4}=1$
. Hence, by assumption,
![]() $P_{-4}\geq 2$
, and we can always take
$P_{-4}\geq 2$
, and we can always take
![]() $m_0=4$
.
$m_0=4$
.
Case 1.
![]() $ r_{\max }\geq 16$
.
$ r_{\max }\geq 16$
.
It is not hard to search by hands or with the help of a computer program to get all possible
![]() $B_X$
satisfying (5.1) and
$B_X$
satisfying (5.1) and
![]() $r_{\max }\geq 16$
. Here, note that
$r_{\max }\geq 16$
. Here, note that
![]() $\sigma (B_X) \geq 11$
implies that
$\sigma (B_X) \geq 11$
implies that
![]() $\sum _i r_i> 2\sigma (B_X)\geq 22.$
$\sum _i r_i> 2\sigma (B_X)\geq 22.$
If
![]() $22\leq r_{\max }\leq 24$
, then there is no
$22\leq r_{\max }\leq 24$
, then there is no
![]() $B_X$
satisfying (5.1). If
$B_X$
satisfying (5.1). If
![]() $16\leq r_{\max }\leq 21$
, then all possible
$16\leq r_{\max }\leq 21$
, then all possible
![]() $B_X$
satisfying (5.1) are listed in Table 1.
$B_X$
satisfying (5.1) are listed in Table 1.
Table 1 Baskets satisfying Lemma 5.3 with
![]() $r_{\max }\geq 16$
.
$r_{\max }\geq 16$
.

Here, we explain briefly how to get Table 1. The algorithm is the following: first, we can list all possible
![]() $\mathcal {R}_X$
satisfying
$\mathcal {R}_X$
satisfying
![]() $2\in \mathcal {R}_X$
and
$2\in \mathcal {R}_X$
and
![]() $\gamma (B_X)\geq 0$
; then we find all possible
$\gamma (B_X)\geq 0$
; then we find all possible
![]() $b_i$
for those
$b_i$
for those
![]() $\mathcal {R}_X$
such that
$\mathcal {R}_X$
such that
![]() $\sigma (B_X)\geq 11$
. For example, let us consider the case
$\sigma (B_X)\geq 11$
. For example, let us consider the case
![]() $r_{\max }=17$
. As
$r_{\max }=17$
. As
![]() $2\in \mathcal {R}_X$
,
$2\in \mathcal {R}_X$
,
![]() $\{2, 17\}\subset \mathcal {R}_X$
. So we can list all possible
$\{2, 17\}\subset \mathcal {R}_X$
. So we can list all possible
![]() $\mathcal {R}_X$
with
$\mathcal {R}_X$
with
![]() $\gamma (B_X)\geq 0$
by enumeration method by considering the second largest
$\gamma (B_X)\geq 0$
by enumeration method by considering the second largest
![]() $r_i$
:
$r_i$
:

Then all possible
![]() $B_X$
with
$B_X$
with
![]() $\sigma (B_X)\geq 11$
are listed in Table 1; for instance, there is no such basket
$\sigma (B_X)\geq 11$
are listed in Table 1; for instance, there is no such basket
![]() $B_X$
with
$B_X$
with
![]() $\mathcal {R}_X=\{2,4, 17\}$
because in this case
$\mathcal {R}_X=\{2,4, 17\}$
because in this case
![]() $\sigma (B_X)\leq 1+1+8=10.$
$\sigma (B_X)\leq 1+1+8=10.$
For No. 2 of Table 1,
![]() $-K_X^3=\frac {5}{21}$
, and in this case,
$-K_X^3=\frac {5}{21}$
, and in this case,
![]() $P_{-2}=2$
,
$P_{-2}=2$
,
![]() $r_X=42$
, and
$r_X=42$
, and
![]() $r_{\max }=21$
. We can take
$r_{\max }=21$
. We can take
![]() $\mu _{0}'=m_0=2$
. By Proposition 4.8(1) (with
$\mu _{0}'=m_0=2$
. By Proposition 4.8(1) (with
![]() $t=2.28$
), we can take
$t=2.28$
), we can take
![]() $m_1=16$
. Then, by Theorem 3.4(1),
$m_1=16$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 54$
.
$m \geq 54$
.
For other cases with
![]() $-K_X^3>0$
, we have
$-K_X^3>0$
, we have
![]() $-K_X^3\geq \frac {7}{102}$
and
$-K_X^3\geq \frac {7}{102}$
and
![]() $r_{\max }\leq 19$
. By Corollary 4.9 (with
$r_{\max }\leq 19$
. By Corollary 4.9 (with
![]() $l=1$
,
$l=1$
,
![]() $t=2$
),
$t=2$
),
![]() $P_{-13}-1>13$
. If
$P_{-13}-1>13$
. If
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-4K_X|$
are not composed with the same pencil, then take
$|-4K_X|$
are not composed with the same pencil, then take
![]() $m_1=13$
and
$m_1=13$
and
![]() $\mu _{0}'=m_0=4$
. Then, by Theorem 3.4(1),
$\mu _{0}'=m_0=4$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 51$
.
$m\geq 51$
.
So we may assume that
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-4K_X|$
are composed with the same pencil. Then, in the following, we can take
$|-4K_X|$
are composed with the same pencil. Then, in the following, we can take
![]() $\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2 and
$\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2 and
![]() $m_0=4$
.
$m_0=4$
.
For Nos. 6–8 of Table 1,
![]() $-K_X^3\geq \frac {5}{38}$
,
$-K_X^3\geq \frac {5}{38}$
,
![]() $r_X\leq 38$
, and
$r_X\leq 38$
, and
![]() $r_{\max }\leq 19$
. By Proposition 4.8(1) (with
$r_{\max }\leq 19$
. By Proposition 4.8(1) (with
![]() $t=2.4$
), we can take
$t=2.4$
), we can take
![]() $m_1=16$
. Then, by Theorem 3.4(1),
$m_1=16$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 50$
.
$m \geq 50$
.
For Nos. 14–16 and Nos. 18 and 19 of Table 1,
![]() $-K_X^3\geq \frac {5}{48}$
,
$-K_X^3\geq \frac {5}{48}$
,
![]() $r_X\leq 80$
, and
$r_X\leq 80$
, and
![]() $r_{\max }\leq 17$
. By Proposition 4.8(1) (with
$r_{\max }\leq 17$
. By Proposition 4.8(1) (with
![]() $t=3.88$
), we can take
$t=3.88$
), we can take
![]() $m_1=22$
. Then, by Theorem 3.4(2),
$m_1=22$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 56$
.
$m \geq 56$
.
For No. 13 of Table 1,
![]() $-K_X^3=\frac {7}{102}$
,
$-K_X^3=\frac {7}{102}$
,
![]() $r_X=102$
, and
$r_X=102$
, and
![]() $r_{\max }=17$
. By Proposition 4.8(1) (with
$r_{\max }=17$
. By Proposition 4.8(1) (with
![]() $t=3.6$
), we can take
$t=3.6$
), we can take
![]() $m_1=25$
. Then, by Theorem 3.4(2),
$m_1=25$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 59$
. Moreover, if
$m \geq 59$
. Moreover, if
![]() $|-24K_X|$
is not composed with a pencil, then take
$|-24K_X|$
is not composed with a pencil, then take
![]() $m_1=24$
. Then, by Theorem 3.4(2),
$m_1=24$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m \geq 58$
.
$m \geq 58$
.
Case 2.
![]() $ 14\leq r_{\max }\leq 15$
.
$ 14\leq r_{\max }\leq 15$
.
For the remaining cases
![]() $14\leq r_{\max }\leq 15$
, we have
$14\leq r_{\max }\leq 15$
, we have
![]() $-K_X^3\geq \frac {1}{30}$
by Proposition 2.2(3) as
$-K_X^3\geq \frac {1}{30}$
by Proposition 2.2(3) as
![]() $P_{-4}\geq 2$
. By Corollary 4.9 (with
$P_{-4}\geq 2$
. By Corollary 4.9 (with
![]() $l=1, t=3.4$
),
$l=1, t=3.4$
),
![]() $P_{-17}-1>17$
.
$P_{-17}-1>17$
.
If
![]() $|-17K_X|$
and
$|-17K_X|$
and
![]() $|-4K_X|$
are not composed with the same pencil, then take
$|-4K_X|$
are not composed with the same pencil, then take
![]() $m_1=17$
and
$m_1=17$
and
![]() $\mu _0'=m_0=4$
. Then, by Theorem 3.4(2),
$\mu _0'=m_0=4$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 51$
.
$m\geq 51$
.
If
![]() $|-17K_X|$
and
$|-17K_X|$
and
![]() $|-4K_X|$
are composed with the same pencil, then take
$|-4K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {17}{P_{-17}-1}<1$
by Remark 3.2 and
$\mu _0'=\frac {17}{P_{-17}-1}<1$
by Remark 3.2 and
![]() $m_0=4$
.
$m_0=4$
.
If
![]() $r_{\max }=15$
, then we claim that
$r_{\max }=15$
, then we claim that
![]() $r_X\leq 60$
. In fact, as
$r_X\leq 60$
. In fact, as
![]() $\{15, 2\}\subset \mathcal {R}_X$
, by (2.4),
$\{15, 2\}\subset \mathcal {R}_X$
, by (2.4),
![]() $s\not \in \mathcal {R}_X$
for all
$s\not \in \mathcal {R}_X$
for all
![]() $s>7$
. If
$s>7$
. If
![]() $7\not \in \mathcal {R}_X$
, then
$7\not \in \mathcal {R}_X$
, then
![]() $r_X$
divides
$r_X$
divides
![]() $60$
. If
$60$
. If
![]() $7\in \mathcal {R}_X$
, then
$7\in \mathcal {R}_X$
, then
![]() $\mathcal {R}_X=\{15, 7, 2\}$
by (2.4), and moreover
$\mathcal {R}_X=\{15, 7, 2\}$
by (2.4), and moreover
![]() $B_X=\{(1, 2), (3, 7), (7, 15)\}$
by
$B_X=\{(1, 2), (3, 7), (7, 15)\}$
by
![]() $\sigma (B_X)\geq 11$
. But this basket has
$\sigma (B_X)\geq 11$
. But this basket has
![]() $-K_X^3<0$
by (2.2), which is absurd. Hence,
$-K_X^3<0$
by (2.2), which is absurd. Hence,
![]() $r_X\leq 60$
. By Proposition 4.8(1) (with
$r_X\leq 60$
. By Proposition 4.8(1) (with
![]() $t=4$
,
$t=4$
,
![]() $-K_X^3\geq \frac {1}{30}$
), we can take
$-K_X^3\geq \frac {1}{30}$
), we can take
![]() $m_1=21$
. Then, by Theorem 3.4(2),
$m_1=21$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 51$
.
$m\geq 51$
.
If
![]() $r_{\max }=14$
, then we claim that
$r_{\max }=14$
, then we claim that
![]() $B_X=\{6\times (1, 2), (5, 14)\}$
. Suppose that
$B_X=\{6\times (1, 2), (5, 14)\}$
. Suppose that
![]() $B_X=\{(b_1, r_1), \dots , (b_k, r_k), (b, 14)\}$
with
$B_X=\{(b_1, r_1), \dots , (b_k, r_k), (b, 14)\}$
with
![]() $b\in \{1,3,5\}$
. Then
$b\in \{1,3,5\}$
. Then
![]() $\sigma (B_X)\geq 11$
implies that
$\sigma (B_X)\geq 11$
implies that
![]() $\sum _{i=1}^kb_i\geq 6$
. If there exists some
$\sum _{i=1}^kb_i\geq 6$
. If there exists some
![]() $r_i>2$
, then
$r_i>2$
, then
![]() $\sum _{i=1}^kr_i>2\sum _{i=1}^kb_i\geq 12$
, that is,
$\sum _{i=1}^kr_i>2\sum _{i=1}^kb_i\geq 12$
, that is,
![]() $\sum _{i=1}^kr_i\geq 13$
. So (2.4) implies that
$\sum _{i=1}^kr_i\geq 13$
. So (2.4) implies that
![]() $\sum _{i=1}^k\frac {1}{r_i}\geq 3-\frac {1}{14}$
. On the other hand, (2.4) implies that
$\sum _{i=1}^k\frac {1}{r_i}\geq 3-\frac {1}{14}$
. On the other hand, (2.4) implies that
![]() $\frac {3}{2}k+14-\frac {1}{14}\leq 24$
, which says that
$\frac {3}{2}k+14-\frac {1}{14}\leq 24$
, which says that
![]() $k\leq 6.$
So
$k\leq 6.$
So
![]() $\sum _{i=1}^k\frac {1}{r_i}\leq 5\times \frac {1}{2}+\frac {1}{3}<3-\frac {1}{14}$
, a contradiction. So all
$\sum _{i=1}^k\frac {1}{r_i}\leq 5\times \frac {1}{2}+\frac {1}{3}<3-\frac {1}{14}$
, a contradiction. So all
![]() $r_i= 2$
and
$r_i= 2$
and
![]() $k\geq 6$
. Then
$k\geq 6$
. Then
![]() $\gamma (B_X)\geq 0$
implies that
$\gamma (B_X)\geq 0$
implies that
![]() $k=6$
, and
$k=6$
, and
![]() $\sigma (B_X)\geq 11$
implies that
$\sigma (B_X)\geq 11$
implies that
![]() $b=5$
. We conclude that
$b=5$
. We conclude that
![]() $B_X=\{6\times (1, 2), (5, 14)\}$
. In this case,
$B_X=\{6\times (1, 2), (5, 14)\}$
. In this case,
![]() $-K_X^3=\frac {3}{14}$
and
$-K_X^3=\frac {3}{14}$
and
![]() $r_X=r_{\max }=14$
. By Proposition 4.8(1) (with
$r_X=r_{\max }=14$
. By Proposition 4.8(1) (with
![]() $t=2$
), we can take
$t=2$
), we can take
![]() $m_1=10$
. Then, by Theorem 3.4(1),
$m_1=10$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 32$
.
$m\geq 32$
.
Combining all above cases, we have proved the theorem.
Lemma 5.5. (cf. [Reference Chen and Chen2, Case I of Proof of Th. 4.4])
Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold with
${\mathbb {Q}}$
-Fano threefold with
![]() $P_{-1}=0$
and
$P_{-1}=0$
and
![]() $P_{-2}>0$
. If
$P_{-2}>0$
. If
![]() $P_{-4}\geq 2$
and
$P_{-4}\geq 2$
and
![]() $-K_X^3<\frac {1}{12}$
, then
$-K_X^3<\frac {1}{12}$
, then
![]() $B_X$
is dominated by one of the following initial baskets:
$B_X$
is dominated by one of the following initial baskets:
 $$ \begin{align*} {}&\{8\times(1, 2), 3\times(1, 3)\},\\ {}&\{9\times(1, 2), (1, 4), (1, 5)\},\\ {}&\{9\times(1, 2), (1, 4), (1, 6)\},\\ {}&\{9\times(1, 2), 2\times (1, 5)\}. \end{align*} $$
$$ \begin{align*} {}&\{8\times(1, 2), 3\times(1, 3)\},\\ {}&\{9\times(1, 2), (1, 4), (1, 5)\},\\ {}&\{9\times(1, 2), (1, 4), (1, 6)\},\\ {}&\{9\times(1, 2), 2\times (1, 5)\}. \end{align*} $$
Note that in the latter three cases, all possible packings have
![]() $r_{\max }\leq 9$
.
$r_{\max }\leq 9$
.
Proof. Following [Reference Chen and Chen2, Case I of Proof of Th. 4.4], we only need to consider the cases
![]() $(P_{-3}, P_{-4})=(1, 2)$
or
$(P_{-3}, P_{-4})=(1, 2)$
or
![]() $(0, 2)$
in [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4].
$(0, 2)$
in [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4].
If
![]() $(P_{-3}, P_{-4})=(1, 2)$
, then [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4] shows that
$(P_{-3}, P_{-4})=(1, 2)$
, then [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4] shows that
![]() $B_X$
is dominated by
$B_X$
is dominated by
![]() $\{8\times (1, 2), 3\times (1, 3)\}$
. (Actually, it shows moreover that
$\{8\times (1, 2), 3\times (1, 3)\}$
. (Actually, it shows moreover that
![]() $B_X$
is dominated by
$B_X$
is dominated by
![]() $\{7\times (1, 2), (2, 5), 2\times (1, 3)\}$
.)
$\{7\times (1, 2), (2, 5), 2\times (1, 3)\}$
.)
If
![]() $(P_{-3}, P_{-4})=(0, 2)$
, then
$(P_{-3}, P_{-4})=(0, 2)$
, then
![]() $P_{-1}=0$
and
$P_{-1}=0$
and
![]() $P_{-2}=1$
. Then, by (2.5)–(2.7),
$P_{-2}=1$
. Then, by (2.5)–(2.7),
![]() $n^0_{1, 2}=9$
,
$n^0_{1, 2}=9$
,
![]() $n^0_{1, 3}=0$
, and
$n^0_{1, 3}=0$
, and
![]() $n^0_{1, 4}+\sigma _5=2$
. So
$n^0_{1, 4}+\sigma _5=2$
. So
![]() $B_X$
is dominated by
$B_X$
is dominated by
![]() $\{9\times (1, 2), (1, s_1), (1, s_2)\}$
for some
$\{9\times (1, 2), (1, s_1), (1, s_2)\}$
for some
![]() $s_2\geq s_1\geq 4$
. The case
$s_2\geq s_1\geq 4$
. The case
![]() $(s_1, s_2)=(4, 4)$
is ruled out by [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4]. Hence, we get the conclusion by (2.4) and [Reference Chen and Chen2, Lem. 3.1].
$(s_1, s_2)=(4, 4)$
is ruled out by [Reference Chen and Chen2, Subcase I-3 of Proof of Th. 4.4]. Hence, we get the conclusion by (2.4) and [Reference Chen and Chen2, Lem. 3.1].
Theorem 5.6. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-1}=0, P_{-2}>0$
, and
$P_{-1}=0, P_{-2}>0$
, and
![]() $r_{\max }\leq 13$
, then
$r_{\max }\leq 13$
, then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
.
$m\geq 56$
.
Proof. Keep the setting in Notation 3.1. By Proposition 2.2,
![]() $P_{-6}\geq 2$
and
$P_{-6}\geq 2$
and
![]() $-K_X^3\geq \frac {1}{70}$
. We always take
$-K_X^3\geq \frac {1}{70}$
. We always take
![]() $\nu _0=2$
.
$\nu _0=2$
.
If
![]() $P_{-4}=1$
, then
$P_{-4}=1$
, then
![]() $P_{-2}=1$
. Following the second paragraph of [Reference Chen and Jiang5, Case IV of Proof of Th. 1.8] (see Table A.2 in the Appendix), we have
$P_{-2}=1$
. Following the second paragraph of [Reference Chen and Jiang5, Case IV of Proof of Th. 1.8] (see Table A.2 in the Appendix), we have
![]() $r_X\leq 130$
. By Corollary 4.9 (with
$r_X\leq 130$
. By Corollary 4.9 (with
![]() $l=1, t=5.5$
, and
$l=1, t=5.5$
, and
![]() $-K_X^3\geq \frac {1}{70}$
),
$-K_X^3\geq \frac {1}{70}$
),
![]() $P_{-24}-1>24$
. If
$P_{-24}-1>24$
. If
![]() $|-24K_X|$
and
$|-24K_X|$
and
![]() $|-6K_X|$
are not composed with the same pencil, then take
$|-6K_X|$
are not composed with the same pencil, then take
![]() $m_1=24$
and
$m_1=24$
and
![]() $\mu _0'=m_0=6$
. Then, by Theorem 3.4(2),
$\mu _0'=m_0=6$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
. If
$m\geq 56$
. If
![]() $|-24K_X|$
and
$|-24K_X|$
and
![]() $|-6K_X|$
are composed with the same pencil, then take
$|-6K_X|$
are composed with the same pencil, then take
![]() $m_0=6$
and
$m_0=6$
and
![]() $\mu _0'=\frac {24}{P_{-24}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
$\mu _0'=\frac {24}{P_{-24}-1}<1$
by Remark 3.2. By Proposition 4.8(1) (with
![]() $t=6.9$
), we can take
$t=6.9$
), we can take
![]() $m_1=30$
. Then, by Theorem 3.4(2),
$m_1=30$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
.
$m\geq 56$
.
From now on, we assume that
![]() $P_{-4}\geq 2$
. Note that
$P_{-4}\geq 2$
. Note that
![]() $-K_X^3\geq \frac {1}{30}$
by Proposition 2.2(3). By Corollary 4.9 (with
$-K_X^3\geq \frac {1}{30}$
by Proposition 2.2(3). By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=3.6$
),
$t=3.6$
),
![]() $P_{-16}-1>16$
. If
$P_{-16}-1>16$
. If
![]() $|-16K_X|$
and
$|-16K_X|$
and
![]() $|-4K_X|$
are not composed with the same pencil, then take
$|-4K_X|$
are not composed with the same pencil, then take
![]() $m_1=16$
and
$m_1=16$
and
![]() $\mu _0'=m_0=4$
. Then, by Theorem 3.4(2),
$\mu _0'=m_0=4$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 46$
.
$m\geq 46$
.
In the following discussions, we assume that
![]() $|-16K_X|$
and
$|-16K_X|$
and
![]() $|-4K_X|$
are composed with the same pencil. We can always take
$|-4K_X|$
are composed with the same pencil. We can always take
![]() $m_0=4$
and
$m_0=4$
and
![]() $\mu _0'=\frac {16}{P_{-16}-1}<1$
by Remark 3.2.
$\mu _0'=\frac {16}{P_{-16}-1}<1$
by Remark 3.2.
Case 1.
![]() $r_{\max }\leq 6$
or
$r_{\max }\leq 6$
or
![]() $r_{\max }\in \{10, 12\}$
.
$r_{\max }\in \{10, 12\}$
.
If
![]() $r_{\max }\leq 6$
, then
$r_{\max }\leq 6$
, then
![]() $r_X\leq 60$
. If
$r_X\leq 60$
. If
![]() $r_{\max }=10$
(resp.
$r_{\max }=10$
(resp.
![]() $r_{\max }=12$
), then
$r_{\max }=12$
), then
![]() $r_X\leq 210$
(resp.
$r_X\leq 210$
(resp.
![]() $r_X\leq 84$
) by [Reference Chen and Jiang5, p. 107]. Then, by Corollary 3.7(2),
$r_X\leq 84$
) by [Reference Chen and Jiang5, p. 107]. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
Case 2.
![]() $r_{\max }=7$
.
$r_{\max }=7$
.
If
![]() $r_{\max }=7$
, then
$r_{\max }=7$
, then
![]() $r_X$
divides
$r_X$
divides
![]() ${\text {lcm}}(2, 3, 4, 5, 6, 7)=420$
. Hence, either
${\text {lcm}}(2, 3, 4, 5, 6, 7)=420$
. Hence, either
![]() $r_X=420$
or
$r_X=420$
or
![]() $r_X\leq 210$
. If
$r_X\leq 210$
. If
![]() $r_X=420$
, then
$r_X=420$
, then
![]() $\{4, 5, 7\}\subset \mathcal {R}_X$
and one element of
$\{4, 5, 7\}\subset \mathcal {R}_X$
and one element of
![]() $\{3, 6\}$
is in
$\{3, 6\}$
is in
![]() $\mathcal {R}_X$
. Suppose that
$\mathcal {R}_X$
. Suppose that
where
![]() $r\in \{3, 6\}$
,
$r\in \{3, 6\}$
,
![]() $a_5\leq 2$
, and
$a_5\leq 2$
, and
![]() $a_7\leq 3$
. Then
$a_7\leq 3$
. Then
![]() $\sigma (B_X)\geq 11$
implies that
$\sigma (B_X)\geq 11$
implies that
![]() $\sum _{i=1}^kb_i\geq 4$
. Lemma 2.3 implies that
$\sum _{i=1}^kb_i\geq 4$
. Lemma 2.3 implies that
 $$ \begin{align} \gamma(B_X)\leq 24-\left(7-\frac{1}{7}+5-\frac{1}{5}+4-\frac{1}{4}+3-\frac{1}{3}+4\times \frac{3}{2}\right)<0, \end{align} $$
$$ \begin{align} \gamma(B_X)\leq 24-\left(7-\frac{1}{7}+5-\frac{1}{5}+4-\frac{1}{4}+3-\frac{1}{3}+4\times \frac{3}{2}\right)<0, \end{align} $$
a contradiction. Hence,
![]() $r_X\leq 210$
. Then, by Corollary 3.7(2),
$r_X\leq 210$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 43$
.
$m\geq 43$
.
Case 3.
![]() $r_{\max }=8$
.
$r_{\max }=8$
.
If
![]() $r_{\max }=8$
, then we claim that
$r_{\max }=8$
, then we claim that
![]() $r_X\leq 168$
. In fact, if
$r_X\leq 168$
. In fact, if
![]() $r_X>168$
, then
$r_X>168$
, then
![]() $\{5, 7\}\subset \mathcal {R}_X$
. Suppose that
$\{5, 7\}\subset \mathcal {R}_X$
. Suppose that
where
![]() $a_5\leq 2$
,
$a_5\leq 2$
,
![]() $a_7\leq 3$
, and
$a_7\leq 3$
, and
![]() $a_8\leq 3$
. Then
$a_8\leq 3$
. Then
![]() $\sigma (B_X)\geq 11$
implies that
$\sigma (B_X)\geq 11$
implies that
![]() $\sum _{i=1}^kb_i\geq 3$
. Similar to (5.2), Lemma 2.3 implies that
$\sum _{i=1}^kb_i\geq 3$
. Similar to (5.2), Lemma 2.3 implies that
![]() $\gamma (B_X)<0$
, a contradiction. Hence,
$\gamma (B_X)<0$
, a contradiction. Hence,
![]() $r_X\leq 168$
.
$r_X\leq 168$
.
Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 43$
.
$m\geq 43$
.
Case 4.
![]() $r_{\max }=9$
.
$r_{\max }=9$
.
If
![]() $r_{\max }=9$
, then we claim that
$r_{\max }=9$
, then we claim that
![]() $r_X\leq 252$
or
$r_X\leq 252$
or
![]() $B_X=\{2\times (1, 2), (2, 5), (3, 7)$
,
$B_X=\{2\times (1, 2), (2, 5), (3, 7)$
,
![]() $(4, 9)\}$
.
$(4, 9)\}$
.
If
![]() $7$
and
$7$
and
![]() $8$
are not in
$8$
are not in
![]() $\mathcal {R}_X$
, then
$\mathcal {R}_X$
, then
![]() $r_X\leq 180$
.
$r_X\leq 180$
.
If
![]() $8\in \mathcal {R}_X$
, then as
$8\in \mathcal {R}_X$
, then as
![]() $\{2, 8, 9\}\subset \mathcal {R}_X$
, we know that
$\{2, 8, 9\}\subset \mathcal {R}_X$
, we know that
![]() $6$
and
$6$
and
![]() $7$
are not in
$7$
are not in
![]() $\mathcal {R}_X$
by
$\mathcal {R}_X$
by
![]() $\gamma (B_X)\geq 0$
. If
$\gamma (B_X)\geq 0$
. If
![]() $5\not \in \mathcal {R}_X$
, then
$5\not \in \mathcal {R}_X$
, then
![]() $r_X= 72$
. If
$r_X= 72$
. If
![]() $5 \in \mathcal {R}_X$
, then
$5 \in \mathcal {R}_X$
, then
![]() $ \mathcal {R}_X=\{2, 5, 8, 9\}$
as
$ \mathcal {R}_X=\{2, 5, 8, 9\}$
as
![]() $\gamma (B_X)\geq 0$
, but in this case,
$\gamma (B_X)\geq 0$
, but in this case,
![]() $\sigma (B_X)\leq 10$
, a contradiction.
$\sigma (B_X)\leq 10$
, a contradiction.
If
![]() $7\in \mathcal {R}_X$
, then as
$7\in \mathcal {R}_X$
, then as
![]() $\{2, 7, 9\}\subset \mathcal {R}_X$
, we know that at most one element of
$\{2, 7, 9\}\subset \mathcal {R}_X$
, we know that at most one element of
![]() $\{4, 5, 6\}$
is in
$\{4, 5, 6\}$
is in
![]() $\mathcal {R}_X$
by
$\mathcal {R}_X$
by
![]() $\gamma (B_X)\geq 0$
. If
$\gamma (B_X)\geq 0$
. If
![]() $5\not \in \mathcal {R}_X$
, then
$5\not \in \mathcal {R}_X$
, then
![]() $r_X\leq 252$
. If
$r_X\leq 252$
. If
![]() $5 \in \mathcal {R}_X$
, then by
$5 \in \mathcal {R}_X$
, then by
![]() $\sigma (B_X)\geq 11$
and
$\sigma (B_X)\geq 11$
and
![]() $\gamma (B_X)\geq 0$
, it is not hard to check that the only possible basket is
$\gamma (B_X)\geq 0$
, it is not hard to check that the only possible basket is
![]() $B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
. This concludes the claim.
$B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
. This concludes the claim.
If
![]() $r_X\leq 252$
, then by Corollary 3.7(2),
$r_X\leq 252$
, then by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 50$
.
$m\geq 50$
.
If
![]() $B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
, then
$B_X=\{2\times (1, 2), (2, 5), (3, 7), (4, 9)\}$
, then
![]() $-K_X^3=\frac {43}{315}$
. By Proposition 4.8(2) (with
$-K_X^3=\frac {43}{315}$
. By Proposition 4.8(2) (with
![]() $t=7.6$
), we can take
$t=7.6$
), we can take
![]() $m_1=23$
. Then, by Theorem 3.4(2),
$m_1=23$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 41$
.
$m\geq 41$
.
Case 5.
![]() $r_{\max }=11$
.
$r_{\max }=11$
.
If
![]() $r_{\max }=11$
, then we claim that
$r_{\max }=11$
, then we claim that
![]() $r_X\leq 264$
or
$r_X\leq 264$
or
![]() $B_X=\{3\times (1, 2), (1, 3), (2, 5)$
,
$B_X=\{3\times (1, 2), (1, 3), (2, 5)$
,
![]() $(5, 11)\}$
or
$(5, 11)\}$
or
![]() $B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
.
$B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
.
As
![]() $\{2, 11\}\subset \mathcal {R}_X$
, we know that at most one element of
$\{2, 11\}\subset \mathcal {R}_X$
, we know that at most one element of
![]() $\{6, 7, 8, 9, 10\}$
is in
$\{6, 7, 8, 9, 10\}$
is in
![]() $\mathcal {R}_X$
by
$\mathcal {R}_X$
by
![]() $\gamma (B_X)\geq 0$
. If
$\gamma (B_X)\geq 0$
. If
![]() $10\in \mathcal {R}_X$
, then
$10\in \mathcal {R}_X$
, then
![]() $r_X= 110$
by [Reference Chen and Jiang5, p. 107]. If
$r_X= 110$
by [Reference Chen and Jiang5, p. 107]. If
![]() $9\in \mathcal {R}_X$
or
$9\in \mathcal {R}_X$
or
![]() $8\in \mathcal {R}_X$
, then
$8\in \mathcal {R}_X$
, then
![]() $r_X\leq 264$
by [Reference Chen and Jiang5, p. 107]. If
$r_X\leq 264$
by [Reference Chen and Jiang5, p. 107]. If
![]() $7\in \mathcal {R}_X$
, then
$7\in \mathcal {R}_X$
, then
![]() $5\not \in \mathcal {R}_X$
by
$5\not \in \mathcal {R}_X$
by
![]() $\gamma (B_X)\geq 0$
. So either
$\gamma (B_X)\geq 0$
. So either
![]() $r_X=154$
or at least one element of
$r_X=154$
or at least one element of
![]() $\{3, 4\}$
is in
$\{3, 4\}$
is in
![]() $\mathcal {R}_X$
. For the latter case, it is not hard to check that the only basket satisfying
$\mathcal {R}_X$
. For the latter case, it is not hard to check that the only basket satisfying
![]() $\sigma (B_X)\geq 11$
and
$\sigma (B_X)\geq 11$
and
![]() $\gamma (B_X)\geq 0$
is
$\gamma (B_X)\geq 0$
is
![]() $B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
. If
$B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
. If
![]() $6\in \mathcal {R}_X$
, then we get a contradiction by Lemma 2.3 as (5.2).
$6\in \mathcal {R}_X$
, then we get a contradiction by Lemma 2.3 as (5.2).
If none element of
![]() $\{6, 7, 8, 9, 10\}$
is in
$\{6, 7, 8, 9, 10\}$
is in
![]() $\mathcal {R}_X$
, then
$\mathcal {R}_X$
, then
![]() $r_X$
divides
$r_X$
divides
![]() $660$
and
$660$
and
![]() $r_X<660$
by [Reference Chen and Jiang5, p. 107]. So either
$r_X<660$
by [Reference Chen and Jiang5, p. 107]. So either
![]() $r_X\leq 220$
or
$r_X\leq 220$
or
![]() $r_X=330$
. Moreover, if
$r_X=330$
. Moreover, if
![]() $r_X=330$
, then
$r_X=330$
, then
![]() $\{2, 3, 5, 11\}\subset \mathcal {R}_X$
and
$\{2, 3, 5, 11\}\subset \mathcal {R}_X$
and
![]() $4\not \in \mathcal {R}_X$
, and it is not hard to check that the only basket satisfying
$4\not \in \mathcal {R}_X$
, and it is not hard to check that the only basket satisfying
![]() $\sigma (B_X)\geq 11$
and
$\sigma (B_X)\geq 11$
and
![]() $\gamma (B_X)\geq 0$
is
$\gamma (B_X)\geq 0$
is
![]() $B_X=\{3\times (1, 2), (1, 3), (2, 5), (5, 11)\}$
. This concludes the claim.
$B_X=\{3\times (1, 2), (1, 3), (2, 5), (5, 11)\}$
. This concludes the claim.
If
![]() $r_X\leq 264$
, then by Corollary 3.7(2),
$r_X\leq 264$
, then by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
.
$m\geq 56$
.
If
![]() $B_X=\{3\times (1, 2), (1, 3), (2, 5), (5, 11)\}$
, then
$B_X=\{3\times (1, 2), (1, 3), (2, 5), (5, 11)\}$
, then
![]() $-K_X^3=\frac {31}{330}$
. By Proposition 4.8(2) (with
$-K_X^3=\frac {31}{330}$
. By Proposition 4.8(2) (with
![]() $t=7.6$
), we can take
$t=7.6$
), we can take
![]() $m_1=28$
. Then, by Theorem 3.4(2),
$m_1=28$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 50$
.
$m\geq 50$
.
If
![]() $B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
, then
$B_X=\{2\times (1, 2), (1, 3), (3, 7), (5, 11)\}$
, then
![]() $-K_X^3=\frac {50}{462}$
. By Proposition 4.8(2) (with
$-K_X^3=\frac {50}{462}$
. By Proposition 4.8(2) (with
![]() $t=7$
), we can take
$t=7$
), we can take
![]() $m_1=26$
. Then, by Theorem 3.4(2),
$m_1=26$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
Case 6.
![]() $r_{\max }=13$
.
$r_{\max }=13$
.
If
![]() $r_{\max }=13$
, then
$r_{\max }=13$
, then
![]() $r_X\leq 390$
or
$r_X\leq 390$
or
![]() $r_X=546$
by [Reference Chen and Jiang5, p. 107].
$r_X=546$
by [Reference Chen and Jiang5, p. 107].
If
![]() $r_X=546$
, then again by [Reference Chen and Jiang5, p. 107],
$r_X=546$
, then again by [Reference Chen and Jiang5, p. 107],
![]() $B_X=\{(1, 2), (1, 3), (3, 7), (6, 13)\}$
and
$B_X=\{(1, 2), (1, 3), (3, 7), (6, 13)\}$
and
![]() $-K_X^3=\frac {61}{546}$
. By Proposition 4.8(2) (with
$-K_X^3=\frac {61}{546}$
. By Proposition 4.8(2) (with
![]() $t=6$
), we can take
$t=6$
), we can take
![]() $m_1=26$
. Then, by Theorem 3.4(2),
$m_1=26$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
If
![]() $r_X\leq 390$
and
$r_X\leq 390$
and
![]() $-K_X^3\geq \frac {1}{12}$
, then by Proposition 4.8(2) (with
$-K_X^3\geq \frac {1}{12}$
, then by Proposition 4.8(2) (with
![]() $t=6.9$
), we can take
$t=6.9$
), we can take
![]() $m_1=30$
. Then, by Theorem 3.4(2),
$m_1=30$
. Then, by Theorem 3.4(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
.
$m\geq 56$
.
If
![]() $r_X\leq 390$
and
$r_X\leq 390$
and
![]() $-K_X^3<\frac {1}{12}$
, then by Lemma 5.5,
$-K_X^3<\frac {1}{12}$
, then by Lemma 5.5,
![]() $B_X$
is dominated by
$B_X$
is dominated by
![]() $\{8\times (1, 2), 3\times (1, 3)\}$
. As
$\{8\times (1, 2), 3\times (1, 3)\}$
. As
![]() $r_{\max }=13$
, this implies that
$r_{\max }=13$
, this implies that
![]() $B_X$
is dominated by either
$B_X$
is dominated by either
![]() $\{3\times (1, 2), (6, 13), 2\times (1, 3)\}$
or
$\{3\times (1, 2), (6, 13), 2\times (1, 3)\}$
or
![]() $\{6\times (1, 2), (5, 13)\}$
. So we get the following possibilities of
$\{6\times (1, 2), (5, 13)\}$
. So we get the following possibilities of
![]() $B_X$
by
$B_X$
by
![]() $\gamma (B_X)\geq 0$
:
$\gamma (B_X)\geq 0$
:
 $$ \begin{align*} {}& \{3\times(1, 2), (6, 13), 2\times(1, 3)\} &{}-K^3=5/78,\\ {}& \{2\times(1, 2), (6, 13), (2, 5), (1, 3)\}&{}-K^3=19/195,\\ {}& \{2\times(1, 2), (6, 13), (3, 8)\}&{}-K^3=11/104,\\ {}& \{(1, 2), (6, 13), (3, 7), (1, 3)\}&{}-K^3=61/546,\\ {}& \{6\times(1, 2), (5, 13)\}&{}-K^3= 1/13. \end{align*} $$
$$ \begin{align*} {}& \{3\times(1, 2), (6, 13), 2\times(1, 3)\} &{}-K^3=5/78,\\ {}& \{2\times(1, 2), (6, 13), (2, 5), (1, 3)\}&{}-K^3=19/195,\\ {}& \{2\times(1, 2), (6, 13), (3, 8)\}&{}-K^3=11/104,\\ {}& \{(1, 2), (6, 13), (3, 7), (1, 3)\}&{}-K^3=61/546,\\ {}& \{6\times(1, 2), (5, 13)\}&{}-K^3= 1/13. \end{align*} $$
In the above list, only the first and the last have
![]() $-K_X^3<\frac {1}{12}$
. In particular, in these cases,
$-K_X^3<\frac {1}{12}$
. In particular, in these cases,
![]() $r_X\leq 78$
. Then, by Corollary 3.7(2),
$r_X\leq 78$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 55$
.
$m\geq 55$
.
Combining all above cases, we have proved the theorem.
5.4 The case
 $P_{-1}>0$
$P_{-1}>0$
Lemma 5.7. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-1}>0$
and
$P_{-1}>0$
and
![]() $r_{\max }\geq 16$
, then
$r_{\max }\geq 16$
, then
![]() $P_{-4}\geq 2$
.
$P_{-4}\geq 2$
.
Proof. If
![]() $P_{-4}=1$
, then
$P_{-4}=1$
, then
![]() $P_{-2}=P_{-3}=1$
. Since
$P_{-2}=P_{-3}=1$
. Since
![]() $r_{\max }\geq 16$
, by the classification in [Reference Chen and Chen2, Subsubcase II-4f of Proof of Th. 4.4],
$r_{\max }\geq 16$
, by the classification in [Reference Chen and Chen2, Subsubcase II-4f of Proof of Th. 4.4],
![]() $B_X$
is dominated by
$B_X$
is dominated by
![]() $\{2\times (1, 2), 2\times (1, 3), (1, s_1), (1, s_2)\}$
with
$\{2\times (1, 2), 2\times (1, 3), (1, s_1), (1, s_2)\}$
with
![]() $s_2\geq s_1\geq 5$
, which means that
$s_2\geq s_1\geq 5$
, which means that
![]() $s_1+s_2=r_{\max }\geq 16$
. But in this case
$s_1+s_2=r_{\max }\geq 16$
. But in this case
![]() $2\times \frac {3}{2}+2\times \frac {8}{3}+16-\frac {1}{16}>24$
, contradicting (2.4) and [Reference Chen and Chen2, Lem. 3.1]. So
$2\times \frac {3}{2}+2\times \frac {8}{3}+16-\frac {1}{16}>24$
, contradicting (2.4) and [Reference Chen and Chen2, Lem. 3.1]. So
![]() $P_{-4}\geq 2$
.
$P_{-4}\geq 2$
.
Theorem 5.8. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-1}>0$
and
$P_{-1}>0$
and
![]() $r_{\max } \geq 14$
, then
$r_{\max } \geq 14$
, then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
Proof. Keep the setting in Notation 3.1. We always take
![]() $\nu _0=1$
.
$\nu _0=1$
.
If
![]() $14\leq r_{\max } \leq 15$
, then
$14\leq r_{\max } \leq 15$
, then
![]() $r_X\leq 210$
by [Reference Chen and Jiang5, p. 104]. By Proposition 2.2(2), we can take
$r_X\leq 210$
by [Reference Chen and Jiang5, p. 104]. By Proposition 2.2(2), we can take
![]() $\mu _{0}'=m_0=8$
. Then, by Corollary 3.7(2),
$\mu _{0}'=m_0=8$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
If
![]() $r_{\max }=24$
, then
$r_{\max }=24$
, then
![]() $B_X=\{(b, 24)\}$
with
$B_X=\{(b, 24)\}$
with
![]() $b\in \{1, 5, 7, 11\}$
. If
$b\in \{1, 5, 7, 11\}$
. If
![]() $P_{-1}=1$
, then
$P_{-1}=1$
, then
![]() $b=\sigma (B_X)=5+P_{-2}\geq 6$
by (2.3); hence,
$b=\sigma (B_X)=5+P_{-2}\geq 6$
by (2.3); hence,
![]() $b\geq 7$
and
$b\geq 7$
and
![]() $P_{-2}\geq 2$
. By (2.2), we have
$P_{-2}\geq 2$
. By (2.2), we have
![]() $-K_X^3\geq \frac {23}{24}$
. Similarly, if
$-K_X^3\geq \frac {23}{24}$
. Similarly, if
![]() $P_{-1}=2$
, then
$P_{-1}=2$
, then
![]() $P_{-2}\geq 2P_{-1}-1=3$
, and thus
$P_{-2}\geq 2P_{-1}-1=3$
, and thus
![]() $b\geq 5$
. Hence, by (2.2),
$b\geq 5$
. Hence, by (2.2),
![]() $-K_X^3\geq \frac {47}{24}$
. If
$-K_X^3\geq \frac {47}{24}$
. If
![]() $P_{-1}\geq 3$
, then by (2.2),
$P_{-1}\geq 3$
, then by (2.2),
![]() $-K_X^3\geq b-\frac {b^2}{24}\geq \frac {23}{24}$
. In summary,
$-K_X^3\geq b-\frac {b^2}{24}\geq \frac {23}{24}$
. In summary,
![]() $-K_X^3\geq \frac {23}{24}$
and
$-K_X^3\geq \frac {23}{24}$
and
![]() $P_{-2}\geq 2$
. We can take
$P_{-2}\geq 2$
. We can take
![]() $\mu _{0}'=m_0=2$
. By Proposition 4.8(2) (with
$\mu _{0}'=m_0=2$
. By Proposition 4.8(2) (with
![]() $t=1$
), we can take
$t=1$
), we can take
![]() $m_1=9$
. Then, by Theorem 3.4(1),
$m_1=9$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 33$
.
$m\geq 33$
.
In the following, we consider
![]() $16\leq r_{\max }\leq 23$
. By Lemma 5.7, we always take
$16\leq r_{\max }\leq 23$
. By Lemma 5.7, we always take
![]() $\mu _{0}'=m_0=4$
and
$\mu _{0}'=m_0=4$
and
![]() $\nu _0=1$
.
$\nu _0=1$
.
If
![]() $r_{\max }=23$
, then
$r_{\max }=23$
, then
![]() $B_X=\{(b, 23)\}$
with
$B_X=\{(b, 23)\}$
with
![]() $1\leq b\leq 11$
. If
$1\leq b\leq 11$
. If
![]() $P_{-1}=1$
, then
$P_{-1}=1$
, then
![]() $b=5+P_{-2}\geq 6$
and thus by (2.2)
$b=5+P_{-2}\geq 6$
and thus by (2.2)
![]() $-K_X^3\geq \frac {10}{23}$
. If
$-K_X^3\geq \frac {10}{23}$
. If
![]() $P_{-1}=2$
, then
$P_{-1}=2$
, then
![]() $b=P_{-2}\geq 2P_{-1}-1=3$
; hence, by (2.2)
$b=P_{-2}\geq 2P_{-1}-1=3$
; hence, by (2.2)
![]() $-K_X^3\geq \frac {14}{23}$
. If
$-K_X^3\geq \frac {14}{23}$
. If
![]() $P_{-1}\geq 3$
, then
$P_{-1}\geq 3$
, then
![]() $-K_X^3\geq b-\frac {b^2}{23}\geq \frac {22}{23}$
. In summary,
$-K_X^3\geq b-\frac {b^2}{23}\geq \frac {22}{23}$
. In summary,
![]() $-K_X^3\geq \frac {10}{23}$
. By Proposition 4.8(1) (with
$-K_X^3\geq \frac {10}{23}$
. By Proposition 4.8(1) (with
![]() $t=\frac {36}{23}$
), we can take
$t=\frac {36}{23}$
), we can take
![]() $m_1=12$
. Then, by Theorem 3.4(1),
$m_1=12$
. Then, by Theorem 3.4(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
If
![]() $20\leq r_{\max } \leq 22$
, then by (2.4), we have
$20\leq r_{\max } \leq 22$
, then by (2.4), we have
![]() $r_X\leq 60$
. Then, by Corollary 3.7(2),
$r_X\leq 60$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 50$
.
$m\geq 50$
.
If
![]() $18\leq r_{\max } \leq 19$
, then
$18\leq r_{\max } \leq 19$
, then
![]() $r_X\leq 190$
by [Reference Chen and Jiang5, p. 104]. Then, by Corollary 3.7(2),
$r_X\leq 190$
by [Reference Chen and Jiang5, p. 104]. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
If
![]() $16\leq r_{\max } \leq 17$
, then
$16\leq r_{\max } \leq 17$
, then
![]() $r_X\leq 240$
by [Reference Chen and Jiang5, p. 104]. Then, by Corollary 3.7(2),
$r_X\leq 240$
by [Reference Chen and Jiang5, p. 104]. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
.
$m\geq 52$
.
Theorem 5.9. Let X be a terminal weak
![]() ${\mathbb {Q}}$
-Fano threefold. If
${\mathbb {Q}}$
-Fano threefold. If
![]() $P_{-1}>0$
and
$P_{-1}>0$
and
![]() $r_{\max }\leq 13$
, then
$r_{\max }\leq 13$
, then
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 58$
.
$m\geq 58$
.
Proof. Keep the setting in Notation 3.1. By Theorem 5.1 and Proposition 2.2(1), we may assume that
![]() $r_X\leq 660$
. By Proposition 2.2(2), we can take
$r_X\leq 660$
. By Proposition 2.2(2), we can take
![]() $m_0=8$
and
$m_0=8$
and
![]() $\nu _0=1$
. We take
$\nu _0=1$
. We take
![]() $\mu _0'=8$
unless stated otherwise.
$\mu _0'=8$
unless stated otherwise.
Case 1.
![]() $r_{\max }\leq 8$
.
$r_{\max }\leq 8$
.
If
![]() $r_{\max }\leq 8$
, then
$r_{\max }\leq 8$
, then
![]() $r_{X}$
divides
$r_{X}$
divides
![]() ${\text {lcm}}(8, 7, 6, 5)=840$
. As
${\text {lcm}}(8, 7, 6, 5)=840$
. As
![]() $r_{X}\leq 660$
,
$r_{X}\leq 660$
,
![]() $r_X=420$
or
$r_X=420$
or
![]() $r_X\leq 280$
.
$r_X\leq 280$
.
If
![]() $r_X=420$
, then by Proposition 4.8(1) (with
$r_X=420$
, then by Proposition 4.8(1) (with
![]() $t=19.5$
,
$t=19.5$
,
![]() $-K_X^3\geq \frac {1}{330}$
), we can take
$-K_X^3\geq \frac {1}{330}$
), we can take
![]() $m_1=52$
. By Lemma 3.3,
$m_1=52$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {420}{8m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
$N_0\geq \lceil \frac {420}{8m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
If
![]() $r_X\leq 280$
, then by Corollary 3.7(1),
$r_X\leq 280$
, then by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 55$
.
$m\geq 55$
.
Case 2.
![]() $r_{\max }=9$
.
$r_{\max }=9$
.
If
![]() $r_{\max }=9$
, then
$r_{\max }=9$
, then
![]() $r_X$
divides
$r_X$
divides
![]() $2,520$
. As
$2,520$
. As
![]() $r_X\leq 660$
and
$r_X\leq 660$
and
![]() $9$
divides
$9$
divides
![]() $r_X$
, we have
$r_X$
, we have
![]() $r_X\leq 360$
or
$r_X\leq 360$
or
![]() $r_X\in \{504, 630\}$
.
$r_X\in \{504, 630\}$
.
If
![]() $r_X\leq 360$
, then by Corollary 4.9 (with
$r_X\leq 360$
, then by Corollary 4.9 (with
![]() $l=4, t=10$
, and
$l=4, t=10$
, and
![]() $-K_X^3\geq \frac {1}{330}$
), we have
$-K_X^3\geq \frac {1}{330}$
), we have
![]() $P_{-30}-1>\frac {30}{4}$
. If
$P_{-30}-1>\frac {30}{4}$
. If
![]() $|-30K_X|$
and
$|-30K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {30}{P_{-30}-1}<4$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {30}{P_{-30}-1}<4$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 57$
. If
$m\geq 57$
. If
![]() $|-30K_X|$
and
$|-30K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=30$
and
$m_1=30$
and
![]() $\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
$\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
.
$m\geq 56$
.
If
![]() $r_X=630$
, then
$r_X=630$
, then
![]() $-K_X^3\geq \frac {1}{315}$
(note that
$-K_X^3\geq \frac {1}{315}$
(note that
![]() $-K_X^3\geq \frac {1}{330}$
and
$-K_X^3\geq \frac {1}{330}$
and
![]() $r_X(-K_X^3)$
is an integer). By Corollary 4.9 (with
$r_X(-K_X^3)$
is an integer). By Corollary 4.9 (with
![]() $l=2.8$
and
$l=2.8$
and
![]() $t=11$
), we have
$t=11$
), we have
![]() $P_{-33}-1>\frac {33}{2.8}$
. If
$P_{-33}-1>\frac {33}{2.8}$
. If
![]() $|-33K_X|$
and
$|-33K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {33}{P_{-33}-1}<2.8$
by Remark 3.2. By Proposition 4.8(1) (with
$\mu _0'=\frac {33}{P_{-33}-1}<2.8$
by Remark 3.2. By Proposition 4.8(1) (with
![]() $t=20$
and
$t=20$
and
![]() $-K_X^3\geq \frac {1}{315}$
), we can take
$-K_X^3\geq \frac {1}{315}$
), we can take
![]() $m_1=63$
. By Lemma 3.3,
$m_1=63$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {630}{9m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
$N_0\geq \lceil \frac {630}{9m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
. If
$m\geq 52$
. If
![]() $|-33K_X|$
and
$|-33K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=33$
and
$m_1=33$
and
![]() $\mu _0'=m_0=8$
. By Lemma 3.3,
$\mu _0'=m_0=8$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {630}{9m_{1}}\rceil =3$
. Then, by Corollary 3.7(1),
$N_0\geq \lceil \frac {630}{9m_{1}}\rceil =3$
. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
If
![]() $r_X=504$
, then
$r_X=504$
, then
![]() $\mathcal {R}_X=\{9, 8, 7\}$
by (2.4). Write
$\mathcal {R}_X=\{9, 8, 7\}$
by (2.4). Write
![]() $B_X=\{(a, 7), (b, 8), (c, 9)\}$
, where
$B_X=\{(a, 7), (b, 8), (c, 9)\}$
, where
![]() $a\leq 3, b\in \{1, 3\}$
and
$a\leq 3, b\in \{1, 3\}$
and
![]() $c\in \{1, 2, 4\}$
. If
$c\in \{1, 2, 4\}$
. If
![]() $P_{-1}\geq 2$
, then by (2.2),
$P_{-1}\geq 2$
, then by (2.2),
 $$ \begin{align} -K_X^{3}{}&=2P_{-1}+\frac{a(7-a)}{7}+\frac{b(8-b)}{8}+\frac{c(9-c)}{9}-6\notag\\ {}&\geq \frac{6}{7}+\frac{7}{8}+\frac{8}{9}-2>0.6. \end{align} $$
$$ \begin{align} -K_X^{3}{}&=2P_{-1}+\frac{a(7-a)}{7}+\frac{b(8-b)}{8}+\frac{c(9-c)}{9}-6\notag\\ {}&\geq \frac{6}{7}+\frac{7}{8}+\frac{8}{9}-2>0.6. \end{align} $$
If
![]() $P_{-1}=1$
, then by (2.2) and (2.3),
$P_{-1}=1$
, then by (2.2) and (2.3),
 $$ \begin{align} -K_X^{3}{}&=\frac{a(7-a)}{7}+\frac{b(8-b)}{8}+\frac{c(9-c)}{9}-4>0,\notag\\ \sigma(B_X){}&=a+b+c=5+P_{-2}\geq6. \end{align} $$
$$ \begin{align} -K_X^{3}{}&=\frac{a(7-a)}{7}+\frac{b(8-b)}{8}+\frac{c(9-c)}{9}-4>0,\notag\\ \sigma(B_X){}&=a+b+c=5+P_{-2}\geq6. \end{align} $$
So it is easy to check that
![]() $-K_X^3\geq \frac {73}{504}$
by considering all possible values of
$-K_X^3\geq \frac {73}{504}$
by considering all possible values of
![]() $(a, b, c)$
. By Proposition 4.8(2) (with
$(a, b, c)$
. By Proposition 4.8(2) (with
![]() $t=7.3$
and
$t=7.3$
and
![]() $-K_X^3\geq \frac {73}{504}$
), we can take
$-K_X^3\geq \frac {73}{504}$
), we can take
![]() $m_1=22$
. By Lemma 3.3,
$m_1=22$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {504}{9m_{1}}\rceil =3$
. Then, by Corollary 3.7(1),
$N_0\geq \lceil \frac {504}{9m_{1}}\rceil =3$
. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 44$
.
$m\geq 44$
.
Case 3.
![]() $r_{\max }=10$
.
$r_{\max }=10$
.
If
![]() $r_{\max }=10$
, then we claim that
$r_{\max }=10$
, then we claim that
![]() $r_X\leq 210$
or
$r_X\leq 210$
or
![]() $r_X=420$
.
$r_X=420$
.
By (2.4), at most one element of
![]() $\{7, 8, 9\}$
is in
$\{7, 8, 9\}$
is in
![]() $\mathcal {R}_X$
. If
$\mathcal {R}_X$
. If
![]() $7\not \in \mathcal {R}_X$
, then
$7\not \in \mathcal {R}_X$
, then
![]() $r_X$
divides either
$r_X$
divides either
![]() $120={\text {lcm}}(10, 8, 60)$
or
$120={\text {lcm}}(10, 8, 60)$
or
![]() $180={\text {lcm}}(10, 9, 60)$
. If
$180={\text {lcm}}(10, 9, 60)$
. If
![]() $7 \in \mathcal {R}_X$
, then
$7 \in \mathcal {R}_X$
, then
![]() $r_X$
divides
$r_X$
divides
![]() $420={\text {lcm}}(10, 7, 60)$
, so either
$420={\text {lcm}}(10, 7, 60)$
, so either
![]() $r_X\leq 210$
or
$r_X\leq 210$
or
![]() $r_X=420$
. This concludes the claim.
$r_X=420$
. This concludes the claim.
If
![]() $r_X\leq 210$
, then by Corollary 3.7(1),
$r_X\leq 210$
, then by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 48$
.
$m\geq 48$
.
If
![]() $r_X=420$
, then by (2.4),
$r_X=420$
, then by (2.4),
![]() $\mathcal {R}_X=\{10, 7, 4, 3\}$
. Write
$\mathcal {R}_X=\{10, 7, 4, 3\}$
. Write
![]() $B_X=\{(1, 3), (1, 4)$
,
$B_X=\{(1, 3), (1, 4)$
,
![]() $(a, 7), (b, 10)\}$
, where
$(a, 7), (b, 10)\}$
, where
![]() $a\leq 3$
and
$a\leq 3$
and
![]() $b\in \{1, 3\}$
. If
$b\in \{1, 3\}$
. If
![]() $P_{-1}\geq 2$
, then by (2.2),
$P_{-1}\geq 2$
, then by (2.2),
 $$ \begin{align} -K_X^{3}{}&=2P_{-1}+\frac{2}{3}+\frac{3}{4}+\frac{a(7-a)}{7}+\frac{b(10-b)}{10}-6\notag\\ {}&\geq \frac{2}{3}+\frac{3}{4}+\frac{6}{7}+\frac{9}{10}-2>1. \end{align} $$
$$ \begin{align} -K_X^{3}{}&=2P_{-1}+\frac{2}{3}+\frac{3}{4}+\frac{a(7-a)}{7}+\frac{b(10-b)}{10}-6\notag\\ {}&\geq \frac{2}{3}+\frac{3}{4}+\frac{6}{7}+\frac{9}{10}-2>1. \end{align} $$
If
![]() $P_{-1}=1$
, then by (2.2) and (2.3),
$P_{-1}=1$
, then by (2.2) and (2.3),
 $$ \begin{align} -K_X^{3}{}&=\frac{2}{3}+\frac{3}{4}+\frac{a(7-a)}{7}+\frac{b(10-b)}{10}-4>0,\notag\\ \sigma(B_X){}&=2+a+b=5+P_{-2}\geq6. \end{align} $$
$$ \begin{align} -K_X^{3}{}&=\frac{2}{3}+\frac{3}{4}+\frac{a(7-a)}{7}+\frac{b(10-b)}{10}-4>0,\notag\\ \sigma(B_X){}&=2+a+b=5+P_{-2}\geq6. \end{align} $$
So it is easy to check that
![]() $-K_X^3\geq \frac {13}{420}$
by considering all possible values of
$-K_X^3\geq \frac {13}{420}$
by considering all possible values of
![]() $(a, b)$
. By Corollary 4.9 (with
$(a, b)$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=4.8$
), we have
$t=4.8$
), we have
![]() $P_{-16}-1>16$
. If
$P_{-16}-1>16$
. If
![]() $|-16K_X|$
and
$|-16K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {16}{P_{-16}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {16}{P_{-16}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 58$
. If
$m\geq 58$
. If
![]() $|-16K_X|$
and
$|-16K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=16$
and
$m_1=16$
and
![]() $\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
$\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 44$
.
$m\geq 44$
.
Case 4.
![]() $r_{\max }=11$
.
$r_{\max }=11$
.
If
![]() $r_{\max }=11$
, then we claim that
$r_{\max }=11$
, then we claim that
![]() $r_X\leq 330$
or
$r_X\leq 330$
or
![]() $r_X\in \{385, 396, 440, 462, 660\}$
.
$r_X\in \{385, 396, 440, 462, 660\}$
.
By (2.4), at most one element of
![]() $\{7, 8, 9, 10\}$
is in
$\{7, 8, 9, 10\}$
is in
![]() $\mathcal {R}_X$
. So
$\mathcal {R}_X$
. So
![]() $r_X$
divides one element of
$r_X$
divides one element of
![]() $\{1,980, 1,320, 4,620\}$
. As
$\{1,980, 1,320, 4,620\}$
. As
![]() $r_X\leq 660$
and
$r_X\leq 660$
and
![]() $11$
divides
$11$
divides
![]() $r_X$
, it is clear that
$r_X$
, it is clear that
![]() $r_X\leq 330$
or
$r_X\leq 330$
or
![]() $r_X\in \{385, 396, 440, 462, 495, 660\}$
. Moreover, if
$r_X\in \{385, 396, 440, 462, 495, 660\}$
. Moreover, if
![]() $r_X=495$
, then
$r_X=495$
, then
![]() $\{11, 9, 5\}\subset \mathcal {R}_X$
, which contradicts (2.4). This concludes the claim.
$\{11, 9, 5\}\subset \mathcal {R}_X$
, which contradicts (2.4). This concludes the claim.
If
![]() $r_X\leq 330$
, then by Corollary 4.9 (with
$r_X\leq 330$
, then by Corollary 4.9 (with
![]() $l=7.6$
,
$l=7.6$
,
![]() $t=7.6$
, and
$t=7.6$
, and
![]() $-K_X^3\geq \frac {1}{330}$
),
$-K_X^3\geq \frac {1}{330}$
),
![]() $P_{-28}-1>\frac {28}{7.6}$
. If
$P_{-28}-1>\frac {28}{7.6}$
. If
![]() $|-28K_X|$
and
$|-28K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {28}{P_{-28}-1}<7.6$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {28}{P_{-28}-1}<7.6$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 58$
. If
$m\geq 58$
. If
![]() $|-28K_X|$
and
$|-28K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=28$
and
$m_1=28$
and
![]() $\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
$\mu _0'=m_0=8$
. Then, by Theorem 3.4(3),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 58$
.
$m\geq 58$
.
If
![]() $r_X=385$
(resp.
$r_X=385$
(resp.
![]() $396$
), then
$396$
), then
![]() $-K_X^3\geq \frac {2}{385}$
(resp.
$-K_X^3\geq \frac {2}{385}$
(resp.
![]() $\geq \frac {2}{396}$
). By Corollary 4.9 (with
$\geq \frac {2}{396}$
). By Corollary 4.9 (with
![]() $l=1.5$
and
$l=1.5$
and
![]() $t=9$
),
$t=9$
),
![]() $P_{-33}-1>\frac {33}{1.5}$
. If
$P_{-33}-1>\frac {33}{1.5}$
. If
![]() $|-33K_X|$
and
$|-33K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {33}{P_{-33}-1}<1.5$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {33}{P_{-33}-1}<1.5$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
(resp.
$m\geq 56$
(resp.
![]() $\geq 57$
). If
$\geq 57$
). If
![]() $|-33K_X|$
and
$|-33K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=33$
and
$m_1=33$
and
![]() $\mu _0'=m_0=8$
. By Lemma 3.3,
$\mu _0'=m_0=8$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {385}{11m_{1}}\rceil = 2$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {385}{11m_{1}}\rceil = 2$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 47$
(resp.
$m\geq 47$
(resp.
![]() $\geq 48$
).
$\geq 48$
).
We claim that if
![]() $r_X\in \{440, 462, 660\}$
, then
$r_X\in \{440, 462, 660\}$
, then
![]() $-K_X^3\geq \frac {74}{462}$
or
$-K_X^3\geq \frac {74}{462}$
or
![]() $B_X=\{(1, 2), (2, 5), (1,$
$B_X=\{(1, 2), (2, 5), (1,$
![]() $ 3), (1, 4), (1, 11)\}$
with
$ 3), (1, 4), (1, 11)\}$
with
![]() $-K_X^3=\frac {17}{660}$
.
$-K_X^3=\frac {17}{660}$
.
If
![]() $r_X=440$
, then by (2.4),
$r_X=440$
, then by (2.4),
![]() $\mathcal {R}_X=\{11, 8, 5\}$
. Arguing similarly as (5.3), we get
$\mathcal {R}_X=\{11, 8, 5\}$
. Arguing similarly as (5.3), we get
![]() $-K_X^3>0.5$
when
$-K_X^3>0.5$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.4), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.4), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {97}{440}$
.
$-K_X^3\geq \frac {97}{440}$
.
If
![]() $r_X=462$
, then by (2.4),
$r_X=462$
, then by (2.4),
![]() $\mathcal {R}_X=\{11, 7, 6\}$
or
$\mathcal {R}_X=\{11, 7, 6\}$
or
![]() $\{11, 7, 3, 2\}$
or
$\{11, 7, 3, 2\}$
or
![]() $\{11, 7, 3, 2, 2\}$
. Arguing similarly as (5.5), we get
$\{11, 7, 3, 2, 2\}$
. Arguing similarly as (5.5), we get
![]() $-K_X^3>0.5$
or
$-K_X^3>0.5$
or
![]() $-K_X^3>0.9$
or
$-K_X^3>0.9$
or
![]() $-K_X^3>1$
when
$-K_X^3>1$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {85}{462}$
or
$-K_X^3\geq \frac {85}{462}$
or
![]() $-K_X^3\geq \frac {95}{462}$
or
$-K_X^3\geq \frac {95}{462}$
or
![]() $-K_X^3\geq \frac {74}{462}$
unless
$-K_X^3\geq \frac {74}{462}$
unless
![]() $B_X=\{2\times (1, 2), (1, 3), (2, 7), (1, 11)\}$
with
$B_X=\{2\times (1, 2), (1, 3), (2, 7), (1, 11)\}$
with
![]() $-K_X^3=\frac {1}{231}$
. But the last basket has
$-K_X^3=\frac {1}{231}$
. But the last basket has
![]() $P_{-5}=0$
, which is absurd.
$P_{-5}=0$
, which is absurd.
If
![]() $r_X=660$
, then by (2.4),
$r_X=660$
, then by (2.4),
![]() $\mathcal {R}_X=\{11, 5, 4, 3\}$
or
$\mathcal {R}_X=\{11, 5, 4, 3\}$
or
![]() $\{11, 5, 4, 3, 2\}$
. Arguing similarly as (5.5), we get
$\{11, 5, 4, 3, 2\}$
. Arguing similarly as (5.5), we get
![]() $-K_X^3>1$
or
$-K_X^3>1$
or
![]() $-K_X^3>1.5$
when
$-K_X^3>1.5$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {167}{660}$
or
$-K_X^3\geq \frac {167}{660}$
or
![]() $-K_X^3\geq \frac {233}{660}$
unless
$-K_X^3\geq \frac {233}{660}$
unless
![]() $B_X=\{(1, 2), (2, 5), (1, 3), (1, 4), (1, 11)\}$
with
$B_X=\{(1, 2), (2, 5), (1, 3), (1, 4), (1, 11)\}$
with
![]() $-K_X^3=\frac {17}{660}$
.
$-K_X^3=\frac {17}{660}$
.
To summarize, we conclude the claim that
![]() $-K_X^3\geq \frac {74}{462}$
or
$-K_X^3\geq \frac {74}{462}$
or
![]() $B_X=\{(1, 2), (2$
,
$B_X=\{(1, 2), (2$
,
![]() $5), (1, 3), (1$
,
$5), (1, 3), (1$
,
![]() $4), (1, 11)\}$
with
$4), (1, 11)\}$
with
![]() $-K_X^3=\frac {17}{660}$
.
$-K_X^3=\frac {17}{660}$
.
If
![]() $-K_X^3\geq \frac {74}{462}$
, then by Proposition 4.8(2) (with
$-K_X^3\geq \frac {74}{462}$
, then by Proposition 4.8(2) (with
![]() $t=5.7$
), we can take
$t=5.7$
), we can take
![]() $m_1=21$
. Then, by Theorem 3.4(3),
$m_1=21$
. Then, by Theorem 3.4(3),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 51$
.
$m\geq 51$
.
Now, we consider the case
![]() $B_X=\{(1, 2), (2, 5), (1, 3), (1, 4), (1, 11)\}$
with
$B_X=\{(1, 2), (2, 5), (1, 3), (1, 4), (1, 11)\}$
with
![]() $-K_X^3=\frac {17}{660}$
. By Corollary 4.9 (with
$-K_X^3=\frac {17}{660}$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=4.8$
),
$t=4.8$
),
![]() $P_{-18}-1>18$
. If
$P_{-18}-1>18$
. If
![]() $|-18K_X|$
and
$|-18K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {18}{P_{-18}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
$\mu _0'=\frac {18}{P_{-18}-1}<1$
by Remark 3.2. By Proposition 4.8(2) (with
![]() $t=14.4$
), we can take
$t=14.4$
), we can take
![]() $m_1=53$
. By Lemma 3.3,
$m_1=53$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {660}{11m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
$N_0\geq \lceil \frac {660}{11m_{1}}\rceil =2$
. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 52$
. If
$m\geq 52$
. If
![]() $|-18K_X|$
and
$|-18K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=18$
and
$m_1=18$
and
![]() $\mu _0'=m_0=8$
. By Lemma 3.3,
$\mu _0'=m_0=8$
. By Lemma 3.3,
![]() $N_0\geq \lceil \frac {660}{11m_{1}}\rceil =4$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {660}{11m_{1}}\rceil =4$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 45$
.
$m\geq 45$
.
Case 5.
![]() $r_{\max }=12$
.
$r_{\max }=12$
.
If
![]() $r_{\max }=12$
, then we claim that
$r_{\max }=12$
, then we claim that
![]() $r_X\leq 132$
or
$r_X\leq 132$
or
![]() $r_X=420$
.
$r_X=420$
.
By (2.4), at most one element of
![]() $\{6, 7, 8, 9, 10, 11\}$
is in
$\{6, 7, 8, 9, 10, 11\}$
is in
![]() $\mathcal {R}_X$
. So
$\mathcal {R}_X$
. So
![]() $r_X$
divides one element of
$r_X$
divides one element of
![]() $\{120, 180, 420, 660\}$
. Recalling that
$\{120, 180, 420, 660\}$
. Recalling that
![]() $12$
divides
$12$
divides
![]() $r_X$
, it is clear that
$r_X$
, it is clear that
![]() $r_X\leq 132$
or
$r_X\leq 132$
or
![]() $r_X\in \{180, 420, 660\}$
. Moreover, if
$r_X\in \{180, 420, 660\}$
. Moreover, if
![]() $r_X\in \{180, 660\}$
, then
$r_X\in \{180, 660\}$
, then
![]() $\{12, 9, 5\}\subset \mathcal {R}_X$
or
$\{12, 9, 5\}\subset \mathcal {R}_X$
or
![]() $\{12, 11, 5\}\subset \mathcal {R}_X$
, which contradicts (2.4). This concludes the claim.
$\{12, 11, 5\}\subset \mathcal {R}_X$
, which contradicts (2.4). This concludes the claim.
If
![]() $r_X\leq 132$
, then by Corollary 3.7(2),
$r_X\leq 132$
, then by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 43$
.
$m\geq 43$
.
If
![]() $r_X=420$
, then by (2.4),
$r_X=420$
, then by (2.4),
![]() $\mathcal {R}_X=\{12, 7, 5\}$
. Arguing similarly as (5.3), we get
$\mathcal {R}_X=\{12, 7, 5\}$
. Arguing similarly as (5.3), we get
![]() $-K_X^3\geq \frac {241}{420}$
when
$-K_X^3\geq \frac {241}{420}$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.4), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.4), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {241}{420}$
. By Proposition 4.8(2) (with
$-K_X^3\geq \frac {241}{420}$
. By Proposition 4.8(2) (with
![]() $t=2.75$
), we can take
$t=2.75$
), we can take
![]() $m_1=11$
. Hence, by Lemma 3.3,
$m_1=11$
. Hence, by Lemma 3.3,
![]() $N_0\geq \lceil \frac {420}{12m_{1}}\rceil =4$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {420}{12m_{1}}\rceil =4$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 40$
.
$m\geq 40$
.
Case 6.
![]() $r_{\max }=13$
.
$r_{\max }=13$
.
If
![]() $r_{\max }=13$
, then we claim that
$r_{\max }=13$
, then we claim that
![]() $r_X\leq 364$
or
$r_X\leq 364$
or
![]() $r_X=390$
or
$r_X=390$
or
![]() $r_X=546$
.
$r_X=546$
.
By (2.4), at most one element of
![]() $\{6, 7, 8, 9, 10, 11, 12\}$
is in
$\{6, 7, 8, 9, 10, 11, 12\}$
is in
![]() $\mathcal {R}_X$
. So
$\mathcal {R}_X$
. So
![]() $r_X$
divides one element of
$r_X$
divides one element of
![]() $\{5,460, 1,560, 2,340, 8,580\}$
. Recalling that
$\{5,460, 1,560, 2,340, 8,580\}$
. Recalling that
![]() $13$
divides
$13$
divides
![]() $r_X$
and
$r_X$
and
![]() $r_X\leq 660$
, it is clear that
$r_X\leq 660$
, it is clear that
![]() $r_X\leq 364$
or
$r_X\leq 364$
or
![]() $r_X\in \{390, 429, 455, 468$
,
$r_X\in \{390, 429, 455, 468$
,
![]() $520, 546, 572$
,
$520, 546, 572$
,
![]() $585\}$
. Moreover, if
$585\}$
. Moreover, if
![]() $r_X\in \{429, 455, 468$
,
$r_X\in \{429, 455, 468$
,
![]() $520, 572, 585\}$
, then we can see that
$520, 572, 585\}$
, then we can see that
![]() $\mathcal {R}_X$
violates (2.4) by discussing the factors. For example, if
$\mathcal {R}_X$
violates (2.4) by discussing the factors. For example, if
![]() $r_X=455$
, then
$r_X=455$
, then
![]() $\{13, 7, 5\}\subset \mathcal {R}_X$
which violates (2.4). This concludes the claim.
$\{13, 7, 5\}\subset \mathcal {R}_X$
which violates (2.4). This concludes the claim.
If
![]() $P_{-4}=1$
, then
$P_{-4}=1$
, then
![]() $P_{-k}=1$
for
$P_{-k}=1$
for
![]() $1\leq k\leq 4$
. By [Reference Chen and Chen2, Subsubcase II-4f of Proof of Th. 4.4],
$1\leq k\leq 4$
. By [Reference Chen and Chen2, Subsubcase II-4f of Proof of Th. 4.4],
![]() $B_X$
is dominated by
$B_X$
is dominated by
for some
![]() $s_2\geq s_1\geq 4$
. As
$s_2\geq s_1\geq 4$
. As
![]() $r_{\max }=13$
,
$r_{\max }=13$
,
![]() $(s_1, s_2)=(6, 7)$
. Considering all possible packings, we get the following possibilities of
$(s_1, s_2)=(6, 7)$
. Considering all possible packings, we get the following possibilities of
![]() $B_X$
:
$B_X$
:
 $$ \begin{align*} {}& \{2\times (1, 2), 2\times (1, 3), (2, 13)\},\\ {}& \{(1, 2), (2, 5), (1, 3), (2, 13)\},\\ {}& \{(3, 7), (1, 3), (2, 13)\},\\ {}& \{(1, 2), (3, 8), (2, 13)\},\\ {}& \{2\times(2, 5), (2, 13)\}. \end{align*} $$
$$ \begin{align*} {}& \{2\times (1, 2), 2\times (1, 3), (2, 13)\},\\ {}& \{(1, 2), (2, 5), (1, 3), (2, 13)\},\\ {}& \{(3, 7), (1, 3), (2, 13)\},\\ {}& \{(1, 2), (3, 8), (2, 13)\},\\ {}& \{2\times(2, 5), (2, 13)\}. \end{align*} $$
Then
![]() $r_X\leq 273$
or
$r_X\leq 273$
or
![]() $B_X=\{(1, 2), (2, 5), (1, 3), (2, 13)\}$
.
$B_X=\{(1, 2), (2, 5), (1, 3), (2, 13)\}$
.
If
![]() $r_X\leq 273$
, then by Corollary 3.7(2),
$r_X\leq 273$
, then by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 55$
.
$m\geq 55$
.
If
![]() $B_X=\{(1, 2), (2, 5), (1, 3), (2, 13)\}$
, then
$B_X=\{(1, 2), (2, 5), (1, 3), (2, 13)\}$
, then
![]() $-K_X^3=\frac {23}{390}$
. By Corollary 4.9 (with
$-K_X^3=\frac {23}{390}$
. By Corollary 4.9 (with
![]() $l=1$
and
$l=1$
and
![]() $t=3$
),
$t=3$
),
![]() $P_{-13}-1>13$
. If
$P_{-13}-1>13$
. If
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-8K_X|$
are composed with the same pencil, then take
$|-8K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
. If
$m\geq 56$
. If
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-8K_X|$
are not composed with the same pencil, then take
$|-8K_X|$
are not composed with the same pencil, then take
![]() $m_1=13$
and
$m_1=13$
and
![]() $\mu _0'=m_0=8$
. Then, by Lemma 3.3,
$\mu _0'=m_0=8$
. Then, by Lemma 3.3,
![]() $N_0\geq \lceil \frac {390}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {390}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 44$
.
$m\geq 44$
.
So, from now on, we assume that
![]() $P_{-4}\geq 2$
and take
$P_{-4}\geq 2$
and take
![]() $m_0=4$
. We take
$m_0=4$
. We take
![]() $\mu _0'=4$
unless stated otherwise.
$\mu _0'=4$
unless stated otherwise.
If
![]() $r_X\leq 364$
, then by Corollary 3.7(1),
$r_X\leq 364$
, then by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 57$
.
$m\geq 57$
.
If
![]() $r_X=546$
, then by (2.4),
$r_X=546$
, then by (2.4),
![]() $\mathcal {R}_X=\{13, 7, 3, 2\}$
. Arguing similarly as (5.5), we get
$\mathcal {R}_X=\{13, 7, 3, 2\}$
. Arguing similarly as (5.5), we get
![]() $-K_X^3>0.9$
when
$-K_X^3>0.9$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {157}{546}$
. By Proposition 4.8(2) (with
$-K_X^3\geq \frac {157}{546}$
. By Proposition 4.8(2) (with
![]() $t=3.6$
), we can take
$t=3.6$
), we can take
![]() $m_1=16$
. Hence, by Lemma 3.3,
$m_1=16$
. Hence, by Lemma 3.3,
![]() $N_0\geq \lceil \frac {546}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {546}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 44$
.
$m\geq 44$
.
If
![]() $r_X=390$
, then by (2.4),
$r_X=390$
, then by (2.4),
![]() $\mathcal {R}_X=\{13, 6, 5\}$
or
$\mathcal {R}_X=\{13, 6, 5\}$
or
![]() $\{13, 5, 3, 2\}$
or
$\{13, 5, 3, 2\}$
or
![]() $\{13, 5, 3, 2, 2\}$
. Arguing similarly as (5.5), we get
$\{13, 5, 3, 2, 2\}$
. Arguing similarly as (5.5), we get
![]() $-K_X^3>0.5$
or
$-K_X^3>0.5$
or
![]() $-K_X^3>0.8$
or
$-K_X^3>0.8$
or
![]() $-K_X^3>1$
when
$-K_X^3>1$
when
![]() $P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
$P_{-1}\geq 2$
. Arguing similarly as (5.6), we get constrains for
![]() $B_X$
when
$B_X$
when
![]() $P_{-1}=1$
. By (2.2) and considering all the possible baskets when
$P_{-1}=1$
. By (2.2) and considering all the possible baskets when
![]() $P_{-1}=1$
, we can see that
$P_{-1}=1$
, we can see that
![]() $-K_X^3\geq \frac {133}{390}$
or
$-K_X^3\geq \frac {133}{390}$
or
![]() $-K_X^3\geq \frac {23}{390}$
or
$-K_X^3\geq \frac {23}{390}$
or
![]() $-K_X^3\geq \frac {62}{390}$
. By Corollary 4.9 (with
$-K_X^3\geq \frac {62}{390}$
. By Corollary 4.9 (with
![]() $l=1, t=3$
, and
$l=1, t=3$
, and
![]() $-K_X^3\geq \frac {23}{390}$
),
$-K_X^3\geq \frac {23}{390}$
),
![]() $P_{-13}-1>13$
. If
$P_{-13}-1>13$
. If
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-4K_X|$
are composed with the same pencil, then take
$|-4K_X|$
are composed with the same pencil, then take
![]() $\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
$\mu _0'=\frac {13}{P_{-13}-1}<1$
by Remark 3.2. Then, by Corollary 3.7(1),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 56$
. If
$m\geq 56$
. If
![]() $|-13K_X|$
and
$|-13K_X|$
and
![]() $|-4K_X|$
are not composed with the same pencil, then take
$|-4K_X|$
are not composed with the same pencil, then take
![]() $m_1=13$
and
$m_1=13$
and
![]() $\mu _0'=m_0=4$
. Then, by Lemma 3.3,
$\mu _0'=m_0=4$
. Then, by Lemma 3.3,
![]() $N_0\geq \lceil \frac {390}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
$N_0\geq \lceil \frac {390}{13m_{1}}\rceil =3$
. Then, by Corollary 3.7(2),
![]() $\varphi _{-m}$
is birational for all
$\varphi _{-m}$
is birational for all
![]() $m\geq 40$
.
$m\geq 40$
.
Combining all above cases, we have proved the theorem.
5.5 Proofs of Theorem 1.2 and Theorem 1.4
Proof of Theorem 1.4
From the proof of Theorem 1.2,
![]() $\varphi _{-58}$
may not be birational only if
$\varphi _{-58}$
may not be birational only if
![]() $B_X=\{(1, 2), 2\times (1, 3), (8, 17)\}$
,
$B_X=\{(1, 2), 2\times (1, 3), (8, 17)\}$
,
![]() $P_{-1}=0$
, and
$P_{-1}=0$
, and
![]() $|-24K_X|$
is composed with a pencil. In this case,
$|-24K_X|$
is composed with a pencil. In this case,
![]() $r_X(-K_X^3)=7$
and
$r_X(-K_X^3)=7$
and
![]() $P_{-24}=169=7\times 24+1$
by (2.1). But this contradicts Proposition 4.11.
$P_{-24}=169=7\times 24+1$
by (2.1). But this contradicts Proposition 4.11.
Appendix
The possible baskets with
![]() $P_{-2}=0$
are the following (cf. [Reference Chen and Chen2, Th. 3.5]).
$P_{-2}=0$
are the following (cf. [Reference Chen and Chen2, Th. 3.5]).
Table A.1 Baskets with
![]() $P_{-2}=0$
.
$P_{-2}=0$
.

The possible baskets with
![]() $P_{-1}=0$
and
$P_{-1}=0$
and
![]() $P_{-2}=P_{-4}=1$
are the following (cf. the second paragraph of [Reference Chen and Jiang5, Case IV of Proof of Th. 1.8]).
$P_{-2}=P_{-4}=1$
are the following (cf. the second paragraph of [Reference Chen and Jiang5, Case IV of Proof of Th. 1.8]).
Table A.2 Baskets with
![]() $P_{-1}=0$
and
$P_{-1}=0$
and
![]() $P_{-2}=P_{-4}=1$
.
$P_{-2}=P_{-4}=1$
.

Acknowledgments
Zou would like to thank her advisor, Professor Meng Chen, for his support and encouragement. We are grateful to Meng Chen for discussions and suggestions. Jiang is a member of LMNS, Fudan University. We would like to thank the referee for useful suggestions.