Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-04T09:36:41.060Z Has data issue: false hasContentIssue false
  • English
  • Français

On some degenerate parabolic equations II

Published online by Cambridge University Press:  22 January 2016

Tadato Matsuzawa
Tadato Matsuzawa*
Affiliation:
Department of Mathematics, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the article I: [8], we have proved the hypoellipticity of a degenerate parabolic equation of the form:

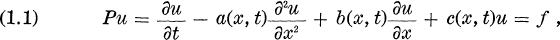
where the coefficients a(x, t), b(x,t) and c(x, t) are complex valued smooth functions. The fundamental assumption on the coefficients is that Re a(x, t) satisfies the condition of Nirenberg and Treves ([8], (1.5)). To prove the hypoellipticity we have constructed recurcively the parametrices as pseudodifferential operators with parameter. This method may be viewed as an improvement of that of [9] and [7]. We have analyzed the properties of these parametrices by estimating the symbols with parameter associated with the given operator. We shall summerize these results in §3.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 52 , December 1973 , pp. 61 - 84
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Bodanko, W.: Sur le problème de Cauchy et les problèmes de Fourier pour les équations paraboliques dans un domaine non borné, Ann. Polon. Math., 18 (1966), 79–94.CrossRefGoogle Scholar
[2] Friedman, A.: Partial differential equations of parabolic type, Prentice-Hall (1964).Google Scholar
[3] Hormander, L.: Pseudo-differential operators and hypoelliptic equations, Amer. Math. Soc. Symp. Pure Math. 10 (1966), Singular integral operators, 138–183.Google Scholar
[4] Hormander, L.: Fourier integral operators, I, Acta Math., 127 (1971), 79–783.CrossRefGoogle Scholar
[5] Hormander, L.: Hypoelliptic second order differential equations, Acta Math., 119 (1968), 147–171.CrossRefGoogle Scholar
[6] Igari, K.: Degenerate parabolic differential equations, to appear.Google Scholar
[7] Kato, Y.: The hypoellipticity of degenerate parabolic differential operators, J. Functional Analysis, Vol. 7, No. 1 (1971), 116–131.CrossRefGoogle Scholar
[8] Matsuzawa, T.: On some degenerate parabolic equations I, Nagoya Math. J. Vol. 51 (1973), 57–77.CrossRefGoogle Scholar
[9] Mizohata, S.: Hypoellipticité des équations paraboliques, Bull. Soc. Math. France, 85 (1957), 15–50.CrossRefGoogle Scholar
[10] Nirenberg, L. and Treves, F.: On local solvability of linear partial differential equations, Part I: Necessary conditions. Comm. Pure Appl. Math., Vol. 23 (1970), 1–38.CrossRefGoogle Scholar
[11] Oleinik, O. A.: On the smoothness of the solutions of degenerate elliptic and parabolic equations, Sov. Math. Dokl., 6 (1965), 972–976.Google Scholar
[12] Oleinik, O. A.: Linear equations of second order with non-negative form, Math. USSR-Sb., 69 (1966), 111–140 (in Russian). Amer. Math. Soc. Translation, 167–199.Google Scholar
[13] Treves, F.: A new method of proof of the subelliptic estimates, Comm. Pure Appl. Math., Vol. 24 (1971), 71–115.CrossRefGoogle Scholar
[14] Treves, F.: Analytic-hypoelliptic partial differential equations of principal type, Comm. Pure Appl. Math., 24 (1971), 537–570.CrossRefGoogle Scholar
[15] Schwartz, L.: Théorie des distributions, Vol. 1, Hermann, Paris (1957).Google Scholar