Article contents
On some class number relations for Galois extensions
Published online by Cambridge University Press: 22 January 2016
Extract
Let k be an algebraic number field of finite degree over Q, the field of rationals, and K be an extension of finite degree over k. By the use of the class number of algebraic tori, we can introduce an arithmetical invariant E(K/k) for the extension K/k. When k = Q and K is quadratic over Q, the formula of Gauss on the genera of binary quadratic forms, i.e. the formula 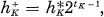 where
where 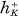 = the class number of K in the narrow sense,
= the class number of K in the narrow sense, 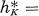 the number of classes is a genus of the norm form of K/Q and tK = the number of distinct prime factors of the discriminant
the number of classes is a genus of the norm form of K/Q and tK = the number of distinct prime factors of the discriminant 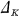 of K, may be considered as an equality between E(K/Q) and other arithmetical invariants of K.
of K, may be considered as an equality between E(K/Q) and other arithmetical invariants of K.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1987
References
- 8
- Cited by


