Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bredikhin, B. M.
1980.
Partition into terms with prime numbers.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
869.
Timofeev, N. M.
and
Khripunova, M. B.
1996.
The Titchmarsh problem with integers having a given number of prime divisors.
Mathematical Notes,
Vol. 59,
Issue. 4,
p.
421.
Тимофеев, Николай Михайлович
Timofeev, Nikolai Michailovich
Хрипунова, Марина Борисовна
and
Khripunova, Marina Borisovna
1996.
Проблема Титчмарша с числами, имеющими заданное число простых делителей.
Математические заметки,
Vol. 59,
Issue. 4,
p.
586.
Khripunova, M. B.
1998.
Additive problems for integers with a given number of prime divisors.
Mathematical Notes,
Vol. 63,
Issue. 5,
p.
658.
Хрипунова, Марина Борисовна
and
Khripunova, Marina Borisovna
1998.
Аддитивные задачи с числами, имеющими заданное число простых делителей.
Математические заметки,
Vol. 63,
Issue. 5,
p.
749.
Darbar, P.
and
Mukhopadhyay, A.
2021.
A Bombieri-type theorem for convolution with application on number field.
Acta Mathematica Hungarica,
Vol. 163,
Issue. 1,
p.
37.


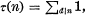 then the above problem is to get an asymptotic law for the sum
then the above problem is to get an asymptotic law for the sum
