Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-03T08:50:59.312Z Has data issue: false hasContentIssue false
  • English
  • Français

On Multiple Transitivity of Permutation Groups

Published online by Cambridge University Press:  22 January 2016

Tosiro Tsuzuku
Tosiro Tsuzuku*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

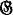It is well known that a doubly transitive group has an irreducible character χ1 such that χ1(R) = α(R) − 1 for any element R of 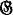and a quadruply transitive group has irreducible characters χ3 and χ3 such that χ2(R) = 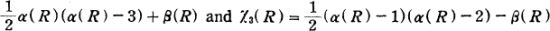where α(R) and β(R) are respectively the numbers of one cycles and two cycles contained in R. G. Frobenius was led to this fact in the connection with characters of the symmetric groups and he proved the following interesting theorem: if a permutation group 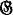of degree n is t-ply transitive, then any irreducible character of the symmetric group of degree n with dimension at most equal to 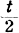is an irreducible character of .

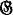Type
Research Article
Information
Nagoya Mathematical Journal , Volume 18 , April 1961 , pp. 93 - 109
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1961

References

[1] Dickson, L. E., Linear Groups, Leipzig (Teubner) 1901.Google Scholar
[2] Frobenius, G., Über die Charaktere der symmetrischen Gruppe, Sitzungsber. Preuss. Akad. (1900), pp. 516–534.Google Scholar
[3] Frobenius, G., Über die Charaktere der alternierenden Gruppe, Sitzungsber. Preuss. Akad. (1901), pp. 303–315.Google Scholar
[4] Frobenius, G., Über die Charaktere der mehrfach transitiven Gruppe, Sitzungsber. Preuss. Akad. (1904), pp. 558–571.Google Scholar
[5] Littlewood, D. E., The Theory of Group Characters, Oxford 1940.Google Scholar
[6] Weyl, H., The Classical Groups, Princeton 1938.Google Scholar
[7] Witt, E., Die 5·fach transitiven Gruppen von Mathieu, Abh. Math. Sem. Univ. Hamburg, Bd. 12 (1938), pp. 256–264.Google Scholar