Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koike, Masao
1985.
Mathieu group M24 and modular forms.
Nagoya Mathematical Journal,
Vol. 99,
Issue. ,
p.
147.
KOIKE, Masao
1986.
Moonshines of <i>PSL</i><sub>2</sub>(<i>F<sub>q</sub></i>) and the automorphism group of Leech lattice.
Japanese journal of mathematics. New series,
Vol. 12,
Issue. 2,
p.
283.
Beukers, F.
1987.
Another congruence for the Apéry numbers.
Journal of Number Theory,
Vol. 25,
Issue. 2,
p.
201.
Koike, Masao
1988.
Modular forms and the automorphism group of Leech lattice.
Nagoya Mathematical Journal,
Vol. 112,
Issue. ,
p.
63.
Mason, Geoffrey
1990.
On a system of elliptic modular forms attached to the large Mathieu group.
Nagoya Mathematical Journal,
Vol. 118,
Issue. ,
p.
177.
Dong, Chongying
and
Mason, Geoffrey
1994.
An orbifold theory of genus zero associated to the sporadic groupM 24.
Communications in Mathematical Physics,
Vol. 164,
Issue. 1,
p.
87.
Voskresenskaya, G. V.
1995.
Cusp forms and finite subgroups inSL(5, ?).
Functional Analysis and Its Applications,
Vol. 29,
Issue. 2,
p.
129.
Martin, Yves
1996.
Multiplicative 𝜂-quotients.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 12,
p.
4825.
Воскресенская, Галина Валентиновна
and
Voskresenskaya, Galina Valentinovna
2003.
Мультипликативные произведения эта-функций Дедекинда и представления групп.
Математические заметки,
Vol. 73,
Issue. 4,
p.
511.
ROYER, EMMANUEL
2007.
EVALUATING CONVOLUTION SUMS OF THE DIVISOR FUNCTION BY QUASIMODULAR FORMS.
International Journal of Number Theory,
Vol. 03,
Issue. 02,
p.
231.
Voskresenskaya, G. V.
2007.
On the problem of classification of finite groups associated to multiplicative η-products.
Journal of Mathematical Sciences,
Vol. 140,
Issue. 2,
p.
206.
Voskresenskaya, G. V.
2010.
Finite simple groups and multiplicative η-products.
Journal of Mathematical Sciences,
Vol. 171,
Issue. 3,
p.
344.
Voskresenskaya, G. V.
2012.
Arithmetic properties of shimura sums related to several modular forms.
Journal of Mathematical Sciences,
Vol. 182,
Issue. 4,
p.
444.
Eguchi, Tohru
and
Hikami, Kazuhiro
2012.
Twisted Elliptic Genus for K3 and Borcherds Product.
Letters in Mathematical Physics,
Vol. 102,
Issue. 2,
p.
203.
Voskresenskaya, G. V.
2014.
The Dedekind Eta-Function in Algebra and Number Theory: Old and New Problems.
Journal of Mathematical Sciences,
Vol. 199,
Issue. 3,
p.
248.
Voskresenskaya, G. V.
2018.
Dedekind η-Function in Modern Research.
Journal of Mathematical Sciences,
Vol. 235,
Issue. 6,
p.
788.


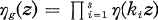 . In this paper, we shall prove McKay’s conjecture which gives some combinatorial conditions about
. In this paper, we shall prove McKay’s conjecture which gives some combinatorial conditions about 