Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-22T05:51:23.604Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MALLE’S CONJECTURE FOR THE PRODUCT OF SYMMETRIC AND NILPOTENT GROUPS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  17 February 2025

HRISHABH MISHRA Open the ORCID record for HRISHABH MISHRA [Opens in a new window]  and
ANWESH RAY Open the ORCID record for ANWESH RAY [Opens in a new window]
HRISHABH MISHRA
Affiliation:
Department of Mathematics Chennai Mathematical Institute H1, SIPCOT IT Park, Kelambakkam Siruseri, Tamil Nadu 603103, India [email protected]
ANWESH RAY*
Affiliation:
Department of Mathematics Chennai Mathematical Institute H1, SIPCOT IT Park, Kelambakkam Siruseri, Tamil Nadu 603103, India
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite nilpotent group and 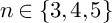$n\in \{3,4, 5\}$. Consider 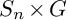$S_n\times G$ as a subgroup of 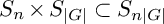$S_n\times S_{|G|}\subset S_{n|G|}$, where G embeds into the second factor of 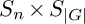$S_n\times S_{|G|}$ via the regular representation. Over any number field k, we prove the strong form of Malle’s conjecture (cf. Malle (2002, Journal of Number Theory 92, 315–329)) for 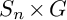$S_n\times G$ viewed as a subgroup of $S_{n|G|}$. Our result requires that G satisfies some mild conditions.

Keywords

Malle’s conjecturenilpotent groupscounting number fields

MSC classification

Primary: 11R21: Other number fields 11R32: Galois theory 11R45: Density theorems
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alberts, B., The weak form of Malle’s conjecture and solvable groups , Res. Number Theory 6 (2020), no. 1, Paper No. 10, 23.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quartic rings and fields , Ann Math. 162 (2005), no. 2, 1031–1063.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quintic rings and fields , Ann. Math. 172 (2010), no. 3, 1559–1591.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X., Geometry-of-numbers methods over global fields I: Prehomogeneous vector spaces, arXiv:1512.03035, 2015.Google Scholar
Cohen, H., Y. Diaz, F. D. and Olivier, M., Enumerating quartic dihedral extensions of , Compos. Math. 133 (2002), no. 1, 65–93.CrossRefGoogle Scholar
Harold Davenport and Hans Arnold Heilbronn, On the density of discriminants of cubic fields. II , Proc. Royal Soc. London. A. Math. Phys. Sci. 322 (1971), no. 1551, 405–420.Google Scholar
Datskovsky, B. and Wright, D. J., Density of discriminants of cubic extensions , J. Reine Angew. Math. 386 (1988), 116–138.Google Scholar
Klüners, J., A counter example to Malle’s conjecture on the asymptotics of discriminants , C. R. Math. 340 (2005), no. 6, 411–414.CrossRefGoogle Scholar
Klüners, J. and Malle, G., Counting nilpotent Galois extensions , J. Reine Angew. Math. 572 (2004), 1–26.CrossRefGoogle Scholar
Koymans, P. and Pagano, C., On Malle’s conjecture for nilpotent groups , Trans. Amer. Math. Soc. Ser. B 10 (2023), 310–354.CrossRefGoogle Scholar
Mäki, S., On the density of abelian number fields, vol. 54, Finnish Mathematical Society, Helsinki, 1985.Google Scholar
Malle, G., On the distribution of Galois groups , J. Number Theory 92 (2002), no. 2, 315–329.CrossRefGoogle Scholar
Malle, G., On the distribution of Galois groups, II , Exp. Math. 13 (2004), no. 2, 129–135.CrossRefGoogle Scholar
Masri, R., Thorne, F., Tsai, W.-L. and Wang, J., Malle’s conjecture for $G\times A$ , with G= ${S}_3$ , ${S}_4$ , ${S}_5$ , 2020, 22 pp.Google Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory, volume 163 of Graduate Studies in Mathematics, third edition, American Mathematical Society, Providence, RI, 2015.CrossRefGoogle Scholar
Wang, J., Malle’s conjecture for ${S}_n\times A$ for $n=3,4,5$ , Compos. Math. 157 (2021), no. 1, 83–121.CrossRefGoogle Scholar
Wright, D. J., Distribution of discriminants of abelian extensions . Proc. London Math. Soc. 3 (1989), no. 1, 17–50.CrossRefGoogle Scholar