Article contents
On Local Maximality for the Coefficient a6
Published online by Cambridge University Press: 22 January 2016
Extract
Recently a number of authors have studied the application of Grunsky’s coefficient inequalities to the study of the Bieberbach conjecture for the class of normalized regular univalent functions f(z) in the unit circle |z|< 1
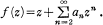
Charzynski and Schiffer [2] applied this result to give an elementary proof of the inequality | a4 | Ȧ 4. One of the present authors [8] proved that if a2 is real non-negative then 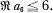 A natural first step in the study of the inequality for a coefficient is to prove local maximality for a2 near to 2.
A natural first step in the study of the inequality for a coefficient is to prove local maximality for a2 near to 2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1966
References
- 6
- Cited by


