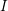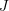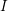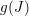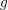ON HILBERT FUNCTIONS OF GENERAL INTERSECTIONS OF IDEALS

Abstract

Let $I$ and $J$ be homogeneous ideals in a standard graded polynomial ring. We study upper bounds of the Hilbert function of the intersection of $I$ and $g(J)$, where $g$ is a general change of coordinates. Our main result gives a generalization of Green’s hyperplane section theorem.

1 Introduction

Hilbert functions of graded $K$-algebras are important invariants studied in several areas of mathematics. In the theory of Hilbert functions, one of the most useful tools is Green’s hyperplane section theorem, which gives a sharp upper bound for the Hilbert function of $R/hR$, where $R$ is a standard graded $K$-algebra and $h$ is a general linear form, in terms of the Hilbert function of $R$. This result of Green has been extended to the case of general homogeneous polynomials by Herzog and Popescu [HP] and Gasharov [Ga]. In this paper, we study a further generalization of these theorems.

Let $K$ be an infinite field and $S=K[x_{1},\ldots ,x_{n}]$ a standard graded polynomial ring. Recall that the Hilbert function $H(M):\mathbb{Z}\rightarrow \mathbb{Z}$ of a finitely generated graded $S$-module $M$ is the numerical function defined by

$$\begin{eqnarray}H(M)(d)=\dim _{K}M_{d},\end{eqnarray}$$

where $M_{d}$ is the graded component of $M$ of degree $d$. A set $W$ of monomials of $S$ is said to be a lex-segment if, for all monomials $u,v\in S$ of the same degree, $u\in W$ and $v{>}_{\text{lex}}u$ imply $v\in W$, where ${>}_{\text{lex}}$ is the lexicographic order induced by the ordering $x_{1}>\cdots >x_{n}$. We say that a monomial ideal $I\subset S$ is a lex-segment ideal if the set of monomials in $I$ is a lex-segment. The classical Macaulay’s theorem [Mac] guarantees that, for any homogeneous ideal $I\subset S$, there exists a unique lex-segment ideal, denoted by $I^{\text{lex}}$, with the same Hilbert function as $I$. Green’s hyperplane section theorem [Gr] states

Theorem 1.1. (Green’s hyperplane section theorem)

Let $I\subset S$ be a homogeneous ideal. For a general linear form $h\in S_{1}$,

$$\begin{eqnarray}H(I\cap (h))(d)\leqslant H(I^{\text{lex}}\cap (x_{n}))(d)\quad \text{for all }d\geqslant 0.\end{eqnarray}$$

Green’s hyperplane section theorem is known to be useful to prove several important results on Hilbert functions such as Macaulay’s theorem [Mac] and Gotzmann’s persistence theorem [Go] (see [Gr]). Herzog and Popescu [HP] (in characteristic $0$) and Gasharov [Ga] (in positive characteristic) generalized Green’s hyperplane section theorem in the following form.

Theorem 1.2. (Herzog–Popescu, Gasharov)

Let $I\subset S$ be a homogeneous ideal. For a general homogeneous polynomial $h\in S$ of degree $a$,

$$\begin{eqnarray}H(I\cap (h))(d)\leqslant H(I^{\text{lex}}\cap (x_{n}^{a}))(d)\quad \text{for all }d\geqslant 0.\end{eqnarray}$$

We study a generalization of Theorems 1.1 and 1.2. Let ${>}_{\text{oplex}}$ be the lexicographic order on $S$ induced by the ordering $x_{n}>\cdots >x_{1}$. A set $W$ of monomials of $S$ is said to be an opposite lex-segment if, for all monomials $u,v\in S$ of the same degree, $u\in W$ and $v{>}_{\text{oplex}}u$ imply $v\in W$. Also, we say that a monomial ideal $I\subset S$ is an opposite lex-segment ideal if the set of monomials in $I$ is an opposite lex-segment. For a homogeneous ideal $I\subset S$, let $I^{\text{oplex}}$ be the opposite lex-segment ideal with the same Hilbert function as $I$ and let $\text{Gin}_{{\it\sigma}}(I)$ be the generic initial ideal [Ei, Section 15.9] of $I$ with respect to a term order ${>}_{{\it\sigma}}$.

In Section 3 we prove the following

Theorem 1.3. Suppose $\text{char}(K)=0$. Let $I\subset S$ and $J\subset S$ be homogeneous ideals such that $\text{Gin}_{\text{lex}}(J)$ is a lex-segment ideal. For a general change of coordinates $g$ of $S$,

$$\begin{eqnarray}H(I\cap g(J))(d)\leqslant H(I^{\text{lex}}\cap J^{\text{oplex}})(d)\quad \text{for all }d\geqslant 0.\end{eqnarray}$$

Theorems 1.1 and 1.2, assuming that the characteristic is zero, are special cases of the above theorem when $J$ is principal. Note that Theorem 1.3 is sharp since the equality holds if $I$ is a lex-segment ideal and $J$ is an opposite lex-segment ideal (Remark 3.5). Note also that if $\text{Gin}_{{\it\sigma}}(I)$ is a lex-segment ideal for some term order ${>}_{{\it\sigma}}$ then $\text{Gin}_{\text{lex}}(J)$ must be a lex-segment ideal as well [Co1, Corollary 1.6].

Unfortunately, the assumption on $J$, as well as the assumption on the characteristic of $K$, in Theorem 1.3 are essential (see Remark 3.6). However, we prove the following result for the product of ideals.

Theorem 1.4. Suppose $\text{char}(K)=0$. Let $I\subset S$ and $J\subset S$ be homogeneous ideals. For a general change of coordinates $g$ of $S$,

$$\begin{eqnarray}H(Ig(J))(d)\geqslant H(I^{\text{lex}}J^{\text{oplex}})(d)\quad \text{for all }d\geqslant 0.\end{eqnarray}$$

Inspired by Theorems 1.3 and 1.4, we suggest the following conjecture.

Conjecture 1.5. Suppose $\text{char}(K)=0.$ Let $I\subset S$ and $J\subset S$ be homogeneous ideals such that $\text{Gin}_{\text{lex}}(J)$ is a lex-segment ideal. For a general change of coordinates $g$ of $S$,

$$\begin{eqnarray}H(\text{Tor}_{i}(S/I,S/g(J)))(d)\leqslant H(\text{Tor}_{i}(S/I^{\text{lex}},S/J^{\text{oplex}}))(d)\quad \text{for all }d\geqslant 0.\end{eqnarray}$$

Theorems 1.3 and 1.4 show that the conjecture is true if $i=0$ or $i=1.$ The conjecture is also known to be true when $J$ is generated by linear forms by a result of Conca [Co2, Theorem 4.2]. Theorem 2.7, which we prove later, also provides some evidence supporting the above inequality.

2 Dimension of $\text{Tor}$ and general change of coordinates

Let $\text{GL}_{n}(K)$ be the general linear group of invertible $n\times n$ matrixes over $K$. Throughout the paper, we identify each element $g=(g_{ij})\in \text{GL}_{n}(K)$ with the change of coordinates defined by $g(x_{j})=\sum _{i=1}^{n}g_{ij}x_{i}$ for all $j$.

We say that a property (P) holds for a general $g\in \text{GL}_{n}(K)$ if there is a nonempty Zariski open subset $U\subset \text{GL}_{n}(K)$ such that (P) holds for all $g\in U$.

We first present two lemmas which will allow us to reduce the proofs of the theorems in the introduction to combinatorial considerations regarding Borel-fixed ideals. The first lemma (Lemma 2.1) is probably clearly true to some experts, but we include its proof for the sake of the exposition. The ideas used in the second lemma (Lemma 2.3) are similar to that of [Ca1, Lemma 2.1] and they rely on the construction of a flat family and on the use of the structure theorem for finitely generated modules over principal ideal domains.

For two ideals $I\subset S$ and $J\subset S$, we define the functions $H(\cap ,I,J):\mathbb{Z}\rightarrow \mathbb{Z}$, $H(\cdot ,I,J):\mathbb{Z}\rightarrow \mathbb{Z}$ and $H(+,I,J):\mathbb{Z}\rightarrow \mathbb{Z}$ by

$$\begin{eqnarray}\displaystyle & H(\cap ,I,J)(d)=\min \{H(I\cap g(J))(d):g\in \text{GL}_{n}(K)\}, & \displaystyle \nonumber\\ \displaystyle & H(\cdot ,I,J)(d)=\max \{H(Ig(J))(d):g\in \text{GL}_{n}(K)\} & \displaystyle \nonumber\end{eqnarray}$$

and

$$\begin{eqnarray}H(+,I,J)(d)=\max \{H(I+g(J))(d):g\in \text{GL}_{n}(K)\}\end{eqnarray}$$

for all $d\in \mathbb{Z}$.

Lemma 2.1. Let $I\subset S$ and $J\subset S$ be homogeneous ideals. There is a nonempty Zariski open subset $U\subset \text{GL}_{n}(K)$ such that $H(\cap ,I,J)=H(I\cap g(J))$, $H(\cdot ,I,J)=H(Ig(J))$ and $H(+,I,J)=H(I+g(J))$ for any $g\in U$.

Proof. We prove the statement for $I+g(J)$, which implies the desired statement for $I\cap g(J)$ (the proof for $Ig(J)$ is similar).

Let $t_{kl}$, where $1\leqslant k,l\leqslant n$, be indeterminates, $\tilde{K}=K(t_{kl}:1\leqslant k,l\leqslant n)$ the field of fractions of $K[t_{kl}:1\leqslant k,l\leqslant n]$ and $A=\tilde{K}[x_{1},\ldots ,x_{n}]$. Let ${\it\rho}:S\rightarrow A$ be the ring map induced by ${\it\rho}(x_{l})=\sum _{k=1}^{n}t_{kl}x_{k}$ for $l=1,2,\ldots ,n$, and $\tilde{L}=IA+{\it\rho}(J)A\subset A$. Let $L\subset S$ be the monomial ideal with the same monomial generators as $\text{in}_{\text{lex}}(\tilde{L})$.

We claim that

(1)$$\begin{eqnarray}\displaystyle \dim _{K}L_{d}=\dim _{\tilde{K}}\tilde{L}_{d}\geqslant \dim _{K}(I+g(J))_{d} & & \displaystyle\end{eqnarray}$$

for any $d\in \mathbb{Z}$ and $g\in \text{GL}_{n}(K)$. The first equality is clear. To see the second inequality, let ${\it\alpha}_{1},\ldots ,{\it\alpha}_{\ell }$ be a $K$-basis of $I_{d}$ and let ${\it\beta}_{1},\ldots ,{\it\beta}_{m}$ be that of $J_{d}$. Then $\dim _{K}(I+g(J))_{d}$ is the rank of the matrix representing $({\it\alpha}_{1},\ldots ,{\it\alpha}_{\ell },g({\it\beta}_{1}),\ldots ,g({\it\beta}_{m}))$ with respect to the monomial basis of $S_{d}$. This rank is maximized when $g$ is sufficiently general. Also, this rank equals to $\dim _{\tilde{K}}\tilde{L}_{d}$ for a general $g$.

Let $f_{1},\ldots ,f_{s}$ be generators of $I$ and $g_{1},\ldots ,g_{t}$ those of $J$. Then the polynomials $f_{1},\ldots ,f_{s},{\it\rho}(g_{1}),\ldots ,{\it\rho}(g_{t})$ are generators of $\tilde{L}$. By the Buchberger algorithm, one can compute a Gröbner basis of $\tilde{L}$ from $f_{1},\ldots ,f_{s},{\it\rho}(g_{1}),\ldots ,{\it\rho}(g_{t})$ by finite steps. Consider all elements $h_{1},\ldots ,h_{m}\in K(t_{kl}:1\leqslant k,l\leqslant n)$ which are the coefficients of polynomials (including numerators and denominators of rational functions) that appear in the process of computing a Gröbner basis of $\tilde{L}$ by the Buchberger algorithm. Let $U=\{g\in \text{GL}_{n}(K):h_{i}(g)\neq 0\text{ for }i=1,2,\ldots ,m\}$, where $h_{i}(g)$ is an element obtained from $h_{i}$ by substituting $t_{kl}$ with the entries of $g$. By construction $U$ is a nonempty Zariski open subset and $\text{in}_{\text{lex}}(I+g(J))=L$ for every $g\in U$. This fact and (1) prove the desired statement.◻

The method used to prove the above lemma can be easily generalized to a number of situations. For a finitely generated graded $S$-module $M$ and for a homogeneous ideal $J\subset S$, define the function $H(\text{Tor}_{i},M,J):\mathbb{Z}\rightarrow \mathbb{Z}$ by

$$\begin{eqnarray}H(\text{Tor}_{i},M,J)(d)=\min \{H(\text{Tor}_{i}(M,S/g(J)))(d):g\in \text{GL}_{n}(K)\}\end{eqnarray}$$

for all $d\in \mathbb{Z}$.

Proposition 2.2. With the same notation as above, there is a nonempty Zariski open subset $U\subset \text{GL}_{n}(K)$ such that $H(\text{Tor}_{i},M,J)=H(\text{Tor}_{i}(M,S/g(J)))$ for any $g\in U$.

Proof. Let $\mathbb{F}:0\stackrel{{\it\varphi}_{p+1}}{\longrightarrow }\mathbb{F}_{p}\stackrel{{\it\varphi}_{p}}{\longrightarrow }\cdots \longrightarrow \mathbb{F}_{1}\stackrel{{\it\varphi}_{1}}{\longrightarrow }\mathbb{F}_{0}\stackrel{{\it\varphi}_{0}}{\longrightarrow }0$ be a graded free resolution of $M.$ Given a change of coordinates $g$, one first notes that for every $i=0,1,\ldots ,p$, the Hilbert function $H(\text{Tor}_{i}(M,S/g(J)))$ is equal to the difference between the Hilbert function of $\text{Ker}({\it\pi}_{i-1}\circ {\it\varphi}_{i})$ and that of ${\it\varphi}_{i+1}(F_{i+1})+F_{i}\otimes _{S}g(J)$ where ${\it\pi}_{i-1}:F_{i-1}\rightarrow F_{i-1}\otimes _{S}S/g(J)$ is the canonical projection. Hence we have

$$\begin{eqnarray}\displaystyle & & \displaystyle H(\text{Tor}_{i}(M,S/g(J)))(d)\nonumber\\ \displaystyle & & \displaystyle \qquad \;\;\quad =H(F_{i})(d)-H({\it\varphi}_{i}(F_{i})+g(J)F_{i-1})(d)+H(g(J)F_{i-1})(d)\nonumber\\ \displaystyle & & \displaystyle \qquad \;\;\qquad -\,H({\it\varphi}_{i+1}(F_{i+1})+g(J)F_{i})(d)\nonumber\end{eqnarray}$$

for all $d\in \mathbb{Z}$. Clearly $H(F_{i})$ and $H(g(J)F_{i-1})$ do not depend on $g.$ Then, in the same way as in the proof of Lemma 2.1, one can prove that there is a nonempty Zariski open subset $U\subset \text{GL}_{n}(K)$ such that the Hilbert function of ${\it\varphi}_{i}(F_{i})+g(J)F_{i-1}$ is maximal for any $g\in U$.◻

Note that Lemma 2.1 can be considered as a special case of the above proposition since $\text{Tor}_{0}(S/I,S/J)\cong S/(I+J)$ and $\text{Tor}_{0}(I,S/J)\cong I/IJ$.

For a vector $\mathbf{w}=(w_{1},\ldots ,w_{n})\in \mathbb{Z}_{{\geqslant}0}^{n}$, let $\text{in}_{\mathbf{w}}(I)$ be the initial ideal of a homogeneous ideal $I$ with respect to the weight order ${>}_{\mathbf{w}}$ (see [Ei, p. 345]). Let $T$ be a new indeterminate and $R=S[T]$. For $\mathbf{a}=(a_{1},\ldots ,a_{n})\in \mathbb{Z}_{{\geqslant}0}^{n}$, let $x^{\mathbf{a}}=x_{1}^{a_{1}}x_{2}^{a_{2}}\cdots x_{n}^{a_{n}}$ and $(\mathbf{a},\mathbf{w})=a_{1}w_{1}+\cdots +a_{n}w_{n}$. For a polynomial $f=\sum _{\mathbf{a}\in \mathbb{Z}_{{\geqslant}0}^{n}}c_{\mathbf{a}}x^{\mathbf{a}}$, where $c_{\mathbf{a}}\in K$, let $b=\max \{(\mathbf{a},\mathbf{w}):c_{\mathbf{a}}\neq 0\}$ and

$$\begin{eqnarray}\tilde{f}=T^{b}\left(\mathop{\sum }_{\mathbf{a}\in \mathbb{Z}_{{\geqslant}0}^{n}}T^{-(\mathbf{a},\mathbf{w})}c_{\boldsymbol{ a}}x^{\mathbf{a}}\right)\in R.\end{eqnarray}$$

Note that $\tilde{f}$ can be written as $\tilde{f}=\text{in}_{\mathbf{w}}(f)+Tg$ where $g\in R$. For an ideal $I\subset S$, let $\tilde{I} =(\tilde{f}:f\in I)\subset R$. For ${\it\lambda}\in K\setminus \{0\}$, let $D_{{\it\lambda},\mathbf{w}}$ be the diagonal change of coordinates defined by $D_{{\it\lambda},\mathbf{w}}(x_{i})={\it\lambda}^{-w_{i}}x_{i}$. From the definition, we have

$$\begin{eqnarray}R/\big(\tilde{I} +(T)\big)\cong S/\text{in}_{\mathbf{w}}(I)\end{eqnarray}$$

and

$$\begin{eqnarray}R/\big(\tilde{I} +(T-{\it\lambda})\big)\cong S/D_{{\it\lambda},\mathbf{w}}(I)\end{eqnarray}$$

where ${\it\lambda}\in K\setminus \{0\}$. Moreover, $(T-{\it\lambda})$ is a nonzero divisor of $R/\tilde{I}$ for any ${\it\lambda}\in K$. See [Ei, Section 15.8].

Lemma 2.3. Fix an integer $j$. Let $\mathbf{w}\in \mathbb{Z}_{{\geqslant}0}^{n}$, $M$ a finitely generated graded $S$-module and $J\subset S$ a homogeneous ideal. For a general ${\it\lambda}\in K$, one has

$$\begin{eqnarray}H\big(\text{Tor}_{i}\big(M,S/\text{in}_{\mathbf{w}}(J)\big)\big)(j)\geqslant H\big(\text{Tor}_{i}\big(M,S/D_{{\it\lambda},\mathbf{w}}(J)\big)\big)(j)\quad \text{for all }i.\end{eqnarray}$$

Proof. Consider the ideal $\tilde{J}\subset R$ defined as above. Let $\tilde{M}=M\otimes _{S}R$ and $T_{i}=\text{Tor}_{i}^{R}(\tilde{M},R/\tilde{J})$. By the structure theorem for modules over a PID (see [La, p. 149]), we have

$$\begin{eqnarray}(T_{i})_{j}\cong K[T]^{a_{ij}}\bigoplus A_{ij}\end{eqnarray}$$

as a finitely generated $K[T]$-module, where $a_{ij}\in \mathbb{Z}_{{\geqslant}0}$ and where $A_{ij}$ is the torsion submodule. Moreover, $A_{ij}$ is a module of the form

$$\begin{eqnarray}A_{ij}\cong \bigoplus _{h=1}^{b_{ij}}K[T]/(P_{h}^{i,j}),\end{eqnarray}$$

where $P_{h}^{i,j}$ is a nonzero polynomial in $K[T]$. Set $l_{{\it\lambda}}=T-{\it\lambda}$. Consider the exact sequence

By considering the long exact sequence induced by $\text{Tor}_{i}^{R}(\tilde{M},-)$, we have the following exact sequence

(3)$$\begin{eqnarray}0\longrightarrow T_{i}/l_{{\it\lambda}}T_{i}\longrightarrow \text{Tor}_{i}^{R}\big(\tilde{M},R/\big((l_{{\it\lambda}})+\tilde{J}\big)\big)\longrightarrow K_{i-1}\longrightarrow 0,\end{eqnarray}$$

where $K_{i-1}$ is the kernel of the map $T_{i-1}\xrightarrow[]{\cdot l_{{\it\lambda}}}T_{i-1}$. Since $l_{{\it\lambda}}$ is a regular element for $R$ and $\tilde{M}$, the middle term in (3) is isomorphic to

$$\begin{eqnarray}\displaystyle \text{Tor}_{i}^{R/(l_{{\it\lambda}})}\big(\tilde{M}/l_{{\it\lambda}}\tilde{M},R/\big((l_{{\it\lambda}})+\tilde{J}\big)\big)=\left\{\begin{array}{@{}ll@{}}\text{Tor}_{i}^{S}\big(M,S/\text{in}_{\boldsymbol{ w}}(J)\big) & \text{ if }{\it\lambda}=0,\\ \text{Tor}_{i}^{S}\big(M,S/D_{{\it\lambda},\mathbf{w}}(J)\big) & \text{ if }{\it\lambda}\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$

(see [Mat, p. 140]). By taking the graded component of degree $j$ in (3), we obtain

(4)$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\dim _{K}\text{Tor}_{i}^{S}\big(M,S/\text{in}_{\mathbf{w}}(J)\big)_{j}\ & =\ & a_{ij}+\#\{P_{h}^{ij}:P_{h}^{i,j}(0)=0\}\\ \ & \ & +\#\{P_{h}^{i-1,j}:P_{h}^{i-1,j}(0)=0\},\end{array} & & \displaystyle\end{eqnarray}$$

where $\#X$ denotes the cardinality of a finite set $X$, and

(5)$$\begin{eqnarray}\displaystyle \dim _{K}\text{Tor}_{i}^{S}\big(M,S/D_{{\it\lambda},\mathbf{w}}(J)\big)_{j} & = & \displaystyle a_{ij}\end{eqnarray}$$

for a general ${\it\lambda}\in K$. This proves the desired inequality.◻

Corollary 2.4. With the same notation as in Lemma 2.3, for a general ${\it\lambda}\in K$,

$$\begin{eqnarray}H\big(\text{Tor}_{i}\big(M,\text{in}_{\mathbf{w}}(J)\big)\big)(j)\geqslant H\big(\text{Tor}_{i}\big(M,D_{{\it\lambda},\mathbf{w}}(J)\big)\big)(j)\quad \text{for all }i.\end{eqnarray}$$

Proof. For any homogeneous ideal $I\subset S$, by considering the long exact sequence induced by $\text{Tor}_{i}(M,-)$ from the short exact sequence $0\longrightarrow I\longrightarrow S\longrightarrow S/I\longrightarrow 0$, we have

$$\begin{eqnarray}\text{Tor}_{i}(M,I)\cong \text{Tor}_{i+1}(M,S/I)\quad \text{for }i\geqslant 1\end{eqnarray}$$

and

$$\begin{eqnarray}\dim _{K}\!\text{Tor}_{0}(M,I)_{j}=\dim _{K}\!\text{Tor}_{1}(M,S/I)_{j}+\dim _{K}\!M_{j}-\dim _{K}\!\text{Tor}_{0}(M,S/I)_{j}.\end{eqnarray}$$

Thus, by Lemma 2.3 it is enough to prove that

$$\begin{eqnarray}\displaystyle \dim _{K} & & \displaystyle \!\!\text{Tor}_{1}\big(M,S/\text{in}_{\mathbf{w}}(J)\big)_{j}-\dim _{K}\text{Tor}_{1}\big(M,S/D_{{\it\lambda},\mathbf{w}}(J)\big)_{j}\nonumber\\ \displaystyle & & \displaystyle \geqslant \dim _{K}\text{Tor}_{0}\big(M,S/\text{in}_{\mathbf{w}}(J)\big)_{j}-\dim _{K}\text{Tor}_{0}\big(M,S/D_{{\it\lambda},\mathbf{w}}(J)\big)_{j}.\nonumber\end{eqnarray}$$

This inequality follows from (4) and (5).◻

Proposition 2.5. Fix an integer $j$. Let $I\subset S$ and $J\subset S$ be homogeneous ideals. Let $\mathbf{w},\mathbf{w}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{n}$. Then

1. (i) $H(\text{Tor}_{i},S/I,J)(j)\leqslant H(\text{Tor}_{i}(S/\text{in}_{\mathbf{w}}(I),S/\text{in}_{\mathbf{w}^{\prime }}(J)))(j)\text{ for all }i.$

2. (ii) $H(\text{Tor}_{i},I,J)(j)\leqslant H(\text{Tor}_{i}(\text{in}_{\mathbf{w}}(I),S/\text{in}_{\mathbf{w}^{\prime }}(J)))(j)\text{ for all }i.$

Proof. We prove (ii) (the proof for (i) is similar). By Lemma 2.3 and Corollary 2.4, we have

$$\begin{eqnarray}\displaystyle H\big(\text{Tor}_{i}\big(\text{in}_{\mathbf{w}}(I),S/\text{in}_{\mathbf{w}^{\prime }}(J)\big)\big)(j) & {\geqslant} & \displaystyle H\big(\text{Tor}_{i}\big(D_{{\it\lambda}_{1},\mathbf{w}}(I),S/D_{{\it\lambda}_{2},\mathbf{w}^{\prime }}(J)\big)\big)(j)\nonumber\\ \displaystyle & = & \displaystyle H(\text{Tor}_{i}\big(I,S/D_{{\it\lambda}_{1},\mathbf{w}}^{-1}\big(D_{{\it\lambda}_{2},\mathbf{w}^{\prime }}(J)\big)\big))(j)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle H(\text{Tor}_{i},S/I,J)(j),\nonumber\end{eqnarray}$$

as desired, where ${\it\lambda}_{1},{\it\lambda}_{2}$ are general elements in $K$.◻

Remark 2.6. Let $\mathbf{w}^{\prime }=(1,1,\ldots ,1)$ and note that the composite of two general changes of coordinates is still general. By replacing $J$ by $g(J)$ for a general change of coordinates $g,$ from Proposition 2.5(i) it follows that

$$\begin{eqnarray}H(\text{Tor}_{i}(S/I,S/g(J)))(j)\leqslant H(\text{Tor}_{i}(S/\text{in}_{{>}_{{\it\sigma}}}(I),S/g(J)))(j)\end{eqnarray}$$

for any term order ${>}_{{\it\sigma}}$.

The above fact gives, as a special case, an affirmative answer to [Co2, Question 6.1]. This was originally proved in the thesis of the first author [Ca2]. We mention it here because there seem to be no published article which includes the proof of this fact.

Theorem 2.7. Fix an integer $j$. Let $I\subset S$ and $J\subset S$ be homogeneous ideals, and let ${>}_{{\it\sigma}}$ and ${>}_{{\it\tau}}$ be term orders. Then

1. (i) $H(\text{Tor}_{i},S/I,J)(j)\leqslant H(\text{Tor}_{i}(S/\text{Gin}_{{\it\sigma}}(I),S/\text{Gin}_{{\it\tau}}(J)))(j)\text{ for all }i$.

2. (ii) $H(\text{Tor}_{i},I,J)(j)\leqslant H(\text{Tor}_{i}(\text{Gin}_{{\it\sigma}}(I),S/\text{Gin}_{{\it\tau}}(J)))(j)\text{ for all }i$.

Proof. Without loss of generality, we may assume $\text{in}_{{\it\sigma}}(I)=\text{Gin}_{{\it\sigma}}(I)$ and that $\text{in}_{{\it\tau}}(J)=\text{Gin}_{{\it\tau}}(J)$. It follows from [Ei, Proposition 15.16] that there are vectors $\mathbf{w},\mathbf{w}^{\prime }\in \mathbb{Z}_{{\geqslant}0}^{n}$ such that $\text{in}_{\mathbf{w}}(I)=\text{in}_{{\it\sigma}}(I)$ and $\text{in}_{\mathbf{w}^{\prime }}(J)=\text{Gin}_{{\it\tau}}(J)$. Then the desired inequality follows from Proposition 2.5.◻

We later use the following special case of Theorem 2.7.

Corollary 2.8. Let $I\subset S$ and $J\subset S$ be homogeneous ideals. Then

1. (i) $H(\cap ,I,J)(d)\leqslant H(\text{Gin}_{\text{lex}}(I)\cap \text{Gin}_{\text{oplex}}(J))(d)$ for all $d\geqslant 0$.

2. (ii) $H(\cdot ,I,J)(d)\geqslant H(\text{Gin}_{\text{lex}}(I)\text{Gin}_{\text{oplex}}(J))(d)$ for all $d\geqslant 0$.

We conclude this section with a result regarding the Krull dimension of certain Tor modules. We show how Theorem 2.7 can be used to give a quick proof of Proposition 2.9, which is a special case (for the variety $X=\mathbb{P}^{n-1}$ and the algebraic group $SL_{n}$) of the main Theorem of [MSp].

Let $B_{+}\subset \text{GL}_{n}(K)$ (resp. $B_{-}\subset \text{GL}_{n}(K)$) be the set of the nonsingular upper triangular (resp. lower triangular) matrixes. For a group $G\subset \text{GL}_{n}(K)$, a homogeneous ideal $I\subset S$ is said to be $G$-fixed if $b(I)=I$ for any $b\in G$. Recall that, for an ideal $I$ of $S$, $\text{Gin}_{\text{lex}}(I)$ is $B_{+}$-fixed and $\text{Gin}_{\text{oplex}}(I)$ is $B_{-}$-fixed. See [Ei, Section 15.9] for more details on the combinatorial properties of $B_{+}$-fixed ideals.

Let $I$ and $J$ be ideals generated by linear forms. If we assume that $I$ is $B_{+}$-fixed and that $J$ is $B_{-}$-fixed, then there exist $1\leqslant i,j\leqslant n$ such that $I=(x_{1},\ldots ,x_{i})$ and $J=(x_{j},\ldots ,x_{n}).$ An easy computation shows that the Krull dimension of $\text{Tor}_{i}(S/I,S/J)$ is always zero when $i>0.$

More generally one has

Proposition 2.9. (Miller–Speyer)

Let $M$ be a finitely generated graded $S$-module, and let $J$ be a homogeneous ideal of $S.$ For a general change of coordinates $g$, the Krull dimension of $\text{Tor}_{i}(M,S/g(J))$ is zero for all $i>0.$

Proof. By considering a filtration $M=M_{k}\supset M_{k-1}\supset \cdots \supset M_{1}\supset 0$ such that $M_{k}/M_{k-1}\cong S/P_{k}$ for some prime ideal $P_{k}$ (see [Ei, Proposition 3.7]), it is enough to consider the case when $M=S/I$ for some homogeneous ideal $I$. By Theorem 2.7, we may assume that $I$ is $B_{+}$-fixed and $J$ is $B_{-}$-fixed. Since an associated prime ideal of $B_{+}$-fixed ideal is an ideal of the form $(x_{1},\ldots ,x_{a})$ [Ei, Corollary 15.25], by considering filtrations of $S/I$ and $S/J$, one may assume $I=(x_{1},\ldots ,x_{a})$ and $J=(x_{b},\ldots ,x_{n})$. This proves the desired property.◻

3 General intersections and general products

In this section, we prove Theorems 1.3 and 1.4. We assume throughout the rest of the paper $\text{char}(K)=0.$

A monomial ideal $I\subset S$ is said to be 0-Borel (or strongly stable) if, for every monomial $ux_{j}\in I$ and for every $1\leqslant i<j$ one has $ux_{i}\in I$. Note that$0$-Borel ideals are precisely all the possible $B_{+}$-fixed ideals in characteristic $0$. In general, the $B_{+}$-fixed property depends on the characteristic of the field and we refer the readers to [Ei, Section 15.9] for the details. A set $W\subset S$ of monomials in $S$ is said to be 0-Borel if for every monomial $ux_{j}\in W$ and for every $1\leqslant i<j$ one has $ux_{i}\in W$. Similarly we say that a monomial ideal $J\subset S$ is opposite 0-Borel if for every monomial $ux_{j}\in J$ and for every $j<i\leqslant n$ one has $ux_{i}\in J$.

Let ${>}_{\text{rev}}$ be the reverse lexicographic order induced by the ordering $x_{1}>\cdots >x_{n}$. We recall the following result [Mu, Lemma 3.2].

Lemma 3.1. Let $V=\{v_{1},\ldots ,v_{s}\}\subset S_{d}$ be a $0$-Borel set of monomials and $W=\{w_{1},\ldots ,w_{s}\}\subset S_{d}$ the lex-segment set of monomials, where $v_{1}\geqslant _{\text{rev}}\cdots \geqslant _{\text{rev}}v_{s}$ and $w_{1}\geqslant _{\text{rev}}\cdots \geqslant _{\text{rev}}w_{s}$. Then $v_{i}\geqslant _{\text{rev}}w_{i}$ for all $i=1,2,\ldots ,s$.

Since generic initial ideals with respect to ${>}_{\text{lex}}$ are $0$-Borel, the next lemma and Corollary 2.8(i) prove Theorem 1.3.

Lemma 3.2. Let $I\subset S$ be a $0$-Borel ideal and $P\subset S$ an opposite lex-segment ideal. Then $H(I\cap P)(d)\leqslant H(I^{\text{lex}}\cap P)(d)$ for all $d\geqslant 0$.

Proof. Fix a degree $d$. Let $V,W$ and $Q$ be the sets of monomials of degree $d$ in $I$, $I^{\text{lex}}$ and $P$, respectively. It is enough to prove that $\#V\cap Q\leqslant \#W\cap Q$.

Observe that $Q$ is the set of the smallest $\#Q$ monomials in $S_{d}$ with respect to ${>}_{\text{rev}}$. Let $m=\max _{{>}_{\text{rev}}}Q$. Then by Lemma 3.1

$$\begin{eqnarray}\#V\cap Q=\#\{v\in V:v\leqslant _{\text{rev}}m\}\leqslant \#\{w\in W:w\leqslant _{\text{rev}}m\}=\#W\cap Q,\end{eqnarray}$$

as desired. ◻

Next, we consider products of ideals. For a monomial $u\in S$, let $\max u$ (resp., $\min u$) be the maximal (resp., minimal) integer $i$ such that $x_{i}$ divides $u$, where we set $\max 1=1$ and $\min 1=n$. For a monomial ideal $I\subset S$, let $I_{({\leqslant}k)}$ be the $K$-vector space spanned by all monomials $u\in I$ with $\max u\leqslant k$.

Lemma 3.3. Let $I\subset S$ be a $0$-Borel ideal and $P\subset S$ an opposite $0$-Borel ideal. Let $G(P)=\{u_{1},\ldots ,u_{s}\}$ be the set of the minimal monomial generators of $P$. As a $K$-vector space, $IP$ is the direct sum

$$\begin{eqnarray}IP=\bigoplus _{i=1}^{s}(I_{({\leqslant}\min u_{i})})u_{i}.\end{eqnarray}$$

Proof. It is enough to prove that, for any monomial $w\in IP$, there is the unique expression $w=f(w)g(w)$ with $f(w)\in I$ and $g(w)\in P$ satisfying

1. (a) $\max f(w)\leqslant \min g(w)$.

2. (b) $g(w)\in G(P)$.

Given any expression $w=fg$ such that $f\in I$ and $g\in P$, since $I$ is $0$-Borel and $P$ is opposite $0$-Borel, if $\max f>\min g$ then we may replace $f$ by $f\frac{x_{\min g}}{x_{\max f}}\in I$ and replace $g$ by $g\frac{x_{\max f}}{x_{\min g}}\in P$. This fact shows that there is an expression satisfying (a) and (b).

Suppose that the expressions $w=f(w)g(w)$ and $w=f^{\prime }(w)g^{\prime }(w)$ satisfy conditions (a) and (b). Then, by (a), $g(w)$ divides $g^{\prime }(w)$ or $g^{\prime }(w)$ divides $g(w)$. Since $g(w)$ and $g^{\prime }(w)$ are generators of $P$, $g(w)=g^{\prime }(w)$. Hence the expression is unique.◻

Lemma 3.4. Let $I\subset S$ be a $0$-Borel ideal and $P\subset S$ an opposite $0$-Borel ideal. Then $H(IP)(d)\geqslant H(I^{\text{lex}}P)(d)$ for all $d\geqslant 0$.

Proof. Lemma 3.1 shows that $\dim _{K}{I_{({\leqslant}k)}}_{d}\geqslant \dim _{K}{I_{({\leqslant}k)}^{\text{lex}}}_{d}$ for all $k$ and $d\geqslant 0$. Then the statement follows from Lemma 3.3.◻

Finally we prove Theorem 1.4.

Proof of Theorem 1.4.

Let $I^{\prime }=\text{Gin}_{\text{lex}}(I)$ and $J^{\prime }=\text{Gin}_{\text{oplex}}(J)$. Since $I^{\prime }$ is $0$-Borel and $J^{\prime }$ is opposite $0$-Borel, by Corollary 2.8(ii) and Lemma 3.4

$$\begin{eqnarray}H(Ig(J))(d)\geqslant H(I^{\prime }J^{\prime })(d)\geqslant H(I^{\text{lex}}J^{\prime })(d)\geqslant H(I^{\text{lex}}J^{\text{oplex}})(d)\end{eqnarray}$$

for all $d\geqslant 0$.◻

Remark 3.5. Theorems 1.3 and 1.4 are sharp. Let $I\subset S$ be a $B_{+}$-fixed ideal and $J\subset S$ a $B_{-}$-fixed ideal. For a general $g\in \text{GL}_{n}(K)$, we have the LU decomposition $g=bb^{\prime }$ where $b\in B_{+}$ and $b^{\prime }\in B_{-}$. Then

$$\begin{eqnarray}H(\cap ,I,J)=H(I\cap g(J))=H(b^{-1}(I)\cap b^{\prime }(J))=H(I\cap J)\end{eqnarray}$$

and similarly

$$\begin{eqnarray}H(\cdot ,IJ)=H(b(I)b^{\prime }(J))=H(IJ).\end{eqnarray}$$

Thus, if $I$ is a lex-segment ideal and $J$ is an opposite lex-segment ideal then we have equalities in Theorems 1.3 and 1.4.

Remark 3.6. The assumption on $\text{Gin}_{\text{lex}}(J)$ in Theorem 1.3 is necessary. Let $I=(x_{1}^{3},x_{1}^{2}x_{2},x_{1}x_{2}^{2},x_{2}^{3})\subset K[x_{1},x_{2},x_{3}]$ and $J=(x_{3}^{2},x_{3}^{2}x_{2},x_{3}x_{2}^{2},x_{2}^{3})\subset K[x_{1},x_{2},x_{3}]$. Then

$$\begin{eqnarray}I^{\text{lex}}=(x_{1}^{3},x_{1}^{2}x_{2},x_{1}^{2}x_{3},x_{1}x_{2}^{2},x_{1}x_{2}x_{3}^{2},x_{1}x_{3}^{4},x_{2}^{6})\end{eqnarray}$$

and $J^{\text{oplex}}$ is obtained from $I^{\text{lex}}$ by exchanging $x_{1}$ and $x_{3}$. Then $H(I^{\text{lex}}\cap J^{\text{oplex}})(3)=0$. On the other hand, as we see in Remark 3.5, $H(I\cap g(J))(3)=H(I\cap J)(3)=1$. Similarly, the assumption on the characteristic of $K$ is needed as one can easily see by considering $\text{char}(K)=p>0$, $I=(x_{1}^{p},x_{2}^{p})\subset K[x_{1},x_{2}]$ and $J=(x_{2}^{p}).$ In this case we have $H((I^{\prime })^{\text{lex}}\cap (J^{\prime })^{\text{oplex}})(p)=0$, while $H(I^{\prime }\cap g(J^{\prime }))(p)=H(g^{-1}(I^{\prime })\cap J^{\prime })(p)=1$ since $I$ is fixed under any change of coordinates.

Remark 3.7. Let $h:\mathbb{Z}\rightarrow \mathbb{Z}$ and $h^{\prime }:\mathbb{Z}\rightarrow \mathbb{Z}$ be Hilbert functions of homogeneous ideals of $S$. One may ask if, there are ideals $L$ and $L^{\prime }$ such that $H(L)=h$, $H(L^{\prime })=h^{\prime }$ and

$$\begin{eqnarray}H(\cap ,L,L^{\prime })(d)=\max \{H(\cap ,I,J)(d):H(I)=h,~H(J)=h^{\prime }\}\end{eqnarray}$$

for all $d$. Corollary 2.8 and Remark 3.5 say that to study this question, one may assume that $L$ is $B_{+}$-fixed,$L^{\prime }$ is $B_{-}$-fixed and $H(\cap ,L,L^{\prime })=H(L\cap L^{\prime })$.

Unfortunately, not all Hilbert functions $h$ and $h^{\prime }$ satisfy this property. Let $I$ and $J$ be ideals given in Remark 3.6 and $h=H(I)=H(J)$. Then

$$\begin{eqnarray}\max \{H(\cap ,I^{\prime },J^{\prime })(3):H(I^{\prime })=H(J^{\prime })=h\}=1.\end{eqnarray}$$

Also, if $L$ is $B_{+}$-fixed, $L^{\prime }$ is $B_{-}$-fixed and $H(L\cap L^{\prime })(3)=1$, then we have $L=I$ and $L^{\prime }=J$. However,

$$\begin{eqnarray}H(I\cap J)(5)=9<10=H(I^{\text{lex}}\cap J^{\text{lex}})(5).\end{eqnarray}$$

Since $\text{Tor}_{0}(S/I,S/J)\cong S/(I+J)$ and $\text{Tor}_{1}(S/I,S/J)\cong (I\cap J)/IJ$ for all homogeneous ideals $I\subset S$ and $J\subset S$, Theorems 1.3 and 1.4 show the next statement.

Remark 3.8. Conjecture 1.5 is true if $i=0$ or $i=1.$

It would be of interest to study lower bounds of the Hilbert functions of the modules $\text{Tor}_{i}(S/I,S/J)$ and $\text{Ext}^{i}(S/I,S/J)$. For example, it was asked in [MSt, Problem 18.35] which monomial ideal $I$ minimize the $K$-dimension of $\text{Hom}(I,S/I)$ among all monomial ideals $I\subset S$ of co-length $n$. At the moment, we are not sure if the techniques used in this paper is applicable to this problem.