ON HARMONIC AND PSEUDOHARMONIC MAPS FROM PSEUDO-HERMITIAN MANIFOLDS

Abstract

In this paper, we give some rigidity results for both harmonic and pseudoharmonic maps from pseudo-Hermitian manifolds into Riemannian manifolds or Kähler manifolds. Some foliated results, pluriharmonicity and Siu–Sampson type results are established for both harmonic maps and pseudoharmonic maps.

1 Introduction

In 1980, Siu [20] studied the strong rigidity of compact Kähler manifolds by using the theory of harmonic maps. The basic discovery by Siu was a new Bochner-type formula for harmonic maps between Kähler manifolds, which does not involve the Ricci curvature tensor of the domains. Using the modified Bochner formula, he proved that all harmonic maps from a compact Kähler manifold to a Kähler manifold with strongly seminegative curvature are actually pluriharmonic and some curvature expressions vanish. When the target manifolds are Kähler manifolds with strongly negative curvature or compact quotients of irreducible bounded symmetric domains, the vanishing curvature terms, under the assumption of sufficiently high rank, force the maps to be either holomorphic or antiholomorphic. Later, Sampson [19] showed that all harmonic maps from compact Kähler manifolds into Riemannian manifolds with nonpositive Hermitian curvature are also pluriharmonic, which generalized the pluriharmonicity result of Siu to more general targets. Pluriharmonic maps, holomorphic maps and Siu–Sampson type results have many important applications in geometry and topology of Kähler manifolds. The readers are referred to [23] for details.

In 2002, Petit [16] established some rigidity results for harmonic maps from strictly pseudoconvex CR manifolds, endowed with a positively oriented contact form, to Kähler manifolds and Riemannian manifolds by using tools of spinorial geometry. First, he proved that any harmonic map $\unicode[STIX]{x1D719}:M\rightarrow N$ from a compact Sasakian manifold to a Riemannian manifold with nonpositive sectional curvature satisfies that $d\unicode[STIX]{x1D719}(T)=0$ , where $T$ is the characteristic direction of $(M,\unicode[STIX]{x1D703})$ . A map with this property will be called foliated. Next he proved that under suitable rank conditions the harmonic map from a compact Sasakian manifold to a Kähler manifold with strongly negative curvature is $(J,J^{N})$ -holomorphic or anti- $(J,J^{N})$ -holomorphic. However, Petit [16] did not specifically discuss the relevant notions of pluriharmonicity. On the other hand, Barletta et al. in [1] introduced the so-called pseudoharmonic maps from nondegenerate CR manifolds which are a natural generalization of harmonic maps. In his thesis [4], Chang discussed some fundamental properties of pseudoharmonic maps.

In this paper, we establish some rigidity results for both harmonic maps and pseudoharmonic maps from pseudo-Hermitian manifolds by using the moving frame method. First, we find a result about the relationship between harmonic maps and pseudoharmonic maps from pseudo-Hermitian manifolds, which claims that these two kinds of maps are actually equivalent if the maps are foliated. By the moving frame method, we not only recapture Petit’s result about harmonic maps from compact Sasakian manifolds to Riemannian manifolds with nonpositive curvature (Theorem 5.2), but also show that the result is still valid for pseudoharmonic maps (Theorem 5.1).

The usual Bochner-type formula for the energy density of harmonic maps was given in [10]. In [4], Chang derived the CR Bochner-type formula for the horizontal energy density of a pseudoharmonic map  $\unicode[STIX]{x1D719}$ . Unlike the Bochner formula of harmonic maps, there is a mixed term $\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$ appearing in the CR Bochner formula for the pseudoharmonic map (cf. Lemma 4.1). When $\unicode[STIX]{x1D719}$ is a function, it is known that the CR Paneitz operator, which is a divergence of a third order differential operator $P$ , is a useful tool to treat such kind of term. One important property of the CR Paneitz operator is its nonnegativity when the dimension of the CR manifold ${\geqslant}5$ (cf. [5]). We generalize the operator $P$ to a differential operator, still denoted by $P$ , acting on maps from a pseudo-Hermitian manifolds into a Riemannian manifold, and establish similar nonnegativity under the assumptions that the domain manifold has dimension ${\geqslant}5$ and the target manifold is of nonpositive Hermitian curvature (Theorem 4.1). This enables us to establish a CR Bochner-type result for pseudoharmonic maps (Theorem 4.2).

As mentioned previously, the notion of “pluriharmonicity” is important for Siu–Sampson type results and other potential applications. We shall discuss suitable notion of pluriharmonic maps from pseudo-Hermitian manifolds. On a pseudo-Hermitian manifold, we have two canonical connections, that is, the Levi-Civita connection of the Webster metric and the Tanaka–Webster connection of the pseudo-Hermitian structure. As a result, there are two kinds of second fundamental forms for a map from a pseudo-Hermitian manifold to a Riemannian manifold: the usual second fundamental form $B$ and a new second fundamental form $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ . The later one is defined with respect to the Tanaka–Webster connection of the domain pseudo-Hermitian manifold and the Levi-Civita connection of the target Riemannian manifold (see Section 2). Using $B$ , Ianus and Pastore [13] defined two kinds of pluriharmonic notions. In [8], Dragomir and Kamishima introduced the notion of $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map by means of $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ . It turns out that a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map is pseudoharmonic and foliated, and thus it is harmonic too. In addition, when the target manifold is Kähler, the $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic maps in [8] are more compatible with the $(J,J^{N})$ -holomorphic maps in the sense that all $(J,J^{N})$ -holomorphic maps are automatically $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic. Next, using the Siu–Sampson technique, we prove that all harmonic maps or pseudoharmonic maps from compact Sasakian manifolds to Riemannian manifolds with nonpositive Hermitian curvature or Kähler manifolds with strong seminegative curvature are $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic (Theorems 6.1, 6.2). If the target is a Kähler manifold with strongly negative curvature and the rank of the map ${\geqslant}3$ at some point, then the harmonic map or the pseudoharmonic map is $(J,J^{N})$ -holomorphic or anti- $(J,J^{N})$ -holomorphic (Theorem 7.3). In [16], Petit proved a similar result for harmonic maps using different technique. When the target is a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor, we show that the harmonic or pseudoharmonic maps are $(J,J^{N})$ -holomorphic under some explicit rank conditions (Theorem 7.1). These generalize some similar results in [3] to the pseudo-Hermitian case. To derive the above results, we also investigate the conic extensions of harmonic maps, $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic maps and $(J,J^{N})$ -holomorphic maps from Sasakian manifolds respectively, and establish also a unique continuation theorem for $(J,J^{N})$ -holomorphicity (Proposition 7.2). Using a technique in [17], we consider harmonic maps and pseudoharmonic maps from complete noncompact pseudo-Hermitian manifolds too. Under some decay conditions, some foliated results and $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonicity results are given.

Finally, we would like to mention that Yuxin Dong in [7] has established similar rigidity results including Siu type results for pseudoharmonic maps between pseudo-Hermitian manifolds.

2 Preliminaries

2.1 Pseudo-Hermitian structures

A smooth manifold $M$ of real $(2m+1)$ -dimension is said to be a CR manifold (of type $(m,1)$ ) if there exists a smooth $m$ -dimensional complex subbundle $T_{1,0}(M)$ of the complexifed tangent bundle $T^{\mathbb{C}}(M)=T(M)\otimes \mathbb{C}$ , such that

$$\begin{eqnarray}T_{1,0}(M)\cap T_{0,1}(M)=\{0\}\end{eqnarray}$$

and

$$\begin{eqnarray}Z,W\in \unicode[STIX]{x1D6E4}^{\infty }(U,T_{1,0}(M))\Rightarrow [Z,W]\in \unicode[STIX]{x1D6E4}^{\infty }(U,T_{1,0}(M))\end{eqnarray}$$

for any open subset $U\subset M$ . Here $T_{0,1}(M)=\overline{T_{1,0}(M)}$ denotes the complex conjugate of $T_{1,0}(M)$ . The subbundle $T_{1,0}(M)$ is called a CR structure on  $M$ . Equivalently, the CR structure may also be described by the Levi distribution $H(M)=\text{Re}\{T_{1,0}(M)\oplus T_{0,1}(M)\}$ , which carries a complex structure $J:H(M)\rightarrow H(M)$ given by

$$\begin{eqnarray}J(Z+\bar{Z})=\sqrt{-1}(Z-\bar{Z}),\end{eqnarray}$$

for any $Z\in T_{1,0}(M)$ .

Hereafter we assume $M$ is orientable. Let us set

$$\begin{eqnarray}E_{x}=\{\unicode[STIX]{x1D714}\in T_{x}^{\ast }(M):\text{Ker}(\unicode[STIX]{x1D714})\supseteq H_{x}(M)\},\end{eqnarray}$$

for any $x\in M$ . Then $E\rightarrow M$ becomes an orientable real line subbundle of the cotangent bundle $T^{\ast }(M)$ , and thus there exist globally defined nonvanishing sections $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E4}^{\infty }(E)$ . Any such a section $\unicode[STIX]{x1D703}$ is called a pseudo-Hermitian structure on $M$ . The Levi form $G_{\unicode[STIX]{x1D703}}$ of $\unicode[STIX]{x1D703}$ is defined by

$$\begin{eqnarray}G_{\unicode[STIX]{x1D703}}(X,Y)=d\unicode[STIX]{x1D703}(X,JY),\end{eqnarray}$$

for any $X,Y\in H(M)$ . A CR manifold $(M,T_{1,0}(M))$ is said to be a strictly pseudoconvex CR manifold if the Levi form $G_{\unicode[STIX]{x1D703}}$ is positive definite for some pseudo-Hermitian structure $\unicode[STIX]{x1D703}$ on  $M$ . Standard examples of strictly pseudoconvex CR manifolds are the odd-dimensional spheres and the Heisenberg groups.

When $(M,T_{1,0}(M))$ is strictly pseudoconvex, it is natural to orient $E$ by declaring a pseudo-Hermitian structure $\unicode[STIX]{x1D703}$ to be positive if $G_{\unicode[STIX]{x1D703}}$ is positive definite. Henceforth we shall assume that $(M,T_{1,0}(M))$ is strictly pseudoconvex and $\unicode[STIX]{x1D703}$ is a positive pseudo-Hermitian structure. The triple $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ is called a pseudo-Hermitian manifold.

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold. Then there exists a unique nonvanishing vector field $T$ on $M$ , transverse to $H(M)$ , satisfying $\unicode[STIX]{x1D703}(T)=1$ and $T\lrcorner \,d\unicode[STIX]{x1D703}=0$ . The vector field $T$ is referred to as the characteristic direction or the Reeb vector field of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ . Then we can extend $G_{\unicode[STIX]{x1D703}}$ to a Riemannian metric $g_{\unicode[STIX]{x1D703}}$ , called the Webster metric, on $M$ as follows:

$$\begin{eqnarray}g_{\unicode[STIX]{x1D703}}(X,Y)=G_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D70B}_{H}X,\unicode[STIX]{x1D70B}_{H}Y)+\unicode[STIX]{x1D703}(X)\unicode[STIX]{x1D703}(Y),\end{eqnarray}$$

for any $X,Y\in T(M)$ , where $\unicode[STIX]{x1D70B}_{H}:T(M)\rightarrow H(M)$ is the projection associated to the direct sum decomposition $T(M)=H(M)\oplus \mathbb{R}T$ . Let us extend $J$ to a $(1,1)$ tensor field on $M$ by requesting that $JT=0$ . Then the two-form $\unicode[STIX]{x1D6FA}$ defined by $\unicode[STIX]{x1D6FA}(X,Y)=g_{\unicode[STIX]{x1D703}}(X,JY)$ coincides with the two-form $-d\unicode[STIX]{x1D703}$ . Thus the pseudo-Hermitian manifold $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ carries a contact metric structure $(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$ (cf. [9]).

On a pseudo-Hermitian manifold, there exists a canonical linear connection preserving both the CR structure and the Webster metric.

Lemma 2.1. (cf. [9, 22, 26])

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $g_{\unicode[STIX]{x1D703}}$ the Webster metric of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ . Then there exists a unique linear connection $\unicode[STIX]{x1D6FB}$ on $M$ , called the Tanaka–Webster connection, such that:

1. (1) the Levi distribution $H(M)$ is parallel with respect to  $\unicode[STIX]{x1D6FB}$ ;

2. (2) $\unicode[STIX]{x1D6FB}g_{\unicode[STIX]{x1D703}}=0$ , $\unicode[STIX]{x1D6FB}J=0$ , $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D703}=0$ (hence $\unicode[STIX]{x1D6FB}T=0$ );

3. (3) the torsion $T_{\unicode[STIX]{x1D6FB}}$ of $\unicode[STIX]{x1D6FB}$ satisfies $T_{\unicode[STIX]{x1D6FB}}(X,Y)=-2\unicode[STIX]{x1D6FA}(X,Y)T$ and $T_{\unicode[STIX]{x1D6FB}}(T,JX)=-JT_{\unicode[STIX]{x1D6FB}}(T,X)$ , for any $X,Y\in H(M)$ .

Unlike the Levi-Civita connection, the torsion $T_{\unicode[STIX]{x1D6FB}}$ of the Tanaka–Webster connection $\unicode[STIX]{x1D6FB}$ is always nonzero. The pseudo-Hermitian torsion of $\unicode[STIX]{x1D6FB}$ , denoted by $\unicode[STIX]{x1D70F}$ , is defined by $\unicode[STIX]{x1D70F}(X)=T_{\unicode[STIX]{x1D6FB}}(T,X)$ , for any $X\in T(M)$ . Note that $\unicode[STIX]{x1D70F}$ is trace-free and self-adjoint with respect to the Webster metric $g_{\unicode[STIX]{x1D703}}$ (cf. [9]). Let us set

$$\begin{eqnarray}A(X,Y)=g_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D70F}X,Y),\end{eqnarray}$$

for any $X,Y\in T(M)$ . Then we have $A(X,Y)=A(Y,X)$ .

Theorem 2.1. (cf. [9])

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold. Then the Webster metric $g_{\unicode[STIX]{x1D703}}$ is Sasakian if and only if the Tanaka–Webster connection of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ has vanishing pseudo-Hermitian torsion, that is, $\unicode[STIX]{x1D70F}=0$ .

Remark 2.1. In the following of this paper, a pseudo-Hermitian manifold $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ is said to be a Sasakian manifold, if the Webster metric $g_{\unicode[STIX]{x1D703}}$ is Sasakian. The quadruple $(J,-T,-\unicode[STIX]{x1D703},g_{\unicode[STIX]{x1D703}})$ is referred to as a Sasakian structure on $M$ . The readers are referred to [2] for the original definition of Sasakian metrics.

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold. Let $\{T_{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$ be a local frame of $T_{1,0}(M)$ defined on an open set $U\subset M$ and $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}:1\leqslant \unicode[STIX]{x1D6FC}\leqslant m\}$ the corresponding admissible local coframe, that is, $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FD}})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$ , $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T_{\bar{\unicode[STIX]{x1D6FD}}})=0$ , $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}(T)=0$ . Clearly Lemma 2.1 implies that there exist unique locally defined complex 1-forms $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$ such that

$$\begin{eqnarray}\unicode[STIX]{x1D6FB}T_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}\otimes T_{\unicode[STIX]{x1D6FD}},\qquad \unicode[STIX]{x1D6FB}T_{\bar{\unicode[STIX]{x1D6FC}}}=\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{\unicode[STIX]{x1D6FD}}}\otimes T_{\bar{\unicode[STIX]{x1D6FD}}},\end{eqnarray}$$

where $T_{\bar{\unicode[STIX]{x1D6FC}}}=\overline{T_{\unicode[STIX]{x1D6FC}}}$ and $\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}}$ . These are the connection 1-forms of the Tanaka–Webster connection $\unicode[STIX]{x1D6FB}$ . Since $\unicode[STIX]{x1D70F}(T_{1,0}(M))\subset T_{0,1}(M)$ , there are uniquely defined smooth functions $A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}:U\rightarrow \mathbb{C}$ such that

$$\begin{eqnarray}\unicode[STIX]{x1D70F}(T_{\unicode[STIX]{x1D6FC}})=A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}T_{\bar{\unicode[STIX]{x1D6FD}}}.\end{eqnarray}$$

Writing $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$ and $h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=g_{\unicode[STIX]{x1D703}}(T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})$ , we have $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FE}}}h_{\bar{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}}$ . Let us define the local 1-forms $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\ast }(M)\otimes \mathbb{C})$ by setting $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}=A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}$ . Then $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}\otimes T_{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes T_{\bar{\unicode[STIX]{x1D6FC}}}$ , where $\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FC}}}=\overline{\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}}$ .

The Tanaka–Webster connection induces a covariant differential operator $\unicode[STIX]{x1D6FB}$ on tensors on  $M$ . We denote components of covariant derivatives with indices preceded by a comma; for instance, $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FE}}}=(\unicode[STIX]{x1D6FB}_{T_{\bar{\unicode[STIX]{x1D6FE}}}}A)(T_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FD}})$ and $A_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}^{\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}[(\unicode[STIX]{x1D6FB}_{T_{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D70F})(T_{\unicode[STIX]{x1D6FC}})]$ . The indices $\{0,\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}\}$ indicate derivatives with respect to $\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$ . For derivatives of a scalar function, we omit the comma; for example, $u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\overline{\bar{u}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}}=T_{\bar{\unicode[STIX]{x1D6FD}}}T_{\unicode[STIX]{x1D6FC}}u-\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}(T_{\bar{\unicode[STIX]{x1D6FD}}})T_{\unicode[STIX]{x1D6FE}}u$ and $u_{00}=TTu$ . Then we have the following structure equations for the Tanaka–Webster connection  $\unicode[STIX]{x1D6FB}$ .

Lemma 2.2. (cf. [9, 26])

The structure equations for the Tanaka–Webster connection of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ in terms of local coframe $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$ are

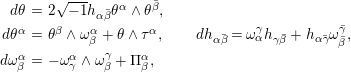(2.1) $$\begin{eqnarray}\qquad \begin{array}{@{}rcl@{}}d\unicode[STIX]{x1D703}\ & =\ & 2\sqrt{-1}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\\ d\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\ & =\ & \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}},\qquad dh_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}+h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D714}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}},\\ d\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\ & =\ & -\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}},\end{array}\end{eqnarray}$$

where

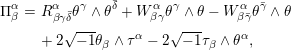(2.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}} & = & \displaystyle R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FF}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FF}}}+W_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FE}}\wedge \unicode[STIX]{x1D703}-W_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FE}}}\wedge \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}-2\sqrt{-1}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$

with

(2.3) $$\begin{eqnarray}W_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D6FD}}=h^{\bar{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}}A_{\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FF}},\unicode[STIX]{x1D6FC}},\qquad W_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FD}}=h^{\bar{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6FD}}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE},\bar{\unicode[STIX]{x1D6FF}}},\qquad \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}=h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D70F}^{\bar{\unicode[STIX]{x1D6FD}}},\qquad \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}=h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\end{eqnarray}$$

and $(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$ is the inverse matrix of the matrix $(h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}})$ .

Let us set by definition $R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=g_{\unicode[STIX]{x1D703}}(R(T_{\unicode[STIX]{x1D706}},T_{\bar{\unicode[STIX]{x1D707}}})T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FD}}})=h_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FE}}$ , where $R$ is the curvature tensor of $\unicode[STIX]{x1D6FB}$ . From (2.1), one may derive that (cf. [26]): $R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}$ . The pseudo-Hermitian Ricci tensor is given by $R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}=R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}^{\unicode[STIX]{x1D6FC}}$ , which satisfies $R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}=R_{\bar{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D706}}$ . Since the Tanaka–Webster connection can be viewed as a connection in $T_{1,0}(M)$ , the pseudo-Hermitian Ricci tensor and the torsion tensor on $T_{1,0}(M)$ are also denoted by

$$\begin{eqnarray}\text{Ric}(X,Y)=R_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}X^{\unicode[STIX]{x1D6FC}}Y^{\bar{\unicode[STIX]{x1D6FD}}}\end{eqnarray}$$

and

$$\begin{eqnarray}\text{Tor}(X,Y)=\sqrt{-1}(A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}X^{\bar{\unicode[STIX]{x1D6FC}}}Y^{\bar{\unicode[STIX]{x1D6FD}}}-A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}X^{\unicode[STIX]{x1D6FC}}Y^{\unicode[STIX]{x1D6FD}})\end{eqnarray}$$

for any $X=X^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$ , $Y=Y^{\unicode[STIX]{x1D6FD}}T_{\unicode[STIX]{x1D6FD}}\in T_{1,0}(M)$ .

The divergence of a vector field $X$ on $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ is defined by

$$\begin{eqnarray}\mathscr{L}_{X}\unicode[STIX]{x1D6F9}=\text{div}(X)\unicode[STIX]{x1D6F9},\end{eqnarray}$$

where $\mathscr{L}_{X}$ denotes the Lie derivative and $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$ is, up to a constant, the volume form on $(M,g_{\unicode[STIX]{x1D703}})$ . The divergence $\text{div}(X)$ can be computed in another way, that is,

$$\begin{eqnarray}\text{div}(X)=\text{trace}_{g_{\unicode[STIX]{x1D703}}}\{Y\in T(M)\mapsto \unicode[STIX]{x1D6FB}_{Y}X\}.\end{eqnarray}$$

If $Z=Z^{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$ , then $\text{div}(Z)=T_{\unicode[STIX]{x1D6FC}}(Z^{\unicode[STIX]{x1D6FC}})+Z^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D6FC}})$ . For a 1-form $\unicode[STIX]{x1D70E}$ on $M$ , we denote by $X_{\unicode[STIX]{x1D70E}}$ its dual vector field, that is, $g_{\unicode[STIX]{x1D703}}(X_{\unicode[STIX]{x1D70E}},Y)=\unicode[STIX]{x1D70E}(Y)$ for any $Y\in T(M)$ . The divergence of $\unicode[STIX]{x1D70E}$ denoted by $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})$ is defined by $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\text{div}(X_{\unicode[STIX]{x1D70E}})$ . If $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}$ , then $\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FD}}}h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}$ . The sublaplacian of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ is the differential operator $\unicode[STIX]{x1D6E5}_{b}$ on functions defined by

$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{b}u=-\text{div}(\unicode[STIX]{x1D6FB}^{H}u),\end{eqnarray}$$

for any $u\in C^{2}(M)$ . Here $\unicode[STIX]{x1D6FB}^{H}u=\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FB}u$ is the horizontal gradient, and $\unicode[STIX]{x1D6FB}u$ is the ordinary gradient of $u$ with respect to the Webster metric $g_{\unicode[STIX]{x1D703}}$ , that is, $g_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u,X)=X(u)$ for any $X\in T(M)$ . With respect to the local frame $\{T,T_{\unicode[STIX]{x1D6FC}},T_{\bar{\unicode[STIX]{x1D6FC}}}\}$ , the sublaplacian $\unicode[STIX]{x1D6E5}_{b}$ can be expressed as $\unicode[STIX]{x1D6E5}_{b}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}})$ .

We denote by $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$ the Levi-Civita connection of $(M,g_{\unicode[STIX]{x1D703}})$ . From [9, Lemma 1.3], we know that the Levi-Civita connection $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$ is related to the Tanaka–Webster connection $\unicode[STIX]{x1D6FB}$ by

(2.4) $$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D6FB}+(\unicode[STIX]{x1D6FA}-A)\otimes T+\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D703}+2\unicode[STIX]{x1D703}\odot J,\end{eqnarray}$$

where $2(\unicode[STIX]{x1D703}\odot J)(X,Y)=\unicode[STIX]{x1D703}(X)JY+\unicode[STIX]{x1D703}(Y)JX$ . By (2.4), we have $\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D70F}(X)+JX$ . In particular, $\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=0$ . If $X,Y\in H(M)$ , then

(2.5) $$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}Y=\unicode[STIX]{x1D6FB}_{X}Y+[\unicode[STIX]{x1D6FA}(X,Y)-A(X,Y)]T.\end{eqnarray}$$

Since $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D6FB}$ is a $(1,2)$ tensor field on $M$ and $\unicode[STIX]{x1D6FB}_{T}^{\unicode[STIX]{x1D703}}T=\unicode[STIX]{x1D6FB}_{T}T=0$ , we can define a vector field $V$ on $M$ given by

$$\begin{eqnarray}V=\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D6FB})=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}-\unicode[STIX]{x1D6FB}).\end{eqnarray}$$

Actually we have $V=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70F})T=0$ . On the Riemannian manifold $(M,g_{\unicode[STIX]{x1D703}})$ , the Laplace–Beltrami operator is given by $\unicode[STIX]{x1D6E5}u=-\text{trace}_{g_{\unicode[STIX]{x1D703}}}\{Y\in T(M)\mapsto \unicode[STIX]{x1D6FB}_{Y}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FB}u)\}$ for any $u\in C^{2}(M)$ . Since $V=0$ , we have $\unicode[STIX]{x1D6E5}u=-\text{div}(\unicode[STIX]{x1D6FB}u)$ and $\unicode[STIX]{x1D6E5}u=-(h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}u_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}u_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}+u_{00})$ .

2.2 Harmonic maps and pseudoharmonic maps

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold ( $g_{\unicode[STIX]{x1D703}}$ is positive definite). Let us denote by $\unicode[STIX]{x1D6FB}$ and $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}$ the Tanaka–Webster connection of $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ and the Levi-Civita connection of the Webster metric $g_{\unicode[STIX]{x1D703}}$ , respectively. Let $(N,h)$ be a Riemannian manifold with the Levi-Civita connection $\unicode[STIX]{x1D6FB}^{h}$ . For a smooth map $\unicode[STIX]{x1D719}:M\rightarrow N$ , there are two induced connections $\unicode[STIX]{x1D6FB}^{\unicode[STIX]{x1D703}}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$ and $\unicode[STIX]{x1D6FB}\otimes \unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$ on $T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$ . Using these two connections, one may define the usual second fundamental form $B(\unicode[STIX]{x1D719})$ and a new second fundamental form $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ (cf. [16]) for the map $\unicode[STIX]{x1D719}$ as follows:

(2.6) $$\begin{eqnarray}B(\unicode[STIX]{x1D719})(X,Y)=\unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(X))-d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}^{\unicode[STIX]{x1D703}}X)\end{eqnarray}$$

and

(2.7) $$\begin{eqnarray}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)=\unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(X))-d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}X),\end{eqnarray}$$

for any $X,Y\in T(M)$ , where $\unicode[STIX]{x1D719}^{-1}\unicode[STIX]{x1D6FB}^{h}$ is written as $\unicode[STIX]{x1D6FB}^{h}$ for simplicity. While $B(\unicode[STIX]{x1D719})$ is symmetric on $T(M)\otimes T(M)$ , $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ is, in general, nonsymmetric.

For any bilinear form $C$ on $T(M)$ , we denote by $\unicode[STIX]{x1D70B}_{H}C$ the restriction of $C$ to $H(M)\otimes H(M)$ . Recall that $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ is pseudoharmonic if the vector field along $\unicode[STIX]{x1D719}$ given by $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719}))$ vanishes. In [1], the pseudoharmonic map is the critical point of the horizontal energy functional

(2.8) $$\begin{eqnarray}E_{H,\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D719})=\int _{\unicode[STIX]{x1D6FA}}e_{H}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D6F9},\end{eqnarray}$$

for any $\unicode[STIX]{x1D6FA}\subset \subset M$ , where $e_{H}(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D719}^{\ast }h)$ is the horizontal energy density and $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D703}\wedge (d\unicode[STIX]{x1D703})^{m}$ . Let $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$ be the usual tension field of $\unicode[STIX]{x1D719}$ given by $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=\text{trace}_{g_{\unicode[STIX]{x1D703}}}B(\unicode[STIX]{x1D719})$ . Then $\unicode[STIX]{x1D719}:(M,g_{\unicode[STIX]{x1D703}})\rightarrow (N,h)$ is harmonic if and only if $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$ (cf. [10]). Due to $V=0$ , we have

(2.9) $$\begin{eqnarray}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719}))=\text{trace}_{G_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D70B}_{H}B(\unicode[STIX]{x1D719})),\end{eqnarray}$$

and

(2.10) $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=\text{trace}_{g_{\unicode[STIX]{x1D703}}}B(\unicode[STIX]{x1D719})=\text{trace}_{g_{\unicode[STIX]{x1D703}}}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719}).\end{eqnarray}$$

A smooth map $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ is said to be a foliated map if $d\unicode[STIX]{x1D719}(T)=0$ .

Proposition 2.1. (cf. [25])

Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. Let $\unicode[STIX]{x1D719}:M\rightarrow (N,h)$ be a smooth map. Then

$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})+\unicode[STIX]{x1D6FB}_{T}^{h}\,d\unicode[STIX]{x1D719}(T).\end{eqnarray}$$

If in addition $\unicode[STIX]{x1D719}$ is foliated, then $\unicode[STIX]{x1D719}$ is harmonic if and only if it is pseudoharmonic.

Definition 2.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be a smooth map. We say that:

1. (i) [13] $\unicode[STIX]{x1D719}$ is $J$ -pluriharmonic, if $B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$ , for any $X,Y\in T(M)$ ;

2. (ii) [13] $\unicode[STIX]{x1D719}$ is $H(M)$ -pluriharmonic, if $B(\unicode[STIX]{x1D719})(X,Y)+B(\unicode[STIX]{x1D719})(JX,JY)=0$ , for any $X,Y\in H(M)$ ;

3. (iii) [8] $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic, if $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY)=0$ , for any $X,Y\in H(M)$ ;

4. (iv) [11] when $(N,h)$ is a Kähler manifold with complex structure $J^{N}$ , $\unicode[STIX]{x1D719}$ is called a $(J,J^{N})$ -holomorphic (resp. anti- $(J,J^{N})$ -holomorphic) map, if

   (2.11) $$\begin{eqnarray}d\unicode[STIX]{x1D719}\circ J=J^{N}\circ d\unicode[STIX]{x1D719},\quad (\text{resp.}~d\unicode[STIX]{x1D719}\circ J=-J^{N}\circ d\unicode[STIX]{x1D719}).\end{eqnarray}$$

Obviously, both the $J$ -pluriharmonic map and the $(J,J^{N})$ -holomorphic map are harmonic (cf. [11, 13]). By (2.9), the $H(M)$ -pluriharmonic map is pseudoharmonic. Dragomir and Kamishima in [8] proved that every $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map is a pseudoharmonic map. Actually, we get that any $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map is foliated.

Proposition 2.2. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. If $\unicode[STIX]{x1D719}:M\rightarrow N$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic, then $\unicode[STIX]{x1D719}$ is a foliated map.

Proof. For any $Z=X-\sqrt{-1}JX$ , $W=Y-\sqrt{-1}JY\in T_{1,0}(M)$ , we have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W}) & = & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY)\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}[\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,JY)-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,Y)],\nonumber\end{eqnarray}$$

and

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{Z},W) & = & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY)\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}[\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,JY)-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,Y)].\nonumber\end{eqnarray}$$

Thus we get that $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic if and only if $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{Z},W)=0$ for any $Z,W\in T_{1,0}(M)$ . Therefore, any $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map is pseudoharmonic.

If $\unicode[STIX]{x1D719}:M\rightarrow N$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic, then we have

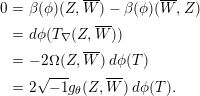(2.12) $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Z,\overline{W})-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(\overline{W},Z)\nonumber\\ \displaystyle & = & \displaystyle d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FB}}(Z,\overline{W}))\nonumber\\ \displaystyle & = & \displaystyle -2\unicode[STIX]{x1D6FA}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T)\nonumber\\ \displaystyle & = & \displaystyle 2\sqrt{-1}g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\,d\unicode[STIX]{x1D719}(T).\end{eqnarray}$$

If we take $Z=W\neq 0$ , then $g_{\unicode[STIX]{x1D703}}(Z,\overline{W})\neq 0$ , thus we have $d\unicode[STIX]{x1D719}(T)=0$ .◻

Proposition 2.3. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $(N,h)$ a Kähler manifold with complex structure  $J^{N}$ . Suppose $\unicode[STIX]{x1D719}:\rightarrow N$ is a $\pm (J,J^{N})$ -holomorphic map. Then $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic.

Proof. Without loss of generality, we assume that $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic. Since $J^{N}\,d\unicode[STIX]{x1D719}(T)=d\unicode[STIX]{x1D719}(JT)=0$ , we get that $\unicode[STIX]{x1D719}$ is foliated. Because of the following identity

$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y)-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Y,X)=d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FB}}(X,Y))=-2\unicode[STIX]{x1D6FA}(X,Y)\,d\unicode[STIX]{x1D719}(T),\end{eqnarray}$$

for any $X,Y\in H(M)$ , we get that $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ is symmetric on $H(M)\otimes H(M)$ . On the other hand, we have

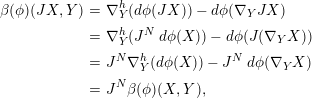(2.13) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,Y) & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(JX))-d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}JX)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{Y}^{h}(J^{N}\,d\unicode[STIX]{x1D719}(X))-d\unicode[STIX]{x1D719}(J(\unicode[STIX]{x1D6FB}_{Y}X))\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FB}_{Y}^{h}(d\unicode[STIX]{x1D719}(X))-J^{N}\,d\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FB}_{Y}X)\nonumber\\ \displaystyle & = & \displaystyle J^{N}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y),\end{eqnarray}$$

for any $X,Y\in H(M)$ . Thus we have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JX,JY) & = & \displaystyle J^{N}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,JY)=J^{N}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(JY,X)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(Y,X)=-\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(X,Y).\nonumber\end{eqnarray}$$

Therefore, the $(J,J^{N})$ -holomorphic map $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic.◻

3 Commutation relations

Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold. Let $(N,h)$ be a Riemannian manifold with the Levi-Civita connection $\unicode[STIX]{x1D6FB}^{h}$ . Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be a smooth map. Choose a local admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ on $M$ and a local orthonormal coframe field $\{\unicode[STIX]{x1D70E}^{i}\}$ on  $N$ . Throughout this paper we employ the index conventions

$$\begin{eqnarray}\displaystyle & A,B,C=0,1,\ldots ,m,\bar{1},\ldots ,\bar{m}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}=1,\ldots ,m, & \displaystyle \nonumber\\ \displaystyle & i,j,k=1,\ldots ,n, & \displaystyle \nonumber\end{eqnarray}$$

and use the summation convention on repeating indices. The structure equations for the Levi-Civita connection $\unicode[STIX]{x1D6FB}^{h}$ of $(N,h)$ in terms of local orthonormal coframe field $\{\unicode[STIX]{x1D70E}^{i}\}$ are

$$\begin{eqnarray}d\unicode[STIX]{x1D70E}^{i}=-\unicode[STIX]{x1D702}_{j}^{i}\wedge \unicode[STIX]{x1D70E}^{j},\qquad \unicode[STIX]{x1D702}_{j}^{i}+\unicode[STIX]{x1D702}_{i}^{j}=0,\end{eqnarray}$$

(3.1) $$\begin{eqnarray}d\unicode[STIX]{x1D702}_{j}^{i}=-\unicode[STIX]{x1D702}_{k}^{i}\wedge \unicode[STIX]{x1D702}_{j}^{k}+\unicode[STIX]{x1D6FA}_{j}^{i},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FA}_{j}^{i}=(1/2)\widehat{R}_{jkl}^{i}\unicode[STIX]{x1D70E}^{k}\wedge \unicode[STIX]{x1D70E}^{l}$ are the curvature forms of  $\unicode[STIX]{x1D6FB}^{h}$ .

Under the map $\unicode[STIX]{x1D719}:M\rightarrow N$ , we denote the components of $d\unicode[STIX]{x1D719}$ , the covariant derivatives $\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$ and $\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$ with respect to the local frames $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\}$ and $\{\unicode[STIX]{x1D70E}^{i}\}$ by $\unicode[STIX]{x1D719}_{A}^{i}$ , $\unicode[STIX]{x1D719}_{AB}^{i}$ and $\unicode[STIX]{x1D719}_{ABC}^{i}$ respectively, that is,

$$\begin{eqnarray}\displaystyle d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{A}^{i}\unicode[STIX]{x1D703}^{A}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{AB}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes E_{i},\nonumber\\ \displaystyle \unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719} & = & \displaystyle \unicode[STIX]{x1D719}_{ABC}^{i}\unicode[STIX]{x1D703}^{A}\otimes \unicode[STIX]{x1D703}^{B}\otimes \unicode[STIX]{x1D703}^{C}\otimes E_{i},\nonumber\end{eqnarray}$$

where $\unicode[STIX]{x1D703}^{0}=\unicode[STIX]{x1D703}$ and $\{E_{i}\}$ is the dual vector field of $\{\unicode[STIX]{x1D70E}^{i}\}$ . Thus we have

(3.2) $$\begin{eqnarray}\unicode[STIX]{x1D719}^{\ast }\unicode[STIX]{x1D70E}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D703}.\end{eqnarray}$$

Hereafter we drop $\unicode[STIX]{x1D719}^{\ast }$ in such formulas when their meaning is clear from the context.

By taking the exterior derivative of (3.2) and making use of the structure equations (2.1) and (3.1), we get

(3.3) $$\begin{eqnarray}D\unicode[STIX]{x1D719}_{B}^{i}\wedge \unicode[STIX]{x1D703}^{B}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}\wedge \unicode[STIX]{x1D703}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D703}=0,\end{eqnarray}$$

where

(3.4) $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i} & \equiv & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}B}^{i}\unicode[STIX]{x1D703}^{B},\end{eqnarray}$$

(3.5) $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i} & \equiv & \displaystyle d\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}B}^{i}\unicode[STIX]{x1D703}^{B},\end{eqnarray}$$

(3.6) $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{0}^{i} & \equiv & \displaystyle d\unicode[STIX]{x1D719}_{0}^{i}+\unicode[STIX]{x1D719}_{0}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0B}^{i}\unicode[STIX]{x1D703}^{B}.\end{eqnarray}$$

Then (3.3) gives

(3.7) $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i},\qquad \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}=2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}},\qquad \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}.\end{eqnarray}$$

Then the map $\unicode[STIX]{x1D719}$ is harmonic if and only if

$$\begin{eqnarray}h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{00}^{i}=0,\end{eqnarray}$$

and $\unicode[STIX]{x1D719}$ is pseudoharmonic if and only if

$$\begin{eqnarray}h^{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}+h^{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}=0.\end{eqnarray}$$

Differentiating the equation (3.4) and using the structure equations in $M$ and $N$ , we have

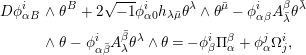(3.8) $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}B}^{i} & \wedge & \displaystyle \unicode[STIX]{x1D703}^{B}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}h_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D707}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D706}}}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & \wedge & \displaystyle \unicode[STIX]{x1D703}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D706}}^{\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D706}}\wedge \unicode[STIX]{x1D703}=-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D6FA}_{j}^{i},\end{eqnarray}$$

where

$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FE}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}0}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$

From (3.8), we get the following commutation relations

(3.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FE}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}},\end{eqnarray}$$

(3.10) $$\begin{eqnarray}\displaystyle \qquad \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}A_{\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D706}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}},\end{eqnarray}$$

(3.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D706}}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}h_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FE}}},\end{eqnarray}$$

(3.12) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}0}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h^{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D707}}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{i}A_{\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D6FE}}},\end{eqnarray}$$

(3.13) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}0}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jkl}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h^{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D707}}}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$

Similarly the exterior derivative of (3.6) yields

(3.14) $$\begin{eqnarray}D\unicode[STIX]{x1D719}_{0B}^{i}\wedge \unicode[STIX]{x1D703}^{B}+2\sqrt{-1}\unicode[STIX]{x1D719}_{00}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}\wedge \unicode[STIX]{x1D703}-\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D6FC}}}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\wedge \unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}_{0}^{j}\unicode[STIX]{x1D6FA}_{j}^{i},\end{eqnarray}$$

where

$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D703}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}B}^{i}\unicode[STIX]{x1D703}^{B},\nonumber\\ \displaystyle D\unicode[STIX]{x1D719}_{00}^{i} & = & \displaystyle d\unicode[STIX]{x1D719}_{00}^{i}+\unicode[STIX]{x1D719}_{00}^{j}\unicode[STIX]{x1D702}_{j}^{i}=\unicode[STIX]{x1D719}_{00B}^{i}\unicode[STIX]{x1D703}^{B}.\nonumber\end{eqnarray}$$

We get from (3.14) the commutation relations

(3.15) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{0}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i},\end{eqnarray}$$

(3.16) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{0}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{00}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}},\end{eqnarray}$$

(3.17) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{00\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}0}^{i}-\unicode[STIX]{x1D719}_{0}^{j}\unicode[STIX]{x1D719}_{0}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FD}}}.\end{eqnarray}$$

From (3.7), we can derive:

(3.18) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FE}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{i}+2\sqrt{-1}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FE}}^{i},\end{eqnarray}$$

(3.19) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}^{i}+2\sqrt{-1}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FE}}}^{i},\end{eqnarray}$$

(3.20) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FE}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{i}A_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D6FE}}},\end{eqnarray}$$

(3.21) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D6FE}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{i}A_{\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FD}}}^{\bar{\unicode[STIX]{x1D6FE}}}.\end{eqnarray}$$

If $(N,h)$ is a Kähler manifold, we choose a local orthonormal coframe field $\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}=\overline{\widetilde{\unicode[STIX]{x1D714}}^{i}}\}$ on  $N$ . The structure equations for the Levi-Civita connection of $(N,h)$ in terms of local orthonormal frame $\{\widetilde{\unicode[STIX]{x1D714}}^{i},\widetilde{\unicode[STIX]{x1D714}}^{\bar{i}}\}$ are

(3.22) $$\begin{eqnarray}\begin{array}{@{}c@{}}d\widetilde{\unicode[STIX]{x1D714}}^{i}=-\widetilde{\unicode[STIX]{x1D714}}_{j}^{i}\wedge \widetilde{\unicode[STIX]{x1D714}}^{j},\qquad \widetilde{\unicode[STIX]{x1D714}}_{j}^{i}+\widetilde{\unicode[STIX]{x1D714}}_{\bar{i}}^{\bar{j}}=0,\\ d\widetilde{\unicode[STIX]{x1D714}}_{j}^{i}=-\widetilde{\unicode[STIX]{x1D714}}_{k}^{i}\wedge \widetilde{\unicode[STIX]{x1D714}}_{j}^{k}+\widetilde{\unicode[STIX]{x1D6FA}}_{j}^{i},\end{array}\end{eqnarray}$$

where $\widetilde{\unicode[STIX]{x1D6FA}}_{j}^{i}=\widetilde{R}_{jk\overline{l}}^{i}\widetilde{\unicode[STIX]{x1D714}}^{k}\wedge \widetilde{\unicode[STIX]{x1D714}}^{\bar{l}}$ . Similar to the above discussions, we may obtain the following commutation formula:

(3.23) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FE}}}^{i} & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FE}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{jk\bar{l}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}A_{\bar{\unicode[STIX]{x1D6FE}}}^{\unicode[STIX]{x1D706}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}h_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FE}}}A_{\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}.\end{eqnarray}$$

4 CR Bochner-type result

Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$ be a smooth map. We choose a local orthonormal admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ on $M$ , a local orthonormal coframe field $\{\unicode[STIX]{x1D70E}^{i}\}$ on $N$ . We still use the notations of the last section. Denote

$$\begin{eqnarray}\displaystyle & d_{b}\unicode[STIX]{x1D719}=d\unicode[STIX]{x1D719}|_{H(M)}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\otimes E_{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}}\otimes E_{i}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|_{H(M)}=(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i})\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\otimes E_{i}+(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}}\otimes E_{i}, & \displaystyle \nonumber\end{eqnarray}$$

where $\{E_{i}\}$ is the dual vector field of $\{\unicode[STIX]{x1D70E}^{i}\}$ .

We first derive the following CR Bochner formula.

Lemma 4.1. Set $\widehat{R}_{ijkl}=h_{jp}\widehat{R}_{ikl}^{p}=\unicode[STIX]{x1D6FF}_{jp}\widehat{R}_{ikl}^{p}=\widehat{R}_{ikl}^{j}$ . Then

(4.1) $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})+\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})-4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}),\end{eqnarray}$$

where $\langle \langle \cdot ,\cdot \rangle \rangle$ is the metric in $T^{\ast }(M)\otimes \unicode[STIX]{x1D719}^{-1}T(N)$ induced by $g_{\unicode[STIX]{x1D703}}$ and  $h$ .

Proof. From the definition of the components of $\unicode[STIX]{x1D6FB}\,d\unicode[STIX]{x1D719}$ and $\unicode[STIX]{x1D6FB}^{2}\,d\unicode[STIX]{x1D719}$ , it is easy to get that

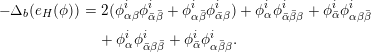$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$

By the commutation relations of Section 3, we have

$$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}R_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{\bar{\unicode[STIX]{x1D706}}}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}R_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jkl}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jkl}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}})\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}}^{\unicode[STIX]{x1D706}})-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}}^{\bar{\unicode[STIX]{x1D706}}}))\nonumber\\ \displaystyle & = & \displaystyle 2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}R_{\unicode[STIX]{x1D706}\bar{\unicode[STIX]{x1D6FC}}}}^{i}-2m\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D706}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & & \displaystyle -\,4\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}).\nonumber\end{eqnarray}$$

The main difficulty in applications of Lemma 4.1 comes from the mixed term $\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})$ . It is known that the CR Paneitz operator is a useful tool to deal with such a term. In [12, 14] the authors introduced the following differential operator acting on functions

$$\begin{eqnarray}Pf=(f_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}+2\sqrt{-1}mA_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}f_{\bar{\unicode[STIX]{x1D6FC}}})\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}=(P_{\unicode[STIX]{x1D6FD}}f)\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}},\end{eqnarray}$$

which characterizes CR pluriharmonic functions on $M$ (cf. also [9, Chapter 5]). In [5] Chang and Chiu discussed the CR Paneitz operator

$$\begin{eqnarray}P_{0}f=4\unicode[STIX]{x1D6FF}_{b}(Pf+\overline{Pf}),\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}_{b}$ is the divergence operator that takes 1-forms to functions, and they proved that when $m\geqslant 2$ , the corresponding CR Paneitz operator is always nonnegative, that is

$$\begin{eqnarray}\int _{M}P_{0}f\cdot f\unicode[STIX]{x1D6F9}=-4\int _{M}g_{\unicode[STIX]{x1D703}}(Pf+\overline{Pf},d_{b}f)\unicode[STIX]{x1D6F9}\geqslant 0.\end{eqnarray}$$

We generalize the operator $P$ to an operator, still denoted by $P$ , acting on maps from compact pseudo-Hermitian manifolds into Riemannian manifolds. Define

$$\begin{eqnarray}P\unicode[STIX]{x1D719}=(P_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719})\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}\otimes E_{j},\end{eqnarray}$$

where $P_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{j}+2\sqrt{-1}mA_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}$ . From the definition of $\unicode[STIX]{x1D719}_{A}^{i}$ , $\unicode[STIX]{x1D719}_{AB}^{i}$ and $\unicode[STIX]{x1D719}_{ABC}^{i}$ , we can see that the definition of the operator $P$ is independent of the choice of the local admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ and local frame field $\{E_{i}\}$ , thus the operator $P$ is well-defined.

Lemma 4.2.

(4.2) $$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$

Proof. From (3.19), we have

(4.3) $$\begin{eqnarray}\sqrt{-1}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}=\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}).\end{eqnarray}$$

Then (3.7) and (4.3) imply

$$\begin{eqnarray}\displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i} & = & \displaystyle \sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i})-\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}-\frac{1}{2m}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}.\nonumber\end{eqnarray}$$

After taking the conjugation of the above formula, we obtain

$$\begin{eqnarray}-\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}=\frac{1}{2m}P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}-\frac{1}{2m}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}.\end{eqnarray}$$

Consequently, we get

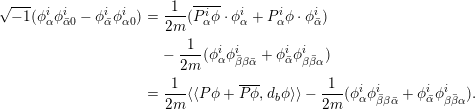(4.4) $$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \frac{1}{2m}(\overline{P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}}\cdot \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}+P_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle -\frac{1}{2m}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}).\end{eqnarray}$$

On the other hand, one can derive the following:

$$\begin{eqnarray}\displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i})+\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$

Therefore, we have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i} & = & \displaystyle \langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$

We complete the proof by substituting the above formula into (4.4).◻

Thus the CR Bochner formula could be refreshed by the following corollary.

Corollary 4.1.

(4.5) $$\begin{eqnarray}\displaystyle -\unicode[STIX]{x1D6E5}_{b}(e_{H}(\unicode[STIX]{x1D719})) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\nonumber\\ \displaystyle & & \displaystyle +\left(1+\frac{2}{m}\right)\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m+2)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle \nonumber\\ \displaystyle & & \displaystyle -\,2(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}).\end{eqnarray}$$

In order to apply the above CR Bochner formula, we want to investigate the sign of the integral of the term $\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}\rangle \rangle$ . We now state two lemmas.

Lemma 4.3.

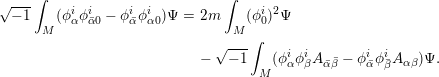(4.6) $$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle 2m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Proof. From (3.7) we can derive the following equality:

$$\begin{eqnarray}\displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}) & = & \displaystyle \sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$

Integrating both sides of the above formula and using the divergence theorem, we obtain

$$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$

By (3.7), we have

$$\begin{eqnarray}-\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}=2m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

The proof is completed by combining the above two formulas. ◻

Lemma 4.4.

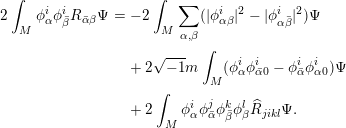(4.7) $$\begin{eqnarray}\displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9} & = & \displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Proof. From (3.11), we have

$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}R_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\unicode[STIX]{x1D706}}+2\sqrt{-1}m\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}.\end{eqnarray}$$

Hence

$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\nonumber\\ \displaystyle & & \displaystyle \quad =2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}m(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i}).\nonumber\end{eqnarray}$$

Using the divergence theorem, we derive

$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle \quad =-2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$

Consequently

$$\begin{eqnarray}\displaystyle -2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}-|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9} & = & \displaystyle 2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}R_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6F9}-2\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$

This completes the proof of Lemma 4.4. ◻

We can establish the nonnegative property of the generalized operator $P$ under suitable conditions. Recall that a Riemannian manifold $(N^{n},h)$ is said to have nonpositive Hermitian curvature if

(4.8) $$\begin{eqnarray}h(\widehat{R}(\overline{X},\overline{Y})Y,X)\leqslant 0,\end{eqnarray}$$

for any $X,Y\in T(N)\otimes \mathbb{C}$ (cf. [19]).

Theorem 4.1. Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact pseudo-Hermitian manifold with $m\geqslant 2$ and $(N,h)$ a Riemannian manifold with nonpositive Hermitian curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is a smooth map, then

$$\begin{eqnarray}-\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}\geqslant 0.\end{eqnarray}$$

Proof. Integrating (4.1) on $M$ and substituting (4.7) into it, we have

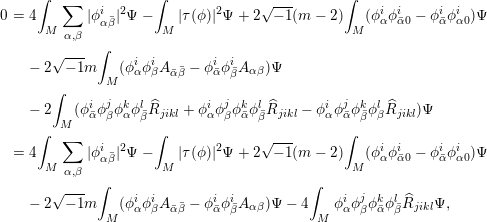(4.9) $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\!\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle 4\!\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\!\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}+2\sqrt{-1}(m-2)\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}m\!\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}-4\!\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

where the second equality follows from the Bianchi identity. Integrating both sides of (4.2) and using the divergence theorem, we get

(4.10) $$\begin{eqnarray}\displaystyle \sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle \frac{1}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}+\frac{1}{2m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Calculating (4.10) ×  $2(m-1)$  - (4.6) × 2 and substituting the result into (4.9), we have

(4.11) $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 4\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}-\frac{1}{m}\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}-4m\int _{M}(\unicode[STIX]{x1D719}_{0}^{i})^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2(m-1)}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}-4\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Since

$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\geqslant \frac{1}{m}\left|\sum \mathop{\unicode[STIX]{x1D719}}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\right|^{2}=\frac{1}{4m}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}+m(\unicode[STIX]{x1D719}_{0}^{i})^{2},\end{eqnarray}$$

we conclude

(4.12) $$\begin{eqnarray}-\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}\geqslant -\frac{2m}{m-1}\int _{M}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\unicode[STIX]{x1D6F9}\geqslant 0.\end{eqnarray}$$

Combing this theorem with Corollary 4.1, we obtain the following CR Bochner-type result.

Theorem 4.2. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact pseudo-Hermitian manifold with $m\geqslant 2$ and $(N,h)$ a Riemannian manifold with nonpositive Hermitian curvature. Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be a pseudoharmonic map. Suppose that

(4.13) $$\begin{eqnarray}(\text{Ric}-(m+2)\text{Tor})(Z,Z)\geqslant 0,\end{eqnarray}$$

for any $Z\in \unicode[STIX]{x1D6E4}^{\infty }(T_{1,0}M)$ , then $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$ for any $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ . In particular, $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic.

Proof. From (4.5), we have

$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle 2\int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}-\left(1+\frac{2}{m}\right)\int _{M}|\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{m}\int _{M}\langle \langle P\unicode[STIX]{x1D719}+\overline{P\unicode[STIX]{x1D719}},d_{b}\unicode[STIX]{x1D719}\rangle \rangle \unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{M}(\text{Ric}-(m+2)\text{Tor})((\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}},(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & & \displaystyle -\,2\int _{M}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl})\unicode[STIX]{x1D6F9},\nonumber\end{eqnarray}$$

where $(\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D719}^{i})_{\mathbb{C}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}T_{\unicode[STIX]{x1D6FC}}$ . By Theorem 4.1, the third term on the right-hand side of the preceding equation is nonnegative. Because of the curvature condition of  $N$ , the last term on the right-hand side is nonnegative. Since $\unicode[STIX]{x1D719}$ is pseudoharmonic, from (4.13) we get

$$\begin{eqnarray}0\geqslant \int _{M}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}(|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2})\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Hence $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$ . From $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=0$ , we see that $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic.◻

Corollary 4.2. If the manifold $M$ in Theorem 4.2 is Sasakian and $\text{Ric}(Z,Z)\geqslant 0$ , then we have $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})\equiv 0$ .

5 Foliated results of harmonic and pseudoharmonic maps

Let $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$ be a smooth map from a pseudo-Hermitian manifold into a Riemannian manifold. To obtain the foliated results for the map $\unicode[STIX]{x1D719}:M\rightarrow N$ , we consider the sublaplacian and the Laplacian of the square norm of $d\unicode[STIX]{x1D719}(T)$ , respectively.

We choose a local orthonormal admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ on $M$ and a local orthonormal coframe field $\{\unicode[STIX]{x1D70E}^{i}\}$ on  $N$ . By the commutation relations of Section 3, we have

Lemma 5.1.

(5.1) $$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}});\end{eqnarray}$$

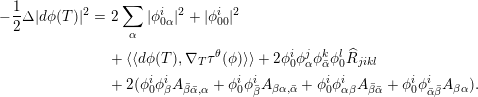(5.2) $$\begin{eqnarray}\displaystyle -\frac{1}{2}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\langle \langle d\unicode[STIX]{x1D719}(T),\unicode[STIX]{x1D6FB}_{T}\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})\rangle \rangle +2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$

Proof. Using (3.21), (3.13), (3.7) and their complex conjugate, we compute

$$\begin{eqnarray}\displaystyle -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2} & = & \displaystyle (\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FC}}}+(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}0\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{i}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}0}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}0}^{i})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$

Since the formula for $-(1/2)\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}$ can be derived similarly, we omit the details.◻

Lemma 5.2. Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be a smooth map. If the second fundamental form satisfies

$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0\quad \text{for any}~X\in H(M),\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is foliated.

Proof. By the integration by parts and the commutation formulas (3.7), we have

$$\begin{eqnarray}\displaystyle 0=\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i})\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{M}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{0}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{0}^{i})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle m\int _{M}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}.\nonumber\end{eqnarray}$$

Thus we have $\unicode[STIX]{x1D719}_{0}^{i}=0$ , that is, $d\unicode[STIX]{x1D719}(T)=0$ .◻

First, we prove the following result by the moving frame method.

Theorem 5.1. Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is a pseudoharmonic map. Then $\unicode[STIX]{x1D719}$ is foliated.

Proof. Since $\unicode[STIX]{x1D719}$ is pseudoharmonic, we have $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=0$ . The Sasakian condition for $M$ implies that $A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=0$ , for any $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ . Thus (5.1) becomes

$$\begin{eqnarray}-\frac{1}{2}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2}=2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{0}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{l}\widehat{R}_{jikl}.\end{eqnarray}$$

Since the sectional curvature of $N$ is nonpositive, we take $T_{\unicode[STIX]{x1D6FC}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}})$ and $T_{\bar{\unicode[STIX]{x1D6FC}}}=(1/\sqrt{2})(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}})$ and compute the following curvature term to find

(5.3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{0}^{l}\widehat{R}_{jikl} & = & \displaystyle h(\widehat{R}(d\unicode[STIX]{x1D719}(T_{\bar{\unicode[STIX]{x1D6FC}}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}+iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}-iJe_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}\! [h(\widehat{R}(d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(e_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\nonumber\\ \displaystyle & & \displaystyle +\,h(\widehat{R}(d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))\,d\unicode[STIX]{x1D719}(Je_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T))]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 0.\end{eqnarray}$$

Hence we have

(5.4) $$\begin{eqnarray}-\frac{1}{2}\unicode[STIX]{x1D6E5}_{b}|d\unicode[STIX]{x1D719}(T)|^{2}\geqslant 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}.\end{eqnarray}$$

The divergence theorem yields

$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}=0.\end{eqnarray}$$

The fact that $\unicode[STIX]{x1D719}$ is foliated can be easily obtained by Lemma 5.2.◻

The next result gives another proof of Petit’s result.

Theorem 5.2. (cf. [16])

Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is a harmonic map. Then $\unicode[STIX]{x1D719}$ is foliated.

Proof. Since $\unicode[STIX]{x1D719}$ is harmonic, we have $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})=0$ . By (5.2), we get

(5.5) $$\begin{eqnarray}-\frac{1}{2}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}\geqslant 2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}.\end{eqnarray}$$

Using the divergence theorem, we derive $\unicode[STIX]{x1D719}_{00}^{i}=\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}=\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}=0$ . By Lemma 5.2 again, we find that the map $\unicode[STIX]{x1D719}$ is foliated.◻

Remark 5.1. From Theorems 5.1 and 5.2, we get that if $M$ is a compact Sasakian manifold and $N$ is a Riemannian manifold with nonpositive curvature, then the map $\unicode[STIX]{x1D719}:M\rightarrow N$ is harmonic if and only if it is pseudoharmonic.

Now we use a technique in [17] to treat harmonic maps or pseudoharmonic maps from complete noncompact pseudo-Hermitian manifolds. Here the completeness of a pseudo-Hermitian manifold is with respect to the Webster metric. Let $r$ be the Riemannian distance on the complete noncompact pseudo-Hermitian manifold $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ from a fixed point $x_{0}\in M$ . Set $B_{R}=\{x\in M:r(x)<R\}$ .

For a measurable function $u$ defined on $\mathbb{R}$ , we use the notation $u\notin L^{1}(+\infty )$ to mean that $|u|\notin L^{1}((K,+\infty ))$ for any positive number  $K$ .

Proposition 5.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold of dimension $2m+1$ and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

(5.6) $$\begin{eqnarray}\left(\int _{\unicode[STIX]{x2202}B_{r}}|d\unicode[STIX]{x1D719}(T)|^{2}{\mathcal{H}}\right)^{-1}\notin L^{1}(+\infty ),\end{eqnarray}$$

where ${\mathcal{H}}$ is the $2m$ -dimensional Hausdorff measure on $\unicode[STIX]{x2202}B_{r}$ , which coincides with the Riemannian measure induced on the regular part of $\unicode[STIX]{x2202}B_{r}$ , then the second fundamental form satisfies $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$ for any $X\in H(M)$ .

Proof. We consider only the case $\unicode[STIX]{x1D719}$ is a harmonic map, because the other case is analogous. By the divergence theorem, (5.5) gives

(5.7) $$\begin{eqnarray}\displaystyle \int _{B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right)\unicode[STIX]{x1D6F9} & {\leqslant} & \displaystyle -\frac{1}{2}\int _{B_{r}}\unicode[STIX]{x1D6E5}|d\unicode[STIX]{x1D719}(T)|^{2}\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}.\end{eqnarray}$$

Here the quantity $\sum _{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}$ is well-defined, since it is independent of the choice of the local frame fields on $M$ and  $N$ . Recalling $\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2}=2\sum _{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}T_{\bar{\unicode[STIX]{x1D6FC}}}+\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{0\bar{\unicode[STIX]{x1D6FC}}}^{i}T_{\unicode[STIX]{x1D6FC}})+2\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{00}^{i}T$ we have

(5.8) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\int _{\unicode[STIX]{x2202}B_{r}}g_{\unicode[STIX]{x1D703}}\left(\unicode[STIX]{x1D6FB}|d\unicode[STIX]{x1D719}(T)|^{2},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$

Let

$$\begin{eqnarray}\unicode[STIX]{x1D701}(r)=\int _{B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right)\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Then by the co-area formula, we get

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}^{\prime }(r) & = & \displaystyle \frac{d}{dr}\left\{\int _{0}^{r}\int _{\unicode[STIX]{x2202}B_{t}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}\,dt\right\}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x2202}B_{r}}\left(2\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}|^{2}+|\unicode[STIX]{x1D719}_{00}^{i}|^{2}\right){\mathcal{H}}.\nonumber\end{eqnarray}$$

Putting together (5.7) and (5.8) and squaring we finally get

(5.9) $$\begin{eqnarray}\unicode[STIX]{x1D701}(r)^{2}\leqslant \left(\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right)\unicode[STIX]{x1D701}^{\prime }(r).\end{eqnarray}$$

Next, we reason by contradiction and we suppose $\unicode[STIX]{x1D719}_{0\unicode[STIX]{x1D6FC}}^{i}\neq 0$ for some  $\unicode[STIX]{x1D6FC}$ . It follows that there exists a $R>0$ sufficiently large such that $\unicode[STIX]{x1D701}(r)>0$ , for every $r\geqslant R$ . Fix such an  $R$ . From (5.9) we then derive

$$\begin{eqnarray}\unicode[STIX]{x1D701}(R)^{-1}\geqslant \unicode[STIX]{x1D701}(R)^{-1}-\unicode[STIX]{x1D701}(r)^{-1}\geqslant \int _{R}^{r}\frac{dt}{\int _{\unicode[STIX]{x2202}B_{t}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}},\end{eqnarray}$$

and letting $r\rightarrow +\infty$ we contradict (5.6).◻

Corollary 5.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

(5.10) $$\begin{eqnarray}\int _{B_{r}}|d\unicode[STIX]{x1D719}(T)|^{2}\unicode[STIX]{x1D6F9}\leqslant Cr^{2},\end{eqnarray}$$

then the second fundamental form satisfies $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$ for any $X\in H(M)$ .

Proof. Set

$$\begin{eqnarray}h(r)=\int _{B_{r}}|d\unicode[STIX]{x1D719}(T)|^{2}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

So, by the co-area formula, we have

$$\begin{eqnarray}h^{\prime }(r)=\int _{\unicode[STIX]{x2202}B_{r}}|d\unicode[STIX]{x1D719}(T)|^{2}{\mathcal{H}}.\end{eqnarray}$$

From of [18, Proposition 3.1], we know that

$$\begin{eqnarray}\frac{r}{h(r)}\notin L^{1}(+\infty )\quad \text{implies}~\frac{1}{h^{\prime }(r)}\notin L^{1}(+\infty ).\end{eqnarray}$$

Suppose that $\unicode[STIX]{x1D719}$ satisfies (5.10), this implies

$$\begin{eqnarray}\frac{r}{h(r)}\notin L^{1}(+\infty ).\end{eqnarray}$$

Thus we deduce $1/h^{\prime }(r)\notin L^{1}(+\infty )$ , that is, $\unicode[STIX]{x1D719}$ satisfies (5.6). Hence we prove the corollary.◻

Proposition 5.2. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact pseudo-Hermitian manifold and $(N,h)$ a Riemannian manifold. Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be a smooth map. If the second fundamental form satisfies $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})(T,X)=0$ for any $X\in H(M)$ and

(5.11) $$\begin{eqnarray}\left(\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right)^{-1}\notin L^{1}(+\infty ),\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is foliated.

Proof. By the property of $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D719})$ and the divergence theorem, we have

$$\begin{eqnarray}\displaystyle m\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9} & = & \displaystyle -\sqrt{-1}\int _{B_{r}}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FC}}})\unicode[STIX]{x1D6F9}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\nonumber\end{eqnarray}$$

Set $\unicode[STIX]{x1D702}(r)=\int _{B_{r}}|\unicode[STIX]{x1D719}_{0}^{i}|^{2}\unicode[STIX]{x1D6F9}$ . Then we have

$$\begin{eqnarray}\frac{m^{2}}{4}\unicode[STIX]{x1D702}(r)^{2}\leqslant \left(\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right)\unicode[STIX]{x1D702}^{\prime }(r).\end{eqnarray}$$

If $\unicode[STIX]{x1D719}$ is not foliated, then for $r>R$ ,

$$\begin{eqnarray}\unicode[STIX]{x1D702}(R)^{-1}-\unicode[STIX]{x1D702}(r)^{-1}\geqslant \int _{R}^{r}\frac{dt}{\int _{\unicode[STIX]{x2202}B_{t}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}},\end{eqnarray}$$

where $R$ is large enough such that $\unicode[STIX]{x1D702}(R)>0$ , and letting $r\rightarrow +\infty$ we contradict (5.11).◻

Theorem 5.3. Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

(5.12) $$\begin{eqnarray}\left(\int _{\unicode[STIX]{x2202}B_{r}}e(\unicode[STIX]{x1D719}){\mathcal{H}}\right)^{-1}\notin L^{1}(+\infty ),\end{eqnarray}$$

where $e(\unicode[STIX]{x1D719})=(1/2)\text{trace}_{g_{\unicode[STIX]{x1D703}}}(\unicode[STIX]{x1D719}^{\ast }h)$ is the energy density of $\unicode[STIX]{x1D719}$ , then $\unicode[STIX]{x1D719}$ is a foliated map.

Proof. Since $e(\unicode[STIX]{x1D719})=e_{H}(\unicode[STIX]{x1D719})+(1/2)|d\unicode[STIX]{x1D719}(T)|^{2}$ , the condition (5.12) implies both (5.6) and (5.11). It follows from Propositions 5.1 and 5.2 that $\unicode[STIX]{x1D719}$ is foliated.◻

Corollary 5.2. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

(5.13) $$\begin{eqnarray}\int _{B_{r}}e(\unicode[STIX]{x1D719})\unicode[STIX]{x1D6F9}\leqslant Cr^{2},\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is foliated.

6 $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonicity results

In this section, we give some conditions to ensure the $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonicity for both harmonic and pseudoharmonic maps from either a compact Sasakian manifold or a complete Sasakian manifold. Recall that Petit [16] gave similar results for harmonic maps from a compact Sasakian manifold by using tools of spinorial geometry, although he did not mention the notion of $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonicity. The moving frame method, which enables us to treat both cases of harmonic maps and pseudoharmonic maps, seems closer to the classical methods in differential geometry. Let $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$ be a smooth map from a pseudo-Hermitian manifold $M$ into a Riemannian manifold $N$ . Inspired by Sampson’s technique (cf. [6, 19]), we introduce a global 1-form on $M$ given by

(6.1) $$\begin{eqnarray}\unicode[STIX]{x1D703}_{W_{1}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\end{eqnarray}$$

in terms of the local orthonormal admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ on $M$ and the local orthonormal coframe field $\{\unicode[STIX]{x1D70E}^{i}\}$ on  $N$ .

Lemma 6.1.

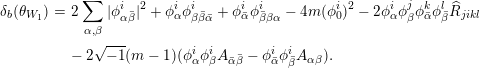(6.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$

Proof. By the definition of the divergence of 1-forms on $M$ , we have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}+(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}),_{\bar{\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{i}.\nonumber\end{eqnarray}$$

Using (3.7), (3.10) and their complex conjugate, we get

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}-2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2m\sqrt{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{j}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{k}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2m\sqrt{-1}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D719}_{0}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}-2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{i}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}-4m(\unicode[STIX]{x1D719}_{0}^{i})^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{i}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{i}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\nonumber\end{eqnarray}$$

Theorem 6.1. Let $(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold of and $(N^{n},h)$ be a Riemannian manifold with nonpositive Hermitian curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. Then $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic and

(6.3) $$\begin{eqnarray}\mathop{\sum }_{i,j,k,l}^{n}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{ijkl}=0,\quad \text{for any}~\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}.\end{eqnarray}$$

Proof. The fact that $N$ has a nonpositive Hermitian curvature implies that the sectional curvature of $N$ is nonpositive. According to Theorems 5.1 and 5.2, we know that the condition that $\unicode[STIX]{x1D719}$ is harmonic is equivalent to that $\unicode[STIX]{x1D719}$ is pseudoharmonic. Besides, we get that the map is foliated in this circumstance. By (3.7), we have $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$ for any $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ . Thus we have $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}E_{i}$ , where $\{E_{i}\}$ is the dual vector field of  $\{\unicode[STIX]{x1D70E}^{i}\}$ .

From (6.2), we get

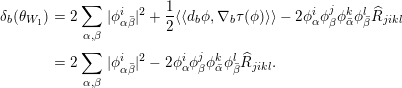(6.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}}) & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\frac{1}{2}\langle \langle d_{b}\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB}_{b}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})\rangle \rangle -2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}-2\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}.\end{eqnarray}$$

Since $N$ has nonpositive Hermitian curvature, we have

(6.5) $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{l}\widehat{R}_{jikl}\leqslant 0\quad \text{for any fixed}~\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}.\end{eqnarray}$$

By the divergence theorem, we derive from (6.4) that $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map with property (6.3).◻

Then consider the case that the target manifold $(N,h)$ is a Kähler manifold. The curvature operator $\widetilde{Q}$ of $N$ is defined by

$$\begin{eqnarray}\langle \widetilde{Q}(X\wedge Y),Z\wedge W\rangle =\langle \widetilde{R}(X,Y)W,Z\rangle\end{eqnarray}$$

for any $X,Y,Z,W\in T(N)$ . The complex extension of $\widetilde{Q}$ to $\wedge ^{2}T^{\mathbb{C}}(N)$ is also denoted by $\widetilde{Q}$ . Let us set

$$\begin{eqnarray}\langle \!\langle \widetilde{Q}(X\wedge Y),Z\wedge W\rangle \!\rangle =\langle \widetilde{Q}(X\wedge Y),\overline{Z\wedge W}\rangle .\end{eqnarray}$$

The Kähler identity of $N$ yields

$$\begin{eqnarray}\widetilde{Q}|_{\wedge ^{(2,0)}T^{\mathbb{C}}(N)}=\widetilde{Q}|_{\wedge ^{(0,2)}T^{\mathbb{C}}(N)}=0.\end{eqnarray}$$

Set

$$\begin{eqnarray}\widetilde{Q}^{(1,1)}=\widetilde{Q}:\wedge ^{(1,1)}T^{\mathbb{C}}(N)\rightarrow \wedge ^{(1,1)}T^{\mathbb{C}}(N).\end{eqnarray}$$

Definition 6.1. (cf. [20])

Let $(N,h)$ be a Kähler manifold. The curvature tensor of $N$ is said to be strongly negative (resp. strongly seminegative) if

$$\begin{eqnarray}\langle \!\langle \widetilde{Q}^{(1,1)}(\unicode[STIX]{x1D709}),\unicode[STIX]{x1D709}\rangle \!\rangle =\langle \widetilde{Q}^{(1,1)}(\unicode[STIX]{x1D709}),\overline{\unicode[STIX]{x1D709}}\rangle <0\quad (\text{resp.}~\leqslant 0)\end{eqnarray}$$

for any $\unicode[STIX]{x1D709}=(Z\wedge W)^{(1,1)}\neq 0$ , $Z,W\in \unicode[STIX]{x1D6E4}^{\infty }(T^{\mathbb{C}}(N))$ .

Let $\unicode[STIX]{x1D719}:(M^{2m+1},T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N^{n},h)$ be a smooth map from a pseudo-Hermitian manifold $M$ into a Kähler manifold  $N$ . Similar to (6.1) (cf. [19] and [6]), we introduce a global 1-form on $M$ defined as

(6.6) $$\begin{eqnarray}\unicode[STIX]{x1D703}_{W_{2}}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\unicode[STIX]{x1D703}^{\bar{\unicode[STIX]{x1D6FD}}},\end{eqnarray}$$

in terms of the local orthonormal admissible coframe $\{\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D6FC}}\}$ on $M$ and the local orthonormal frame field $\{\widetilde{E}_{i}\}$ on  $N$ . By (3.7), (3.23) and their complex conjugate, we have

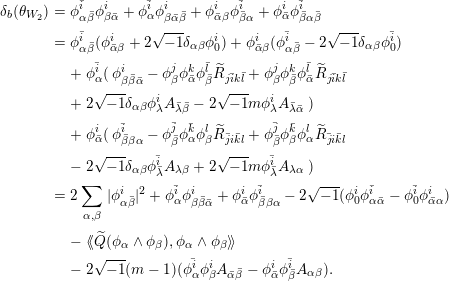(6.7) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{2}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{\bar{i}}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}(\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}+2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{i})+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}-2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{0}^{\bar{i}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\! (\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{j}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{k}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{\bar{l}}\widetilde{R}_{j\bar{i}k\bar{l}}\nonumber\\ \displaystyle & & \displaystyle +\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FD}}}-2\sqrt{-1}m\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}^{i}A_{\bar{\unicode[STIX]{x1D706}}\bar{\unicode[STIX]{x1D6FC}}} )\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\! (\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{j}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{\bar{k}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{l}\widetilde{R}_{\bar{j}i\bar{k}l}\nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}}+2\sqrt{-1}m\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D706}}}^{\bar{i}}A_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}})\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}\bar{\unicode[STIX]{x1D6FC}}}^{i}+\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}^{\bar{i}}-2\sqrt{-1}(\unicode[STIX]{x1D719}_{0}^{i}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FC}}}^{\bar{i}}-\unicode[STIX]{x1D719}_{0}^{\bar{i}}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}}^{i})\nonumber\\ \displaystyle & & \displaystyle -\,\langle \!\langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \!\rangle \nonumber\\ \displaystyle & & \displaystyle -\,2\sqrt{-1}(m-1)(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}^{\bar{i}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}^{i}A_{\bar{\unicode[STIX]{x1D6FC}}\bar{\unicode[STIX]{x1D6FD}}}-\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}}^{i}\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}A_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$

Theorem 6.2. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ be a harmonic or pseudoharmonic map from a compact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. Then $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map and

(6.8) $$\begin{eqnarray}\langle \langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \rangle =0,\quad \text{for any}~\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\end{eqnarray}$$

where $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}=d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}})$ .

Proof. Since strongly seminegative curvature implies nonpositive sectional curvature, we get that $\unicode[STIX]{x1D719}$ must be pseudoharmonic and foliated. Then we have $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$ and $\unicode[STIX]{x1D719}_{0}^{i}=0$ . So we get $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D719})=2(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}\widetilde{E}_{i}+\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}\widetilde{E}_{\bar{i}})=0$ , that is, $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}\bar{\unicode[STIX]{x1D6FD}}}^{\bar{i}}=0$ . As $M$ is Sasakian, by (6.7) we have

(6.9) $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{2}})=2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}-\langle \!\langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \!\rangle .\end{eqnarray}$$

The divergence theorem and the curvature condition of $N$ imply that $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic and $\langle \langle \widetilde{Q}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}),\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\wedge \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}\rangle \rangle =0$ , for any $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ .◻

Now we attempt to give some conditions to ensure $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonicity for harmonic and pseudoharmonic maps from complete noncompact Sasakian manifolds.

Theorem 6.3. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive Hermitian curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

(6.10) $$\begin{eqnarray}\left(\int _{\unicode[STIX]{x2202}B_{r}}e(\unicode[STIX]{x1D719}){\mathcal{H}}\right)^{-1}\notin L^{1}(+\infty ),\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map with the property (6.3).

Proof. By Theorem 5.3, we get that $\unicode[STIX]{x1D719}$ is foliated and pseudoharmonic. From (6.4) and (6.5), we have

$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{1}})\geqslant 2\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}.\end{eqnarray}$$

Using the divergence theorem, we get

(6.11) $$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{1}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\geqslant 2\int _{B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

On the other hand, by the definition of $\unicode[STIX]{x1D703}_{W_{1}}$ , we have

(6.12) $$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{1}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$

Putting together (6.11) and (6.12) and squaring we finally get

(6.13) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}(r)^{2}\leqslant \left(\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right)\unicode[STIX]{x1D6FE}^{\prime }(r),\end{eqnarray}$$

where we have set

$$\begin{eqnarray}\unicode[STIX]{x1D6FE}(r)=\int _{B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Next suppose that $\unicode[STIX]{x1D719}$ is not $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic. Then there exists a $R>0$ sufficiently large such that $\unicode[STIX]{x1D6FE}(R)>0$ . For any $r\geqslant R$ , from (6.13) we can deduce

$$\begin{eqnarray}\unicode[STIX]{x1D6FE}(R)^{-1}-\unicode[STIX]{x1D6FE}(r)^{-1}\geqslant \int _{R}^{r}\frac{dt}{\int _{\unicode[STIX]{x2202}B_{t}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}},\end{eqnarray}$$

and letting $r\rightarrow +\infty$ we contradict (6.10). Hence $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic and $\unicode[STIX]{x1D703}_{W_{1}}\equiv 0$ . Then (6.2) implies that $\unicode[STIX]{x1D719}$ satisfies (6.3).◻

Corollary 6.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a complete noncompact Sasakian manifold and $(N,h)$ be a Riemannian manifold with nonpositive Hermitian curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map. If $\unicode[STIX]{x1D719}$ satisfies

$$\begin{eqnarray}\int _{B_{r}}e(\unicode[STIX]{x1D719})\unicode[STIX]{x1D6F9}\leqslant Cr^{2},\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map with the property (6.3).

Theorem 6.4. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If $\unicode[STIX]{x1D719}$ satisfies

(6.14) $$\begin{eqnarray}\left(\int _{\unicode[STIX]{x2202}B_{r}}e(\unicode[STIX]{x1D719}){\mathcal{H}}\right)^{-1}\notin L^{1}(+\infty ),\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map with the property (6.8).

Proof. Obviously, the map $\unicode[STIX]{x1D719}$ is foliated, and hence $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}=\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}}^{i}$ . It follows from (6.7) that

$$\begin{eqnarray}2\int _{B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}\bar{\unicode[STIX]{x1D6FD}}}^{i}|^{2}\unicode[STIX]{x1D6F9}\leqslant \int _{B_{r}}\unicode[STIX]{x1D6FF}_{b}(\unicode[STIX]{x1D703}_{W_{2}})\unicode[STIX]{x1D6F9}=\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{2}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}.\end{eqnarray}$$

By the definition of $\unicode[STIX]{x1D703}_{W_{2}}$ , we have

$$\begin{eqnarray}\int _{\unicode[STIX]{x2202}B_{r}}\unicode[STIX]{x1D703}_{W_{2}}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\right){\mathcal{H}}\leqslant 2\left\{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right\}^{1/2}\left\{\int _{\unicode[STIX]{x2202}B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}|^{2}{\mathcal{H}}\right\}^{1/2}.\end{eqnarray}$$

Set

$$\begin{eqnarray}\unicode[STIX]{x1D70C}(r)=\int _{B_{r}}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}|\unicode[STIX]{x1D719}_{\bar{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FD}}^{i}|^{2}\unicode[STIX]{x1D6F9}.\end{eqnarray}$$

Then

(6.15) $$\begin{eqnarray}\unicode[STIX]{x1D70C}(r)^{2}\leqslant \unicode[STIX]{x1D70C}^{\prime }(r)\left(\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}\right).\end{eqnarray}$$

Suppose that $\unicode[STIX]{x1D719}$ is not $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic, then there exists a $R>0$ sufficiently large such that $\unicode[STIX]{x1D70C}(r)>0$ for any $r>R$ . Fix such a $R$ . From (6.15) we deduce the following

$$\begin{eqnarray}\unicode[STIX]{x1D70C}(R)^{-1}-\unicode[STIX]{x1D70C}(r)^{-1}\geqslant \int _{R}^{r}\frac{dt}{\int _{\unicode[STIX]{x2202}B_{r}}e_{H}(\unicode[STIX]{x1D719}){\mathcal{H}}},\end{eqnarray}$$

and letting $r\rightarrow +\infty$ we contradict (6.14). Hence $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic and $\unicode[STIX]{x1D703}_{W_{2}}\equiv 0$ . Then (6.7) implies that $\unicode[STIX]{x1D719}$ satisfies (6.8).◻

Corollary 6.2. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ be a harmonic or pseudoharmonic map from a complete noncompact Sasakian manifold into a Kähler manifold with strongly seminegative curvature. If $\unicode[STIX]{x1D719}$ satisfies

$$\begin{eqnarray}\int _{B_{r}}e(\unicode[STIX]{x1D719})\unicode[STIX]{x1D6F9}\leqslant Cr^{2},\end{eqnarray}$$

then $\unicode[STIX]{x1D719}$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map with the property (6.8).

7 Siu–Sampson type results

In this section, we establish some results of Siu–Sampson type for both harmonic maps and pseudoharmonic maps from compact Sasakian manifolds. Similar to the results for harmonic maps from Kähler manifolds in [3, 19, 20], we may derive $(J,J^{N})$ -holomorphicity under rank conditions for harmonic and pseudoharmonic maps from compact Sasakian manifolds by analysing the curvature equations (6.8). Note that Petit [16] also gave the $(J,J^{N})$ -holomorphicity results for harmonic maps from Sasakian manifolds using spinorial geometry. As mentioned previously, our method is different from his. Besides recapturing Petit’s results by using the moving frame method, we also add some new results which include the results for pseudoharmonic maps, the conic extension of harmonic maps from Sasakian manifolds and a unique continuation theorem for $(J,J^{N})$ -holomorphicity.

First, we consider the case where the target manifold $N$ is a locally symmetric space of noncompact type (cf. [3, 19]). The universal covering manifold of $N$ is a symmetric space $G/K$ , where $K$ is a connected and closed subgroup of the noncompact connected Lie group $G$ , and $G/K$ is given the invariant metric determined by the Killing form $\langle ,\rangle$ on  $\mathfrak{g}$ . If the corresponding Cartan decomposition of the Lie algebra of $G$ is $\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$ , then the real tangent space of $N$ at any point can be identified with  $\mathfrak{p}$ . The Killing form $\langle ,\rangle$ is positive definite on $\mathfrak{p}$ and negative definite on $\mathfrak{k}$ . The curvature tensor of $N$ is given by

$$\begin{eqnarray}\widehat{R}(X,Y)Z=-[[X,Y],Z],\end{eqnarray}$$

for any $X,Y,Z\in \mathfrak{p}$ , and the Hermitian curvature of $N$ is given by

(7.1) $$\begin{eqnarray}\langle \widehat{R}(\overline{X},\overline{Y})Y,X\rangle =\langle [X,Y],[\overline{X},\overline{Y}]\rangle ,\end{eqnarray}$$

which is nonpositive, and zero if and only if $[X,Y]=0$ , because of $[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$ . By Theorem 6.1, we get

(7.2) $$\begin{eqnarray}[d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FC}}),d\unicode[STIX]{x1D719}(T_{\unicode[STIX]{x1D6FD}})]=0,\end{eqnarray}$$

for any $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ . Thus we have

Proposition 7.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold and $N$ a locally symmetric space of noncompact type. If $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map, then $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic and for any $x\in M$ , $d\unicode[STIX]{x1D719}_{x}$ maps $T_{1,0}(M)_{x}$ onto an abelian subspace $W$ of $\mathfrak{p}\otimes \mathbb{C}$ .

Under the assumption of Proposition 7.1, the image under $d\unicode[STIX]{x1D719}_{x}$ of real tangent space $T_{x}(M)$ is the subspace of real points of space $W+\overline{W}\subset T_{\unicode[STIX]{x1D719}(x)}^{\mathbb{C}}(N)$ , so that

$$\begin{eqnarray}\dim _{\mathbb{R}}\,d\unicode[STIX]{x1D719}_{x}(T_{x}(M))=\dim _{\mathbb{C}}(W+\overline{W})\leqslant 2\dim _{\mathbb{C}}W.\end{eqnarray}$$

If $G/K$ is a Hermitian symmetric space, then corresponding to any invariant complex structure on $G/K$ we have the decomposition

$$\begin{eqnarray}\mathfrak{p}\otimes \mathbb{C}=\mathfrak{p}^{1,0}\oplus \mathfrak{p}^{0,1},\end{eqnarray}$$

and the integrability condition $[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]\subset \mathfrak{p}^{1,0}$ is equivalent, in view of $[\mathfrak{p},\mathfrak{p}]\subset \mathfrak{k}$ , to $[\mathfrak{p}^{1,0},\mathfrak{p}^{1,0}]=0$ , thus $\mathfrak{p}^{1,0}$ is an abelian subalgebra of $\mathfrak{p}\otimes \mathbb{C}$ .

Lemma 7.1. (cf. [3])

Let $G/K$ be a symmetric space of noncompact type. Let $W\subset \mathfrak{p}\otimes \mathbb{C}$ be an abelian subspace. Then $\dim W\leqslant (1/2)\dim \mathfrak{p}\otimes \mathbb{C}$ . Equality holds in this inequality if and only if $G/K$ is Hermitian symmetric and $W=\mathfrak{p}^{1,0}$ for an invariant complex structure on $G/K$ .

From Lemma 7.1, we get immediately the following result.

Corollary 7.1. Let $\unicode[STIX]{x1D719}:M\rightarrow N$ be as in Proposition 7.1 and suppose that $N$ is not locally Hermitian symmetric. Then $\text{rank}\,d\unicode[STIX]{x1D719}<\dim N$ .

The above corollary use only the case of strict inequality in Lemma 7.1. We have treated the case of equality in such detail in order to obtain the following theorem.

Theorem 7.1. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold and $N$ a locally Hermitian symmetric space of noncompact type whose universal cover does not contain the hyperbolic plane as a factor. If $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map, and there is a point $x\in M$ such that $d\unicode[STIX]{x1D719}(T_{x}(M))=T_{\unicode[STIX]{x1D719}(x)}(N)$ , then $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic.

Proof. Since $d\unicode[STIX]{x1D719}(T_{1,0}(M))$ is an abelian subspace of half the dimension, it must be $\mathfrak{p}^{1,0}$ for an invariant complex structure on $N$ , that is, $d\unicode[STIX]{x1D719}_{x}(T_{1,0}(M)_{x})=\mathfrak{p}^{1,0}$ . Consequently this property must hold on a neighborhood $U$ of  $x$ . By Proposition 7.1 and Proposition 2.2, we have $d\unicode[STIX]{x1D719}(T)=0$ . Therefore, the map $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic on  $U$ . We get that the map $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic on $M$ by the following unique continuation Proposition 7.2.◻

Then, we give some fundamental knowledge about the warped product. Let $(B,g_{B})$ and $(S,g_{S})$ be two Riemannian manifolds and $f$ be a positive smooth function on  $B$ . Consider the product manifold $B\times S$ with its natural projections $\unicode[STIX]{x1D70B}_{B}:B\times S\rightarrow B$ and $\unicode[STIX]{x1D70B}_{S}:B\times S\rightarrow S$ . The warped product $B\times _{f}S$ is the manifold $B\times S$ furnished with the following Riemannian metric

(7.3) $$\begin{eqnarray}\widetilde{g}=\unicode[STIX]{x1D70B}_{B}^{\ast }(g_{B})+(f\circ \unicode[STIX]{x1D70B}_{B})^{2}\unicode[STIX]{x1D70B}_{S}^{\ast }(g_{S}).\end{eqnarray}$$

The Levi-Civita connection of $B\times _{f}S$ can now be related to those of $B$ and $S$ as follows.

Lemma 7.2. (cf. [15, p. 206])

Let $\widetilde{\unicode[STIX]{x1D6FB}}$ , $^{B}\unicode[STIX]{x1D6FB}$ and $^{S}\unicode[STIX]{x1D6FB}$ be the Levi-Civita connections on $B\times _{f}S$ , $B$ and $S$ respectively. If $V$ , $W$ are vector fields on $B$ , and $X$ , $Y$ are vector fields on $S$ , the lift of $X,Y,V,W$ to $B\times _{f}S$ are also denoted by the same notations, then

1. (i) $\widetilde{\unicode[STIX]{x1D6FB}}_{V}W$ is the lift of $^{B}\unicode[STIX]{x1D6FB}_{V}W$ ;

2. (ii) $\widetilde{\unicode[STIX]{x1D6FB}}_{V}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}V=(Vf/f)X$ ;

3. (iii) $(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{B}=-(\tilde{g}(X,Y)/f)\,\text{grad}\,f$ ;

4. (iv) $(\widetilde{\unicode[STIX]{x1D6FB}}_{X}Y)_{S}$ is the lift of $^{S}\unicode[STIX]{x1D6FB}_{X}Y$ on  $S$ .

We consider the special case: let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold and $C(M)$ be the manifold $\mathbb{R}^{+}\times _{r}M$ endowed with the metric $\widetilde{g}=dr^{2}+r^{2}g_{\unicode[STIX]{x1D703}}$ . Therefore, by Lemma 7.2, we have

(7.4) $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=0,\qquad \widetilde{\unicode[STIX]{x1D6FB}}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r}X=\widetilde{\unicode[STIX]{x1D6FB}}_{X}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}=\frac{1}{r}X,\\ \displaystyle \widetilde{\unicode[STIX]{x1D6FB}}_{X}Y=\unicode[STIX]{x1D6FB}_{X}^{\unicode[STIX]{x1D703}}Y-rg_{\unicode[STIX]{x1D703}}(X,Y)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}.\end{array}\end{eqnarray}$$

Theorem 7.2. (cf. [2])

If $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ is a Sasakian manifold, then $(C(M),\tilde{g})$ is Kähler.

Proof. Set $\unicode[STIX]{x1D701}=r(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)$ and define smooth section of $\text{End}\,TC(M)$ by the formula

(7.5) $$\begin{eqnarray}\widetilde{J}Y=JY-\unicode[STIX]{x1D703}(Y)\unicode[STIX]{x1D701},\qquad \widetilde{J}\unicode[STIX]{x1D701}=T.\end{eqnarray}$$

It is easy to see that $\widetilde{J}$ is an almost complex structure on $C(M)$ and the metric $\widetilde{g}$ is Hermitian. From (7.4) and (7.5) we can show that $\widetilde{\unicode[STIX]{x1D6FB}}\widetilde{J}=0$ . Thus $C(M)$ is Kähler.◻

Lemma 7.3. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a pseudo-Hermitian manifold, $(C(M),\widetilde{g})$ its cone manifold, $(N^{n},h)$ a Riemannian manifold. If $\unicode[STIX]{x1D719}:M\rightarrow N$ is a harmonic map, then the conic extension $\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$ defined by

(7.6) $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D719}}(x,r)=\unicode[STIX]{x1D719}(x)\end{eqnarray}$$

is also harmonic.

Proof. We take a local orthonormal frame field $\{T,e_{\unicode[STIX]{x1D6FC}},Je_{\unicode[STIX]{x1D6FC}}\}$ on $T(M)$ , then $\{(1/r)T,(1/r)e_{\unicode[STIX]{x1D6FC}},(1/r)Je_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}$ is an orthonormal local frame field on $T(C(M))$ . By (7.4), we get that the usual tension field of $\widetilde{\unicode[STIX]{x1D719}}$ is equivalent to $(1/r^{2})\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719})$ . Thus, the harmonicity of $\widetilde{\unicode[STIX]{x1D719}}$ follows that of  $\unicode[STIX]{x1D719}$ .◻

Lemma 7.4. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h,J^{N})$ be a smooth map from a Sasakian manifold to a Kähler manifold, $(C(M),\widetilde{g})$ the cone manifold of  $M$ . Then:

1. (i) $\unicode[STIX]{x1D719}$ is a $(J,J^{N})$ -holomorphic (resp. anti- $(J,J^{N})$ -holomorphic) map if and only if the conic extension $\widetilde{\unicode[STIX]{x1D719}}$ is holomorphic (resp. antiholomorphic);

2. (ii) if $\unicode[STIX]{x1D719}:M\rightarrow N$ is a $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map, then the conic extension $\widetilde{\unicode[STIX]{x1D719}}$ is a pluriharmonic map.

Proof. (i) It can be proved by (7.5). We omit the details.

(ii) If $\unicode[STIX]{x1D719}$ is $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic, then by Proposition 2.2 we have $d\unicode[STIX]{x1D719}(T)=0$ . Let $B(\widetilde{\unicode[STIX]{x1D719}})$ be the usual second fundamental form for $\widetilde{\unicode[STIX]{x1D719}}$ . From (7.5), (7.4) and (2.4) we get

$$\begin{eqnarray}B(\widetilde{\unicode[STIX]{x1D719}})(\widetilde{X},\widetilde{Y})+B(\widetilde{\unicode[STIX]{x1D719}})(\widetilde{J}\widetilde{X},\widetilde{J}\widetilde{Y})=0,\end{eqnarray}$$

for any $\widetilde{X},\widetilde{Y}\in T(C(M))$ . Therefore, the map $\widetilde{\unicode[STIX]{x1D719}}$ is pluriharmonic.◻

In [20], Siu derived the following unique continuation theorem for holomorphicity.

Lemma 7.5. (cf. [20])

Suppose $M,N$ are two Kähler manifolds ( $M$ is connected) and $\unicode[STIX]{x1D719}:M\rightarrow N$ is a harmonic map. Let $U$ be a nonempty open subset of  $M$ . If $\unicode[STIX]{x1D719}$ is holomorphic (resp. antiholomorphic) on  $U$ , then $\unicode[STIX]{x1D719}$ is holomorphic (resp. antiholomorphic) on  $M$ .

From the Lemmas 7.3–7.5, we get the following unique continuation theorem.

Proposition 7.2. Let $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ be a harmonic map from a connected Sasakian manifold to a Kähler manifold. Let $U$ be a nonempty open subset of  $M$ . If $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic (resp. anti- $(J,J^{N})$ -holomorphic) on $U$ , then $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic (resp. anti- $(J,J^{N})$ -holomorphic) on  $M$ .

Proof. From Lemma 7.3, we get that $\widetilde{\unicode[STIX]{x1D719}}:C(M)\rightarrow N$ is harmonic. Suppose $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic on $U$ . It follows from Lemma 7.4 that $\widetilde{\unicode[STIX]{x1D719}}$ is holomorphic on $\mathbb{R}_{+}\times _{r}U$ . By Lemma 7.5, we have that $\widetilde{\unicode[STIX]{x1D719}}$ is holomorphic on $C(M)$ and thus, from Lemma 7.4, $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic on  $M$ .◻

Now we may establish the following Siu type results.

Theorem 7.3. Let $(M,T_{1,0}(M),\unicode[STIX]{x1D703})$ be a compact Sasakian manifold and $N$ be a Kähler manifold with strongly negative curvature. Suppose $\unicode[STIX]{x1D719}:M\rightarrow N$ is either a harmonic map or a pseudoharmonic map, and $\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 3$ at some point of  $M$ , then $\unicode[STIX]{x1D719}$ is $(J,J^{N})$ -holomorphic or anti- $(J,J^{N})$ -holomorphic on  $M$ .

Proof. From Theorem 6.2 and Lemma 7.3, we know that $\widetilde{\unicode[STIX]{x1D719}}$ is harmonic. By Siu’s results, we have $\widetilde{\unicode[STIX]{x1D719}}$ is $\pm$ holomorphic on $C(M)$ . By Lemma 7.4, we conclude that $\unicode[STIX]{x1D719}$ is $\pm (J,J^{N})$ -holomorphic on  $M$ .◻

Keeping in mind Udagawa’s proof to Theorem 4 of [24] the following result is relevant.

Theorem 7.4. Every $\bar{\unicode[STIX]{x2202}}_{b}$ -pluriharmonic map $\unicode[STIX]{x1D719}:(M,T_{1,0}(M),\unicode[STIX]{x1D703})\rightarrow (N,h)$ from a Sasakian manifold $M$ into an irreducible Hermitian symmetric space $N$ of compact or noncompact type is $\pm (J,J^{N})$ holomorphic if $\text{Max}_{M}\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$ , where $P(N)$ is the degree of strong nondegenerate of the bisectional curvature of $N$ (cf. [21] for the definition of the degree of strong nondegenerate of the bisectional curvature of  $N$ ).

Proof. By Lemma 7.4, we get that $\widetilde{\unicode[STIX]{x1D719}}$ is pluriharmonic. Since $\text{Max}_{M}\,\text{rank}_{\mathbb{R}}\,d\unicode[STIX]{x1D719}\geqslant 2P(N)+1$ implies that $\text{Max}_{C(M)}\text{rank}_{\mathbb{R}}\,d\widetilde{\unicode[STIX]{x1D719}}\geqslant 2P(N)+1$ , it follows from [24, Theorem 4] that $\widetilde{\unicode[STIX]{x1D719}}$ is $\pm$ holomorphic. From Lemma 7.4, we have that $\unicode[STIX]{x1D719}$ is $\pm (J,J^{N})$ -holomorphic.◻