Article contents
On Extensions of Triads
Published online by Cambridge University Press: 22 January 2016
Extract
As an extension of a result due to W. D. Barcus and J. P. Meyer [4], T. Ganea [8] has recently proved a theorem concerning the fibre of the extension E∪CF→B of a fibre map p: E→B to the cone CF erected over the fibre F. In this paper we shall establish a generalized Ganea theorem which asserts that the homotopy type of the fibre of a canonical extension ξ′ of a triad 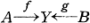 (cf. [13]) is determined by those of f and g (see Theorem 3.4).
(cf. [13]) is determined by those of f and g (see Theorem 3.4).
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1966
References
- 8
- Cited by


