Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harada, Koichiro
1970.
A Characterization of the Simple Group U3(5).
Nagoya Mathematical Journal,
Vol. 38,
Issue. ,
p.
27.
Iwasaki, Shiro
and
Kimura, Hiroshi
1970.
On Some Doubly Transitive Permutation Groups of Degree N And Order 6n(n – 1).
Nagoya Mathematical Journal,
Vol. 37,
Issue. ,
p.
25.
Harada, Koichiro
1971.
On some doubly transitive groups.
Journal of Algebra,
Vol. 17,
Issue. 3,
p.
437.
Hering, Christoph
Kantor, William M.
and
Seitz, Gary M.
1972.
Finite groups with a split BN-pair of rank 1. I.
Journal of Algebra,
Vol. 20,
Issue. 3,
p.
435.
Kantor, William M
O'Nan, Michael E
and
Seitz, Gary M
1972.
2-Transitive groups in which the stabilizer of two points is cyclic.
Journal of Algebra,
Vol. 21,
Issue. 1,
p.
17.
Chunikhin, S. A.
and
Shemetkov, L. A.
1973.
Finite groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 3,
p.
291.
Kimura, Hiroshi
1975.
A characterization of simple groups A6 and A7.
Journal of Algebra,
Vol. 33,
Issue. 2,
p.
161.
Smith, Margaret S
1976.
A combinatorial configuration associated with the Higman-Sims simple group.
Journal of Algebra,
Vol. 41,
Issue. 1,
p.
175.
McDermott, John P. J.
1977.
Transitive permutation groups with 2-point stabilisers of order 2.
Mathematische Zeitschrift,
Vol. 157,
Issue. 1,
p.
37.
Isbell, John
1986.
A class of doubly regular polyhedral surfaces.
Journal of Pure and Applied Algebra,
Vol. 43,
Issue. 1,
p.
89.
Liebeck, Martin W.
and
Praeger, Cheryl E.
2025.
Maps, simple groups, and arc-transitive graphs.
Advances in Mathematics,
Vol. 462,
Issue. ,
p.
110086.


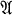
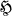 be the normalizer of a Sylow 5-subgroup of
be the normalizer of a Sylow 5-subgroup of 