Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ein, Lawrence
Eisenbud, David
and
Katz, Sheldon
1988.
Algebraic Geometry Sundance 1986.
Vol. 1311,
Issue. ,
p.
51.
Giuffrida, Salvatore
1989.
The Hilbert function of curves on certain smooth quartic surfaces.
Manuscripta Mathematica,
Vol. 65,
Issue. 4,
p.
395.
Ciliberto, Ciro
and
Sernesi, Edoardo
1989.
Curves on surfaces of degree2r-σ in P’.
Commentarii Mathematici Helvetici,
Vol. 64,
Issue. 1,
p.
300.
Ciliberto, Ciro
and
Lopez, Angelo Felice
1991.
On the existence of components of the Noether-Lefschetz locus with given codimension.
Manuscripta Mathematica,
Vol. 73,
Issue. 1,
p.
341.
Giuffrida, Salvatore
and
Maggioni, Renato
1991.
Generators for the ideal of an integral curve lying on a smooth quartic surface.
Journal of Pure and Applied Algebra,
Vol. 76,
Issue. 3,
p.
317.
Floystad, Gunnar
1991.
On space curves with good cohomological properties.
Mathematische Annalen,
Vol. 291,
Issue. 1,
p.
505.
Huybrechts, Daniel
1997.
Birational symplectic manifolds and their deformations.
Journal of Differential Geometry,
Vol. 45,
Issue. 3,
Farkas, G.
2001.
Brill-Noether loci and the gonality stratification of {M_g}.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2001,
Issue. 539,
Johnsen, Trygve
and
Knutsen, Andreas Leopold
2003.
Rational Curves in Calabi-Yau Threefolds.
Communications in Algebra,
Vol. 31,
Issue. 8,
p.
3917.
Brevik, John
2007.
Curves on normal rational cubic surfaces.
Pacific Journal of Mathematics,
Vol. 230,
Issue. 1,
p.
73.
Colombo, Elisabetta
and
Frediani, Paola
2010.
On the second Gaussian map for curves on a K3 surface.
Nagoya Mathematical Journal,
Vol. 199,
Issue. ,
p.
123.
Colombo, Elisabetta
and
Frediani, Paola
2010.
On the second Gaussian map for curves on a K3 surface.
Nagoya Mathematical Journal,
Vol. 199,
Issue. ,
p.
123.
Kaloghiros, Anne-Sophie
2012.
A classification of terminal quartic 3-folds and applications to rationality questions.
Mathematische Annalen,
Vol. 354,
Issue. 1,
p.
263.
Kleppe, Jan O.
and
Ottem, John C.
2015.
Components of the Hilbert scheme of space curves on low-degree smooth surfaces.
International Journal of Mathematics,
Vol. 26,
Issue. 02,
p.
1550017.
Lin, Hai
Wu, Baosen
and
Yau, Shing-Tung
2016.
Heterotic String Compactification and New Vector Bundles.
Communications in Mathematical Physics,
Vol. 345,
Issue. 2,
p.
457.
Degtyarev, Alex
Itenberg, Ilia
and
Sertöz, Ali Sinan
2017.
Lines on quartic surfaces.
Mathematische Annalen,
Vol. 368,
Issue. 1-2,
p.
753.
Nasu, Hirokazu
2017.
Obstructions to deforming curves on a 3-fold, III: Deformations of curves lying on a K3 surface.
International Journal of Mathematics,
Vol. 28,
Issue. 13,
p.
1750099.
Anghel, Cristian
Coandă, Iustin
and
Manolache, Nicolae
2021.
A property of five lines in ℙ3 and four generated 4-instantons.
Communications in Algebra,
Vol. 49,
Issue. 1,
p.
1.
Sierra, José Carlos
2021.
On morphisms from ℙ 3 to 𝔾(1,3).
Comptes Rendus. Mathématique,
Vol. 359,
Issue. 7,
p.
853.
Lelli-Chiesa, Margherita
2022.
A codimension 2 component of the Gieseker-Petri locus.
Journal of Algebraic Geometry,
Vol. 31,
Issue. 4,
p.
751.


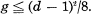 Here we consider curves on smooth quartic surfaces.
Here we consider curves on smooth quartic surfaces.