Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-03T08:54:01.442Z Has data issue: false hasContentIssue false
  • English
  • Français

On Crossed Products of a Sfield

Published online by Cambridge University Press:  22 January 2016

Masatoshi Ikeda
Masatoshi Ikeda*
Affiliation:
Ege University, Bornova-Izmir, Turkey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the previous paper [3] the author has shown a possibility to construct a series of sfields by taking sfields of quotients of split crossed products of a sfield. In this paper the same problem is treated, and, by considering general crossed products, a generalization of the previous result is given: Let K be a sfield and G be the join of a well-ordered ascending chain of groups Gα of outer automorphisms of K such that a) G1 is the identity automorphism group, b) Gα is a group extension of Gα-1 by a torsion-free abelian group for each non-limit ordinal α, and c) 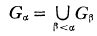for each limit ordinal α. Then an arbitrary crossed product of K with G is an integral domain with a sfield of quotients Q and the commutor ring of K in Q coincides with the centre of K.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 22 , June 1963 , pp. 65 - 71
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1963

References

[1] Asano, K.: Über die Quotientenbildung von Schiefringen, J. Math. Soc. Jap. 1 (1949).CrossRefGoogle Scholar
[2] Azumaya, G. and Nakayama, T.: Daisu-gaku II (Algebras II, in Japanese) Iwanami-shoten (1954).Google Scholar
[3] Ikeda, M.: Schiefkörper unendlichen Ranges über dem Zentrum (forthcoming in Osaka Math. J).Google Scholar
[4] Kurosch, A. G.: Gruppentheorie, Akademie Verlag (1955).Google Scholar