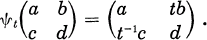Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Loos, Ottmar
1978.
Homogeneous algebraic varieties defined by Jordan pairs.
Monatshefte f�r Mathematik,
Vol. 86,
Issue. 2,
p.
107.
Meyberg, Kurt
1984.
Track formulas and derivations in simple jordan pairs.
Communications in Algebra,
Vol. 12,
Issue. 11,
p.
1311.
Loos, Ottmar
1985.
Charakterisierung symmetrischerR-R�ume durch ihre Einheitsgitter.
Mathematische Zeitschrift,
Vol. 189,
Issue. 2,
p.
211.
Neher, Erhard
1985.
On the classification of lie and jordan triple systems.
Communications in Algebra,
Vol. 13,
Issue. 12,
p.
2615.
KANEYUKI, Soji
1987.
On orbit structure of compactifications of parahermitian symmetric spaces.
Japanese journal of mathematics. New series,
Vol. 13,
Issue. 2,
p.
333.
Dorfmeister, Josef
1993.
Groups associated with a Grassmannian modelled on the Wiener algebra.
Integral Equations and Operator Theory,
Vol. 17,
Issue. 4,
p.
464.
Gradl, H.
1993.
Realization of semisimple lie algebras with polynomial and rational vector fields.
Communications in Algebra,
Vol. 21,
Issue. 11,
p.
4065.
Loos, Ottmar
1995.
Elementary groups and stability for Jordan pairs.
K-Theory,
Vol. 9,
Issue. 1,
p.
77.
Ikai, Hisatoshi
1998.
Some prehomogeneous representations defined by cubic forms.
Tohoku Mathematical Journal,
Vol. 50,
Issue. 3,
Bertram, Wolfgang
2002.
Generalized projective geometries: general theory and equivalence with Jordan structures.
advg,
Vol. 2,
Issue. 4,
p.
329.
Faulkner, John R
2004.
Hopf duals, algebraic groups, and Jordan pairs.
Journal of Algebra,
Vol. 279,
Issue. 1,
p.
91.
Alberca Bjerregaard, Pablo
Loos, Ottmar
and
Martín González, Cándido
2005.
Derivations and automorphisms of Jordan algebras in characteristic two.
Journal of Algebra,
Vol. 285,
Issue. 1,
p.
146.
Ikai, Hisatoshi
2009.
An approach through big cells to Clifford groups of low rank.
Arkiv för Matematik,
Vol. 47,
Issue. 2,
p.
313.
IKAI, HISATOSHI
2010.
ON SUBGROUPS OF CLIFFORD GROUPS DEFINED BY JORDAN PAIRS OF RECTANGULAR MATRICES.
Journal of the Australian Mathematical Society,
Vol. 89,
Issue. 2,
p.
215.
Loos, Ottmar
and
Neher, Erhard
2010.
Steinberg groups for Jordan pairs.
Comptes Rendus. Mathématique,
Vol. 348,
Issue. 15-16,
p.
839.
Aranda-Orna, Diego
2017.
Fine gradings on simple exceptional Jordan pairs and triple systems.
Journal of Algebra,
Vol. 491,
Issue. ,
p.
517.
Boelaert, Lien
De Medts, Tom
and
Stavrova, Anastasia
2019.
Moufang Sets and Structurable Division Algebras.
Memoirs of the American Mathematical Society,
Vol. 259,
Issue. 1245,
Gross, Benedict H.
and
Garibaldi, Skip
2021.
Minuscule embeddings.
Indagationes Mathematicae,
Vol. 32,
Issue. 5,
p.
987.
Neher, Erhard
2021.
Interactions of Quantum Affine Algebras with Cluster Algebras, Current Algebras and Categorification.
Vol. 337,
Issue. ,
p.
77.
Alsaody, Seidon
2021.
Albert algebras over rings and related torsors.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 3,
p.
875.
 (iii) Ω = U+. H . U+ is open in G, and (iv) G is generated by H, U+, U+. This situation is characteristic for the complexifications of the automorphism groups of bounded symmetric domains (see, e.g., [9, 16]). A typical example is G = GLnwith (matrices being decomposed into 4 blocks) ψ given by
(iii) Ω = U+. H . U+ is open in G, and (iv) G is generated by H, U+, U+. This situation is characteristic for the complexifications of the automorphism groups of bounded symmetric domains (see, e.g., [9, 16]). A typical example is G = GLnwith (matrices being decomposed into 4 blocks) ψ given by