Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-04T09:32:46.432Z Has data issue: false hasContentIssue false
  • English
  • Français

On a θ-Weyl sum

Published online by Cambridge University Press:  22 January 2016

Yoshinobu Nakai
Yoshinobu Nakai*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We treat the sum 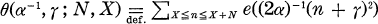, where α and γ are real with α positive. This sum was treated first by Hardy and Littlewood [4], and after them, by Behnke [1] and [2], Mordell [9], Wilton [11] and others. The reader will find its history in [7] and in the comments of the Collected Papers [4]. Here we show that the sum can be expressed explicitly, together with an error term O(N1/2), using the regular continued fraction expansion of α. As the statements have complications we will divide them into two theorems. In the followings all letters except ϑ, i, σ, ζ, χ and those in 3° are real, N is a positive real, and always k, n, a, A, B, C, D and E denote integers. The author expresses his thanks to Professor Tikao Tatuzawa and Professor Tomio Kubota for their encouragements.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 52 , December 1973 , pp. 163 - 172
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1973

References

[1] Behnke, H., Zur Theorie der diophantischen Approximationen, Part I, Abh. Math. Sem. Univ. Hamburg, 3 (1924), 261–318, with Corrigendum.Google Scholar
[2] Behnke, H., Part II, the same Abh., 4 (1926), 33–46.Google Scholar
[3] Eichler, M., Einführung in die Theorie der algebraischen Zahlen und Funktionen, Birkháuser Verlag, 1963.Google Scholar
[4] Hardy, G. H. and Littlewood, J. E., Some problems of Diophantine approximation II: The trigonometrical series associated with the elliptic θ-functions, Acta Math., 37=Collected Papers of G. H. Hardy, Vol. 1, 67–114.Google Scholar
[5] Jarnik, V. and Landau, E., Untersuchungen über einen van der Corputschen Satz, Math. Z., 39 (1935), 745–767.Google Scholar
[6] Khinchin, A. Ya., Continued fractions, The University of Chicago Press, 1964.Google Scholar
[7] Koksma, J. F., Diophantische Approximationen, Springer Verlag, 1936.Google Scholar
[8] Kubota, T., On a classical theta-function, Nagoya Math. J., 37 (1970), 183–189.Google Scholar
[9] Mordell, L. J., The approximate functional formula for the theta function, J. London Math. Soc, 1 (1926), 68–72.Google Scholar
[10] Titchmarsh, E. C., The theory of the Riemann Zeta-function, Oxford, 1951.Google Scholar
[11] Wilton, J. R., The approximate functional formula for the theta function, J. London Math. Soc, 2 (1927), 177–180.Google Scholar