Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gwinner, J.
and
Thalhammer, M.
2014.
Full Discretisations for Nonlinear Evolutionary Inequalities Based on Stiffly Accurate Runge–Kutta and hp-Finite Element Methods.
Foundations of Computational Mathematics,
Vol. 14,
Issue. 5,
p.
913.


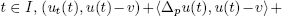
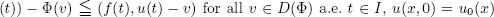 where Δ
where Δ