Article contents
A norm residue map for central extensions of an algebraic number field
Published online by Cambridge University Press: 22 January 2016
Extract
Let K be a finite Galois extension of an algebraic number field k with G = Gal (K/k), and M be a Galois extension of k containing K. We denote by 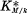 resp.
resp. 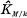 the genus field resp. the central class field of K with respect to M/k. By definition, the field
the genus field resp. the central class field of K with respect to M/k. By definition, the field 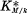 is the composite of K and the maximal abelian extension over k contained in M. The field
is the composite of K and the maximal abelian extension over k contained in M. The field 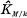 is the maximal Galois extension of k contained in M satisfying the condition that the Galois group over K is contained in the center of that over k. Then it is well known that Gal
is the maximal Galois extension of k contained in M satisfying the condition that the Galois group over K is contained in the center of that over k. Then it is well known that Gal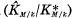 is isomorphic to a factor group of the Schur multiplicator H-3(G, Z), and is isomorphic to H-3(G, Z) when M is sufficiently large. In this case we call M abundant for K/k (See Heider [3, § 4] and Miyake [6, Theorem 5]).
is isomorphic to a factor group of the Schur multiplicator H-3(G, Z), and is isomorphic to H-3(G, Z) when M is sufficiently large. In this case we call M abundant for K/k (See Heider [3, § 4] and Miyake [6, Theorem 5]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1984
References
- 4
- Cited by


