Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2025-01-06T04:43:01.203Z Has data issue: false hasContentIssue false
  • English
  • Français

A NONDEGENERATE EXCHANGE MOVE ALWAYS PRODUCES INFINITELY MANY NONCONJUGATE BRAIDS

Part of: Low-dimensional topology

Published online by Cambridge University Press:  02 December 2019

TETSUYA ITO Open the ORCID record for TETSUYA ITO [Opens in a new window]
TETSUYA ITO*
Affiliation:
Department of Mathematics, Kyoto University, Kyoto606-8502, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if a link 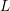$L$ has a closed $n$-braid representative admitting a nondegenerate exchange move, an exchange move that does not obviously preserve the conjugacy class, 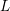$L$ has infinitely many nonconjugate closed $n$-braid representatives.

MSC classification

Primary: 57M25: Knots and links in $S^3$
Secondary: 57M27: Invariants of knots and 3-manifolds
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 205 - 208
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birman, J. and Menasco, W., Studying links via closed braids VI: a non-finiteness theorem, Pacific J. Math. 156 (1992), 265–285.CrossRefGoogle Scholar
Fathi, A., Dehn twists and pseudo-Anosov diffeomorphisms, Invent. Math. 87 (1987), 129–151.CrossRefGoogle Scholar
Shinjo, R., Non-conjugate braids whose closures result in the same knot, J. Knot Theory Ramifications 19 (2010), 117–124.CrossRefGoogle Scholar
Shinjo, R. and Stoimenow, A., Exchange moves and non-conjugate braid representatives of knots, Nagoya Math J. to appear, doi:10.1017/nmj.2019.10.Google Scholar
Stoimenow, A., On non-conjugate braids with the same closure link, J. Geom. 96 (2009), 179–186.CrossRefGoogle Scholar
Stoimenow, A., Non-conjugate braids with the same closure link from density of representations, J. Math. Pures Appl. 94(9) (2010), 470–496.CrossRefGoogle Scholar