Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-09T15:57:43.811Z Has data issue: false hasContentIssue false
  • English
  • Français

New Formulation of the Axiom of Choice by making use of the Comprehension Operator

Published online by Cambridge University Press:  22 January 2016

Katuzi Ono
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We have introduced in our former work [1] and [2] the comprehension operator “{·)”, which maps every binary relation to a binary relation. The definition of this operator

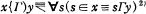
is remarkable in that it can be defined in any formal system having the membership relation ∈, which is hereafter called the universal system and is denoted by U. In this work, we would like to point out that the axiom of choice, in the strong sense as well as in the weak sense, can be formulated in an extremely simple style by making use of the comprehension operator.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 23 , December 1963 , pp. 53 - 71
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1963

References

[1] Ono, K., On a practical way of describing formal deductions. Nagoya Math. Journal. vol, 21, pp. 115–121 (1962).Google Scholar
[2] Ono, K., A stronger system of object theory as a prototype of set theory. Nagoya Math. Journal, vol. 22, pp. 119–167 (1963).Google Scholar
[3] Ono, K., A theory of mathematical objects as a prototype of set theory. Nagoya Math. Journal, vol. 20, pp. 105–168 (1962).Google Scholar
[4] Zermelo, E., Untersuchungen über die Grundlagen de Mengenlehre, I, Math. Ann., vol. 65, pp. 261–281 (1908).Google Scholar
[5] Fraenkel, A., Einleitung in die Mengenlehre, 1928 (3. Aufl.)Google Scholar
[6] Neumann, J. v., Die Axiomatisierung der Mengenlehre, I, J. für reine u. angew. Math., vol. 154, pp. 219–240 (1925). Die Axiomatisierung der Mengenlehre. Math. Z., vol. 26, pp. 1–46 (1927).Google Scholar
[7] Bernays, P., A system of axiomatic set theory, Part I-VII; Symbolic Logic; I, vol. 2, pp. 65–77 (1937); II, vol. 6, pp. 1–17 (1941), III, vol. 7, pp. 65–89 (1942); IV, vol. 7, pp. 133–145 (1942); V, vol. 8, pp. 89–106 (1943), VI, vol. 13, pp. 65–79 (1948); VII, vol. 19, pp, 81–96 (1954).Google Scholar
[8] Gödei, K., The consistency of the axiom of choice and of the generalized continuum hypothesis with the axioms of set theory. Annals of Mathematics Studies, No. 3, 1940.Google Scholar
[9] Gentzen, G., Untersuchungen über das logischen Schliessen. Math. Z., vol. 39, pp. 176–210, 405–431 (1935).Google Scholar