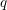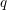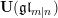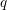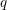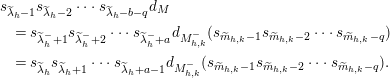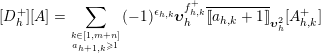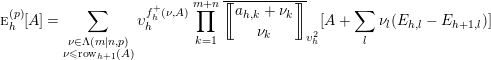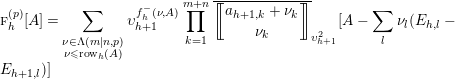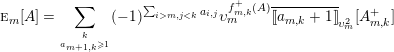1 Introduction
The beautiful Beilinson–Lusztig–MacPherson construction [Reference Beilinson, Lusztig and MacPherson1] of quantum
![]() $\mathfrak{g}\mathfrak{l}_{n}$
has been generalized to the quantum affine
$\mathfrak{g}\mathfrak{l}_{n}$
has been generalized to the quantum affine
![]() $\mathfrak{g}\mathfrak{l}_{n}$
[Reference Deng, Du and Fu4, Reference Du and Fu9], to the quantum super
$\mathfrak{g}\mathfrak{l}_{n}$
[Reference Deng, Du and Fu4, Reference Du and Fu9], to the quantum super
![]() $\mathfrak{g}\mathfrak{l}_{m|n}$
[Reference Du and Gu12], and partially to the other classical types [Reference Bao, Kujawa, Li and Wang2, Reference Fan and Li20] and affine type
$\mathfrak{g}\mathfrak{l}_{m|n}$
[Reference Du and Gu12], and partially to the other classical types [Reference Bao, Kujawa, Li and Wang2, Reference Fan and Li20] and affine type
![]() $C$
[Reference Fan, Lai, Li, Luo and Wang19], in which certain coideal subalgebras of quantum
$C$
[Reference Fan, Lai, Li, Luo and Wang19], in which certain coideal subalgebras of quantum
![]() $\mathfrak{g}\mathfrak{l}_{n}$
(or affine
$\mathfrak{g}\mathfrak{l}_{n}$
(or affine
![]() $\mathfrak{g}\mathfrak{l}_{n}$
) are used to form various quantum symmetric pairs associated with Hecke algebras of type
$\mathfrak{g}\mathfrak{l}_{n}$
) are used to form various quantum symmetric pairs associated with Hecke algebras of type
![]() $B/C/D$
or affine type
$B/C/D$
or affine type
![]() $C$
. A key step of these works is the establishment of certain multiplication formulas in the relevant
$C$
. A key step of these works is the establishment of certain multiplication formulas in the relevant
![]() $q$
-Schur algebras or Hecke endomorphism algebras. These formulas were originally derived by geometric methods. When the geometric approach is not available in the super case, a super version of the Curtis–Scott relative norm basis [Reference Du8, Reference Jones24], including a detailed analysis of the explicit action on the tensor space, is used in deriving such formulas; see [Reference Du and Gu12, Reference Du, Gu and Wang14, Reference Du, Gu and Wang15]. However, it is natural to expect the existence of a direct Hecke algebra method involving only the combinatorics of symmetric groups.
$q$
-Schur algebras or Hecke endomorphism algebras. These formulas were originally derived by geometric methods. When the geometric approach is not available in the super case, a super version of the Curtis–Scott relative norm basis [Reference Du8, Reference Jones24], including a detailed analysis of the explicit action on the tensor space, is used in deriving such formulas; see [Reference Du and Gu12, Reference Du, Gu and Wang14, Reference Du, Gu and Wang15]. However, it is natural to expect the existence of a direct Hecke algebra method involving only the combinatorics of symmetric groups.
In this paper, we will develop such a method. The multiplication formulas require to compute certain structure constants associated with the double coset basis, a basis defined by the double cosets of a symmetric group. Since a double coset can be described by a certain matrix with nonnegative integer entries, our first step is to find formulas, in terms of the matrix entries, of decomposing products of certain double cosets into disjoint unions of double cosets. We then use the findings to derive the multiplication formulas in
![]() $q$
-Schur superalgebras; see Theorem 4.1 and Corollary 4.2. This method simplifies the calculation in [Reference Du and Gu12, Sections 2–3] using relative norms.
$q$
-Schur superalgebras; see Theorem 4.1 and Corollary 4.2. This method simplifies the calculation in [Reference Du and Gu12, Sections 2–3] using relative norms.
The multiplication formulas result in several applications. The first one is the matrix representation of the regular representations over any commutative ring
![]() $R$
; see Theorem 4.5. When the ground ring
$R$
; see Theorem 4.5. When the ground ring
![]() $R$
is a field, we establish a criterion for the semisimplicity of
$R$
is a field, we establish a criterion for the semisimplicity of
![]() $q$
-Schur superalgebras (see Theorem 5.4), generalizing a quantum result of Erdmann and Nakano to the super case and a classical super result of Marko and Zubkov [Reference Marko and Zubkov26] (cf. [Reference Doty and Nakano6, Reference Erdmann and Nakano18]) to the quantum case. Finally, we introduce the infinitesimal and little
$q$
-Schur superalgebras (see Theorem 5.4), generalizing a quantum result of Erdmann and Nakano to the super case and a classical super result of Marko and Zubkov [Reference Marko and Zubkov26] (cf. [Reference Doty and Nakano6, Reference Erdmann and Nakano18]) to the quantum case. Finally, we introduce the infinitesimal and little
![]() $q$
-Schur superalgebras directly from the multiplication formulas (Theorem 6.1, Corollary 6.3). We also determine semisimple infinitesimal
$q$
-Schur superalgebras directly from the multiplication formulas (Theorem 6.1, Corollary 6.3). We also determine semisimple infinitesimal
![]() $q$
-Schur superalgebras and semisimple little
$q$
-Schur superalgebras and semisimple little
![]() $q$
-Schur superalgebras (Theorem 6.4).
$q$
-Schur superalgebras (Theorem 6.4).
It should be interesting to point out that, unlike the traditional methods used in [Reference Doty, Nakano and Peters7, Reference Du, Fu and Wang10], our definitions do not involve quantum enveloping algebras or quantum coordinate algebras and the semisimplicity proof is also independent of the representation theory of these ambient quantum groups or algebras. We expect that this combinatorial approach will give further applications to various
![]() $q$
-Schur superalgebras of other types in the near future.
$q$
-Schur superalgebras of other types in the near future.
2
 $q$
-Schur superalgebras
$q$
-Schur superalgebras
Let
![]() $W=\mathfrak{S}_{\{1,2,\ldots ,r\}}$
be the symmetric group on
$W=\mathfrak{S}_{\{1,2,\ldots ,r\}}$
be the symmetric group on
![]() $r$
letters and let
$r$
letters and let
![]() $S=\{s_{k}\mid 1\leqslant k<r\}$
be the set of basic transpositions
$S=\{s_{k}\mid 1\leqslant k<r\}$
be the set of basic transpositions
![]() $s_{k}=(k,k+1)$
. Denote the length function with respect to
$s_{k}=(k,k+1)$
. Denote the length function with respect to
![]() $S$
by
$S$
by
![]() $\ell :W\rightarrow \mathbb{N}$
.
$\ell :W\rightarrow \mathbb{N}$
.
Let
![]() $R$
be a commutative ring with 1 and let
$R$
be a commutative ring with 1 and let
![]() $q\in R^{\times }$
. The Hecke algebra
$q\in R^{\times }$
. The Hecke algebra
![]() ${\mathcal{H}}_{R}={\mathcal{H}}_{R}(W)$
is a free
${\mathcal{H}}_{R}={\mathcal{H}}_{R}(W)$
is a free
![]() $R$
-module with basis
$R$
-module with basis
![]() $\{T_{w}\mid w\in W\}$
and the multiplication defined by the rules: for
$\{T_{w}\mid w\in W\}$
and the multiplication defined by the rules: for
![]() $s\in S$
,
$s\in S$
,
The Hecke algebra over
![]() $R={\mathcal{Z}}:=\mathbb{Z}[\boldsymbol{\unicode[STIX]{x1D710}},\boldsymbol{\unicode[STIX]{x1D710}}^{-1}]$
and
$R={\mathcal{Z}}:=\mathbb{Z}[\boldsymbol{\unicode[STIX]{x1D710}},\boldsymbol{\unicode[STIX]{x1D710}}^{-1}]$
and
![]() $q=\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
is simply denoted by
$q=\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
is simply denoted by
![]() ${\mathcal{H}}$
.
${\mathcal{H}}$
.
Let
![]() $W_{\unicode[STIX]{x1D706}}$
denote the parabolic subgroup of
$W_{\unicode[STIX]{x1D706}}$
denote the parabolic subgroup of
![]() $W$
associated with
$W$
associated with
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N})\in \unicode[STIX]{x1D6EC}(N,r)$
where
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N})\in \unicode[STIX]{x1D6EC}(N,r)$
where
Then
![]() $W_{\unicode[STIX]{x1D706}}$
consists of permutations that leave invariant the following sets of integers
$W_{\unicode[STIX]{x1D706}}$
consists of permutations that leave invariant the following sets of integers
Let
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D706}}:={\mathcal{D}}_{W_{\unicode[STIX]{x1D706}}}$
be the set of all shortest coset representatives of the right cosets of
${\mathcal{D}}_{\unicode[STIX]{x1D706}}:={\mathcal{D}}_{W_{\unicode[STIX]{x1D706}}}$
be the set of all shortest coset representatives of the right cosets of
![]() $W_{\unicode[STIX]{x1D706}}$
in
$W_{\unicode[STIX]{x1D706}}$
in
![]() $W$
. Let
$W$
. Let
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}={\mathcal{D}}_{\unicode[STIX]{x1D706}}\cap {\mathcal{D}}_{\unicode[STIX]{x1D707}}^{-1}$
be the set of the shortest
${\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}={\mathcal{D}}_{\unicode[STIX]{x1D706}}\cap {\mathcal{D}}_{\unicode[STIX]{x1D707}}^{-1}$
be the set of the shortest
![]() $W_{\unicode[STIX]{x1D706}}$
–
$W_{\unicode[STIX]{x1D706}}$
–
![]() $W_{\unicode[STIX]{x1D707}}$
double coset representatives.
$W_{\unicode[STIX]{x1D707}}$
double coset representatives.
For
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(N,r)$
and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(N,r)$
and
![]() $d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
, the subgroup
$d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
, the subgroup
![]() $W_{\unicode[STIX]{x1D706}}^{d}\cap W_{\unicode[STIX]{x1D707}}=d^{-1}W_{\unicode[STIX]{x1D706}}d\cap W_{\unicode[STIX]{x1D707}}$
is a parabolic subgroup associated with a composition, which is denoted by
$W_{\unicode[STIX]{x1D706}}^{d}\cap W_{\unicode[STIX]{x1D707}}=d^{-1}W_{\unicode[STIX]{x1D706}}d\cap W_{\unicode[STIX]{x1D707}}$
is a parabolic subgroup associated with a composition, which is denoted by
![]() $\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
. In other words, we define
$\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
. In other words, we define
The composition
![]() $\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
can be easily described in terms of the following
$\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
can be easily described in terms of the following
![]() $N\times N$
-matrix
$N\times N$
-matrix
![]() $A=(a_{i,j})$
with
$A=(a_{i,j})$
with
![]() $a_{i,j}=|\mathbb{N}_{i}^{\unicode[STIX]{x1D706}}\cap d(\mathbb{N}_{j}^{\unicode[STIX]{x1D707}})|$
: if
$a_{i,j}=|\mathbb{N}_{i}^{\unicode[STIX]{x1D706}}\cap d(\mathbb{N}_{j}^{\unicode[STIX]{x1D707}})|$
: if
![]() $\unicode[STIX]{x1D708}^{(j)}=(a_{1,j},a_{2,j},\ldots ,a_{N,j})$
denotes the
$\unicode[STIX]{x1D708}^{(j)}=(a_{1,j},a_{2,j},\ldots ,a_{N,j})$
denotes the
![]() $j$
th column of
$j$
th column of
![]() $A$
, then
$A$
, then
Putting
![]() $\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})=(|\mathbb{N}_{i}^{\unicode[STIX]{x1D706}}\cap d(\mathbb{N}_{j}^{\unicode[STIX]{x1D707}})|)_{i,j}$
, we obtain a bijection
$\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})=(|\mathbb{N}_{i}^{\unicode[STIX]{x1D706}}\cap d(\mathbb{N}_{j}^{\unicode[STIX]{x1D707}})|)_{i,j}$
, we obtain a bijection
where
![]() $M(N,r)$
is the set of all
$M(N,r)$
is the set of all
![]() $N\times N$
matrices
$N\times N$
matrices
![]() $A=(a_{i,j})$
over
$A=(a_{i,j})$
over
![]() $\mathbb{N}$
whose entries sum to
$\mathbb{N}$
whose entries sum to
![]() $r$
, i.e.,
$r$
, i.e.,
![]() $|A|:=\sum _{i,j}a_{i,j}=r$
.
$|A|:=\sum _{i,j}a_{i,j}=r$
.
For
![]() $A\in M(N,r)$
, if
$A\in M(N,r)$
, if
![]() $\jmath ^{-1}(A)=(\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})$
, then
$\jmath ^{-1}(A)=(\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})$
, then
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(N,r)$
and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(N,r)$
and
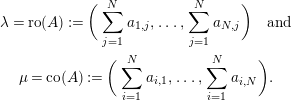 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D706}=\text{ro}(A):=\bigg(\mathop{\sum }_{j=1}^{N}a_{1,j},\ldots ,\mathop{\sum }_{j=1}^{N}a_{N,j}\bigg)\quad \text{and}\\ \displaystyle \unicode[STIX]{x1D707}=\text{co}(A):=\bigg(\mathop{\sum }_{i=1}^{N}a_{i,1},\ldots ,\mathop{\sum }_{i=1}^{N}a_{i,N}\bigg).\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D706}=\text{ro}(A):=\bigg(\mathop{\sum }_{j=1}^{N}a_{1,j},\ldots ,\mathop{\sum }_{j=1}^{N}a_{N,j}\bigg)\quad \text{and}\\ \displaystyle \unicode[STIX]{x1D707}=\text{co}(A):=\bigg(\mathop{\sum }_{i=1}^{N}a_{i,1},\ldots ,\mathop{\sum }_{i=1}^{N}a_{i,N}\bigg).\end{array} & & \displaystyle\end{eqnarray}$$
For the definition of
![]() $q$
-Schur superalgebra, we fix two nonnegative integers
$q$
-Schur superalgebra, we fix two nonnegative integers
![]() $m,n$
and assume
$m,n$
and assume
![]() $R$
has characteristic
$R$
has characteristic
![]() $\neq 2$
. We also need the parity function
$\neq 2$
. We also need the parity function
A composition
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $m+n$
parts will be written
$m+n$
parts will be written
to indicate the “even” and “odd” parts of
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
For
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}^{(0)}\mid \unicode[STIX]{x1D706}^{(1)})\in \unicode[STIX]{x1D6EC}(m|n,r)$
, we also write
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}^{(0)}\mid \unicode[STIX]{x1D706}^{(1)})\in \unicode[STIX]{x1D6EC}(m|n,r)$
, we also write
where
![]() $W_{\unicode[STIX]{x1D706}^{(0)}}\leqslant \mathfrak{S}_{\{1,2,\ldots ,|\unicode[STIX]{x1D706}^{(0)}|\}}$
and
$W_{\unicode[STIX]{x1D706}^{(0)}}\leqslant \mathfrak{S}_{\{1,2,\ldots ,|\unicode[STIX]{x1D706}^{(0)}|\}}$
and
![]() $W_{\unicode[STIX]{x1D706}^{(1)}}\leqslant \mathfrak{S}_{\{|\unicode[STIX]{x1D706}^{(0)}|+1,\ldots ,r\}}$
are the even and odd parts of
$W_{\unicode[STIX]{x1D706}^{(1)}}\leqslant \mathfrak{S}_{\{|\unicode[STIX]{x1D706}^{(0)}|+1,\ldots ,r\}}$
are the even and odd parts of
![]() $W_{\unicode[STIX]{x1D706}}$
, respectively.
$W_{\unicode[STIX]{x1D706}}$
, respectively.
Denote the Hecke algebra associated with the parabolic subgroup
![]() $W_{\unicode[STIX]{x1D706}}$
by
$W_{\unicode[STIX]{x1D706}}$
by
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
, which is spanned by
${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
, which is spanned by
![]() $T_{w},w\in W_{\unicode[STIX]{x1D706}}$
. The elements in
$T_{w},w\in W_{\unicode[STIX]{x1D706}}$
. The elements in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
where, for
![]() $i=0,1$
,
$i=0,1$
,
generate
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
-modules
${\mathcal{H}}_{\unicode[STIX]{x1D706}}$
-modules
![]() $R[xy]_{\unicode[STIX]{x1D706}}$
,
$R[xy]_{\unicode[STIX]{x1D706}}$
,
![]() $R[yx]_{\unicode[STIX]{x1D706}}$
. Define the “tensor space” (cf. [Reference Du and Rui16, (8.3.4)])
$R[yx]_{\unicode[STIX]{x1D706}}$
. Define the “tensor space” (cf. [Reference Du and Rui16, (8.3.4)])
By the definition in [Reference Du and Rui16], the endomorphism algebra
is called a
![]() $q$
-Schur superalgebra whose
$q$
-Schur superalgebra whose
![]() $\mathbb{Z}_{2}$
-graded structure is given by
$\mathbb{Z}_{2}$
-graded structure is given by
We will use the notation
![]() ${\mathcal{S}}(m|n,r)$
to denote the
${\mathcal{S}}(m|n,r)$
to denote the
![]() $\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
-Schur algebra over
$\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
-Schur algebra over
![]() ${\mathcal{Z}}$
.
${\mathcal{Z}}$
.
We now describe a characteristic-free basis for
![]() ${\mathcal{S}}_{R}(m|n,r)$
.
${\mathcal{S}}_{R}(m|n,r)$
.
For
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, let
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, let
This set is the super version of the usual
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
. We need the following subsets of the
${\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
. We need the following subsets of the
![]() $(m+n)\times (m+n)$
matrix ring
$(m+n)\times (m+n)$
matrix ring
![]() $M_{m+n}(\mathbb{N})$
over
$M_{m+n}(\mathbb{N})$
over
![]() $\mathbb{N}$
:
$\mathbb{N}$
:
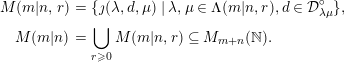 $$\begin{eqnarray}\displaystyle M(m|n,r) & = & \displaystyle \{\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})\mid \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r),d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\circ }\},\nonumber\\ \displaystyle M(m|n) & = & \displaystyle \mathop{\bigcup }_{r\geqslant 0}M(m|n,r)\subseteq M_{m+n}(\mathbb{N}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M(m|n,r) & = & \displaystyle \{\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})\mid \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r),d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\circ }\},\nonumber\\ \displaystyle M(m|n) & = & \displaystyle \mathop{\bigcup }_{r\geqslant 0}M(m|n,r)\subseteq M_{m+n}(\mathbb{N}).\end{eqnarray}$$
Following [Reference Du and Rui16, (5.3.2)], define, for
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r)$
and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}(m|n,r)$
and
![]() $d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\circ }$
,
$d\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{\circ }$
,
where
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}$
,
![]() $\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D707}d^{-1}\cap \unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D707}d^{-1}\cap \unicode[STIX]{x1D706}$
, and
for any
![]() $D\subseteq W$
(
$D\subseteq W$
(
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}$
or
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}$
or
![]() $\unicode[STIX]{x1D707}$
) with
$\unicode[STIX]{x1D707}$
) with
![]() $D_{i}=D\cap W_{\unicode[STIX]{x1D702}^{(i)}}$
(cf. [Reference Du and Rui16, (5.3.2)]).
$D_{i}=D\cap W_{\unicode[STIX]{x1D702}^{(i)}}$
(cf. [Reference Du and Rui16, (5.3.2)]).
The element
![]() $T_{W_{\unicode[STIX]{x1D706}}dW_{\unicode[STIX]{x1D707}}}$
is used to define an
$T_{W_{\unicode[STIX]{x1D706}}dW_{\unicode[STIX]{x1D707}}}$
is used to define an
![]() ${\mathcal{H}}_{R}$
-module homomorphism
${\mathcal{H}}_{R}$
-module homomorphism
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{d}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{d}$
on
![]() $\mathfrak{T}_{R}(m|n,r)$
:
$\mathfrak{T}_{R}(m|n,r)$
:
The first assertion of the following result is given in [Reference Du and Rui16, 5.8], while the last assertion for the nonquantum case was observed in [Reference Hemmer, Kujawa and Nakano23, Section 3.1]. Write
![]() $\unicode[STIX]{x1D719}_{A}:=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{d}$
if
$\unicode[STIX]{x1D719}_{A}:=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}^{d}$
if
![]() $A=\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})$
.
$A=\jmath (\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707})$
.
Lemma 2.1. The set
![]() $\{\unicode[STIX]{x1D719}_{A}\mid A\in M(m|n,r)\}$
forms an
$\{\unicode[STIX]{x1D719}_{A}\mid A\in M(m|n,r)\}$
forms an
![]() $R$
-basis for
$R$
-basis for
![]() ${\mathcal{S}}_{R}(m|n,r)$
. Hence,
${\mathcal{S}}_{R}(m|n,r)$
. Hence,
![]() ${\mathcal{S}}_{R}(m|n,r)\cong {\mathcal{S}}(m|n,r)\otimes _{{\mathcal{Z}}}R$
. Moreover, there is an
${\mathcal{S}}_{R}(m|n,r)\cong {\mathcal{S}}(m|n,r)\otimes _{{\mathcal{Z}}}R$
. Moreover, there is an
![]() $R$
-algebra isomorphism
$R$
-algebra isomorphism
Proof. We only need to prove the last assertion. The Hecke algebra
![]() ${\mathcal{H}}_{R}$
admits an
${\mathcal{H}}_{R}$
admits an
![]() $R$
-algebra involutory automorphism
$R$
-algebra involutory automorphism
![]() $\unicode[STIX]{x1D711}$
sending
$\unicode[STIX]{x1D711}$
sending
![]() $T_{s}$
to
$T_{s}$
to
![]() $-qT_{s}^{-1}=(q-1)-T_{s}$
for all
$-qT_{s}^{-1}=(q-1)-T_{s}$
for all
![]() $s\in S$
. Since
$s\in S$
. Since
![]() $\unicode[STIX]{x1D711}(x_{\unicode[STIX]{x1D706}})=q^{\ell (w_{0,\unicode[STIX]{x1D706}})}y_{\unicode[STIX]{x1D706}}$
, where
$\unicode[STIX]{x1D711}(x_{\unicode[STIX]{x1D706}})=q^{\ell (w_{0,\unicode[STIX]{x1D706}})}y_{\unicode[STIX]{x1D706}}$
, where
![]() $w_{0,\unicode[STIX]{x1D706}}$
is the longest element in
$w_{0,\unicode[STIX]{x1D706}}$
is the longest element in
![]() $W_{\unicode[STIX]{x1D706}}$
(see, e.g., [Reference Deng, Du, Parshall and Wang5, (7.6.2)]), we have
$W_{\unicode[STIX]{x1D706}}$
(see, e.g., [Reference Deng, Du, Parshall and Wang5, (7.6.2)]), we have
![]() $\unicode[STIX]{x1D711}([xy]_{\unicode[STIX]{x1D706}})=\unicode[STIX]{x1D711}(x_{\unicode[STIX]{x1D706}^{(0)}}y_{\unicode[STIX]{x1D706}^{(1)}})=q^{\ell (w_{0,\unicode[STIX]{x1D706}^{(0)}})-\ell (w_{0,\unicode[STIX]{x1D706}^{(1)}})}y_{\unicode[STIX]{x1D706}^{(0)}}x_{\unicode[STIX]{x1D706}^{(1)}}$
. If we denote by
$\unicode[STIX]{x1D711}([xy]_{\unicode[STIX]{x1D706}})=\unicode[STIX]{x1D711}(x_{\unicode[STIX]{x1D706}^{(0)}}y_{\unicode[STIX]{x1D706}^{(1)}})=q^{\ell (w_{0,\unicode[STIX]{x1D706}^{(0)}})-\ell (w_{0,\unicode[STIX]{x1D706}^{(1)}})}y_{\unicode[STIX]{x1D706}^{(0)}}x_{\unicode[STIX]{x1D706}^{(1)}}$
. If we denote by
![]() $([xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R})^{\unicode[STIX]{x1D711}}$
the module obtained by twisting the action on
$([xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R})^{\unicode[STIX]{x1D711}}$
the module obtained by twisting the action on
![]() $[xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R}$
by
$[xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R}$
by
![]() $\unicode[STIX]{x1D711}$
, i.e.,
$\unicode[STIX]{x1D711}$
, i.e.,
![]() $([xy]_{\unicode[STIX]{x1D706}}h)\ast h^{\prime }=([xy]_{\unicode[STIX]{x1D706}}h)\unicode[STIX]{x1D711}(h^{\prime })$
for all
$([xy]_{\unicode[STIX]{x1D706}}h)\ast h^{\prime }=([xy]_{\unicode[STIX]{x1D706}}h)\unicode[STIX]{x1D711}(h^{\prime })$
for all
![]() $h,h^{\prime }\in {\mathcal{H}}_{R}$
, then the map
$h,h^{\prime }\in {\mathcal{H}}_{R}$
, then the map
is an
![]() ${\mathcal{H}}_{R}$
module isomorphism. These
${\mathcal{H}}_{R}$
module isomorphism. These
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
induce an
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
induce an
![]() ${\mathcal{H}}_{R}$
module isomorphism
${\mathcal{H}}_{R}$
module isomorphism
![]() $\unicode[STIX]{x1D6F7}:\mathfrak{T}_{R}(m|n,r)^{\unicode[STIX]{x1D711}}\longrightarrow \mathfrak{T}_{R}(n|m,r).$
Now the required isomorphism follows.
$\unicode[STIX]{x1D6F7}:\mathfrak{T}_{R}(m|n,r)^{\unicode[STIX]{x1D711}}\longrightarrow \mathfrak{T}_{R}(n|m,r).$
Now the required isomorphism follows.
3 Decomposing products of double cosets
Throughout the section, let
![]() $W$
be the symmetric group and let
$W$
be the symmetric group and let
![]() $n,r$
be positive integers. We also fix the following notation in this section:
$n,r$
be positive integers. We also fix the following notation in this section:
 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\displaystyle M=(m_{ij})\in M(n,r)\quad \text{with }\jmath ^{-1}(M)=(\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707}),\quad d_{M}:=d,\\ \displaystyle \unicode[STIX]{x1D708}_{M}:=\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}=(m_{1,1},m_{2,1},\ldots ,m_{n,1},\ldots ,m_{1,n},m_{2,n},\ldots ,m_{n,n}),\\ \displaystyle \unicode[STIX]{x1D70E}_{i,j}=\mathop{\sum }_{k=1}^{j-1}\mathop{\sum }_{h=1}^{n}m_{h,k}+\mathop{\sum }_{k\leqslant i,l\geqslant j}m_{k,l},\\ \displaystyle M_{h,k}^{+}=M+E_{h,k}-E_{h+1,k}\quad \text{if }m_{h+1,k}\geqslant 1,\\ \displaystyle M_{h,k}^{-}=M-E_{h,k}+E_{h+1,k}\quad \text{if }m_{h,k}\geqslant 1.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\displaystyle M=(m_{ij})\in M(n,r)\quad \text{with }\jmath ^{-1}(M)=(\unicode[STIX]{x1D706},d,\unicode[STIX]{x1D707}),\quad d_{M}:=d,\\ \displaystyle \unicode[STIX]{x1D708}_{M}:=\unicode[STIX]{x1D706}d\cap \unicode[STIX]{x1D707}=(m_{1,1},m_{2,1},\ldots ,m_{n,1},\ldots ,m_{1,n},m_{2,n},\ldots ,m_{n,n}),\\ \displaystyle \unicode[STIX]{x1D70E}_{i,j}=\mathop{\sum }_{k=1}^{j-1}\mathop{\sum }_{h=1}^{n}m_{h,k}+\mathop{\sum }_{k\leqslant i,l\geqslant j}m_{k,l},\\ \displaystyle M_{h,k}^{+}=M+E_{h,k}-E_{h+1,k}\quad \text{if }m_{h+1,k}\geqslant 1,\\ \displaystyle M_{h,k}^{-}=M-E_{h,k}+E_{h+1,k}\quad \text{if }m_{h,k}\geqslant 1.\end{array}\right. & & \displaystyle\end{eqnarray}$$
Moreover, to any sequence
![]() $(a_{1},a_{2},\ldots ,a_{n})$
, we associate its partial sum sequence
$(a_{1},a_{2},\ldots ,a_{n})$
, we associate its partial sum sequence
![]() $(\widetilde{a}_{1},\widetilde{a}_{2},\ldots ,\widetilde{a}_{n})$
with
$(\widetilde{a}_{1},\widetilde{a}_{2},\ldots ,\widetilde{a}_{n})$
with
![]() $\widetilde{a}_{i}=a_{1}+\cdots +a_{i}$
. Thus,
$\widetilde{a}_{i}=a_{1}+\cdots +a_{i}$
. Thus,
![]() $\widetilde{\unicode[STIX]{x1D706}}_{i}=\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i}$
and
$\widetilde{\unicode[STIX]{x1D706}}_{i}=\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i}$
and
![]() $\widetilde{m}_{i,j}$
is the partial sum at the
$\widetilde{m}_{i,j}$
is the partial sum at the
![]() $(i,j)$
-position of
$(i,j)$
-position of
![]() $\unicode[STIX]{x1D708}_{M}$
. We also note that
$\unicode[STIX]{x1D708}_{M}$
. We also note that
![]() $\unicode[STIX]{x1D70E}_{i,j}=\widetilde{\unicode[STIX]{x1D707}}_{j-1}+m_{i,j}^{\llcorner }$
, where
$\unicode[STIX]{x1D70E}_{i,j}=\widetilde{\unicode[STIX]{x1D707}}_{j-1}+m_{i,j}^{\llcorner }$
, where
![]() $m_{i,j}^{\llcorner }=\sum _{k\leqslant i,l\geqslant j}a_{k,l}$
. In particular,
$m_{i,j}^{\llcorner }=\sum _{k\leqslant i,l\geqslant j}a_{k,l}$
. In particular,
![]() $\unicode[STIX]{x1D70E}_{i,1}=m_{i,1}^{\llcorner }=\widetilde{\unicode[STIX]{x1D706}}_{i}$
.
$\unicode[STIX]{x1D70E}_{i,1}=m_{i,1}^{\llcorner }=\widetilde{\unicode[STIX]{x1D706}}_{i}$
.
The following result will be proved at the end of the section.
Theorem 3.1. Maintain the notation in (3.0.1) with
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})$
and, for
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})$
and, for
![]() $1\leqslant h\leqslant n$
, let
$1\leqslant h\leqslant n$
, let
![]() $\unicode[STIX]{x1D706}^{[h^{\pm }]}:=\unicode[STIX]{x1D706}\pm \mathbf{e}_{h}\mp \mathbf{e}_{h+1}=\text{ro}(M_{h,k}^{\pm })$
, where
$\unicode[STIX]{x1D706}^{[h^{\pm }]}:=\unicode[STIX]{x1D706}\pm \mathbf{e}_{h}\mp \mathbf{e}_{h+1}=\text{ro}(M_{h,k}^{\pm })$
, where
![]() $\mathbf{e}_{i}=(\unicode[STIX]{x1D6FF}_{1,i},\ldots ,\unicode[STIX]{x1D6FF}_{n,i})$
. Then
$\mathbf{e}_{i}=(\unicode[STIX]{x1D6FF}_{1,i},\ldots ,\unicode[STIX]{x1D6FF}_{n,i})$
. Then
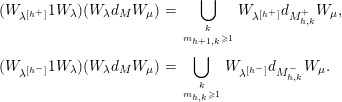 $$\begin{eqnarray}\displaystyle (W_{\unicode[STIX]{x1D706}^{[h^{+}]}}1W_{\unicode[STIX]{x1D706}})(W_{\unicode[STIX]{x1D706}}d_{M}W_{\unicode[STIX]{x1D707}}) & = & \displaystyle \mathop{\bigcup }_{{k\atop m_{h+1,k}\geqslant 1}}W_{\unicode[STIX]{x1D706}^{[h^{+}]}}d_{M_{h,k}^{+}}W_{\unicode[STIX]{x1D707}},\nonumber\\ \displaystyle (W_{\unicode[STIX]{x1D706}^{[h^{-}]}}1W_{\unicode[STIX]{x1D706}})(W_{\unicode[STIX]{x1D706}}d_{M}W_{\unicode[STIX]{x1D707}}) & = & \displaystyle \mathop{\bigcup }_{{k\atop m_{h,k}\geqslant 1}}W_{\unicode[STIX]{x1D706}^{[h^{-}]}}d_{M_{h,k}^{-}}W_{\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (W_{\unicode[STIX]{x1D706}^{[h^{+}]}}1W_{\unicode[STIX]{x1D706}})(W_{\unicode[STIX]{x1D706}}d_{M}W_{\unicode[STIX]{x1D707}}) & = & \displaystyle \mathop{\bigcup }_{{k\atop m_{h+1,k}\geqslant 1}}W_{\unicode[STIX]{x1D706}^{[h^{+}]}}d_{M_{h,k}^{+}}W_{\unicode[STIX]{x1D707}},\nonumber\\ \displaystyle (W_{\unicode[STIX]{x1D706}^{[h^{-}]}}1W_{\unicode[STIX]{x1D706}})(W_{\unicode[STIX]{x1D706}}d_{M}W_{\unicode[STIX]{x1D707}}) & = & \displaystyle \mathop{\bigcup }_{{k\atop m_{h,k}\geqslant 1}}W_{\unicode[STIX]{x1D706}^{[h^{-}]}}d_{M_{h,k}^{-}}W_{\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$
We first describe some standard reduced expression for
![]() $d_{M}$
.
$d_{M}$
.
If
![]() $m_{i,j}=0$
, or
$m_{i,j}=0$
, or
![]() $m_{i,j}>0$
but
$m_{i,j}>0$
but
![]() $\unicode[STIX]{x1D70E}_{i-1,j}=\widetilde{m}_{i-1,j}$
(i.e.,
$\unicode[STIX]{x1D70E}_{i-1,j}=\widetilde{m}_{i-1,j}$
(i.e.,
![]() $m_{i-1,j+1}^{\llcorner }=0$
), set
$m_{i-1,j+1}^{\llcorner }=0$
), set
![]() $w_{i,j}=1$
; if
$w_{i,j}=1$
; if
![]() $m_{i,j}>0$
and
$m_{i,j}>0$
and
![]() $\unicode[STIX]{x1D70E}_{i-1,j}>\widetilde{m}_{i-1,j}$
, let
$\unicode[STIX]{x1D70E}_{i-1,j}>\widetilde{m}_{i-1,j}$
, let
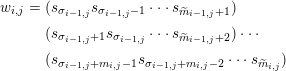 $$\begin{eqnarray}\displaystyle w_{i,j} & = & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}}s_{\unicode[STIX]{x1D70E}_{i-1,j}-1}\cdots s_{\widetilde{m}_{i-1,j}+1})\nonumber\\ \displaystyle & & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}}\cdots s_{\widetilde{m}_{i-1,j}+2})\cdots \nonumber\\ \displaystyle & & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-2}\cdots s_{\widetilde{m}_{i,j}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{i,j} & = & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}}s_{\unicode[STIX]{x1D70E}_{i-1,j}-1}\cdots s_{\widetilde{m}_{i-1,j}+1})\nonumber\\ \displaystyle & & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}}\cdots s_{\widetilde{m}_{i-1,j}+2})\cdots \nonumber\\ \displaystyle & & \displaystyle (s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-2}\cdots s_{\widetilde{m}_{i,j}})\end{eqnarray}$$
and
![]() $w_{i,j}^{+}=s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+2}\cdots s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}}w_{i,j}$
(and
$w_{i,j}^{+}=s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+2}\cdots s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}}w_{i,j}$
(and
![]() $w_{i,j}^{+}=1$
if
$w_{i,j}^{+}=1$
if
![]() $m_{i,j}=0$
). Note that we may rewrite
$m_{i,j}=0$
). Note that we may rewrite
![]() $w_{i,j}^{+}$
as
$w_{i,j}^{+}$
as
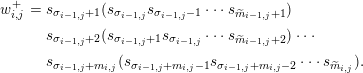 $$\begin{eqnarray}\displaystyle w_{i,j}^{+} & = & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}(s_{\unicode[STIX]{x1D70E}_{i-1,j}}s_{\unicode[STIX]{x1D70E}_{i-1,j}-1}\cdots s_{\widetilde{m}_{i-1,j}+1})\nonumber\\ \displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+2}(s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}}\cdots s_{\widetilde{m}_{i-1,j}+2})\cdots \nonumber\\ \displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}}(s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-2}\cdots s_{\widetilde{m}_{i,j}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{i,j}^{+} & = & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}(s_{\unicode[STIX]{x1D70E}_{i-1,j}}s_{\unicode[STIX]{x1D70E}_{i-1,j}-1}\cdots s_{\widetilde{m}_{i-1,j}+1})\nonumber\\ \displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+2}(s_{\unicode[STIX]{x1D70E}_{i-1,j}+1}s_{\unicode[STIX]{x1D70E}_{i-1,j}}\cdots s_{\widetilde{m}_{i-1,j}+2})\cdots \nonumber\\ \displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}}(s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-1}s_{\unicode[STIX]{x1D70E}_{i-1,j}+m_{i,j}-2}\cdots s_{\widetilde{m}_{i,j}}).\end{eqnarray}$$
For example, if
![]() $M=\left(\begin{smallmatrix}1 & 3 & 2\\ 2 & 1 & 1\\ 1 & 0 & 2\end{smallmatrix}\right)$
then
$M=\left(\begin{smallmatrix}1 & 3 & 2\\ 2 & 1 & 1\\ 1 & 0 & 2\end{smallmatrix}\right)$
then
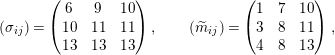 $$\begin{eqnarray}(\unicode[STIX]{x1D70E}_{ij})=\left(\begin{array}{@{}ccc@{}}6 & 9 & 10\\ 10 & 11 & 11\\ 13 & 13 & 13\end{array}\right),\qquad (\widetilde{m}_{ij})=\left(\begin{array}{@{}ccc@{}}1 & 7 & 10\\ 3 & 8 & 11\\ 4 & 8 & 13\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E}_{ij})=\left(\begin{array}{@{}ccc@{}}6 & 9 & 10\\ 10 & 11 & 11\\ 13 & 13 & 13\end{array}\right),\qquad (\widetilde{m}_{ij})=\left(\begin{array}{@{}ccc@{}}1 & 7 & 10\\ 3 & 8 & 11\\ 4 & 8 & 13\end{array}\right),\end{eqnarray}$$
and
![]() $w_{3,1}=s_{10}s_{9}\cdots s_{4}=\left(\begin{smallmatrix}4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\ 11 & 4 & 5 & 6 & 7 & 8 & 9 & 10\end{smallmatrix}\right)$
, and
$w_{3,1}=s_{10}s_{9}\cdots s_{4}=\left(\begin{smallmatrix}4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\ 11 & 4 & 5 & 6 & 7 & 8 & 9 & 10\end{smallmatrix}\right)$
, and
![]() $w_{2,2}=s_{9}s_{8}=\left(\begin{smallmatrix}8 & 9 & 10\\ 10 & 8 & 9\end{smallmatrix}\right)$
,
$w_{2,2}=s_{9}s_{8}=\left(\begin{smallmatrix}8 & 9 & 10\\ 10 & 8 & 9\end{smallmatrix}\right)$
,
![]() $w_{3,2}=1$
, then
$w_{3,2}=1$
, then
![]() $w_{2,1}w_{3,1}w_{2,2}w_{3,2}=\left(\begin{smallmatrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13\\ 1 & 7 & 8 & 11 & 2 & 3 & 4 & 9 & 5 & 6 & 10 & 12 & 13\end{smallmatrix}\right)$
, which is
$w_{2,1}w_{3,1}w_{2,2}w_{3,2}=\left(\begin{smallmatrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13\\ 1 & 7 & 8 & 11 & 2 & 3 & 4 & 9 & 5 & 6 & 10 & 12 & 13\end{smallmatrix}\right)$
, which is
![]() $d_{M}$
.
$d_{M}$
.
Lemma 3.2. [Reference Du and Gu12, Algorithm 2.1]
Let
![]() $M$
,
$M$
,
![]() $d_{M}$
and
$d_{M}$
and
![]() $M_{h,k}^{+}$
be given as in (3.0.1). Then a reduced expression of
$M_{h,k}^{+}$
be given as in (3.0.1). Then a reduced expression of
![]() $d_{M}$
is of the form
$d_{M}$
is of the form
If
![]() $m_{h+1,k}\geqslant 1$
, then
$m_{h+1,k}\geqslant 1$
, then
where, for almost all
![]() $i,j$
,
$i,j$
,
![]() $w_{ij}^{\prime }=w_{ij}$
, except
$w_{ij}^{\prime }=w_{ij}$
, except
![]() $w_{h+1,j}^{\prime }=w_{h+1,j}^{+}$
for
$w_{h+1,j}^{\prime }=w_{h+1,j}^{+}$
for
![]() $j<k$
and
$j<k$
and
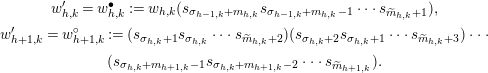 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle w_{h,k}^{\prime }=w_{h,k}^{\bullet }:=w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}}s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}-1}\cdots s_{\widetilde{m}_{h,k}+1}),\\ \displaystyle w_{h+1,k}^{\prime }=w_{h+1,k}^{\circ }:=(s_{\unicode[STIX]{x1D70E}_{h,k}+1}s_{\unicode[STIX]{x1D70E}_{h,k}}\cdots s_{\widetilde{m}_{h,k}+2})(s_{\unicode[STIX]{x1D70E}_{h,k}+2}s_{\unicode[STIX]{x1D70E}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+3})\cdots \\ \displaystyle (s_{\unicode[STIX]{x1D70E}_{h,k}+m_{h+1,k}-1}s_{\unicode[STIX]{x1D70E}_{h,k}+m_{h+1,k}-2}\cdots s_{\widetilde{m}_{h+1,k}}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle w_{h,k}^{\prime }=w_{h,k}^{\bullet }:=w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}}s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}-1}\cdots s_{\widetilde{m}_{h,k}+1}),\\ \displaystyle w_{h+1,k}^{\prime }=w_{h+1,k}^{\circ }:=(s_{\unicode[STIX]{x1D70E}_{h,k}+1}s_{\unicode[STIX]{x1D70E}_{h,k}}\cdots s_{\widetilde{m}_{h,k}+2})(s_{\unicode[STIX]{x1D70E}_{h,k}+2}s_{\unicode[STIX]{x1D70E}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+3})\cdots \\ \displaystyle (s_{\unicode[STIX]{x1D70E}_{h,k}+m_{h+1,k}-1}s_{\unicode[STIX]{x1D70E}_{h,k}+m_{h+1,k}-2}\cdots s_{\widetilde{m}_{h+1,k}}).\end{array}\end{eqnarray}$$
In particular,
![]() $\ell (d_{M_{h,k}^{+}})=\ell (d_{M})+\sum _{j<k}m_{h+1,j}-\sum _{j>k}m_{h,j}$
.
$\ell (d_{M_{h,k}^{+}})=\ell (d_{M})+\sum _{j<k}m_{h+1,j}-\sum _{j>k}m_{h,j}$
.
Remark 3.3. (1) We display the factors
![]() $w_{i,j}$
of
$w_{i,j}$
of
![]() $d_{M}$
through a matrix notation:
$d_{M}$
through a matrix notation:
 $$\begin{eqnarray}\displaystyle d_{M}=\left(\begin{array}{@{}cccc@{}}w_{2,1} & w_{2,2} & \cdots \, & w_{2,n-1}\\ w_{3,1} & w_{3,2} & \cdots \, & w_{3,n-1}\\ \vdots & \vdots & \cdots \, & \vdots \\ w_{n,1} & w_{n,2} & \cdots \, & w_{n,n-1}\end{array}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{M}=\left(\begin{array}{@{}cccc@{}}w_{2,1} & w_{2,2} & \cdots \, & w_{2,n-1}\\ w_{3,1} & w_{3,2} & \cdots \, & w_{3,n-1}\\ \vdots & \vdots & \cdots \, & \vdots \\ w_{n,1} & w_{n,2} & \cdots \, & w_{n,n-1}\end{array}\right), & & \displaystyle\end{eqnarray}$$
where
![]() $d_{M}$
is simply a product of the entries down column 1, then down column 2, and so on. Note that
$d_{M}$
is simply a product of the entries down column 1, then down column 2, and so on. Note that
![]() $w_{i,j}=1$
whenever
$w_{i,j}=1$
whenever
![]() $m_{i,j}=0$
or
$m_{i,j}=0$
or
![]() $m_{i-1,j+1}^{\llcorner }=0$
.
$m_{i-1,j+1}^{\llcorner }=0$
.
(2) Note that a product of the form
![]() $s_{h-1}s_{h-2}\cdots s_{k}$
for
$s_{h-1}s_{h-2}\cdots s_{k}$
for
![]() $h>k$
is in fact the cycle permutation
$h>k$
is in fact the cycle permutation
![]() $h\rightarrow h-1\rightarrow \cdots \rightarrow k+1\rightarrow k\rightarrow h$
. Thus, each
$h\rightarrow h-1\rightarrow \cdots \rightarrow k+1\rightarrow k\rightarrow h$
. Thus, each
![]() $w_{i,j}$
is a product of cycle permutations. Note also that the largest number permuted (or moved) by the partial column product
$w_{i,j}$
is a product of cycle permutations. Note also that the largest number permuted (or moved) by the partial column product
![]() $w_{2,j}w_{3,j}\cdots w_{h,j}$
is
$w_{2,j}w_{3,j}\cdots w_{h,j}$
is
![]() $\unicode[STIX]{x1D70E}_{h-1,j}+m_{h,j}$
.
$\unicode[STIX]{x1D70E}_{h-1,j}+m_{h,j}$
.
Lemma 3.4.
(1) For any nonnegative integers
 $k,i,h$
with
$k,i,h$
with
 $0<k\leqslant i<h<r$
, Hence, for
$0<k\leqslant i<h<r$
, Hence, for $$\begin{eqnarray}s_{i}(s_{h}s_{h-1}\cdots s_{k})=(s_{h}s_{h-1}\cdots s_{k})s_{i+1}.\end{eqnarray}$$
$$\begin{eqnarray}s_{i}(s_{h}s_{h-1}\cdots s_{k})=(s_{h}s_{h-1}\cdots s_{k})s_{i+1}.\end{eqnarray}$$
 $0<k\leqslant i<h_{1}<h_{2}<\cdots <h_{l}<r$
,
$0<k\leqslant i<h_{1}<h_{2}<\cdots <h_{l}<r$
,  $$\begin{eqnarray}\displaystyle & & \displaystyle s_{i}(s_{h_{1}}s_{h_{1}-1}\cdots s_{k})(s_{h_{2}}s_{h_{2}-1}\cdots s_{k+1})\cdots (s_{h_{l}}s_{h_{l}-1}\cdots s_{k+l-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(s_{h_{1}}s_{h_{1}-1}\cdots s_{k})(s_{h_{2}}s_{h_{2}-1}\cdots s_{k+1})\cdots (s_{h_{l}}s_{h_{l}-1}\cdots s_{k+l-1})s_{i+l}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{i}(s_{h_{1}}s_{h_{1}-1}\cdots s_{k})(s_{h_{2}}s_{h_{2}-1}\cdots s_{k+1})\cdots (s_{h_{l}}s_{h_{l}-1}\cdots s_{k+l-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(s_{h_{1}}s_{h_{1}-1}\cdots s_{k})(s_{h_{2}}s_{h_{2}-1}\cdots s_{k+1})\cdots (s_{h_{l}}s_{h_{l}-1}\cdots s_{k+l-1})s_{i+l}.\nonumber\end{eqnarray}$$
(2) With the notation given in (3.0.1) and (3.1.1), if
 $\unicode[STIX]{x1D70E}_{h-1,j}+m_{h,j}<l<\unicode[STIX]{x1D70E}_{h,j}$
and
$\unicode[STIX]{x1D70E}_{h-1,j}+m_{h,j}<l<\unicode[STIX]{x1D70E}_{h,j}$
and
 $l\geqslant \widetilde{m}_{h,j}+1$
, then
$l\geqslant \widetilde{m}_{h,j}+1$
, then  $$\begin{eqnarray}s_{l}(w_{2,j}w_{3,j}\cdots w_{n,j})=(w_{2,j}w_{3,j}\cdots w_{n,j})s_{l+\mathop{\sum }_{i=h+1}^{n}m_{i,j}}.\end{eqnarray}$$
$$\begin{eqnarray}s_{l}(w_{2,j}w_{3,j}\cdots w_{n,j})=(w_{2,j}w_{3,j}\cdots w_{n,j})s_{l+\mathop{\sum }_{i=h+1}^{n}m_{i,j}}.\end{eqnarray}$$
(3) For any
 $1<k\leqslant n$
, if
$1<k\leqslant n$
, if
 $0<x\leqslant m_{h,k}$
and assume
$0<x\leqslant m_{h,k}$
and assume
 $\sum _{j=1}^{k-1}m_{h,j}+x<\unicode[STIX]{x1D706}_{h}$
, then
$\sum _{j=1}^{k-1}m_{h,j}+x<\unicode[STIX]{x1D706}_{h}$
, then  $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h-1,1}+\mathop{\sum }_{j=1}^{k-1}m_{h,j}+x}(w_{2,1}\cdots w_{n,1})\cdots (w_{2,k-1}\cdots w_{n,k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(w_{2,1}\cdots w_{n,1})\cdots (w_{2,k-1}\cdots w_{n,k-1})s_{\unicode[STIX]{x1D70E}_{h-1,k}+x}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h-1,1}+\mathop{\sum }_{j=1}^{k-1}m_{h,j}+x}(w_{2,1}\cdots w_{n,1})\cdots (w_{2,k-1}\cdots w_{n,k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(w_{2,1}\cdots w_{n,1})\cdots (w_{2,k-1}\cdots w_{n,k-1})s_{\unicode[STIX]{x1D70E}_{h-1,k}+x}.\nonumber\end{eqnarray}$$
Proof. The proof for the first two assertions is straightforward. We now prove (3).
Consider the product
![]() $\prod _{t}$
of first
$\prod _{t}$
of first
![]() $t$
columns of
$t$
columns of
![]() $d_{M}$
:
$d_{M}$
:
We claim for all
![]() $t<k$
that
$t<k$
that
Thus, taking
![]() $t=k-1$
gives the assertion (3).
$t=k-1$
gives the assertion (3).
We prove (3.4.1) by induction on
![]() $t$
. If
$t$
. If
![]() $t=1$
, then
$t=1$
, then
![]() $x>0$
implies
$x>0$
implies
As the largest number permuted by
![]() $w_{2,1}\cdots w_{h,1}$
is
$w_{2,1}\cdots w_{h,1}$
is
![]() $\unicode[STIX]{x1D70E}_{h-1,1}+m_{h,1}$
, we have
$\unicode[STIX]{x1D70E}_{h-1,1}+m_{h,1}$
, we have
Now we consider
![]() $s_{l}(w_{h+1,1}\cdots w_{n,1})$
. Assume
$s_{l}(w_{h+1,1}\cdots w_{n,1})$
. Assume
![]() $w_{h+1,1}\neq 1$
(and so
$w_{h+1,1}\neq 1$
(and so
![]() $m_{h+1,1}>0$
). Since
$m_{h+1,1}>0$
). Since
![]() $k>1$
and
$k>1$
and
![]() $\widetilde{m}_{h,1}+1\leqslant l=\unicode[STIX]{x1D70E}_{h-1,1}+\sum _{j=1}^{k-1}m_{h,j}+x<\unicode[STIX]{x1D70E}_{h-1,1}+\unicode[STIX]{x1D706}_{h}=\unicode[STIX]{x1D70E}_{h,1}$
, by (2),
$\widetilde{m}_{h,1}+1\leqslant l=\unicode[STIX]{x1D70E}_{h-1,1}+\sum _{j=1}^{k-1}m_{h,j}+x<\unicode[STIX]{x1D70E}_{h-1,1}+\unicode[STIX]{x1D706}_{h}=\unicode[STIX]{x1D70E}_{h,1}$
, by (2),
![]() $s_{l}w_{h+1,1}=w_{h+1,1}s_{l+m_{h+1,1}}$
and, by an inductive argument as above,
$s_{l}w_{h+1,1}=w_{h+1,1}s_{l+m_{h+1,1}}$
and, by an inductive argument as above,
But
![]() $l+\sum _{i=h+1}^{n}m_{i,1}=\unicode[STIX]{x1D70E}_{h-1,2}+\sum _{j=2}^{k-1}m_{h,j}+x$
. This proves (3.4.1) for
$l+\sum _{i=h+1}^{n}m_{i,1}=\unicode[STIX]{x1D70E}_{h-1,2}+\sum _{j=2}^{k-1}m_{h,j}+x$
. This proves (3.4.1) for
![]() $t=1$
.
$t=1$
.
Suppose now
![]() $t>1$
and (3.4.1) is true for
$t>1$
and (3.4.1) is true for
![]() $t-1$
. That is, assume
$t-1$
. That is, assume
 $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h-1,1}+\mathop{\sum }_{j=1}^{k-1}m_{h,j}+x}(w_{2,1}\cdots w_{n,1})\cdots (w_{2,t-1}\cdots w_{n,t-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(w_{2,1}\cdots w_{n,1})\cdots (w_{2,t-1}\cdots w_{n,t-1})s_{\unicode[STIX]{x1D70E}_{h-1,t}+\mathop{\sum }_{j=t}^{k-1}m_{h,j}+x}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h-1,1}+\mathop{\sum }_{j=1}^{k-1}m_{h,j}+x}(w_{2,1}\cdots w_{n,1})\cdots (w_{2,t-1}\cdots w_{n,t-1})\nonumber\\ \displaystyle & & \displaystyle \quad =(w_{2,1}\cdots w_{n,1})\cdots (w_{2,t-1}\cdots w_{n,t-1})s_{\unicode[STIX]{x1D70E}_{h-1,t}+\mathop{\sum }_{j=t}^{k-1}m_{h,j}+x}.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70E}_{h-1,t}+\sum _{j=t}^{k-1}m_{h,j}+x>\unicode[STIX]{x1D70E}_{h-1,t}+m_{h,t}$
and
$\unicode[STIX]{x1D70E}_{h-1,t}+\sum _{j=t}^{k-1}m_{h,j}+x>\unicode[STIX]{x1D70E}_{h-1,t}+m_{h,t}$
and
applying (2) with
![]() $l=\unicode[STIX]{x1D70E}_{h-1,t}+\sum _{j=t}^{k-1}m_{h,j}+x$
gives
$l=\unicode[STIX]{x1D70E}_{h-1,t}+\sum _{j=t}^{k-1}m_{h,j}+x$
gives
where
 $$\begin{eqnarray}\displaystyle l+\mathop{\sum }_{i=h+1}^{n}m_{i,t} & = & \displaystyle \unicode[STIX]{x1D70E}_{h-1,t}+\mathop{\sum }_{j=t}^{k-1}m_{h,j}+x+\mathop{\sum }_{i=h+1}^{n}m_{i,t}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}_{h-1,t+1}+\mathop{\sum }_{j=t+1}^{k-1}m_{h,j}+x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle l+\mathop{\sum }_{i=h+1}^{n}m_{i,t} & = & \displaystyle \unicode[STIX]{x1D70E}_{h-1,t}+\mathop{\sum }_{j=t}^{k-1}m_{h,j}+x+\mathop{\sum }_{i=h+1}^{n}m_{i,t}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}_{h-1,t+1}+\mathop{\sum }_{j=t+1}^{k-1}m_{h,j}+x.\nonumber\end{eqnarray}$$
This proves (3.4.1) for
![]() $t$
and, hence, (3).
$t$
and, hence, (3).
Corollary 3.5. For
![]() $0<x\leqslant m_{h,k}$
,
$0<x\leqslant m_{h,k}$
,
![]() $l=\unicode[STIX]{x1D70E}_{h-1,1}+\sum _{j=1}^{k-1}m_{h,j}$
with
$l=\unicode[STIX]{x1D70E}_{h-1,1}+\sum _{j=1}^{k-1}m_{h,j}$
with
![]() $l+x<\unicode[STIX]{x1D70E}_{h,1}$
, we have
$l+x<\unicode[STIX]{x1D70E}_{h,1}$
, we have
 $$\begin{eqnarray}\displaystyle s_{l+x}d_{M}=\left(\begin{array}{@{}ccccccc@{}}w_{2,1} & \cdots \, & w_{2,k-1} & w_{2,k} & w_{2,k+1} & \cdots \, & w_{2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \vdots & \cdots \, & \vdots \\ w_{h-1,1} & \cdots \, & w_{h-1,k-1} & w_{h-1,k} & w_{h-1,k+1} & \cdots \, & w_{h-1,n-1}\\ w_{h,1} & \cdots \, & w_{h,k-1} & w_{h,k}^{\ast } & w_{h,k+1} & \cdots \, & w_{h,n-1}\\ w_{h+1,1} & \cdots \, & w_{h+1,k-1} & w_{h+1,k} & w_{h+1,k+1} & \cdots \, & w_{h+1,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \vdots & \cdots \, & \vdots \\ w_{n,1} & \cdots \, & w_{n,k-1} & w_{n,k} & w_{h,k+1} & \cdots \, & w_{n,n-1}\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{l+x}d_{M}=\left(\begin{array}{@{}ccccccc@{}}w_{2,1} & \cdots \, & w_{2,k-1} & w_{2,k} & w_{2,k+1} & \cdots \, & w_{2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \vdots & \cdots \, & \vdots \\ w_{h-1,1} & \cdots \, & w_{h-1,k-1} & w_{h-1,k} & w_{h-1,k+1} & \cdots \, & w_{h-1,n-1}\\ w_{h,1} & \cdots \, & w_{h,k-1} & w_{h,k}^{\ast } & w_{h,k+1} & \cdots \, & w_{h,n-1}\\ w_{h+1,1} & \cdots \, & w_{h+1,k-1} & w_{h+1,k} & w_{h+1,k+1} & \cdots \, & w_{h+1,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \vdots & \cdots \, & \vdots \\ w_{n,1} & \cdots \, & w_{n,k-1} & w_{n,k} & w_{h,k+1} & \cdots \, & w_{n,n-1}\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $w_{h,k}^{\ast }=s_{\unicode[STIX]{x1D70E}_{h-1,k}+x}w_{h,k}$
. In particular,
$w_{h,k}^{\ast }=s_{\unicode[STIX]{x1D70E}_{h-1,k}+x}w_{h,k}$
. In particular,
![]() $s_{l+1}s_{l+2}\cdots s_{l+m_{h,k}}d_{M}$
can be expressed by the same matrix with
$s_{l+1}s_{l+2}\cdots s_{l+m_{h,k}}d_{M}$
can be expressed by the same matrix with
![]() $w_{h,k}^{\ast }=w_{h,k}^{+}$
, the element defined in (3.1.2).
$w_{h,k}^{\ast }=w_{h,k}^{+}$
, the element defined in (3.1.2).
The next result is the key to establish the decomposition in Theorem 3.1 and the multiplication formulas in Theorem 4.1.
Proposition 3.6. Maintain the notation as given in (3.0.1) and Theorem 3.1, and let
![]() $a=\sum _{j=1}^{k-1}m_{h+1,j}$
, and
$a=\sum _{j=1}^{k-1}m_{h+1,j}$
, and
![]() $b=\sum _{j=k+1}^{n}m_{h,j}$
.
$b=\sum _{j=k+1}^{n}m_{h,j}$
.
(1) If
 $m_{h+1,k}\geqslant 1$
then, for
$m_{h+1,k}\geqslant 1$
then, for
 $\unicode[STIX]{x1D706}^{+}=\unicode[STIX]{x1D706}^{[h^{+}]}=\unicode[STIX]{x1D706}+\mathbf{e}_{h}-\mathbf{e}_{h+1}$
and
$\unicode[STIX]{x1D706}^{+}=\unicode[STIX]{x1D706}^{[h^{+}]}=\unicode[STIX]{x1D706}+\mathbf{e}_{h}-\mathbf{e}_{h+1}$
and
 $0\leqslant p<m_{h+1,k}$
,
$0\leqslant p<m_{h+1,k}$
,  $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a+p}d_{M}\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-b}d_{M_{h,k}^{+}}(s_{\widetilde{m}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+p})\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-b+1}d_{M_{h,k}^{+}}(s_{\widetilde{m}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+p}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a+p}d_{M}\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-b}d_{M_{h,k}^{+}}(s_{\widetilde{m}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+p})\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-b+1}d_{M_{h,k}^{+}}(s_{\widetilde{m}_{h,k}+1}\cdots s_{\widetilde{m}_{h,k}+p}).\nonumber\end{eqnarray}$$
(2) If
 $m_{h,k}\geqslant 1$
then, for
$m_{h,k}\geqslant 1$
then, for
 $\unicode[STIX]{x1D706}^{-}=\unicode[STIX]{x1D706}^{[h^{-}]}=\unicode[STIX]{x1D706}-\mathbf{e}_{h}+\mathbf{e}_{h+1}$
and
$\unicode[STIX]{x1D706}^{-}=\unicode[STIX]{x1D706}^{[h^{-}]}=\unicode[STIX]{x1D706}-\mathbf{e}_{h}+\mathbf{e}_{h+1}$
and
 $q=m_{h,k}-p$
with
$q=m_{h,k}-p$
with
 $0<p\leqslant m_{h,k}$
(so
$0<p\leqslant m_{h,k}$
(so
 $0\leqslant q<m_{h,k}$
),
$0\leqslant q<m_{h,k}$
),  $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-b-q}d_{M}\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+a}d_{M_{h,k}^{-}}(s_{\widetilde{m}_{h,k}-1}s_{\widetilde{m}_{h,k}-2}\cdots s_{\widetilde{m}_{h,k}-q})\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a-1}d_{M_{h,k}^{-}}(s_{\widetilde{m}_{h,k}-1}s_{\widetilde{m}_{h,k}-2}\cdots s_{\widetilde{m}_{h,k}-q}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}-b-q}d_{M}\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{-}+a}d_{M_{h,k}^{-}}(s_{\widetilde{m}_{h,k}-1}s_{\widetilde{m}_{h,k}-2}\cdots s_{\widetilde{m}_{h,k}-q})\nonumber\\ \displaystyle & & \displaystyle =s_{\widetilde{\unicode[STIX]{x1D706}}_{h}}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a-1}d_{M_{h,k}^{-}}(s_{\widetilde{m}_{h,k}-1}s_{\widetilde{m}_{h,k}-2}\cdots s_{\widetilde{m}_{h,k}-q}).\nonumber\end{eqnarray}$$
Here every product of the
![]() $s_{i}$
’s is regarded as 1 if its “length” is 0.
$s_{i}$
’s is regarded as 1 if its “length” is 0.
Proof. We only prove (1), (2) follows from (1) with a similar argument. We first assume that
![]() $p=0$
. In this case, we want to prove
$p=0$
. In this case, we want to prove
Since
![]() $a=m_{h+1,1}+\cdots +m_{h+1,k-1}$
, repeatedly applying Corollary 3.5 (with
$a=m_{h+1,1}+\cdots +m_{h+1,k-1}$
, repeatedly applying Corollary 3.5 (with
![]() $h$
replaced by
$h$
replaced by
![]() $h+1$
, noting
$h+1$
, noting
![]() $m_{h+1,k}>0$
) yields
$m_{h+1,k}>0$
) yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a}d_{M}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}cccccc@{}}w_{2,1} & \cdots \, & w_{2,k-1} & w_{2,k} & \cdots \, & w_{2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \cdots \, & \vdots \\ w_{h,1} & \cdots \, & w_{h,k-1} & w_{h,k} & \cdots \, & w_{h,n-1}\\ w_{h+1,1}^{+} & \cdots \, & w_{h+1,k-1}^{+} & w_{h+1,k} & \cdots \, & w_{h+1,n-1}\\ w_{h+2,1} & \cdots \, & w_{h+2,k-1} & w_{h+2,k} & \cdots \, & w_{h+2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \cdots \, & \vdots \\ w_{n,1} & \cdots \, & w_{n,k-1} & w_{n,k} & \cdots \, & w_{n,n-1}\end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+a}d_{M}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}cccccc@{}}w_{2,1} & \cdots \, & w_{2,k-1} & w_{2,k} & \cdots \, & w_{2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \cdots \, & \vdots \\ w_{h,1} & \cdots \, & w_{h,k-1} & w_{h,k} & \cdots \, & w_{h,n-1}\\ w_{h+1,1}^{+} & \cdots \, & w_{h+1,k-1}^{+} & w_{h+1,k} & \cdots \, & w_{h+1,n-1}\\ w_{h+2,1} & \cdots \, & w_{h+2,k-1} & w_{h+2,k} & \cdots \, & w_{h+2,n-1}\\ \vdots & \vdots & \cdots \, & \vdots & \cdots \, & \vdots \\ w_{n,1} & \cdots \, & w_{n,k-1} & w_{n,k} & \cdots \, & w_{n,n-1}\end{array}\right).\nonumber\end{eqnarray}$$
(Note that, if
![]() $k=1$
, then
$k=1$
, then
![]() $a=0$
and so left-hand side (LHS) of (3.6.1)
$a=0$
and so left-hand side (LHS) of (3.6.1)
![]() $=d_{M}$
. Note also that
$=d_{M}$
. Note also that
![]() $w_{h+1,j}^{+}=1$
if
$w_{h+1,j}^{+}=1$
if
![]() $m_{h+1,j}=0$
.) By comparing this with the “matrix” of
$m_{h+1,j}=0$
.) By comparing this with the “matrix” of
![]() $d_{M_{h,k}^{+}}$
, we now show that multiplying
$d_{M_{h,k}^{+}}$
, we now show that multiplying
![]() $d_{M_{h,k}^{+}}$
by
$d_{M_{h,k}^{+}}$
by
![]() $s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-b}$
on the left will turn the product
$s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-b}$
on the left will turn the product
![]() $w_{h,k}^{\bullet }w_{h+1,k}^{\circ }$
into
$w_{h,k}^{\bullet }w_{h+1,k}^{\circ }$
into
![]() $w_{h,k}w_{h+1,k}$
.
$w_{h,k}w_{h+1,k}$
.
If
![]() $b=0$
, then
$b=0$
, then
![]() $\unicode[STIX]{x1D70E}_{h,k}=\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}$
and so
$\unicode[STIX]{x1D70E}_{h,k}=\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}$
and so
![]() $w_{h,k}^{\bullet }w_{h+1,k}^{\circ }=w_{h,k}w_{h+1,k}$
(cf. Lemma 3.2). This proves (3.6.1) in this case. Assume now
$w_{h,k}^{\bullet }w_{h+1,k}^{\circ }=w_{h,k}w_{h+1,k}$
(cf. Lemma 3.2). This proves (3.6.1) in this case. Assume now
![]() $b>0$
. Observe that, for
$b>0$
. Observe that, for
![]() $\unicode[STIX]{x1D706}^{+}=\text{ro}(M_{h,k}^{+})$
,
$\unicode[STIX]{x1D706}^{+}=\text{ro}(M_{h,k}^{+})$
,
![]() $\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\sum _{j>k}m_{h,j}=\widetilde{\unicode[STIX]{x1D706}}_{h-1}+\sum _{j=1}^{k}m_{h,j}+1$
. Let
$\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\sum _{j>k}m_{h,j}=\widetilde{\unicode[STIX]{x1D706}}_{h-1}+\sum _{j=1}^{k}m_{h,j}+1$
. Let
![]() $l=\widetilde{\unicode[STIX]{x1D706}}_{h-1}+\sum _{j=1}^{k-1}m_{h,j}$
and
$l=\widetilde{\unicode[STIX]{x1D706}}_{h-1}+\sum _{j=1}^{k-1}m_{h,j}$
and
![]() $1\leqslant x\leqslant m_{h,k}$
. Then
$1\leqslant x\leqslant m_{h,k}$
. Then
![]() $l+x<l+x+m_{h+1,k}\leqslant \unicode[STIX]{x1D706}_{h+1}$
. By Lemma 3.4(3) (cf. (3.4.1)),
$l+x<l+x+m_{h+1,k}\leqslant \unicode[STIX]{x1D706}_{h+1}$
. By Lemma 3.4(3) (cf. (3.4.1)),
where
![]() $\unicode[STIX]{x1D6F1}_{k-1}^{+}$
is the product of the first
$\unicode[STIX]{x1D6F1}_{k-1}^{+}$
is the product of the first
![]() $k-1$
columns of
$k-1$
columns of
![]() $d_{M_{h,k}^{+}}$
. By (3.3.1) for
$d_{M_{h,k}^{+}}$
. By (3.3.1) for
![]() $M_{h,k}^{+}$
and noting (3.2.1),
$M_{h,k}^{+}$
and noting (3.2.1),
 $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\mathop{\sum }_{j>k}m_{h,j}}d_{M_{h,k}^{+}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F1}_{k-1}^{+}\cdot s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad (w_{2,k}\cdots w_{h-1,k}w_{h,k}^{\bullet }w_{h+1,k}^{\circ }w_{h+2,k}\cdots w_{n,k})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots \nonumber\\ \displaystyle & & \displaystyle \qquad (w_{2,n-1}\cdots w_{h,n-1}w_{h+1,n-1}w_{h+2,n-1}\cdots w_{n,n-1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\mathop{\sum }_{j>k}m_{h,j}}d_{M_{h,k}^{+}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F1}_{k-1}^{+}\cdot s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad (w_{2,k}\cdots w_{h-1,k}w_{h,k}^{\bullet }w_{h+1,k}^{\circ }w_{h+2,k}\cdots w_{n,k})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots \nonumber\\ \displaystyle & & \displaystyle \qquad (w_{2,n-1}\cdots w_{h,n-1}w_{h+1,n-1}w_{h+2,n-1}\cdots w_{n,n-1}).\end{eqnarray}$$
Since the smallest number permuted by
![]() $s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}$
is
$s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}$
is
![]() $\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1$
, while the largest number permuted by
$\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1$
, while the largest number permuted by
![]() $w_{2,1}\cdots w_{h-1,k}w_{h,k}$
is
$w_{2,1}\cdots w_{h-1,k}w_{h,k}$
is
![]() $\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}$
, it follows that
$\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}$
, it follows that
![]() $s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}$
commutes with
$s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}$
commutes with
![]() $w_{2,k}\cdots w_{h-1,k}$
and
$w_{2,k}\cdots w_{h-1,k}$
and
![]() $w_{h,k}$
. Thus,
$w_{h,k}$
. Thus,
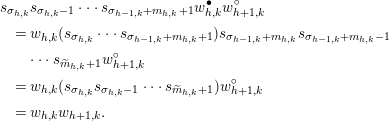 $$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}w_{h,k}^{\bullet }w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h,k}}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1})s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}}s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots s_{\widetilde{m}_{h,k}+1}w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\widetilde{m}_{h,k}+1})w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}w_{h+1,k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1}w_{h,k}^{\bullet }w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h,k}}\cdots s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}+1})s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}}s_{\unicode[STIX]{x1D70E}_{h-1,k}+m_{h,k}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots s_{\widetilde{m}_{h,k}+1}w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}(s_{\unicode[STIX]{x1D70E}_{h,k}}s_{\unicode[STIX]{x1D70E}_{h,k}-1}\cdots s_{\widetilde{m}_{h,k}+1})w_{h+1,k}^{\circ }\nonumber\\ \displaystyle & & \displaystyle \quad =w_{h,k}w_{h+1,k}.\nonumber\end{eqnarray}$$
Hence,
![]() $s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\sum _{j>k}m_{h,j}}d_{M_{h,k}^{+}}=\text{LHS}$
, proving the
$s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}^{+}-\sum _{j>k}m_{h,j}}d_{M_{h,k}^{+}}=\text{LHS}$
, proving the
![]() $p=0$
case.
$p=0$
case.
Assume now
![]() $p>0$
. Then one can easily prove by Corollary 3.5 that
$p>0$
. Then one can easily prove by Corollary 3.5 that
Now the required formula follows from (3.6.1).
Proof of Theorem 3.1.
Set
![]() $D_{h}^{+}=\operatorname{diag}(\unicode[STIX]{x1D706}-\mathbf{e}_{h+1})+E_{h,h+1}$
. Then
$D_{h}^{+}=\operatorname{diag}(\unicode[STIX]{x1D706}-\mathbf{e}_{h+1})+E_{h,h+1}$
. Then
![]() $\text{ro}(D_{h}^{+})=\unicode[STIX]{x1D706}^{[h^{+}]}$
,
$\text{ro}(D_{h}^{+})=\unicode[STIX]{x1D706}^{[h^{+}]}$
,
![]() $\text{co}(D_{h}^{+})=\unicode[STIX]{x1D706}$
, and
$\text{co}(D_{h}^{+})=\unicode[STIX]{x1D706}$
, and
Note that in this case
![]() $d_{D_{h}^{+}}=1$
. Observe that
$d_{D_{h}^{+}}=1$
. Observe that
Putting
![]() $d_{i}=s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+i}$
for
$d_{i}=s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+1}s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+2}\cdots s_{\widetilde{\unicode[STIX]{x1D706}}_{h}+i}$
for
![]() $0\leqslant i\leqslant \unicode[STIX]{x1D706}_{h+1}-1$
, the LHS becomes
$0\leqslant i\leqslant \unicode[STIX]{x1D706}_{h+1}-1$
, the LHS becomes
![]() $\bigcup _{i}W_{\unicode[STIX]{x1D706}^{[h^{+}]}}d_{i}d_{M}W_{\unicode[STIX]{x1D707}}$
. Since
$\bigcup _{i}W_{\unicode[STIX]{x1D706}^{[h^{+}]}}d_{i}d_{M}W_{\unicode[STIX]{x1D707}}$
. Since
![]() $\unicode[STIX]{x1D706}_{h+1}=\sum _{k;m_{h+1,k}\geqslant 1}m_{h+1,k}$
, the first decomposition follows from Proposition 3.6(1). The second decomposition can be proved similarly.
$\unicode[STIX]{x1D706}_{h+1}=\sum _{k;m_{h+1,k}\geqslant 1}m_{h+1,k}$
, the first decomposition follows from Proposition 3.6(1). The second decomposition can be proved similarly.
4 Regular representation of the
 $q$
-Schur superalgebra
$q$
-Schur superalgebra
We now use Proposition 3.6 to derive certain multiplication formulas in
![]() ${\mathcal{S}}(m|n,r)$
and the matrix representation of the regular representation. For any integers
${\mathcal{S}}(m|n,r)$
and the matrix representation of the regular representation. For any integers
![]() $0\leqslant t\leqslant s$
, define Gaussian polynomials in
$0\leqslant t\leqslant s$
, define Gaussian polynomials in
![]() ${\mathcal{Z}}=\mathbb{Z}[\boldsymbol{\unicode[STIX]{x1D710}},\boldsymbol{\unicode[STIX]{x1D710}}^{-1}]$
by
${\mathcal{Z}}=\mathbb{Z}[\boldsymbol{\unicode[STIX]{x1D710}},\boldsymbol{\unicode[STIX]{x1D710}}^{-1}]$
by
where
![]() $\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}^{!}:=\unicode[STIX]{x27E6}1\unicode[STIX]{x27E7}\unicode[STIX]{x27E6}2\unicode[STIX]{x27E7}\cdots \unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}$
with
$\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}^{!}:=\unicode[STIX]{x27E6}1\unicode[STIX]{x27E7}\unicode[STIX]{x27E6}2\unicode[STIX]{x27E7}\cdots \unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}$
with
![]() $\unicode[STIX]{x27E6}i\unicode[STIX]{x27E7}=1+\mathbf{q}+\cdots +\mathbf{q}^{i-1}$
(
$\unicode[STIX]{x27E6}i\unicode[STIX]{x27E7}=1+\mathbf{q}+\cdots +\mathbf{q}^{i-1}$
(
![]() $\mathbf{q}=\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
). Define
$\mathbf{q}=\boldsymbol{\unicode[STIX]{x1D710}}^{2}$
). Define
![]() $[r]^{!}$
similarly with
$[r]^{!}$
similarly with
![]() $[i]=(\boldsymbol{\unicode[STIX]{x1D710}}^{i}-\boldsymbol{\unicode[STIX]{x1D710}}^{-i})/(\boldsymbol{\unicode[STIX]{x1D710}}-\boldsymbol{\unicode[STIX]{x1D710}}^{-1})$
.
$[i]=(\boldsymbol{\unicode[STIX]{x1D710}}^{i}-\boldsymbol{\unicode[STIX]{x1D710}}^{-i})/(\boldsymbol{\unicode[STIX]{x1D710}}-\boldsymbol{\unicode[STIX]{x1D710}}^{-1})$
.
For
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, denote
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, denote
![]() ${\mathcal{P}}_{W_{\unicode[STIX]{x1D706}}}$
to be the super Poincaré polynomial
${\mathcal{P}}_{W_{\unicode[STIX]{x1D706}}}$
to be the super Poincaré polynomial
For
![]() $1\leqslant h\leqslant m+n$
, define
$1\leqslant h\leqslant m+n$
, define
![]() $\dot{\mathbf{q}}_{h},\ddot{\mathbf{q}}_{h},\boldsymbol{\unicode[STIX]{x1D710}}_{h}$
by
$\dot{\mathbf{q}}_{h},\ddot{\mathbf{q}}_{h},\boldsymbol{\unicode[STIX]{x1D710}}_{h}$
by
and let
![]() $\mathbf{q}_{h}=\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{2}$
. Recall the basis
$\mathbf{q}_{h}=\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{2}$
. Recall the basis
![]() $\{{\unicode[STIX]{x1D719}_{A}\}}_{A\in M(m|n,r)}$
given in Lemma 2.1.
$\{{\unicode[STIX]{x1D719}_{A}\}}_{A\in M(m|n,r)}$
given in Lemma 2.1.
Theorem 4.1. For any
![]() $A=(a_{i,j})\in M(m|n,r)$
and
$A=(a_{i,j})\in M(m|n,r)$
and
![]() $1\leqslant h<m+n$
, let
$1\leqslant h<m+n$
, let
![]() $D_{h}^{+},D_{h}^{-}$
be the matrices defined by the conditions that
$D_{h}^{+},D_{h}^{-}$
be the matrices defined by the conditions that
![]() $D_{h}^{+}-E_{h,h+1},D_{h}^{-}-E_{h+1,h}$
are diagonal and
$D_{h}^{+}-E_{h,h+1},D_{h}^{-}-E_{h+1,h}$
are diagonal and
![]() $\text{co}(D_{h}^{+})=\text{co}(D_{h}^{-})=\text{ro}(A)$
, and assume
$\text{co}(D_{h}^{+})=\text{co}(D_{h}^{-})=\text{ro}(A)$
, and assume
![]() $D_{h}^{+},D_{h}^{-}\in M(m|n,r)$
. Then the following multiplication formulas hold in
$D_{h}^{+},D_{h}^{-}\in M(m|n,r)$
. Then the following multiplication formulas hold in
![]() ${\mathcal{S}}(m|n,r)$
:
${\mathcal{S}}(m|n,r)$
:
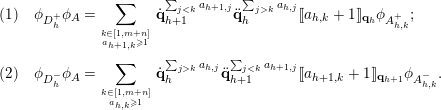 $$\begin{eqnarray}\displaystyle & & \displaystyle (1)\quad \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}\dot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}};\nonumber\\ \displaystyle & & \displaystyle (2)\quad \unicode[STIX]{x1D719}_{D_{h}^{-}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\in [1,m+n]\atop a_{h,k}\geqslant 1}}\dot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\ddot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\unicode[STIX]{x27E6}a_{h+1,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h+1}}\unicode[STIX]{x1D719}_{A_{h,k}^{-}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (1)\quad \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}\dot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}};\nonumber\\ \displaystyle & & \displaystyle (2)\quad \unicode[STIX]{x1D719}_{D_{h}^{-}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\in [1,m+n]\atop a_{h,k}\geqslant 1}}\dot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\ddot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\unicode[STIX]{x27E6}a_{h+1,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h+1}}\unicode[STIX]{x1D719}_{A_{h,k}^{-}}.\nonumber\end{eqnarray}$$
(Here
![]() $[1,m+n]=\{1,2,\ldots ,m+n\}$
.)
$[1,m+n]=\{1,2,\ldots ,m+n\}$
.)
Proof. We only prove (1). The proof of (2) is symmetric.
Let
![]() $\unicode[STIX]{x1D706}=\text{ro}(A)$
,
$\unicode[STIX]{x1D706}=\text{ro}(A)$
,
![]() $\unicode[STIX]{x1D707}=\text{co}(A)$
,
$\unicode[STIX]{x1D707}=\text{co}(A)$
,
![]() $d=d_{A}$
and
$d=d_{A}$
and
![]() $W_{\unicode[STIX]{x1D708}}=W_{\unicode[STIX]{x1D706}}^{d}\cap W_{\unicode[STIX]{x1D707}}=W_{\unicode[STIX]{x1D708}^{(0)}}\times W_{\unicode[STIX]{x1D708}^{(1)}}$
(cf. (3.0.1)), where
$W_{\unicode[STIX]{x1D708}}=W_{\unicode[STIX]{x1D706}}^{d}\cap W_{\unicode[STIX]{x1D707}}=W_{\unicode[STIX]{x1D708}^{(0)}}\times W_{\unicode[STIX]{x1D708}^{(1)}}$
(cf. (3.0.1)), where
![]() $W_{\unicode[STIX]{x1D708}^{(i)}}=W_{\unicode[STIX]{x1D706}^{(i)}}^{d}\cap W_{\unicode[STIX]{x1D707}^{(i)}}$
for
$W_{\unicode[STIX]{x1D708}^{(i)}}=W_{\unicode[STIX]{x1D706}^{(i)}}^{d}\cap W_{\unicode[STIX]{x1D707}^{(i)}}$
for
![]() $i=0,1$
. Then
$i=0,1$
. Then
![]() $\unicode[STIX]{x1D706}=\text{co}(D_{h}^{+})$
,
$\unicode[STIX]{x1D706}=\text{co}(D_{h}^{+})$
,
![]() $\unicode[STIX]{x1D706}^{[h^{+}]}=\text{ro}(D_{h}^{+})=\unicode[STIX]{x1D706}+\mathbf{e}_{h}-\mathbf{e}_{h+1}$
, and
$\unicode[STIX]{x1D706}^{[h^{+}]}=\text{ro}(D_{h}^{+})=\unicode[STIX]{x1D706}+\mathbf{e}_{h}-\mathbf{e}_{h+1}$
, and
![]() $\jmath (\unicode[STIX]{x1D706}^{[h^{+}]},1,\unicode[STIX]{x1D706})=D_{h}^{+}$
.
$\jmath (\unicode[STIX]{x1D706}^{[h^{+}]},1,\unicode[STIX]{x1D706})=D_{h}^{+}$
.
Putting
![]() $W_{\unicode[STIX]{x1D708}^{\prime }(h)}=W_{\unicode[STIX]{x1D706}^{[h^{+}]}}\cap W_{\unicode[STIX]{x1D706}}$
, we see from (3.6.4),
$W_{\unicode[STIX]{x1D708}^{\prime }(h)}=W_{\unicode[STIX]{x1D706}^{[h^{+}]}}\cap W_{\unicode[STIX]{x1D706}}$
, we see from (3.6.4),
Since
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}\subseteq W_{\unicode[STIX]{x1D706}^{(1)}}$
whenever
${\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}\subseteq W_{\unicode[STIX]{x1D706}^{(1)}}$
whenever
![]() $h\geqslant m$
, the element
$h\geqslant m$
, the element
![]() $T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}$
used in (2.0.12) can be written as
$T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}$
used in (2.0.12) can be written as
![]() $T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}=\sum _{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}(\dot{\mathbf{q}}_{h+1})^{\ell (w)}T_{w}$
.
$T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}=\sum _{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}(\dot{\mathbf{q}}_{h+1})^{\ell (w)}T_{w}$
.
By definition, to compute
![]() $\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}$
, it suffices to write
$\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}$
, it suffices to write
![]() $\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}})$
as a linear combination of some
$\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}})$
as a linear combination of some
![]() $T_{W_{\unicode[STIX]{x1D709}}d^{\prime }W_{\unicode[STIX]{x1D707}}}$
, where
$T_{W_{\unicode[STIX]{x1D709}}d^{\prime }W_{\unicode[STIX]{x1D707}}}$
, where
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}^{[h^{+}]}$
. We compute this within
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}^{[h^{+}]}$
. We compute this within
![]() ${\mathcal{S}}_{\mathbb{Q}(\boldsymbol{\unicode[STIX]{x1D710}})}(m|n,r)$
:
${\mathcal{S}}_{\mathbb{Q}(\boldsymbol{\unicode[STIX]{x1D710}})}(m|n,r)$
:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{d}([xy]_{\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}(T_{W_{\unicode[STIX]{x1D706}}dW_{\unicode[STIX]{x1D707}}})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}([xy]_{\unicode[STIX]{x1D706}}T_{d}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}}\cap W_{\unicode[STIX]{x1D707}}})~\text{(by (2.0.12))}\nonumber\\ \displaystyle & = & \displaystyle T_{W_{\unicode[STIX]{x1D709}}W_{\unicode[STIX]{x1D706}}}T_{d}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}}\cap W_{\unicode[STIX]{x1D707}}}=({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}T_{W_{\unicode[STIX]{x1D709}}W_{\unicode[STIX]{x1D706}}}T_{d}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle ({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}[xy]_{\unicode[STIX]{x1D709}}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}T_{d}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle ({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}\mathop{\sum }_{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}[xy]_{\unicode[STIX]{x1D709}}({\dot{\mathbf{q}}_{h+1}}^{\ell (w)}T_{w})T_{d}[xy]_{\unicode[STIX]{x1D707}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}}) & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{d}([xy]_{\unicode[STIX]{x1D707}})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}(T_{W_{\unicode[STIX]{x1D706}}dW_{\unicode[STIX]{x1D707}}})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D706}}^{1}([xy]_{\unicode[STIX]{x1D706}}T_{d}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}}\cap W_{\unicode[STIX]{x1D707}}})~\text{(by (2.0.12))}\nonumber\\ \displaystyle & = & \displaystyle T_{W_{\unicode[STIX]{x1D709}}W_{\unicode[STIX]{x1D706}}}T_{d}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}}\cap W_{\unicode[STIX]{x1D707}}}=({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}T_{W_{\unicode[STIX]{x1D709}}W_{\unicode[STIX]{x1D706}}}T_{d}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle ({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}[xy]_{\unicode[STIX]{x1D709}}T_{{\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}T_{d}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle ({\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}})^{-1}\mathop{\sum }_{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }(h)}\cap W_{\unicode[STIX]{x1D706}}}[xy]_{\unicode[STIX]{x1D709}}({\dot{\mathbf{q}}_{h+1}}^{\ell (w)}T_{w})T_{d}[xy]_{\unicode[STIX]{x1D707}}.\end{eqnarray}$$
Note that
![]() $d=d_{A}\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
. If
$d=d_{A}\in {\mathcal{D}}_{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}}$
. If
![]() $a_{h+1,k}>0$
and
$a_{h+1,k}>0$
and
for some
![]() $0\leqslant p<a_{h+1,k}$
, then by Proposition 3.6(1), we have
$0\leqslant p<a_{h+1,k}$
, then by Proposition 3.6(1), we have
where
![]() $d^{+}=d_{A_{h,k}^{+}}$
. Clearly,
$d^{+}=d_{A_{h,k}^{+}}$
. Clearly,
![]() $\sum _{j<k}a_{h+1,j}=\ell (w_{p})-p$
. If we put
$\sum _{j<k}a_{h+1,j}=\ell (w_{p})-p$
. If we put
![]() $Q_{h+1,k}=\dot{\mathbf{q}}_{h+1}^{\sum _{j<k}a_{h+1,j}}$
, then
$Q_{h+1,k}=\dot{\mathbf{q}}_{h+1}^{\sum _{j<k}a_{h+1,j}}$
, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p=0}^{a_{h+1,k}-1}{\dot{\mathbf{q}}_{h+1}}^{\ell (w_{p})}T_{w_{p}}T_{d}=Q_{h+1,k}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-\mathop{\sum }_{j>k}a_{h,j}+1}T_{d^{+}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot (1+\dot{\mathbf{q}}_{h+1}T_{\widetilde{a}_{h,k}+1}+\cdots +\dot{\mathbf{q}}_{h+1}^{a_{h+1,k}-1}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p=0}^{a_{h+1,k}-1}{\dot{\mathbf{q}}_{h+1}}^{\ell (w_{p})}T_{w_{p}}T_{d}=Q_{h+1,k}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-\mathop{\sum }_{j>k}a_{h,j}+1}T_{d^{+}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot (1+\dot{\mathbf{q}}_{h+1}T_{\widetilde{a}_{h,k}+1}+\cdots +\dot{\mathbf{q}}_{h+1}^{a_{h+1,k}-1}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1}).\nonumber\end{eqnarray}$$
Thus,
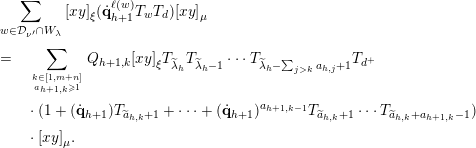 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }}\cap W_{\unicode[STIX]{x1D706}}}[xy]_{\unicode[STIX]{x1D709}}(\dot{\mathbf{q}}_{h+1}^{\ell (w)}T_{w}T_{d})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle =\quad \mathop{\sum }_{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}Q_{h+1,k}[xy]_{\unicode[STIX]{x1D709}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-\mathop{\sum }_{j>k}a_{h,j}+1}T_{d^{+}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(1+(\dot{\mathbf{q}}_{h+1})T_{\widetilde{a}_{h,k}+1}+\cdots +(\dot{\mathbf{q}}_{h+1})^{a_{h+1,k-1}}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,[xy]_{\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{w\in {\mathcal{D}}_{\unicode[STIX]{x1D708}^{\prime }}\cap W_{\unicode[STIX]{x1D706}}}[xy]_{\unicode[STIX]{x1D709}}(\dot{\mathbf{q}}_{h+1}^{\ell (w)}T_{w}T_{d})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle =\quad \mathop{\sum }_{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}Q_{h+1,k}[xy]_{\unicode[STIX]{x1D709}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}}T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-1}\cdots T_{\widetilde{\unicode[STIX]{x1D706}}_{h}-\mathop{\sum }_{j>k}a_{h,j}+1}T_{d^{+}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(1+(\dot{\mathbf{q}}_{h+1})T_{\widetilde{a}_{h,k}+1}+\cdots +(\dot{\mathbf{q}}_{h+1})^{a_{h+1,k-1}}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,[xy]_{\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$
Since
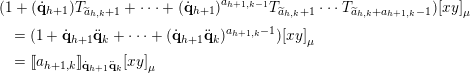 $$\begin{eqnarray}\displaystyle & & \displaystyle (1+(\dot{\mathbf{q}}_{h+1})T_{\widetilde{a}_{h,k}+1}+\cdots +(\dot{\mathbf{q}}_{h+1})^{a_{h+1,k-1}}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle \quad =(1+\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}+\cdots +(\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k})^{a_{h+1,k}-1})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}[xy]_{\unicode[STIX]{x1D707}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (1+(\dot{\mathbf{q}}_{h+1})T_{\widetilde{a}_{h,k}+1}+\cdots +(\dot{\mathbf{q}}_{h+1})^{a_{h+1,k-1}}T_{\widetilde{a}_{h,k}+1}\cdots T_{\widetilde{a}_{h,k}+a_{h+1,k}-1})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle \quad =(1+\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}+\cdots +(\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k})^{a_{h+1,k}-1})[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}[xy]_{\unicode[STIX]{x1D707}}\nonumber\end{eqnarray}$$
and
it follows that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}}) & = & \displaystyle {\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}^{-1}\mathop{\sum }_{a_{h+1,k}\geqslant 1}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}[xy]_{\unicode[STIX]{x1D709}}T_{d^{+}}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{a_{h+1,k}\geqslant 1}\frac{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}^{\prime \prime }}}}{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}T_{W_{\unicode[STIX]{x1D709}}d^{+}W_{\unicode[STIX]{x1D707}}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{a_{h+1,k}\geqslant 1}\frac{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}^{\prime \prime }}}}{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}}([xy]_{\unicode[STIX]{x1D707}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}([xy]_{\unicode[STIX]{x1D707}}) & = & \displaystyle {\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}^{-1}\mathop{\sum }_{a_{h+1,k}\geqslant 1}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}[xy]_{\unicode[STIX]{x1D709}}T_{d^{+}}[xy]_{\unicode[STIX]{x1D707}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{a_{h+1,k}\geqslant 1}\frac{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}^{\prime \prime }}}}{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}T_{W_{\unicode[STIX]{x1D709}}d^{+}W_{\unicode[STIX]{x1D707}}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{a_{h+1,k}\geqslant 1}\frac{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}^{\prime \prime }}}}{{\mathcal{P}}_{W_{\unicode[STIX]{x1D708}}}}Q_{h+1,k}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}}([xy]_{\unicode[STIX]{x1D707}}),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D708}^{\prime \prime }=\unicode[STIX]{x1D708}_{M}$
with
$\unicode[STIX]{x1D708}^{\prime \prime }=\unicode[STIX]{x1D708}_{M}$
with
![]() $M=A_{h,k}^{+}$
or
$M=A_{h,k}^{+}$
or
![]() $W_{\unicode[STIX]{x1D708}^{\prime \prime }}=W_{\unicode[STIX]{x1D709}}^{d^{+}}\cap W_{\unicode[STIX]{x1D707}}$
. Hence, noting
$W_{\unicode[STIX]{x1D708}^{\prime \prime }}=W_{\unicode[STIX]{x1D709}}^{d^{+}}\cap W_{\unicode[STIX]{x1D707}}$
. Hence, noting
we obtain
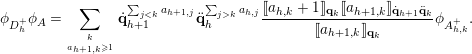 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\atop a_{h+1,k}\geqslant 1}}\dot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\frac{\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}}{\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{D_{h}^{+}}\unicode[STIX]{x1D719}_{A}=\mathop{\sum }_{{k\atop a_{h+1,k}\geqslant 1}}\dot{\mathbf{q}}_{h+1}^{\mathop{\sum }_{j<k}a_{h+1,j}}\ddot{\mathbf{q}}_{h}^{\mathop{\sum }_{j>k}a_{h,j}}\frac{\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}}{\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}}\unicode[STIX]{x1D719}_{A_{h,k}^{+}}.\end{eqnarray}$$
It remains to prove that
This can be seen in cases. For example, if
![]() $h<m$
and
$h<m$
and
![]() $k\leqslant m$
(resp.,
$k\leqslant m$
(resp.,
![]() $h>m$
and
$h>m$
and
![]() $k>m$
), then
$k>m$
), then
![]() $\dot{\mathbf{q}}_{h+1}=1$
,
$\dot{\mathbf{q}}_{h+1}=1$
,
![]() $\ddot{\mathbf{q}}_{k}=\mathbf{q}$
(resp.,
$\ddot{\mathbf{q}}_{k}=\mathbf{q}$
(resp.,
![]() $\dot{\mathbf{q}}_{h+1}=-\mathbf{q}^{-1}$
,
$\dot{\mathbf{q}}_{h+1}=-\mathbf{q}^{-1}$
,
![]() $\ddot{\mathbf{q}}_{k}=-1$
), and so
$\ddot{\mathbf{q}}_{k}=-1$
), and so
![]() $\mathbf{q}_{k}=\mathbf{q}_{h}$
(resp.,
$\mathbf{q}_{k}=\mathbf{q}_{h}$
(resp.,
![]() $\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}=\mathbf{q}_{h}$
). Hence,
$\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}=\mathbf{q}_{h}$
). Hence,
When
![]() $h\leqslant m$
and
$h\leqslant m$
and
![]() $k>m$
, or
$k>m$
, or
![]() $h>m$
and
$h>m$
and
![]() $k\leqslant m$
, we must have
$k\leqslant m$
, we must have
![]() $a_{h,k}+1=a_{h+1,k}=1$
. Thus,
$a_{h,k}+1=a_{h+1,k}=1$
. Thus,
![]() $\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}=\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=1=\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h}}$
. Finally, when
$\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}=\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=1=\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}_{\mathbf{q}_{h}}$
. Finally, when
![]() $h=m$
and
$h=m$
and
![]() $k\leqslant m$
, we have
$k\leqslant m$
, we have
![]() $\mathbf{q}_{h}=\mathbf{q}_{k}$
and
$\mathbf{q}_{h}=\mathbf{q}_{k}$
and
![]() $\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}=-\mathbf{q}^{-1}\mathbf{q}=-1$
. But
$\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}=-\mathbf{q}^{-1}\mathbf{q}=-1$
. But
![]() $a_{h+1,k}=a_{m+1,k}=1$
, forcing
$a_{h+1,k}=a_{m+1,k}=1$
, forcing
![]() $\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}=\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=1$
. Hence,
$\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\dot{\mathbf{q}}_{h+1}\ddot{\mathbf{q}}_{k}}=\unicode[STIX]{x27E6}a_{h+1,k}\unicode[STIX]{x27E7}_{\mathbf{q}_{k}}=1$
. Hence,
proving (4.1.3) and, hence, formula (1).
If
![]() $n=0$
, then
$n=0$
, then
![]() ${\mathcal{S}}(m|0,r)$
is the usual
${\mathcal{S}}(m|0,r)$
is the usual
![]() $\mathbf{q}$
-Schur algebra, which is defined in [Reference Beilinson, Lusztig and MacPherson1] as a convolution algebra of the
$\mathbf{q}$
-Schur algebra, which is defined in [Reference Beilinson, Lusztig and MacPherson1] as a convolution algebra of the
![]() $m$
-step flags of an
$m$
-step flags of an
![]() $r$
-dimensional space. Similar multiplication formulas are obtained in [Reference Beilinson, Lusztig and MacPherson1, Lemma 3.4] by counting intersections of certain orbits. Observe that, for
$r$
-dimensional space. Similar multiplication formulas are obtained in [Reference Beilinson, Lusztig and MacPherson1, Lemma 3.4] by counting intersections of certain orbits. Observe that, for
![]() $h<m$
,
$h<m$
,
Corollary 4.2. The multiplication formulas in Theorem 4.1 for
![]() ${\mathcal{S}}(m|0,r)$
coincide with the ones in [Reference Beilinson, Lusztig and MacPherson1, Lemma 3.4].
${\mathcal{S}}(m|0,r)$
coincide with the ones in [Reference Beilinson, Lusztig and MacPherson1, Lemma 3.4].
We now make a comparison of these new formulas with ones given in [Reference Du and Gu12, Lemma 3.1], derived through the relative norm method.
The
![]() ${\mathcal{H}}$
-module
${\mathcal{H}}$
-module
![]() $\mathfrak{T}(m|n,r)$
is isomorphic to the tensor superspace
$\mathfrak{T}(m|n,r)$
is isomorphic to the tensor superspace
![]() $V(m|n)^{\otimes r}$
(over
$V(m|n)^{\otimes r}$
(over
![]() ${\mathcal{Z}}$
!) with an
${\mathcal{Z}}$
!) with an
![]() ${\mathcal{H}}$
-action defined in [Reference Du and Gu12, (1.0.10)]; see [Reference Du and Rui16, Proposition 8.3]. In fact, the endomorphism algebra of
${\mathcal{H}}$
-action defined in [Reference Du and Gu12, (1.0.10)]; see [Reference Du and Rui16, Proposition 8.3]. In fact, the endomorphism algebra of
![]() $V(m|n)^{\otimes r}$
has a relative norm basis
$V(m|n)^{\otimes r}$
has a relative norm basis
![]() $\{{N_{A}\}}_{A\in M(m|n,r)}$
acting on the right. Matrix transposing may turn the right action to a left action and result in a basis denoted by
$\{{N_{A}\}}_{A\in M(m|n,r)}$
acting on the right. Matrix transposing may turn the right action to a left action and result in a basis denoted by
![]() $\{{\unicode[STIX]{x1D701}_{A}\}}_{A\in M(m|n,r)}$
. The
$\{{\unicode[STIX]{x1D701}_{A}\}}_{A\in M(m|n,r)}$
. The
![]() ${\mathcal{H}}$
-module isomorphism induces an algebra isomorphism (cf. [Reference Du and Rui16, Corollary 8.4] and [Reference Du and Gu13, Lemma 2.3])
${\mathcal{H}}$
-module isomorphism induces an algebra isomorphism (cf. [Reference Du and Rui16, Corollary 8.4] and [Reference Du and Gu13, Lemma 2.3])
where
![]() $\widehat{A}=\sum _{m<k<i\leqslant m+n,1\leqslant j<l\leqslant m+n}a_{i,j}a_{k,l}$
.
$\widehat{A}=\sum _{m<k<i\leqslant m+n,1\leqslant j<l\leqslant m+n}a_{i,j}a_{k,l}$
.
Corollary 4.3. Let
Then
 $$\begin{eqnarray}\displaystyle (-1)^{\widehat{D}_{h}^{+}+\widehat{A}+\widehat{A}_{h,k}^{+}}f_{h,k}^{+}(\mathbf{q},A) & = & \displaystyle f_{k}(\mathbf{q},A,h)\quad \text{and}\nonumber\\ \displaystyle (-1)^{\widehat{D}_{h}^{-}+\widehat{A}+\widehat{A}_{h,k}^{-}}f_{h,k}^{-}(\mathbf{q},A) & = & \displaystyle g_{k}(\mathbf{q},A,h),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (-1)^{\widehat{D}_{h}^{+}+\widehat{A}+\widehat{A}_{h,k}^{+}}f_{h,k}^{+}(\mathbf{q},A) & = & \displaystyle f_{k}(\mathbf{q},A,h)\quad \text{and}\nonumber\\ \displaystyle (-1)^{\widehat{D}_{h}^{-}+\widehat{A}+\widehat{A}_{h,k}^{-}}f_{h,k}^{-}(\mathbf{q},A) & = & \displaystyle g_{k}(\mathbf{q},A,h),\nonumber\end{eqnarray}$$
where
![]() $f_{k}(\mathbf{q},A,h)$
and
$f_{k}(\mathbf{q},A,h)$
and
![]() $g_{k}(\mathbf{q},A,h)$
are defined in [Reference Du and Gu12, (3.0.1-2)]. In particular, rewriting the multiplication formulas in Theorem 4.1 in terms of the
$g_{k}(\mathbf{q},A,h)$
are defined in [Reference Du and Gu12, (3.0.1-2)]. In particular, rewriting the multiplication formulas in Theorem 4.1 in terms of the
![]() $\unicode[STIX]{x1D701}$
-basis results in the formulas in [Reference Du and Gu12, Lemma 3.1].
$\unicode[STIX]{x1D701}$
-basis results in the formulas in [Reference Du and Gu12, Lemma 3.1].
Proof. We have
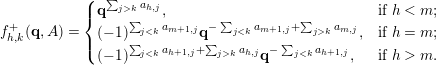 $$\begin{eqnarray}f_{h,k}^{+}(\mathbf{q},A)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathbf{q}^{\mathop{\sum }_{j>k}a_{h,j}},\quad & \text{if }h<m;\\ \displaystyle (-1)^{\mathop{\sum }_{j<k}a_{m+1,j}}\mathbf{q}^{-\mathop{\sum }_{j<k}a_{m+1,j}+\mathop{\sum }_{j>k}a_{m,j}},\quad & \text{if }h=m;\\ \displaystyle (-1)^{\mathop{\sum }_{j<k}a_{h+1,j}+\mathop{\sum }_{j>k}a_{h,j}}\mathbf{q}^{-\mathop{\sum }_{j<k}a_{h+1,j}},\quad & \text{if }h>m.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{h,k}^{+}(\mathbf{q},A)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathbf{q}^{\mathop{\sum }_{j>k}a_{h,j}},\quad & \text{if }h<m;\\ \displaystyle (-1)^{\mathop{\sum }_{j<k}a_{m+1,j}}\mathbf{q}^{-\mathop{\sum }_{j<k}a_{m+1,j}+\mathop{\sum }_{j>k}a_{m,j}},\quad & \text{if }h=m;\\ \displaystyle (-1)^{\mathop{\sum }_{j<k}a_{h+1,j}+\mathop{\sum }_{j>k}a_{h,j}}\mathbf{q}^{-\mathop{\sum }_{j<k}a_{h+1,j}},\quad & \text{if }h>m.\end{array}\right.\end{eqnarray}$$
On the other hand (cf. [Reference Du and Gu12, Lemma 5.1]), for the choice of
![]() $+$
or
$+$
or
![]() $-$
,
$-$
,
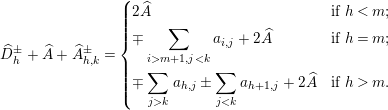 $$\begin{eqnarray}\displaystyle \widehat{D}_{h}^{\pm }+\widehat{A}+\widehat{A}_{h,k}^{\pm }=\left\{\begin{array}{@{}ll@{}}\displaystyle 2\widehat{A} & \text{if }h<m;\\ \displaystyle \mp \mathop{\sum }_{i>m+1,j<k}a_{i,j}+2\widehat{A} & \text{if }h=m;\\ \displaystyle \mp \mathop{\sum }_{j>k}a_{h,j}\pm \mathop{\sum }_{j<k}a_{h+1,j}+2\widehat{A} & \text{if }h>m.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{D}_{h}^{\pm }+\widehat{A}+\widehat{A}_{h,k}^{\pm }=\left\{\begin{array}{@{}ll@{}}\displaystyle 2\widehat{A} & \text{if }h<m;\\ \displaystyle \mp \mathop{\sum }_{i>m+1,j<k}a_{i,j}+2\widehat{A} & \text{if }h=m;\\ \displaystyle \mp \mathop{\sum }_{j>k}a_{h,j}\pm \mathop{\sum }_{j<k}a_{h+1,j}+2\widehat{A} & \text{if }h>m.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Adjusting the right-hand side of (4.3.1) by the corresponding sign for the “
![]() $+$
” case gives
$+$
” case gives
![]() $f_{k}(\mathbf{q},A,h)$
. The “
$f_{k}(\mathbf{q},A,h)$
. The “
![]() $-$
” case is similar.
$-$
” case is similar.
Theorem 4.1 and Corollary 4.3 give a new method to derive the key fundamental multiplication formulas given in [Reference Du and Gu12, Lemma 3.1].
By introducing the normalized basis
![]() $\{[A]\}_{A\in M(m|n,r)}$
, whereFootnote
1
$\{[A]\}_{A\in M(m|n,r)}$
, whereFootnote
1
we may modify the formulas given in Theorem 4.1 to obtain further multiplication formulas for the
![]() $[~]$
-basis; cf. (the
$[~]$
-basis; cf. (the
![]() $p=1$
case of) [Reference Du and Gu12, Propositions 4.4 and 4.5].
$p=1$
case of) [Reference Du and Gu12, Propositions 4.4 and 4.5].
Corollary 4.4. Maintain the notation above and let
![]() $\unicode[STIX]{x1D716}_{h,k}=0$
for
$\unicode[STIX]{x1D716}_{h,k}=0$
for
![]() $h\neq m$
, and
$h\neq m$
, and
![]() $\unicode[STIX]{x1D716}_{m,k}=\sum _{i>m,j<k}a_{i,j}$
. The following multiplication formulas hold in
$\unicode[STIX]{x1D716}_{m,k}=\sum _{i>m,j<k}a_{i,j}$
. The following multiplication formulas hold in
![]() ${\mathcal{S}}_{R}(m|n,r)$
:
${\mathcal{S}}_{R}(m|n,r)$
:
(1)
 $[D_{h}^{+}][A]=\displaystyle \sum _{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}(-1)^{\unicode[STIX]{x1D716}_{h,k}}\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{f_{h,k}^{+}}\overline{\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}}_{\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{2}}[A_{h,k}^{+}]$
, where
$[D_{h}^{+}][A]=\displaystyle \sum _{{k\in [1,m+n]\atop a_{h+1,k}\geqslant 1}}(-1)^{\unicode[STIX]{x1D716}_{h,k}}\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{f_{h,k}^{+}}\overline{\unicode[STIX]{x27E6}a_{h,k}+1\unicode[STIX]{x27E7}}_{\boldsymbol{\unicode[STIX]{x1D710}}_{h}^{2}}[A_{h,k}^{+}]$
, where
 $f_{h,k}^{+}=\sum _{j\geqslant k}a_{h,j}-(-1)^{\widehat{h}+\widehat{h+1}}\sum _{j>k}a_{h+1,j}$
;
$f_{h,k}^{+}=\sum _{j\geqslant k}a_{h,j}-(-1)^{\widehat{h}+\widehat{h+1}}\sum _{j>k}a_{h+1,j}$
;(2)
 $[D_{h}^{-}][A]=\displaystyle \sum _{{k\in [1,m+n]\atop a_{h,k}\geqslant 1}}(-1)^{\unicode[STIX]{x1D716}_{h,k}}\boldsymbol{\unicode[STIX]{x1D710}}_{h+1}^{f_{h,k}^{-}}\overline{\unicode[STIX]{x27E6}a_{h+1,k}+1\unicode[STIX]{x27E7}}_{\boldsymbol{\unicode[STIX]{x1D710}}_{h+1}^{2}}[A_{h,k}^{-}]$
, where
$[D_{h}^{-}][A]=\displaystyle \sum _{{k\in [1,m+n]\atop a_{h,k}\geqslant 1}}(-1)^{\unicode[STIX]{x1D716}_{h,k}}\boldsymbol{\unicode[STIX]{x1D710}}_{h+1}^{f_{h,k}^{-}}\overline{\unicode[STIX]{x27E6}a_{h+1,k}+1\unicode[STIX]{x27E7}}_{\boldsymbol{\unicode[STIX]{x1D710}}_{h+1}^{2}}[A_{h,k}^{-}]$
, where
 $f_{h,k}^{-}=\sum _{j\leqslant k}a_{h+1,j}-(-1)^{\widehat{h}+\widehat{h+1}}\sum _{j<k}a_{h,j}$
.
$f_{h,k}^{-}=\sum _{j\leqslant k}a_{h+1,j}-(-1)^{\widehat{h}+\widehat{h+1}}\sum _{j<k}a_{h,j}$
.
The first important application of the multiplication formulas above is a new realization of the quantum supergroup
![]() $\mathbf{U}_{\boldsymbol{\unicode[STIX]{x1D710}}}(\mathfrak{g}\mathfrak{l}_{m|n})$
; see the argument from [Reference Du and Gu12, Section 5] onwards and, in particular, see [Reference Du and Gu12, Definition 6.1, Theorem 8.4].
$\mathbf{U}_{\boldsymbol{\unicode[STIX]{x1D710}}}(\mathfrak{g}\mathfrak{l}_{m|n})$
; see the argument from [Reference Du and Gu12, Section 5] onwards and, in particular, see [Reference Du and Gu12, Definition 6.1, Theorem 8.4].
We now seek further applications of these multiplication formulas.
We will show below that the formulas provide enough information for the regular representation of the integral
![]() $q$
-Schur superalgebra
$q$
-Schur superalgebra
![]() ${\mathcal{S}}_{R}(m|n,r)$
. We then use such a representation to determine the semisimplicity of
${\mathcal{S}}_{R}(m|n,r)$
. We then use such a representation to determine the semisimplicity of
![]() $q$
-Schur superalgebras and to construct infinitesimal and little ones without involving the quantum supergroup or quantum coordinate superalgebra.
$q$
-Schur superalgebras and to construct infinitesimal and little ones without involving the quantum supergroup or quantum coordinate superalgebra.
We return to the general setting for
![]() ${\mathcal{S}}_{R}(m|n,r)$
defined relative to a commutative ring
${\mathcal{S}}_{R}(m|n,r)$
defined relative to a commutative ring
![]() $R$
and an invertible parameter
$R$
and an invertible parameter
![]() $\unicode[STIX]{x1D710}\in R$
or
$\unicode[STIX]{x1D710}\in R$
or
![]() $q=\unicode[STIX]{x1D710}^{2}$
. Base change via
$q=\unicode[STIX]{x1D710}^{2}$
. Base change via
![]() ${\mathcal{Z}}\rightarrow R,\boldsymbol{\unicode[STIX]{x1D710}}\mapsto \unicode[STIX]{x1D710}$
, we may turn the multiplication formulas in
${\mathcal{Z}}\rightarrow R,\boldsymbol{\unicode[STIX]{x1D710}}\mapsto \unicode[STIX]{x1D710}$
, we may turn the multiplication formulas in
![]() ${\mathcal{S}}(m|n,r)$
into similar formulas in
${\mathcal{S}}(m|n,r)$
into similar formulas in
![]() ${\mathcal{S}}_{R}(m|n,r)$
. In fact, these formulas can be interpreted as the matrix representation of certain generators for
${\mathcal{S}}_{R}(m|n,r)$
. In fact, these formulas can be interpreted as the matrix representation of certain generators for
![]() ${\mathcal{S}}_{R}(m|n,r)$
relative to the basis
${\mathcal{S}}_{R}(m|n,r)$
relative to the basis
![]() $\{[A]\}_{A\in M(m|n,r)}$
.
$\{[A]\}_{A\in M(m|n,r)}$
.
Let
For
![]() $A\in M(m|n)^{\pm }$
and
$A\in M(m|n)^{\pm }$
and
![]() $\mathbf{j}=(j_{1},j_{2},\ldots ,j_{m+n})\in \mathbb{Z}^{m+n}$
, define
$\mathbf{j}=(j_{1},j_{2},\ldots ,j_{m+n})\in \mathbb{Z}^{m+n}$
, define
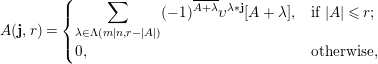 $$\begin{eqnarray}\displaystyle A(\mathbf{j},r)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r-|A|)}}(-1)^{\overline{A+\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D710}^{\unicode[STIX]{x1D706}\ast \mathbf{j}}[A+\unicode[STIX]{x1D706}],\quad & \text{if }|A|\leqslant r;\\ 0,\quad & \text{otherwise,}\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A(\mathbf{j},r)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r-|A|)}}(-1)^{\overline{A+\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D710}^{\unicode[STIX]{x1D706}\ast \mathbf{j}}[A+\unicode[STIX]{x1D706}],\quad & \text{if }|A|\leqslant r;\\ 0,\quad & \text{otherwise,}\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}\ast \mathbf{j}=\sum _{i=1}^{m+n}(-1)^{\widehat{i}}\unicode[STIX]{x1D706}_{i}j_{i}$
is the super (or signed) “dot product”,
$\unicode[STIX]{x1D706}\ast \mathbf{j}=\sum _{i=1}^{m+n}(-1)^{\widehat{i}}\unicode[STIX]{x1D706}_{i}j_{i}$
is the super (or signed) “dot product”,
![]() $A+\unicode[STIX]{x1D706}=A+\operatorname{diag}(\unicode[STIX]{x1D706})$
and
$A+\unicode[STIX]{x1D706}=A+\operatorname{diag}(\unicode[STIX]{x1D706})$
and
![]() $\overline{M}=\sum _{\substack{ m+n\geqslant i>m\geqslant k\geqslant 1 \\ m<j<l\leqslant m+n}}m_{i,j}m_{k,l}$
for a matrix
$\overline{M}=\sum _{\substack{ m+n\geqslant i>m\geqslant k\geqslant 1 \\ m<j<l\leqslant m+n}}m_{i,j}m_{k,l}$
for a matrix
![]() $M$
. We also let
$M$
. We also let
![]() $1_{\unicode[STIX]{x1D706}}=[\operatorname{diag}(\unicode[STIX]{x1D706})]$
for all
$1_{\unicode[STIX]{x1D706}}=[\operatorname{diag}(\unicode[STIX]{x1D706})]$
for all
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, the identity map on
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
, the identity map on
![]() $[xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R}$
. Then
$[xy]_{\unicode[STIX]{x1D706}}{\mathcal{H}}_{R}$
. Then
![]() $1_{\unicode[STIX]{x1D706}}[A]=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\text{ro}(A)}[A]$
. For the zero matrix
$1_{\unicode[STIX]{x1D706}}[A]=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\text{ro}(A)}[A]$
. For the zero matrix
![]() $O$
,
$O$
,
![]() $\mathbf{e}_{i}\in \unicode[STIX]{x1D6EC}(m|n,1)$
and
$\mathbf{e}_{i}\in \unicode[STIX]{x1D6EC}(m|n,1)$
and
![]() $p\geqslant 1$
, set
$p\geqslant 1$
, set
Note that
![]() ${\rm \small{k}}_{i}=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)}\unicode[STIX]{x1D710}^{(-1)^{\widehat{i}}\unicode[STIX]{x1D706}_{i}}1_{\unicode[STIX]{x1D706}}$
and
${\rm \small{k}}_{i}=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)}\unicode[STIX]{x1D710}^{(-1)^{\widehat{i}}\unicode[STIX]{x1D706}_{i}}1_{\unicode[STIX]{x1D706}}$
and
![]() ${\rm \small{e}}_{m}^{2}=0={\rm \small{f}}_{m}^{2}$
.
${\rm \small{e}}_{m}^{2}=0={\rm \small{f}}_{m}^{2}$
.
Let
![]() ${\mathcal{S}}_{R}^{-}$
,
${\mathcal{S}}_{R}^{-}$
,
![]() ${\mathcal{S}}_{R}^{+}$
be the subsuperalgebra of
${\mathcal{S}}_{R}^{+}$
be the subsuperalgebra of
![]() ${\mathcal{S}}_{R}(m|n,r)$
generated respectively by
${\mathcal{S}}_{R}(m|n,r)$
generated respectively by
![]() ${\rm \small{f}}_{h}^{(p)}$
,
${\rm \small{f}}_{h}^{(p)}$
,
![]() ${\rm \small{e}}_{h}^{(p)}$
for all
${\rm \small{e}}_{h}^{(p)}$
for all
![]() $1\leqslant h<m+n$
,
$1\leqslant h<m+n$
,
![]() $p\geqslant 1$
, and
$p\geqslant 1$
, and
![]() ${\mathcal{S}}_{R}^{0}$
the subsuperalgebra spanned by all
${\mathcal{S}}_{R}^{0}$
the subsuperalgebra spanned by all
![]() $1_{\unicode[STIX]{x1D706}}$
.
$1_{\unicode[STIX]{x1D706}}$
.
The first assertion of the following is [Reference Du and Gu12, Corollary 8.5].
Theorem 4.5. The
![]() $q$
-Schur superalgebra
$q$
-Schur superalgebra
![]() ${\mathcal{S}}_{R}={\mathcal{S}}_{R}(m|n,r)$
is generated by
${\mathcal{S}}_{R}={\mathcal{S}}_{R}(m|n,r)$
is generated by
![]() ${\rm \small{k}}_{i},$
${\rm \small{k}}_{i},$
![]() $1_{\unicode[STIX]{x1D706}},$
$1_{\unicode[STIX]{x1D706}},$
![]() ${\rm \small{e}}_{h}^{(p)},{\rm \small{f}}_{h}^{(p)}$
for all
${\rm \small{e}}_{h}^{(p)},{\rm \small{f}}_{h}^{(p)}$
for all
![]() $1\leqslant h,i\leqslant m+n,h\not =m+n,$
$1\leqslant h,i\leqslant m+n,h\not =m+n,$
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
,
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
,
![]() $1\leqslant p\leqslant r$
, and
$1\leqslant p\leqslant r$
, and
![]() ${\mathcal{S}}_{R}={\mathcal{S}}_{R}^{+}{\mathcal{S}}_{R}^{0}{\mathcal{S}}_{R}^{-}$
. These generators have the following matrix representations relative to the basis
${\mathcal{S}}_{R}={\mathcal{S}}_{R}^{+}{\mathcal{S}}_{R}^{0}{\mathcal{S}}_{R}^{-}$
. These generators have the following matrix representations relative to the basis
![]() $\{[A]\}_{A\in M(m|n,r)}$
:
$\{[A]\}_{A\in M(m|n,r)}$
:
- (0)
 ${\rm \small{k}}_{i}[A]=\unicode[STIX]{x1D710}^{(-1)^{\widehat{i}}\text{ro}(A)_{i}}[A]$
,
${\rm \small{k}}_{i}[A]=\unicode[STIX]{x1D710}^{(-1)^{\widehat{i}}\text{ro}(A)_{i}}[A]$
,
 $1_{\unicode[STIX]{x1D706}}[A]=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\text{ro}(A)}[A]$
;
$1_{\unicode[STIX]{x1D706}}[A]=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706},\text{ro}(A)}[A]$
;- (1)
 ${\rm \small{e}}_{h}^{(p)}[A]=\displaystyle \sum _{\substack{ \unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}(m|n,p) \\ \unicode[STIX]{x1D708}\leqslant \text{row}_{h+1}(A)}}\unicode[STIX]{x1D710}_{h}^{f_{h}^{+}(\unicode[STIX]{x1D708},A)}\prod _{k=1}^{m+n}\overline{\left[\left[{a_{h,k}+\unicode[STIX]{x1D708}_{k}\atop \unicode[STIX]{x1D708}_{k}}\right]\right]}_{\unicode[STIX]{x1D710}_{h}^{2}}[A+\sum _{l}\unicode[STIX]{x1D708}_{l}(E_{h,l}-E_{h+1,l})]$
,
${\rm \small{e}}_{h}^{(p)}[A]=\displaystyle \sum _{\substack{ \unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}(m|n,p) \\ \unicode[STIX]{x1D708}\leqslant \text{row}_{h+1}(A)}}\unicode[STIX]{x1D710}_{h}^{f_{h}^{+}(\unicode[STIX]{x1D708},A)}\prod _{k=1}^{m+n}\overline{\left[\left[{a_{h,k}+\unicode[STIX]{x1D708}_{k}\atop \unicode[STIX]{x1D708}_{k}}\right]\right]}_{\unicode[STIX]{x1D710}_{h}^{2}}[A+\sum _{l}\unicode[STIX]{x1D708}_{l}(E_{h,l}-E_{h+1,l})]$
,where
 $h\neq m$
,
$h\neq m$
,
 $f_{h}^{+}(\unicode[STIX]{x1D708},A)=\sum _{j\geqslant t}a_{h,j}\unicode[STIX]{x1D708}_{t}-\sum _{j>t}a_{h+1,j}\unicode[STIX]{x1D708}_{t}+\sum _{t<t^{\prime }}\unicode[STIX]{x1D708}_{t}\unicode[STIX]{x1D708}_{t^{\prime }}$
and
$f_{h}^{+}(\unicode[STIX]{x1D708},A)=\sum _{j\geqslant t}a_{h,j}\unicode[STIX]{x1D708}_{t}-\sum _{j>t}a_{h+1,j}\unicode[STIX]{x1D708}_{t}+\sum _{t<t^{\prime }}\unicode[STIX]{x1D708}_{t}\unicode[STIX]{x1D708}_{t^{\prime }}$
and
 $\unicode[STIX]{x1D708}\leqslant \unicode[STIX]{x1D708}^{\prime }$
means that
$\unicode[STIX]{x1D708}\leqslant \unicode[STIX]{x1D708}^{\prime }$
means that
 $\unicode[STIX]{x1D708}_{i}\leqslant \unicode[STIX]{x1D708}_{i}^{\prime }$
for all
$\unicode[STIX]{x1D708}_{i}\leqslant \unicode[STIX]{x1D708}_{i}^{\prime }$
for all
 $i$
;
$i$
;- (2)
 ${\rm \small{f}}_{h}^{(p)}[A]=\displaystyle \sum _{\substack{ \unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}(m|n,p) \\ \unicode[STIX]{x1D708}\leqslant \text{row}_{h}(A)}}\unicode[STIX]{x1D710}_{h+1}^{f_{h}^{-}(\unicode[STIX]{x1D708},A)}\prod _{k=1}^{m+n}\overline{\left[\left[{a_{h+1,k}+\unicode[STIX]{x1D708}_{k}\atop \unicode[STIX]{x1D708}_{k}}\right]\right]}_{\unicode[STIX]{x1D710}_{h+1}^{2}}[A-\sum _{l}\unicode[STIX]{x1D708}_{l}(E_{h,l}-E_{h+1,l})]$
,
${\rm \small{f}}_{h}^{(p)}[A]=\displaystyle \sum _{\substack{ \unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6EC}(m|n,p) \\ \unicode[STIX]{x1D708}\leqslant \text{row}_{h}(A)}}\unicode[STIX]{x1D710}_{h+1}^{f_{h}^{-}(\unicode[STIX]{x1D708},A)}\prod _{k=1}^{m+n}\overline{\left[\left[{a_{h+1,k}+\unicode[STIX]{x1D708}_{k}\atop \unicode[STIX]{x1D708}_{k}}\right]\right]}_{\unicode[STIX]{x1D710}_{h+1}^{2}}[A-\sum _{l}\unicode[STIX]{x1D708}_{l}(E_{h,l}-E_{h+1,l})]$
,where
 $h\neq m$
and
$h\neq m$
and
 $f_{h}^{-}(\unicode[STIX]{x1D708},A)=\sum _{j\leqslant t}a_{h+1,j}\unicode[STIX]{x1D708}_{t}-\sum _{j<t}a_{h,j}\unicode[STIX]{x1D708}_{t}+\sum _{t<t^{\prime }}\unicode[STIX]{x1D708}_{t}\unicode[STIX]{x1D708}_{t^{\prime }}$
;
$f_{h}^{-}(\unicode[STIX]{x1D708},A)=\sum _{j\leqslant t}a_{h+1,j}\unicode[STIX]{x1D708}_{t}-\sum _{j<t}a_{h,j}\unicode[STIX]{x1D708}_{t}+\sum _{t<t^{\prime }}\unicode[STIX]{x1D708}_{t}\unicode[STIX]{x1D708}_{t^{\prime }}$
;- (3)
 ${\rm \small{e}}_{m}[A]=\displaystyle \sum _{{k\atop a_{m+1,k}\geqslant 1}}(-1)^{\sum _{i>m,j<k}a_{i,j}}\unicode[STIX]{x1D710}_{m}^{f_{m,k}^{+}(A)}\overline{\unicode[STIX]{x27E6}a_{m,k}+1\unicode[STIX]{x27E7}}_{\unicode[STIX]{x1D710}_{m}^{2}}[A_{m,k}^{+}]$
,
${\rm \small{e}}_{m}[A]=\displaystyle \sum _{{k\atop a_{m+1,k}\geqslant 1}}(-1)^{\sum _{i>m,j<k}a_{i,j}}\unicode[STIX]{x1D710}_{m}^{f_{m,k}^{+}(A)}\overline{\unicode[STIX]{x27E6}a_{m,k}+1\unicode[STIX]{x27E7}}_{\unicode[STIX]{x1D710}_{m}^{2}}[A_{m,k}^{+}]$
,where
 $f_{m,k}^{+}(A)=\sum _{j\geqslant k}a_{m,j}+\sum _{j>k}a_{m+1,j}$
;
$f_{m,k}^{+}(A)=\sum _{j\geqslant k}a_{m,j}+\sum _{j>k}a_{m+1,j}$
;- (4)
 ${\rm \small{f}}_{m}[A]=\displaystyle \sum _{{k\atop a_{m,k}\geqslant 1}}(-1)^{\sum _{i>m,j<k}a_{i,j}}\unicode[STIX]{x1D710}_{m+1}^{f_{m,k}^{-}(A)}\overline{\unicode[STIX]{x27E6}a_{m+1,k}+1\unicode[STIX]{x27E7}}_{\unicode[STIX]{x1D710}_{m+1}^{2}}[A_{m,k}^{-}]$
,
${\rm \small{f}}_{m}[A]=\displaystyle \sum _{{k\atop a_{m,k}\geqslant 1}}(-1)^{\sum _{i>m,j<k}a_{i,j}}\unicode[STIX]{x1D710}_{m+1}^{f_{m,k}^{-}(A)}\overline{\unicode[STIX]{x27E6}a_{m+1,k}+1\unicode[STIX]{x27E7}}_{\unicode[STIX]{x1D710}_{m+1}^{2}}[A_{m,k}^{-}]$
,where
 $f_{m,k}^{-}(A)=\sum _{j\leqslant k}a_{m+1,j}+\sum _{j<k}a_{m,j}$
.
$f_{m,k}^{-}(A)=\sum _{j\leqslant k}a_{m+1,j}+\sum _{j<k}a_{m,j}$
.
Proof. The first assertion follows from [Reference Du and Gu12, Corollary 8.5] (cf. [Reference Du and Gu12, Theorem 6.3]). Now the relations in (0) are clear. Since
![]() ${\rm \small{e}}_{h}^{(p)}[A]={\rm \small{e}}_{h}^{(p)}1_{\text{ro}(A)}[A]$
,
${\rm \small{e}}_{h}^{(p)}[A]={\rm \small{e}}_{h}^{(p)}1_{\text{ro}(A)}[A]$
,
![]() ${\rm \small{f}}_{h}^{(p)}[A]={\rm \small{f}}_{h}^{(p)}1_{\text{ro}(A)}[A]$
, and
${\rm \small{f}}_{h}^{(p)}[A]={\rm \small{f}}_{h}^{(p)}1_{\text{ro}(A)}[A]$
, and
![]() ${\rm \small{e}}_{h}^{(p)}1_{\text{ro}(A)}=(-1)^{\overline{D_{h,p}^{+}}}[D_{h,p}^{+}]$
,
${\rm \small{e}}_{h}^{(p)}1_{\text{ro}(A)}=(-1)^{\overline{D_{h,p}^{+}}}[D_{h,p}^{+}]$
,
![]() ${\rm \small{f}}_{h}^{(p)}1_{\text{ro}(A)}=(-1)^{\overline{D_{h,p}^{-}}}[D_{h,p}^{-}]$
, where the matrices
${\rm \small{f}}_{h}^{(p)}1_{\text{ro}(A)}=(-1)^{\overline{D_{h,p}^{-}}}[D_{h,p}^{-}]$
, where the matrices
![]() $D_{h,p}^{\pm }\in M(m|n,r)$
are defined by the conditions that
$D_{h,p}^{\pm }\in M(m|n,r)$
are defined by the conditions that
![]() $\text{co}(D_{h,p}^{\pm })=\text{ro}(A)$
and
$\text{co}(D_{h,p}^{\pm })=\text{ro}(A)$
and
![]() $D_{h,p}^{+}-pE_{h,h+1}$
,
$D_{h,p}^{+}-pE_{h,h+1}$
,
![]() $D_{h,p}^{-}-pE_{h+1,h}$
are diagonal, (1) and (2) follow from [Reference Du and Gu12, Proposition 4.4]Footnote
2
and [Reference Du and Gu12, Lemma 5.1(1)] which tells
$D_{h,p}^{-}-pE_{h+1,h}$
are diagonal, (1) and (2) follow from [Reference Du and Gu12, Proposition 4.4]Footnote
2
and [Reference Du and Gu12, Lemma 5.1(1)] which tells
![]() $\overline{D_{h,p}^{\pm }}=0$
. The remaining (3) and (4) follow from the
$\overline{D_{h,p}^{\pm }}=0$
. The remaining (3) and (4) follow from the
![]() $h=m$
case of Corollary 4.4; see [Reference Du and Gu12, Proposition 4.5].
$h=m$
case of Corollary 4.4; see [Reference Du and Gu12, Proposition 4.5].
Note that we have in
![]() ${\mathcal{S}}_{F}(m|n,r)$
${\mathcal{S}}_{F}(m|n,r)$
5 Semisimple
 $q$
-Schur superalgebras
$q$
-Schur superalgebras
The most fabulous application of the multiplication formulas is the realizations of quantum
![]() $\mathfrak{g}\mathfrak{l}_{n}$
[Reference Beilinson, Lusztig and MacPherson1] and quantum super
$\mathfrak{g}\mathfrak{l}_{n}$
[Reference Beilinson, Lusztig and MacPherson1] and quantum super
![]() $\mathfrak{g}\mathfrak{l}_{m|n}$
[Reference Du and Gu12]. We now use these formulas to construct certain modules from which we obtain a semisimplicity criterion of
$\mathfrak{g}\mathfrak{l}_{m|n}$
[Reference Du and Gu12]. We now use these formulas to construct certain modules from which we obtain a semisimplicity criterion of
![]() $q$
-Schur superalgebras. From now on, let
$q$
-Schur superalgebras. From now on, let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $\neq 2$
and assume that
$\neq 2$
and assume that
![]() $\unicode[STIX]{x1D710}\in F^{\times }$
and
$\unicode[STIX]{x1D710}\in F^{\times }$
and
![]() $q=\unicode[STIX]{x1D710}^{2}\neq 1$
. Since every simple
$q=\unicode[STIX]{x1D710}^{2}\neq 1$
. Since every simple
![]() ${\mathcal{S}}_{F}(m|n,r)$
-supermodule is also a simple
${\mathcal{S}}_{F}(m|n,r)$
-supermodule is also a simple
![]() ${\mathcal{S}}_{F}(m|n,r)$
-module (see e.g., [Reference Du, Gu and Wang15, Proposition 4.1]), we will drop the prefix “super” in the sequel for simplicity.
${\mathcal{S}}_{F}(m|n,r)$
-module (see e.g., [Reference Du, Gu and Wang15, Proposition 4.1]), we will drop the prefix “super” in the sequel for simplicity.
We first determine the semisimplicity for
![]() ${\mathcal{S}}_{F}(1|1,r)$
(see [Reference Marko and Zubkov25] for the
${\mathcal{S}}_{F}(1|1,r)$
(see [Reference Marko and Zubkov25] for the
![]() $q=1$
case).
$q=1$
case).
Lemma 5.1. Assume that
![]() $q\neq 1$
is a primitive
$q\neq 1$
is a primitive
![]() $l$
-th root of unity.
$l$
-th root of unity.
(1) If
 $l\nmid r$
then
$l\nmid r$
then
 ${\mathcal{S}}_{F}(1|1,r)$
is semisimple and has exact
${\mathcal{S}}_{F}(1|1,r)$
is semisimple and has exact
 $r$
nonisomorphic irreducible modules which are all two dimensional.
$r$
nonisomorphic irreducible modules which are all two dimensional.(2) If
 $l\mid r$
then
$l\mid r$
then
 ${\mathcal{S}}_{F}(1|1,r)$
is not semisimple and has exact
${\mathcal{S}}_{F}(1|1,r)$
is not semisimple and has exact
 $r+1$
nonisomorphic irreducible modules which are all one dimensional.
$r+1$
nonisomorphic irreducible modules which are all one dimensional.
Proof. Let
![]() ${\mathcal{S}}_{F}={\mathcal{S}}_{F}(1|1,r)$
. We first observe that
${\mathcal{S}}_{F}={\mathcal{S}}_{F}(1|1,r)$
. We first observe that
where
![]() $A_{a},A_{b}^{+},A_{c}^{-},A_{d}^{\pm }$
denote respectively the following matrices
$A_{a},A_{b}^{+},A_{c}^{-},A_{d}^{\pm }$
denote respectively the following matrices
Note that
![]() $1_{a}:=1_{(a,r-a)}=[A_{a}]$
and
$1_{a}:=1_{(a,r-a)}=[A_{a}]$
and
![]() $\sum _{a=0}^{r}1_{a}$
is the identity element. So
$\sum _{a=0}^{r}1_{a}$
is the identity element. So
Since
![]() ${\mathcal{S}}_{F}1_{a}$
is spanned by
${\mathcal{S}}_{F}1_{a}$
is spanned by
![]() $[A]$
with
$[A]$
with
![]() $\text{co}(A)=(a,r-a)$
, it follows that
$\text{co}(A)=(a,r-a)$
, it follows that
By Theorem 4.5(3) and (4), we have
If
![]() $l\nmid r$
, then
$l\nmid r$
, then
![]() $\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}_{q}=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}_{q^{-1}}\neq 0$
in
$\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}_{q}=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}r\unicode[STIX]{x27E7}_{q^{-1}}\neq 0$
in
![]() $F$
, and we see easily that
$F$
, and we see easily that
![]() $L(1):={\mathcal{S}}_{F}1_{0}$
is irreducible. Similarly,
$L(1):={\mathcal{S}}_{F}1_{0}$
is irreducible. Similarly,
![]() $L(r):={\mathcal{S}}_{F}1_{r}$
is irreducible if
$L(r):={\mathcal{S}}_{F}1_{r}$
is irreducible if
![]() $l\nmid r$
.
$l\nmid r$
.
If
![]() $l\mid r$
, then
$l\mid r$
, then
![]() $L(1)$
is indecomposable and
$L(1)$
is indecomposable and
![]() $[A_{0}^{+}]$
spans a submodule
$[A_{0}^{+}]$
spans a submodule
![]() $\overline{L}(1)$
of
$\overline{L}(1)$
of
![]() $L(1)$
. Let
$L(1)$
. Let
![]() $\overline{L}(0)=L(1)/\overline{L}(1)$
. Similarly,
$\overline{L}(0)=L(1)/\overline{L}(1)$
. Similarly,
![]() $[A_{r-1}^{-}]$
spans a submodule
$[A_{r-1}^{-}]$
spans a submodule
![]() $\overline{L}(r-1)$
. Let
$\overline{L}(r-1)$
. Let
![]() $\overline{L}(r)=L(r)/\overline{L}(r-1)$
.
$\overline{L}(r)=L(r)/\overline{L}(r-1)$
.
For
![]() $a\in [1,r-1]$
, applying Theorem 4.5 again yields
$a\in [1,r-1]$
, applying Theorem 4.5 again yields
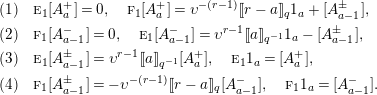 $$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\displaystyle (1)\quad {\rm \small{e}}_{1}[A_{a}^{+}]=0,\quad {\rm \small{f}}_{1}[A_{a}^{+}]=\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}1_{a}+[A_{a-1}^{\pm }],\\ \displaystyle (2)\quad {\rm \small{f}}_{1}[A_{a-1}^{-}]=0,\quad {\rm \small{e}}_{1}[A_{a-1}^{-}]=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}1_{a}-[A_{a-1}^{\pm }],\\ \displaystyle (3)\quad {\rm \small{e}}_{1}[A_{a-1}^{\pm }]=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}[A_{a}^{+}],\quad {\rm \small{e}}_{1}1_{a}=[A_{a}^{+}],\\ \displaystyle (4)\quad {\rm \small{f}}_{1}[A_{a-1}^{\pm }]=-\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}[A_{a-1}^{-}],\quad {\rm \small{f}}_{1}1_{a}=[A_{a-1}^{-}].\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\displaystyle (1)\quad {\rm \small{e}}_{1}[A_{a}^{+}]=0,\quad {\rm \small{f}}_{1}[A_{a}^{+}]=\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}1_{a}+[A_{a-1}^{\pm }],\\ \displaystyle (2)\quad {\rm \small{f}}_{1}[A_{a-1}^{-}]=0,\quad {\rm \small{e}}_{1}[A_{a-1}^{-}]=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}1_{a}-[A_{a-1}^{\pm }],\\ \displaystyle (3)\quad {\rm \small{e}}_{1}[A_{a-1}^{\pm }]=\unicode[STIX]{x1D710}^{r-1}\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}[A_{a}^{+}],\quad {\rm \small{e}}_{1}1_{a}=[A_{a}^{+}],\\ \displaystyle (4)\quad {\rm \small{f}}_{1}[A_{a-1}^{\pm }]=-\unicode[STIX]{x1D710}^{-(r-1)}\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}[A_{a-1}^{-}],\quad {\rm \small{f}}_{1}1_{a}=[A_{a-1}^{-}].\end{array} & & \displaystyle\end{eqnarray}$$
Let
If
![]() $l\nmid r$
, we claim that
$l\nmid r$
, we claim that
![]() ${\mathcal{S}}_{F}1_{a}=L(a+1)\oplus L(a)$
is a direct sum of irreducible submodules. Indeed,
${\mathcal{S}}_{F}1_{a}=L(a+1)\oplus L(a)$
is a direct sum of irreducible submodules. Indeed,
![]() $\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}$
and
$\unicode[STIX]{x27E6}a\unicode[STIX]{x27E7}_{q^{-1}}$
and
![]() $\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}$
cannot be both zero in this case. So
$\unicode[STIX]{x27E6}r-a\unicode[STIX]{x27E7}_{q}$
cannot be both zero in this case. So
![]() $L(a+1)\cap L(a)=0$
, forcing
$L(a+1)\cap L(a)=0$
, forcing
![]() ${\mathcal{S}}_{F}1_{a}=L(a+1)\oplus L(a)$
as vector spaces. Since, by (4.5.1),
${\mathcal{S}}_{F}1_{a}=L(a+1)\oplus L(a)$
as vector spaces. Since, by (4.5.1),
and
![]() $(\unicode[STIX]{x1D710}^{r}-\unicode[STIX]{x1D710}^{-r})/(\unicode[STIX]{x1D710}-\unicode[STIX]{x1D710}^{-1})\neq 0$
, every nonzero element in
$(\unicode[STIX]{x1D710}^{r}-\unicode[STIX]{x1D710}^{-r})/(\unicode[STIX]{x1D710}-\unicode[STIX]{x1D710}^{-1})\neq 0$
, every nonzero element in
![]() $L(a+1)$
generates
$L(a+1)$
generates
![]() $L(a+1)$
. Hence,
$L(a+1)$
. Hence,
![]() $L(a+1)$
is an irreducible submodule. Likewise,
$L(a+1)$
is an irreducible submodule. Likewise,
![]() $L(a)$
is a submodule. This proves that
$L(a)$
is a submodule. This proves that
![]() ${\mathcal{S}}_{F}1_{a}$
is semisimple for all
${\mathcal{S}}_{F}1_{a}$
is semisimple for all
![]() $a\in [1,r-1]$
. Hence,
$a\in [1,r-1]$
. Hence,
![]() ${\mathcal{S}}_{F}$
is semisimple.
${\mathcal{S}}_{F}$
is semisimple.
Assume now
![]() $l\mid r$
. Then, by (5.1.2),
$l\mid r$
. Then, by (5.1.2),
![]() ${\rm \small{e}}_{1}({\rm \small{f}}_{1}[A_{a}^{+}])=0$
. On the other hand,
${\rm \small{e}}_{1}({\rm \small{f}}_{1}[A_{a}^{+}])=0$
. On the other hand,
![]() ${\rm \small{f}}_{1}^{2}=0$
implies
${\rm \small{f}}_{1}^{2}=0$
implies
![]() ${\rm \small{f}}_{1}({\rm \small{f}}_{1}[A_{a}^{+}])=0$
. Thus,
${\rm \small{f}}_{1}({\rm \small{f}}_{1}[A_{a}^{+}])=0$
. Thus,
![]() ${\rm \small{f}}_{1}[A_{a}^{+}]$
spans a submodule
${\rm \small{f}}_{1}[A_{a}^{+}]$
spans a submodule
![]() $\overline{L}(a)$
of
$\overline{L}(a)$
of
![]() $L(a+1)$
. Similarly,
$L(a+1)$
. Similarly,
![]() ${\rm \small{e}}_{1}[A_{a-1}^{-}]$
spans a submodule
${\rm \small{e}}_{1}[A_{a-1}^{-}]$
spans a submodule
![]() $\overline{L}(a)^{\prime }(\cong \overline{L}(a))$
of
$\overline{L}(a)^{\prime }(\cong \overline{L}(a))$
of
![]() $L(a)$
. Moreover, (cf. [Reference Marko and Zubkov25, Theorem 1])
$L(a)$
. Moreover, (cf. [Reference Marko and Zubkov25, Theorem 1])
Hence,
![]() $\overline{L}(a),0\leqslant a\leqslant r,$
form a complete set of all irreducible
$\overline{L}(a),0\leqslant a\leqslant r,$
form a complete set of all irreducible
![]() ${\mathcal{S}}_{F}$
-modules.
${\mathcal{S}}_{F}$
-modules.
Remark 5.2. The classification of irreducible modules for
![]() ${\mathcal{S}}_{k}(1|1,r)$
in the semisimple case is consistent with a classification given in [Reference Du and Rui16, Theorem 7.5].
${\mathcal{S}}_{k}(1|1,r)$
in the semisimple case is consistent with a classification given in [Reference Du and Rui16, Theorem 7.5].
Lemma 5.3. With the same assumption on
![]() $l$
as in Lemma 5.1, the superalgebras
$l$
as in Lemma 5.1, the superalgebras
![]() ${\mathcal{S}}_{F}(2|1,r)$
and
${\mathcal{S}}_{F}(2|1,r)$
and
![]() ${\mathcal{S}}_{F}(1|2,r)$
are not semisimple for all
${\mathcal{S}}_{F}(1|2,r)$
are not semisimple for all
![]() $r\geqslant l$
.
$r\geqslant l$
.
Proof. By Lemma 2.1, it suffices to consider
![]() ${\mathcal{S}}_{F}={\mathcal{S}}_{F}(2|1,r)$
. Let
${\mathcal{S}}_{F}={\mathcal{S}}_{F}(2|1,r)$
. Let
![]() $e=1_{(r,0,0)}$
. Then, for
$e=1_{(r,0,0)}$
. Then, for
![]() $P={\mathcal{S}}_{F}e$
,
$P={\mathcal{S}}_{F}e$
,
![]() $\text{End}_{{\mathcal{S}}_{F}}(P)\cong F$
and so
$\text{End}_{{\mathcal{S}}_{F}}(P)\cong F$
and so
![]() $P$
is an indecomposable
$P$
is an indecomposable
![]() ${\mathcal{S}}_{F}$
-module. We now show the existence of a proper submodule of
${\mathcal{S}}_{F}$
-module. We now show the existence of a proper submodule of
![]() $P$
if
$P$
if
![]() $r\geqslant l$
. Observe that
$r\geqslant l$
. Observe that
![]() $P$
is spanned by all
$P$
is spanned by all
![]() $[A]$
with
$[A]$
with
![]() $\text{co}(A)=(r,0,0)$
. Such
$\text{co}(A)=(r,0,0)$
. Such
![]() $A$
will be written as
$A$
will be written as
![]() $A_{a,b,c}$
where
$A_{a,b,c}$
where
![]() $(a,b,c)^{t}$
is the first column of
$(a,b,c)^{t}$
is the first column of
![]() $A$
. We have two cases to consider.
$A$
. We have two cases to consider.
Case 1. If
![]() $r=al+b$
with
$r=al+b$
with
![]() $0\leqslant b\leqslant l-2$
(i.e.,
$0\leqslant b\leqslant l-2$
(i.e.,
![]() $l\nmid r+1$
), then
$l\nmid r+1$
), then
![]() $b+1<l$
and
$b+1<l$
and
![]() ${\rm \small{f}}_{1}^{(b+1)}e=[A_{al-1,b+1,0}]\in P$
. We now claim that
${\rm \small{f}}_{1}^{(b+1)}e=[A_{al-1,b+1,0}]\in P$
. We now claim that
![]() $[A_{al-1,b+1,0}]$
is a maximal vector in the sense that
$[A_{al-1,b+1,0}]$
is a maximal vector in the sense that
![]() ${\rm \small{e}}_{h}^{(p)}[A_{al-1,b+1,0}]=0$
for all
${\rm \small{e}}_{h}^{(p)}[A_{al-1,b+1,0}]=0$
for all
![]() $h=1,2$
and
$h=1,2$
and
![]() $p\geqslant 1$
. This is clear if
$p\geqslant 1$
. This is clear if
![]() $h=2$
since all
$h=2$
since all
![]() $a_{h+1,k}=a_{3,k}=0$
. Also, by Theorem 4.5(1), we have
$a_{h+1,k}=a_{3,k}=0$
. Also, by Theorem 4.5(1), we have
![]() ${\rm \small{e}}_{1}^{(p)}[A_{al-1,b+1,0}]=0$
for
${\rm \small{e}}_{1}^{(p)}[A_{al-1,b+1,0}]=0$
for
![]() $p>b+1$
and, for
$p>b+1$
and, for
![]() $p\leqslant b+1<l$
,
$p\leqslant b+1<l$
,
By the claim, we see that
![]() $P^{\prime }:={\mathcal{S}}_{F}[A_{al-1,b+1,0}]={\mathcal{S}}_{F}^{-}[A_{al-1,b+1,0}]$
is a proper submodule of
$P^{\prime }:={\mathcal{S}}_{F}[A_{al-1,b+1,0}]={\mathcal{S}}_{F}^{-}[A_{al-1,b+1,0}]$
is a proper submodule of
![]() $P$
since
$P$
since
![]() $e\not \in P^{\prime }$
.
$e\not \in P^{\prime }$
.
Case 2. If
![]() $r=al-1$
(and so
$r=al-1$
(and so
![]() $a\geqslant 2$
), then by Theorem 4.5,
$a\geqslant 2$
), then by Theorem 4.5,
![]() ${\rm \small{f}}_{2}({\rm \small{f}}_{1}^{(l)}e)={\rm \small{f}}_{2}[A_{r-l,l,0}]=[A_{r-l,l-1,1}]\in P.$
Now, since
${\rm \small{f}}_{2}({\rm \small{f}}_{1}^{(l)}e)={\rm \small{f}}_{2}[A_{r-l,l,0}]=[A_{r-l,l-1,1}]\in P.$
Now, since
![]() $r-l+1=(a-1)l$
, we have
$r-l+1=(a-1)l$
, we have
![]() ${\rm \small{e}}_{1}[A_{r-l,l-1,1}]=\unicode[STIX]{x1D710}^{r-l}\unicode[STIX]{x27E6}r-l+1\unicode[STIX]{x27E7}_{q^{-1}}[A_{r-l+1,l-2,1}]=0$
and
${\rm \small{e}}_{1}[A_{r-l,l-1,1}]=\unicode[STIX]{x1D710}^{r-l}\unicode[STIX]{x27E6}r-l+1\unicode[STIX]{x27E7}_{q^{-1}}[A_{r-l+1,l-2,1}]=0$
and
![]() ${\rm \small{e}}_{2}[A_{r-l,l-1,1}]=\unicode[STIX]{x1D710}^{l-1}\unicode[STIX]{x27E6}l\unicode[STIX]{x27E7}_{q^{-1}}[A_{r-l,l,0}]=0$
. Hence,
${\rm \small{e}}_{2}[A_{r-l,l-1,1}]=\unicode[STIX]{x1D710}^{l-1}\unicode[STIX]{x27E6}l\unicode[STIX]{x27E7}_{q^{-1}}[A_{r-l,l,0}]=0$
. Hence,
![]() ${\rm \small{e}}_{h}^{(p)}[A_{r-l,l-1,1}]=0$
for all
${\rm \small{e}}_{h}^{(p)}[A_{r-l,l-1,1}]=0$
for all
![]() $h=1,2$
and
$h=1,2$
and
![]() $p<l$
. Similarly, by Theorem 4.5(1),
$p<l$
. Similarly, by Theorem 4.5(1),
![]() ${\rm \small{e}}_{h}^{(p)}[A_{r-l,l-1,1}]=0$
for
${\rm \small{e}}_{h}^{(p)}[A_{r-l,l-1,1}]=0$
for
![]() $h=1,2$
and
$h=1,2$
and
![]() $p\geqslant l$
. This proves that
$p\geqslant l$
. This proves that
![]() ${\mathcal{S}}_{F}[A_{r-l,l-1,1}]={\mathcal{S}}_{F}^{-}[A_{r-l,l-1,1}]$
is a proper submodule of
${\mathcal{S}}_{F}[A_{r-l,l-1,1}]={\mathcal{S}}_{F}^{-}[A_{r-l,l-1,1}]$
is a proper submodule of
![]() $P$
.
$P$
.
Combining the two cases, we conclude that
![]() ${\mathcal{S}}_{F}$
is not semisimple whenever
${\mathcal{S}}_{F}$
is not semisimple whenever
![]() $r\geqslant l$
.
$r\geqslant l$
.
The following result is the quantum analogue of a result of Marko and Zubkov [Reference Marko and Zubkov26], which is stated in the abstract.
Theorem 5.4. Let
![]() $F$
be a field containing elements
$F$
be a field containing elements
![]() $q\neq 0,1$
. Then the
$q\neq 0,1$
. Then the
![]() $q$
-Schur superalgebra
$q$
-Schur superalgebra
![]() ${\mathcal{S}}_{F}(m|n,r)$
with
${\mathcal{S}}_{F}(m|n,r)$
with
![]() $m,n\geqslant 1$
is semisimple if and only if one of the following holds:
$m,n\geqslant 1$
is semisimple if and only if one of the following holds:
(1)
 $q$
is not a root of unity;
$q$
is not a root of unity;(2)
 $q$
is a primitive
$q$
is a primitive
 $l$
th root of unity and
$l$
th root of unity and
 $r<l$
;
$r<l$
;(3)
 $m=n=1$
and
$m=n=1$
and
 $q$
is an
$q$
is an
 $l$
th root of unity with
$l$
th root of unity with
 $l\nmid r$
.
$l\nmid r$
.
Proof. The first two conditions imply that
![]() ${\mathcal{H}}_{F}$
is semisimple and so is
${\mathcal{H}}_{F}$
is semisimple and so is
![]() ${\mathcal{S}}_{F}$
. The semisimplicity under (3) follows from Lemma 5.1. We now show that, if all three conditions fail, then
${\mathcal{S}}_{F}$
. The semisimplicity under (3) follows from Lemma 5.1. We now show that, if all three conditions fail, then
![]() ${\mathcal{S}}_{F}$
is not semisimple. By Lemmas 2.1 and 5.1, it suffices to look at the case for
${\mathcal{S}}_{F}$
is not semisimple. By Lemmas 2.1 and 5.1, it suffices to look at the case for
![]() $m\geqslant 2$
and
$m\geqslant 2$
and
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $l\leqslant r$
.
$l\leqslant r$
.
Consider the subset
and let
![]() $f=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)^{\prime }}1_{\unicode[STIX]{x1D706}}$
and
$f=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)^{\prime }}1_{\unicode[STIX]{x1D706}}$
and
![]() $e=1_{(r,0,\ldots ,0)}$
. Then
$e=1_{(r,0,\ldots ,0)}$
. Then
![]() $ef=e=fe$
and it is clear that there is an algebra isomorphism
$ef=e=fe$
and it is clear that there is an algebra isomorphism
![]() ${\mathcal{S}}_{F}(2|1,r)\cong f{\mathcal{S}}_{F}(m|n,r)f$
. By identifying the two algebras under this isomorphism, we see that there is an
${\mathcal{S}}_{F}(2|1,r)\cong f{\mathcal{S}}_{F}(m|n,r)f$
. By identifying the two algebras under this isomorphism, we see that there is an
![]() $f{\mathcal{S}}_{F}(m|n,r)f$
-module isomorphism
$f{\mathcal{S}}_{F}(m|n,r)f$
-module isomorphism
![]() ${\mathcal{S}}_{F}(2|1,r)1_{(r,0,0)}\cong f{\mathcal{S}}_{F}(m|n,r)e$
. This
${\mathcal{S}}_{F}(2|1,r)1_{(r,0,0)}\cong f{\mathcal{S}}_{F}(m|n,r)e$
. This
![]() $f{\mathcal{S}}_{F}(m|n,r)f$
-module is indecomposable, but not irreducible, by Lemma 5.3. Since
$f{\mathcal{S}}_{F}(m|n,r)f$
-module is indecomposable, but not irreducible, by Lemma 5.3. Since
![]() ${\mathcal{S}}_{F}(m|n,r)e$
is indecomposable and its image
${\mathcal{S}}_{F}(m|n,r)e$
is indecomposable and its image
![]() $f{\mathcal{S}}_{F}(m|n,r)e$
under the “Schur functor” is indecomposable, but not irreducible, we conclude that
$f{\mathcal{S}}_{F}(m|n,r)e$
under the “Schur functor” is indecomposable, but not irreducible, we conclude that
![]() ${\mathcal{S}}_{F}(m|n,r)e$
is not irreducible (see [Reference Green22, (6.2g)]). Hence,
${\mathcal{S}}_{F}(m|n,r)e$
is not irreducible (see [Reference Green22, (6.2g)]). Hence,
![]() ${\mathcal{S}}_{F}(m|n,r)$
is not semisimple.
${\mathcal{S}}_{F}(m|n,r)$
is not semisimple.
Remark 5.5. Semisimple
![]() $q$
-Schur algebras have been classified by K. Erdmann and D. Nakano [Reference Erdmann and Nakano18, Section 1.3, Theorem (A)]. By Corollary 4.2, we may also use this new approach to get their result; see appendix A.
$q$
-Schur algebras have been classified by K. Erdmann and D. Nakano [Reference Erdmann and Nakano18, Section 1.3, Theorem (A)]. By Corollary 4.2, we may also use this new approach to get their result; see appendix A.
6 Infinitesimal and little
 $q$
-Schur superalgebras
$q$
-Schur superalgebras
We now give another application of the multiplication formulas. We first construct certain subsuperalgebras of the
![]() $q$
-Schur superalgebra
$q$
-Schur superalgebra
![]() ${\mathcal{S}}_{R}(m|n,r)$
over the commutative ring
${\mathcal{S}}_{R}(m|n,r)$
over the commutative ring
![]() $R$
in which
$R$
in which
![]() $q=\unicode[STIX]{x1D710}^{2}\neq 1$
is a primitive
$q=\unicode[STIX]{x1D710}^{2}\neq 1$
is a primitive
![]() $l$
-th root of unity. (So
$l$
-th root of unity. (So
![]() $l\geqslant 2$
.)
$l\geqslant 2$
.)
Let
![]() $\mathfrak{s}_{R}(m|n,r)$
be the
$\mathfrak{s}_{R}(m|n,r)$
be the
![]() $R$
-submodule spanned by all
$R$
-submodule spanned by all
![]() $[A]$
with
$[A]$
with
![]() $A\in M(m|n,r)_{l}$
, where
$A\in M(m|n,r)_{l}$
, where
We have the following super analogue of the infinitesimal
![]() $q$
-Schur algebras (cf. [Reference Chen, Gu and Wang3]).
$q$
-Schur algebras (cf. [Reference Chen, Gu and Wang3]).
Theorem 6.1. The
![]() $R$
-submodule
$R$
-submodule
![]() $\mathfrak{s}_{R}(m|n,r)$
is a subsuperalgebra generated by
$\mathfrak{s}_{R}(m|n,r)$
is a subsuperalgebra generated by
![]() ${\rm \small{e}}_{h},{\rm \small{f}}_{h},1_{\unicode[STIX]{x1D706}}$
for all
${\rm \small{e}}_{h},{\rm \small{f}}_{h},1_{\unicode[STIX]{x1D706}}$
for all
![]() $1\leqslant h<m+n$
,
$1\leqslant h<m+n$
,
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
.
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
.
Proof. Let
![]() $\mathfrak{s}_{R}^{\prime }(m|n,r)$
be the subalgebra generated by
$\mathfrak{s}_{R}^{\prime }(m|n,r)$
be the subalgebra generated by
![]() $[aE_{h,h+1}+D]$
and
$[aE_{h,h+1}+D]$
and
![]() $[bE_{h+1,h}+D^{\prime }]$
, where
$[bE_{h+1,h}+D^{\prime }]$
, where
![]() $D,D^{\prime }$
are diagonal matrices with
$D,D^{\prime }$
are diagonal matrices with
![]() $aE_{h,h+1}+D,bE_{h+1,h}+D^{\prime }\in M(m|n,r)_{l}$
and
$aE_{h,h+1}+D,bE_{h+1,h}+D^{\prime }\in M(m|n,r)_{l}$
and
![]() $0\leqslant a,b<l$
. Observe from the multiplication formulas in Theorem 4.5 that if
$0\leqslant a,b<l$
. Observe from the multiplication formulas in Theorem 4.5 that if
![]() $A\in M(m|n,r)_{l}$
then
$A\in M(m|n,r)_{l}$
then
![]() ${\rm \small{e}}_{h}^{(a)}[A]=[aE_{h,h+1}+D][A]$
and
${\rm \small{e}}_{h}^{(a)}[A]=[aE_{h,h+1}+D][A]$
and
![]() ${\rm \small{f}}_{h}^{(b)}[A]=[bE_{h+1,h}+D^{\prime }][A]$
, for some
${\rm \small{f}}_{h}^{(b)}[A]=[bE_{h+1,h}+D^{\prime }][A]$
, for some
![]() $D,D^{\prime }$
, are linear combinations of
$D,D^{\prime }$
, are linear combinations of
![]() $[B]$
with
$[B]$
with
![]() $B\in M(m|n,r)_{l}$
. This implies that
$B\in M(m|n,r)_{l}$
. This implies that
![]() $\mathfrak{s}_{R}^{\prime }(m|n,r)\subseteq \mathfrak{s}_{R}(m|n,r)$
. Now, by the triangular relation [Reference Du and Gu12, Theorem 7.4]:
$\mathfrak{s}_{R}^{\prime }(m|n,r)\subseteq \mathfrak{s}_{R}(m|n,r)$
. Now, by the triangular relation [Reference Du and Gu12, Theorem 7.4]:
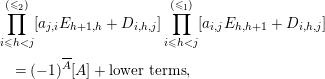 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{i\leqslant h<j}^{({\leqslant}_{2})}[a_{j,i}E_{h+1,h}+D_{i,h,j}]\mathop{\prod }_{i\leqslant h<j}^{({\leqslant}_{1})}[a_{i,j}E_{h,h+1}+D_{i,h,j}]\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{\overline{A}}[A]+\text{lower terms},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{i\leqslant h<j}^{({\leqslant}_{2})}[a_{j,i}E_{h+1,h}+D_{i,h,j}]\mathop{\prod }_{i\leqslant h<j}^{({\leqslant}_{1})}[a_{i,j}E_{h,h+1}+D_{i,h,j}]\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{\overline{A}}[A]+\text{lower terms},\end{eqnarray}$$
an inductive argument on the Bruhat order on
![]() $M(m|n,r)$
shows that every
$M(m|n,r)$
shows that every
![]() $[A]$
with
$[A]$
with
![]() $A\in M(m|n,r)_{l}$
belongs to
$A\in M(m|n,r)_{l}$
belongs to
![]() $\mathfrak{s}_{R}^{\prime }(m|n,r)$
. Hence,
$\mathfrak{s}_{R}^{\prime }(m|n,r)$
. Hence,
![]() $\mathfrak{s}_{R}(m|n,r)=\mathfrak{s}_{R}^{\prime }(m|n,r)$
is a subalgebra and, hence, a subsuperalgebra. From the argument above, we see easily that
$\mathfrak{s}_{R}(m|n,r)=\mathfrak{s}_{R}^{\prime }(m|n,r)$
is a subalgebra and, hence, a subsuperalgebra. From the argument above, we see easily that
![]() ${\rm \small{e}}_{h},{\rm \small{f}}_{h},1_{\unicode[STIX]{x1D706}}$
can be generators.
${\rm \small{e}}_{h},{\rm \small{f}}_{h},1_{\unicode[STIX]{x1D706}}$
can be generators.
Remarks 6.2. By [Reference Du, Gu and Wang14, Corollary 8.4],
![]() $\mathfrak{s}_{R}(m|n,r)$
is isomorphic to the infinitesimal
$\mathfrak{s}_{R}(m|n,r)$
is isomorphic to the infinitesimal
![]() $q$
-Schur superalgebra defined in [Reference Chen, Gu and Wang3, Section 3] by using quantum coordinate superalgebra.
$q$
-Schur superalgebra defined in [Reference Chen, Gu and Wang3, Section 3] by using quantum coordinate superalgebra.
We now construct a subsuperalgebra
![]() $\mathfrak{u}_{R}(m|n,r)$
. Let
$\mathfrak{u}_{R}(m|n,r)$
. Let
![]() $\mathbb{Z}_{l}:=\mathbb{Z}/l\mathbb{Z}$
and let
$\mathbb{Z}_{l}:=\mathbb{Z}/l\mathbb{Z}$
and let
![]() $\bar{\;}:\mathbb{Z}\rightarrow \mathbb{Z}_{l}$
be the quotient map. Extend this map to
$\bar{\;}:\mathbb{Z}\rightarrow \mathbb{Z}_{l}$
be the quotient map. Extend this map to
![]() $M(m|n,r)$
,
$M(m|n,r)$
,
![]() $\unicode[STIX]{x1D6EC}(m|n,r)$
by baring on the entries. Thus, we may identify the image
$\unicode[STIX]{x1D6EC}(m|n,r)$
by baring on the entries. Thus, we may identify the image
![]() $\overline{M(m|n,r)}$
with the following set:
$\overline{M(m|n,r)}$
with the following set:
where
![]() $A^{\pm }$
is obtained by replacing the diagonal of
$A^{\pm }$
is obtained by replacing the diagonal of
![]() $A$
with 0’s and
$A$
with 0’s and
![]() $\unicode[STIX]{x2202}_{A}\in \mathbb{Z}^{m+n}$
is the diagonal of
$\unicode[STIX]{x2202}_{A}\in \mathbb{Z}^{m+n}$
is the diagonal of
![]() $A$
(i.e.,
$A$
(i.e.,
![]() $A=A^{\pm }+\operatorname{diag}(\unicode[STIX]{x2202}_{A})$
). For
$A=A^{\pm }+\operatorname{diag}(\unicode[STIX]{x2202}_{A})$
). For
![]() $A=A^{\pm }+\operatorname{diag}(\overline{\unicode[STIX]{x2202}}_{A})\in \overline{M(m|n,r)}$
, define
$A=A^{\pm }+\operatorname{diag}(\overline{\unicode[STIX]{x2202}}_{A})\in \overline{M(m|n,r)}$
, define
and let
![]() $\overline{1}_{\unicode[STIX]{x1D706}}=\overline{\unicode[STIX]{x1D709}}_{\operatorname{diag}(\unicode[STIX]{x1D706})}$
. Note that every
$\overline{1}_{\unicode[STIX]{x1D706}}=\overline{\unicode[STIX]{x1D709}}_{\operatorname{diag}(\unicode[STIX]{x1D706})}$
. Note that every
![]() $\overline{\unicode[STIX]{x1D709}}_{A}$
is a homogeneous element with respect the super structure on
$\overline{\unicode[STIX]{x1D709}}_{A}$
is a homogeneous element with respect the super structure on
![]() ${\mathcal{S}}_{R}(m|n,r)$
.
${\mathcal{S}}_{R}(m|n,r)$
.
We now have the super analogue of the little
![]() $q$
-Schur algebra introduced in [Reference Du, Fu and Wang10].
$q$
-Schur algebra introduced in [Reference Du, Fu and Wang10].
Corollary 6.3. The subsuperspace
![]() $\mathfrak{u}_{R}(m|n,r)$
of
$\mathfrak{u}_{R}(m|n,r)$
of
![]() $\mathfrak{s}_{R}(m|n,r)$
spanned by
$\mathfrak{s}_{R}(m|n,r)$
spanned by
![]() $\overline{\unicode[STIX]{x1D709}}_{A}$
for all
$\overline{\unicode[STIX]{x1D709}}_{A}$
for all
![]() $A\in \overline{M(m|n,r)}$
is a subsuperalgebra with identity
$A\in \overline{M(m|n,r)}$
is a subsuperalgebra with identity
![]() $\sum _{x\in \overline{\unicode[STIX]{x1D6EC}(m|n,r)}}\overline{1}_{\operatorname{diag}(x)}$
and generated by
$\sum _{x\in \overline{\unicode[STIX]{x1D6EC}(m|n,r)}}\overline{1}_{\operatorname{diag}(x)}$
and generated by
![]() ${\rm \small{e}}_{h},{\rm \small{f}}_{h},\overline{1}_{\unicode[STIX]{x1D706}}$
for all
${\rm \small{e}}_{h},{\rm \small{f}}_{h},\overline{1}_{\unicode[STIX]{x1D706}}$
for all
![]() $1\leqslant h<m+n,\unicode[STIX]{x1D706}\in \overline{\unicode[STIX]{x1D6EC}(m|n,r)}$
.
$1\leqslant h<m+n,\unicode[STIX]{x1D706}\in \overline{\unicode[STIX]{x1D6EC}(m|n,r)}$
.
Proof. In this case, with a proof similar to that for Theorem 6.1, we see that
![]() $\mathfrak{u}_{R}(m|n,r)$
is the subalgebra generated by
$\mathfrak{u}_{R}(m|n,r)$
is the subalgebra generated by
![]() $\overline{\unicode[STIX]{x1D709}}_{aE_{h,h+1}+D}$
and
$\overline{\unicode[STIX]{x1D709}}_{aE_{h,h+1}+D}$
and
![]() $\overline{\unicode[STIX]{x1D709}}_{bE_{h+1,h}+D^{\prime }}$
, where
$\overline{\unicode[STIX]{x1D709}}_{bE_{h+1,h}+D^{\prime }}$
, where
![]() $D,D^{\prime }$
are diagonal matrices with
$D,D^{\prime }$
are diagonal matrices with
![]() $aE_{h,h+1}+D,bE_{h+1,h}+D^{\prime }\in \overline{M(m|n,r)}$
. Note that by taking the sum of the triangular relations (6.1.1) for every
$aE_{h,h+1}+D,bE_{h+1,h}+D^{\prime }\in \overline{M(m|n,r)}$
. Note that by taking the sum of the triangular relations (6.1.1) for every
![]() $A^{\pm }+\operatorname{diag}(\unicode[STIX]{x1D706})$
with
$A^{\pm }+\operatorname{diag}(\unicode[STIX]{x1D706})$
with
![]() $\overline{\unicode[STIX]{x1D706}}=\overline{\unicode[STIX]{x2202}}_{A}$
, we obtain the required triangular relation for
$\overline{\unicode[STIX]{x1D706}}=\overline{\unicode[STIX]{x2202}}_{A}$
, we obtain the required triangular relation for
![]() $\overline{\unicode[STIX]{x1D709}}_{A}$
’s (cf. the proof of [Reference Du and Gu12, Theorem 8.1]). The last assertion is clear as every
$\overline{\unicode[STIX]{x1D709}}_{A}$
’s (cf. the proof of [Reference Du and Gu12, Theorem 8.1]). The last assertion is clear as every
![]() $\overline{\unicode[STIX]{x1D709}}_{aE_{h,h+1}+D}$
or
$\overline{\unicode[STIX]{x1D709}}_{aE_{h,h+1}+D}$
or
![]() $\overline{\unicode[STIX]{x1D709}}_{bE_{h+1,h}+D^{\prime }}$
has the form
$\overline{\unicode[STIX]{x1D709}}_{bE_{h+1,h}+D^{\prime }}$
has the form
![]() ${\rm \small{e}}_{h}^{(a)}\bar{1}_{\unicode[STIX]{x1D706}}$
or
${\rm \small{e}}_{h}^{(a)}\bar{1}_{\unicode[STIX]{x1D706}}$
or
![]() ${\rm \small{f}}_{h}^{(b)}\bar{1}_{\unicode[STIX]{x1D706}}$
.
${\rm \small{f}}_{h}^{(b)}\bar{1}_{\unicode[STIX]{x1D706}}$
.
We end the paper with the following semisimplicity criteria for the infinitesimal/little
![]() $q$
-Schur superalgebras; compare the nonsuper case [Reference Du, Fu and Wang11, Section 7] and [Reference Fu21].
$q$
-Schur superalgebras; compare the nonsuper case [Reference Du, Fu and Wang11, Section 7] and [Reference Fu21].
Theorem 6.4. The superalgebra
![]() $\mathfrak{s}_{F}(m|n,r)$
or
$\mathfrak{s}_{F}(m|n,r)$
or
![]() $\mathfrak{u}_{F}(m|n,r)$
with
$\mathfrak{u}_{F}(m|n,r)$
with
![]() $m,n\geqslant 1$
is semisimple if and only if one of the following holds:
$m,n\geqslant 1$
is semisimple if and only if one of the following holds:
(1)
 $r<l$
;
$r<l$
;(2)
 $m=n=1,l\nmid r$
.
$m=n=1,l\nmid r$
.
Proof. We first look at the “infinitesimal” case. We observe that, if
![]() $r<l$
or
$r<l$
or
![]() $m=n=1$
, then
$m=n=1$
, then
![]() $\mathfrak{s}_{F}(m|n,r)={\mathcal{S}}_{F}(m|n,r)$
. The “if” part is clear. Conversely, suppose
$\mathfrak{s}_{F}(m|n,r)={\mathcal{S}}_{F}(m|n,r)$
. The “if” part is clear. Conversely, suppose
![]() $\mathfrak{s}_{F}(m|n,r)$
is semisimple. Since
$\mathfrak{s}_{F}(m|n,r)$
is semisimple. Since
![]() $\mathfrak{s}_{F}(1|1,r)={\mathcal{S}}_{F}(1|1,r)$
, its semisimplicity forces
$\mathfrak{s}_{F}(1|1,r)={\mathcal{S}}_{F}(1|1,r)$
, its semisimplicity forces
![]() $l\nmid r$
. Assume
$l\nmid r$
. Assume
![]() $m\geqslant 2,n\geqslant 1$
and
$m\geqslant 2,n\geqslant 1$
and
![]() $l\leqslant r$
. By the proof of Lemma 5.3, we see that
$l\leqslant r$
. By the proof of Lemma 5.3, we see that
![]() $\mathfrak{s}_{F}(2|1,r)e$
(
$\mathfrak{s}_{F}(2|1,r)e$
(
![]() $e=1_{(r,0,0)}$
) is indecomposable and contains the proper submodule
$e=1_{(r,0,0)}$
) is indecomposable and contains the proper submodule
![]() $\mathfrak{s}_{F}(2|1,r)[A_{al,b,0}]$
if
$\mathfrak{s}_{F}(2|1,r)[A_{al,b,0}]$
if
![]() $l\nmid r+1$
, or
$l\nmid r+1$
, or
![]() $\mathfrak{s}_{F}(2|1,r)[A_{r-l,l-1,1}]$
if
$\mathfrak{s}_{F}(2|1,r)[A_{r-l,l-1,1}]$
if
![]() $l\mid r+1$
. Hence, we can use the Schur functor argument to conclude
$l\mid r+1$
. Hence, we can use the Schur functor argument to conclude
![]() $\mathfrak{s}_{F}(m|n,r)$
is not semisimple unless
$\mathfrak{s}_{F}(m|n,r)$
is not semisimple unless
![]() $r<l$
.
$r<l$
.
We now look at the “little” case. If
![]() $r<l$
, then
$r<l$
, then
![]() $\mathfrak{u}_{F}(m|n,r)={\mathcal{S}}_{F}(m|n,r)$
is semisimple. If
$\mathfrak{u}_{F}(m|n,r)={\mathcal{S}}_{F}(m|n,r)$
is semisimple. If
![]() $m=n=1$
and
$m=n=1$
and
![]() $l\nmid r$
, then the simple module
$l\nmid r$
, then the simple module
![]() $L(a)$
constructed in the proof of Lemma 5.1 remains irreducible when restricted to
$L(a)$
constructed in the proof of Lemma 5.1 remains irreducible when restricted to
![]() $\mathfrak{u}_{F}(m|n,r)$
. This is seen from the last assertion of Corollary 6.3. Thus,
$\mathfrak{u}_{F}(m|n,r)$
. This is seen from the last assertion of Corollary 6.3. Thus,
![]() $\mathfrak{s}_{F}(m|n,r)$
as an
$\mathfrak{s}_{F}(m|n,r)$
as an
![]() $\mathfrak{u}_{F}(m|n,r)$
-module is semisimple. As a
$\mathfrak{u}_{F}(m|n,r)$
-module is semisimple. As a
![]() $\mathfrak{u}_{F}(m|n,r)$
-submodule of
$\mathfrak{u}_{F}(m|n,r)$
-submodule of
![]() $\mathfrak{s}_{F}(m|n,r)$
,
$\mathfrak{s}_{F}(m|n,r)$
,
![]() $\mathfrak{u}_{F}(m|n,r)$
is semisimple. Conversely, if conditions (1) and (2) both fail. Then
$\mathfrak{u}_{F}(m|n,r)$
is semisimple. Conversely, if conditions (1) and (2) both fail. Then
![]() $r\geqslant l$
. If one of the
$r\geqslant l$
. If one of the
![]() $m$
and
$m$
and
![]() $n$
is great than 1, then
$n$
is great than 1, then
![]() $\mathfrak{u}_{F}(m|n,r)$
is not semisimple. To see this, it is enough to show that
$\mathfrak{u}_{F}(m|n,r)$
is not semisimple. To see this, it is enough to show that
![]() $M=\mathfrak{s}_{F}(2|1,r)e$
as an
$M=\mathfrak{s}_{F}(2|1,r)e$
as an
![]() $\mathfrak{u}_{F}(2|1,r)$
-module is indecomposable. Indeed, suppose
$\mathfrak{u}_{F}(2|1,r)$
-module is indecomposable. Indeed, suppose
![]() $M=M_{1}\oplus M_{2}$
where
$M=M_{1}\oplus M_{2}$
where
![]() $M_{i}$
are nonzero
$M_{i}$
are nonzero
![]() $\mathfrak{u}_{F}(2|1,r)$
-submodules. Then, for any
$\mathfrak{u}_{F}(2|1,r)$
-submodules. Then, for any
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
,
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}(m|n,r)$
,
![]() $1_{\unicode[STIX]{x1D706}}M_{1}$
and
$1_{\unicode[STIX]{x1D706}}M_{1}$
and
![]() $1_{\unicode[STIX]{x1D706}}M_{2}$
cannot be both nonzero since
$1_{\unicode[STIX]{x1D706}}M_{2}$
cannot be both nonzero since
![]() $\dim 1_{\unicode[STIX]{x1D706}}M=1$
. This shows that
$\dim 1_{\unicode[STIX]{x1D706}}M=1$
. This shows that
![]() $M_{i}$
is a direct sum of some
$M_{i}$
is a direct sum of some
![]() $1_{\unicode[STIX]{x1D706}}M$
. Hence,
$1_{\unicode[STIX]{x1D706}}M$
. Hence,
![]() $M_{i}$
is an
$M_{i}$
is an
![]() $\mathfrak{s}_{F}(2|1,r)$
-module, contrary to the fact that
$\mathfrak{s}_{F}(2|1,r)$
-module, contrary to the fact that
![]() $M$
is an indecomposable
$M$
is an indecomposable
![]() $\mathfrak{s}_{F}(2|1,r)$
-module. If
$\mathfrak{s}_{F}(2|1,r)$
-module. If
![]() $m=n=1$
, then
$m=n=1$
, then
![]() $l\mid r$
. In this case,
$l\mid r$
. In this case,
![]() $\mathfrak{u}_{F}(1|1,r)$
is clearly non-semsimple as
$\mathfrak{u}_{F}(1|1,r)$
is clearly non-semsimple as
![]() $\mathfrak{u}_{F}(1|1,r)\overline{1}_{0}$
is indecomposable, but not irreducible.
$\mathfrak{u}_{F}(1|1,r)\overline{1}_{0}$
is indecomposable, but not irreducible.
Acknowledgments
We thank the referee for several helpful comments.
Appendix A. A Theorem of Erdmann–Nakano
Theorem A.1. [Reference Erdmann and Nakano18, Section 1.3, Theorem (A)]
Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $p\geqslant 0$
containing elements
$p\geqslant 0$
containing elements
![]() $q\neq 0,1$
. Then the
$q\neq 0,1$
. Then the
![]() $q$
-Schur algebra
$q$
-Schur algebra
![]() ${\mathcal{S}}_{F}(m,r)$
is semisimple if and only if one of the following holds:
${\mathcal{S}}_{F}(m,r)$
is semisimple if and only if one of the following holds:
(1)
 $q$
is not a root of unity;
$q$
is not a root of unity;(2)
 $q$
is a primitive
$q$
is a primitive
 $l$
th root of unity and
$l$
th root of unity and
 $r<l$
;
$r<l$
;(3)
 $m=2,p=0,l=2$
and
$m=2,p=0,l=2$
and
 $r$
is odd;
$r$
is odd;(4)
 $m=2,p\geqslant 3,l=2$
and
$m=2,p\geqslant 3,l=2$
and
 $r$
is odd with
$r$
is odd with
 $r<2p+1$
.
$r<2p+1$
.
Proof. If
![]() $q$
satisfies (1) or (2), then
$q$
satisfies (1) or (2), then
![]() ${\mathcal{S}}_{F}(m,r)$
is clearly semisimple. Suppose now that
${\mathcal{S}}_{F}(m,r)$
is clearly semisimple. Suppose now that
![]() $q$
is a primitive
$q$
is a primitive
![]() $l$
th root of unity and
$l$
th root of unity and
![]() $r\geqslant l>1$
. By Corollary 4.2, an argument similar to those given in the proofs of Lemma 5.3 and Theorem 5.4 shows that both
$r\geqslant l>1$
. By Corollary 4.2, an argument similar to those given in the proofs of Lemma 5.3 and Theorem 5.4 shows that both
![]() ${\mathcal{S}}_{F}(m,r)1_{(r,0,\ldots ,0)},m\geqslant 3$
, and
${\mathcal{S}}_{F}(m,r)1_{(r,0,\ldots ,0)},m\geqslant 3$
, and
![]() ${\mathcal{S}}_{F}(2,r)1_{(r,0)},l\nmid r+1$
, are indecomposable but not irreducible. In particular, both
${\mathcal{S}}_{F}(2,r)1_{(r,0)},l\nmid r+1$
, are indecomposable but not irreducible. In particular, both
![]() ${\mathcal{S}}_{F}(2,l)$
and
${\mathcal{S}}_{F}(2,l)$
and
![]() ${\mathcal{S}}_{F}(2,l+1)$
are not semisimple if
${\mathcal{S}}_{F}(2,l+1)$
are not semisimple if
![]() $l\geqslant 3$
. Since tensoring an
$l\geqslant 3$
. Since tensoring an
![]() ${\mathcal{S}}_{F}(2,r)$
-module with the determinant representation gives an
${\mathcal{S}}_{F}(2,r)$
-module with the determinant representation gives an
![]() ${\mathcal{S}}_{F}(2,r+2)$
-module, we see that
${\mathcal{S}}_{F}(2,r+2)$
-module, we see that
![]() ${\mathcal{S}}_{F}(2,r)$
is not semisimple for all
${\mathcal{S}}_{F}(2,r)$
is not semisimple for all
![]() $r\geqslant l\geqslant 3$
. Hence, a semisimple
$r\geqslant l\geqslant 3$
. Hence, a semisimple
![]() ${\mathcal{S}}_{F}(m,r)$
forces
${\mathcal{S}}_{F}(m,r)$
forces
![]() $m=2,l=2$
and
$m=2,l=2$
and
![]() $2|r+1$
. It remains to determine the semisimplicity of
$2|r+1$
. It remains to determine the semisimplicity of
![]() ${\mathcal{S}}_{F}(2,r)$
when
${\mathcal{S}}_{F}(2,r)$
when
![]() $r\geqslant l=2$
and
$r\geqslant l=2$
and
![]() $r$
odd (and so
$r$
odd (and so
![]() $2|r+1$
). We claim that, for
$2|r+1$
). We claim that, for
![]() $r\geqslant l=2$
with
$r\geqslant l=2$
with
![]() $r$
odd,
$r$
odd,
![]() ${\mathcal{S}}_{F}(2,r)$
is semisimple if and only if either
${\mathcal{S}}_{F}(2,r)$
is semisimple if and only if either
![]() $p=0$
or
$p=0$
or
![]() $p\geqslant 3$
but
$p\geqslant 3$
but
![]() $r<2p+1$
. Indeed,
$r<2p+1$
. Indeed,
![]() ${\mathcal{S}}_{F}(2,r)$
is semisimple if and only if all
${\mathcal{S}}_{F}(2,r)$
is semisimple if and only if all
![]() $q$
-Weyl modules
$q$
-Weyl modules
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
, are irreducible. For
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706}),\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
, are irreducible. For
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
, if
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
, if
![]() $x_{\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is a highest weight vector, then
$x_{\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is a highest weight vector, then
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
has a basis
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
has a basis
![]() $x_{\unicode[STIX]{x1D706}},{\rm \small{f}}_{1}x_{\unicode[STIX]{x1D706}},{\rm \small{f}}_{1}^{(2)}x_{\unicode[STIX]{x1D706}},\ldots ,{\rm \small{f}}_{1}^{(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2})}x_{\unicode[STIX]{x1D706}}$
and, for
$x_{\unicode[STIX]{x1D706}},{\rm \small{f}}_{1}x_{\unicode[STIX]{x1D706}},{\rm \small{f}}_{1}^{(2)}x_{\unicode[STIX]{x1D706}},\ldots ,{\rm \small{f}}_{1}^{(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2})}x_{\unicode[STIX]{x1D706}}$
and, for
![]() $1\leqslant a\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
, we have
$1\leqslant a\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
, we have
where
![]() $\unicode[STIX]{x1D710}=\sqrt{q}$
. Thus, the irreducibility of
$\unicode[STIX]{x1D710}=\sqrt{q}$
. Thus, the irreducibility of
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is equivalent to
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is equivalent to
Since
![]() $r=\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}$
is odd and
$r=\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}$
is odd and
![]() $l=2$
, we see that
$l=2$
, we see that
![]() $\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
is also odd and
$\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
is also odd and
where
![]() $a=2a_{1}+a_{0}$
with
$a=2a_{1}+a_{0}$
with
![]() $a_{0}=0,1.$
Obviously,
$a_{0}=0,1.$
Obviously,
![]() $\left[{1\atop a_{0}}\right]_{\unicode[STIX]{x1D710}}=1.$
Thus, if
$\left[{1\atop a_{0}}\right]_{\unicode[STIX]{x1D710}}=1.$
Thus, if
![]() $p=0$
or
$p=0$
or
![]() $p\geqslant 3$
but
$p\geqslant 3$
but
![]() $r<2p+1$
then
$r<2p+1$
then
![]() $\left(\begin{smallmatrix}\frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}-1}{2}\\ a_{1}\end{smallmatrix}\right)\neq 0$
for all
$\left(\begin{smallmatrix}\frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}-1}{2}\\ a_{1}\end{smallmatrix}\right)\neq 0$
for all
![]() $(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
and
$(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})\in \unicode[STIX]{x1D6EC}^{+}(2,r)$
and
![]() $1\leqslant a\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
. Hence,
$1\leqslant a\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
. Hence,
![]() ${\mathcal{S}}_{F}(2,r)$
is semisimple in this case. Conversely, if
${\mathcal{S}}_{F}(2,r)$
is semisimple in this case. Conversely, if
![]() $r\geqslant 2p+1,$
choose
$r\geqslant 2p+1,$
choose
![]() $\unicode[STIX]{x1D706}$
so that
$\unicode[STIX]{x1D706}$
so that
![]() $\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}=2p+1$
and
$\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}=2p+1$
and
![]() $a=3$
. Then
$a=3$
. Then
Hence,
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is not simple in this case and so
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$
is not simple in this case and so
![]() ${\mathcal{S}}_{F}(2,r)$
is not semisimple.
${\mathcal{S}}_{F}(2,r)$
is not semisimple.