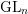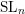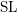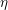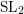Introduction
A number of cohomology theories refining
![]() $K$
-theory and motivic cohomology have been introduced and studied over the past 20 years. Well-known examples include hermitian
$K$
-theory and motivic cohomology have been introduced and studied over the past 20 years. Well-known examples include hermitian
![]() $K$
-theory [Reference Karoubi and Villamayor21, Reference Schlichting36], the theory of the Chow–Witt groups [Reference Asok and Fasel4, Reference Barge and Morel7, Reference Fasel15, Reference Fasel and Srinivas17], Milnor–Witt motivic cohomology [Reference Bachmann and Fasel6, Reference Calmès and Fasel10, Reference Déglise and Fasel12–Reference Druzhinin14], Witt theory and the cohomology of the Witt sheaves [Reference Ananyevskiy3]. All these theories have the property of being SL-oriented, that is, there are Thom classes for vector bundles endowed with a trivialization of the determinant line bundle. Witt theory and the cohomology of the Witt sheaves have the additional property of being
$K$
-theory [Reference Karoubi and Villamayor21, Reference Schlichting36], the theory of the Chow–Witt groups [Reference Asok and Fasel4, Reference Barge and Morel7, Reference Fasel15, Reference Fasel and Srinivas17], Milnor–Witt motivic cohomology [Reference Bachmann and Fasel6, Reference Calmès and Fasel10, Reference Déglise and Fasel12–Reference Druzhinin14], Witt theory and the cohomology of the Witt sheaves [Reference Ananyevskiy3]. All these theories have the property of being SL-oriented, that is, there are Thom classes for vector bundles endowed with a trivialization of the determinant line bundle. Witt theory and the cohomology of the Witt sheaves have the additional property of being
![]() $\unicode[STIX]{x1D702}$
-invertible, that is multiplication by the algebraic Hopf map
$\unicode[STIX]{x1D702}$
-invertible, that is multiplication by the algebraic Hopf map
![]() $\unicode[STIX]{x1D702}$
is an isomorphism on the theory.
$\unicode[STIX]{x1D702}$
is an isomorphism on the theory.
The
![]() $\operatorname{SL}$
-oriented,
$\operatorname{SL}$
-oriented,
![]() $\unicode[STIX]{x1D702}$
-invertible theories
$\unicode[STIX]{x1D702}$
-invertible theories
![]() ${\mathcal{E}}$
have been studied by Ananyevskiy [Reference Ananyevskiy3]. He computes the
${\mathcal{E}}$
have been studied by Ananyevskiy [Reference Ananyevskiy3]. He computes the
![]() ${\mathcal{E}}$
-cohomology of
${\mathcal{E}}$
-cohomology of
![]() $\operatorname{BSL}_{n}$
and proves a fundamental
$\operatorname{BSL}_{n}$
and proves a fundamental
![]() $\operatorname{SL}_{2}$
-splitting principle, replacing the classical
$\operatorname{SL}_{2}$
-splitting principle, replacing the classical
![]() $\mathbb{G}_{m}$
-splitting principle which plays a central role in the calculus of characteristic classes in
$\mathbb{G}_{m}$
-splitting principle which plays a central role in the calculus of characteristic classes in
![]() $\operatorname{GL}$
-oriented theories such as
$\operatorname{GL}$
-oriented theories such as
![]() $K$
-theory, motivic cohomology or
$K$
-theory, motivic cohomology or
![]() $\operatorname{MGL}$
-theory.
$\operatorname{MGL}$
-theory.
Works by Hoyois [Reference Hoyois18] and Kass–Wickelgren [Reference Kass and Wickelgren22, Reference Kass and Wickelgren23], as well as our papers [Reference Levine24, Reference Levine25], have initiated a study of Euler characteristics and Euler classes with values in the Grothendieck–Witt ring or in the Chow–Witt groups. In this paper we continue this study, looking at Euler characteristics and characteristic classes with values in Witt cohomology and other
![]() $\operatorname{SL}$
-oriented
$\operatorname{SL}$
-oriented
![]() $\unicode[STIX]{x1D702}$
-invertible theories.
$\unicode[STIX]{x1D702}$
-invertible theories.
Using the six-functor formalism on the motivic stable homotopy category, we define a motivic version of the Becker–Gottlieb transfer. This includes the case of a Nisnevich locally trivial fiber bundle
![]() $f:E\rightarrow B$
with fiber
$f:E\rightarrow B$
with fiber
![]() $F$
, such that the suspension spectrum of
$F$
, such that the suspension spectrum of
![]() $F$
is a strongly dualizable object in the appropriate motivic stable homotopy category. Just as for the classical Becker–Gottlieb transfer, the motivic transfer defines a splitting to the pullback map
$F$
is a strongly dualizable object in the appropriate motivic stable homotopy category. Just as for the classical Becker–Gottlieb transfer, the motivic transfer defines a splitting to the pullback map
![]() $f^{\ast }$
on
$f^{\ast }$
on
![]() ${\mathcal{E}}$
-cohomology for a motivic spectrum
${\mathcal{E}}$
-cohomology for a motivic spectrum
![]() ${\mathcal{E}}$
, as long as the categorical Euler characteristic of
${\mathcal{E}}$
, as long as the categorical Euler characteristic of
![]() $F$
is invertible in the coefficient ring of
$F$
is invertible in the coefficient ring of
![]() ${\mathcal{E}}$
. This is discussed in Section 1.
${\mathcal{E}}$
. This is discussed in Section 1.
In Section 2, we consider a conjecture of Morel that for
![]() $N$
the normalizer of a maximal torus in a split reductive group
$N$
the normalizer of a maximal torus in a split reductive group
![]() $G$
over a perfect field
$G$
over a perfect field
![]() $k$
, the quotient scheme
$k$
, the quotient scheme
![]() $N\backslash G$
has Euler characteristic one in the Grothendieck–Witt ring of
$N\backslash G$
has Euler characteristic one in the Grothendieck–Witt ring of
![]() $k$
. This generalizes the fact that, for
$k$
. This generalizes the fact that, for
![]() $N$
the normalizer of a maximal torus in a reductive complex Lie group
$N$
the normalizer of a maximal torus in a reductive complex Lie group
![]() $G$
,
$G$
,
![]() $N\backslash G$
has topological Euler characteristic one. We verify a weak form of this conjecture for
$N\backslash G$
has topological Euler characteristic one. We verify a weak form of this conjecture for
![]() $\operatorname{GL}_{n}$
and
$\operatorname{GL}_{n}$
and
![]() $\operatorname{SL}_{n}$
over a characteristic zero field, as well as the strong form for
$\operatorname{SL}_{n}$
over a characteristic zero field, as well as the strong form for
![]() $\operatorname{GL}_{2}$
and
$\operatorname{GL}_{2}$
and
![]() $\operatorname{SL}_{2}$
over an arbitrary perfect field.
$\operatorname{SL}_{2}$
over an arbitrary perfect field.
We recall the results of Ananyevskiy that we will be using here in Section 3. In Section 4, we reduce the computation of characteristic classes in an
![]() $\unicode[STIX]{x1D702}$
-invertible,
$\unicode[STIX]{x1D702}$
-invertible,
![]() $\operatorname{SL}$
-oriented theory (satisfying an additional technical hypothesis, see Theorem 4.1 for the precise statement) from the general case to that of bundles with trivialized determinant.
$\operatorname{SL}$
-oriented theory (satisfying an additional technical hypothesis, see Theorem 4.1 for the precise statement) from the general case to that of bundles with trivialized determinant.
Ananyevskiy’s splitting principle for
![]() $\operatorname{SL}_{n}$
-bundles reduces the computation of characteristic classes for such bundles in
$\operatorname{SL}_{n}$
-bundles reduces the computation of characteristic classes for such bundles in
![]() $\operatorname{SL}$
-oriented,
$\operatorname{SL}$
-oriented,
![]() $\unicode[STIX]{x1D702}$
-invertible theories
$\unicode[STIX]{x1D702}$
-invertible theories
![]() ${\mathcal{E}}$
to the case of
${\mathcal{E}}$
to the case of
![]() $\operatorname{SL}_{2}$
-bundles. In Sections 5 and 6 we look more closely at
$\operatorname{SL}_{2}$
-bundles. In Sections 5 and 6 we look more closely at
![]() $\operatorname{SL}_{2}$
, refining Ananyevskiy’s splitting principle to reduce further to bundles with group the normalizer
$\operatorname{SL}_{2}$
, refining Ananyevskiy’s splitting principle to reduce further to bundles with group the normalizer
![]() $N_{\operatorname{SL}_{2}}(T)$
of the standard torus
$N_{\operatorname{SL}_{2}}(T)$
of the standard torus
![]() $T$
in
$T$
in
![]() $\operatorname{SL}_{2}$
. This makes computations much easier, as an irreducible representation of
$\operatorname{SL}_{2}$
. This makes computations much easier, as an irreducible representation of
![]() $N_{\operatorname{SL}_{2}}(T)$
has dimension either one or two, and the representation theory of
$N_{\operatorname{SL}_{2}}(T)$
has dimension either one or two, and the representation theory of
![]() $N_{\operatorname{SL}_{2}}(T)$
is formally (almost) the same as that of real
$N_{\operatorname{SL}_{2}}(T)$
is formally (almost) the same as that of real
![]() $O(2)$
-bundles. In Section 6 we introduce the rank two bundles
$O(2)$
-bundles. In Section 6 we introduce the rank two bundles
![]() $\tilde{O} (m)$
over
$\tilde{O} (m)$
over
![]() $BN_{\operatorname{SL}_{2}}(T)$
, as analogs of the classical bundles
$BN_{\operatorname{SL}_{2}}(T)$
, as analogs of the classical bundles
![]() $O(m)$
on
$O(m)$
on
![]() $B\mathbb{G}_{m}$
, and show that the analogy gives a method for computing of the Euler class in Witt cohomology. We apply these considerations in Section 7 to carry out our computation of the Euler class and Pontryagin class of
$B\mathbb{G}_{m}$
, and show that the analogy gives a method for computing of the Euler class in Witt cohomology. We apply these considerations in Section 7 to carry out our computation of the Euler class and Pontryagin class of
![]() $\tilde{O} (m)$
in Theorem 7.1. This is used in Section 8 to compute the characteristic classes in Witt cohomology of symmetric powers of a rank two bundle, see Theorem 8.1.
$\tilde{O} (m)$
in Theorem 7.1. This is used in Section 8 to compute the characteristic classes in Witt cohomology of symmetric powers of a rank two bundle, see Theorem 8.1.
We compute the characteristic classes in Witt cohomology for tensor products in Section 9, which together with Ananyevskiy’s splitting principle and our computation of the characteristic classes of symmetric powers of a rank two bundle gives a complete calculus for the characteristic classes in Witt cohomology. We conclude with an example, computing the “quadratic count” of lines on a smooth hypersurface of degree
![]() $2d-1$
in
$2d-1$
in
![]() $\mathbb{P}^{d+1}$
. This recovers results of Kass–Wickelgren for cubic surfaces [Reference Kass and Wickelgren23] and gives a purely algebraic treatment of some results of Okonek–Teleman [Reference Okonek and Teleman33].
$\mathbb{P}^{d+1}$
. This recovers results of Kass–Wickelgren for cubic surfaces [Reference Kass and Wickelgren23] and gives a purely algebraic treatment of some results of Okonek–Teleman [Reference Okonek and Teleman33].
We would like to thank Eva Bayer, Jesse Kass and Kirsten Wickelgren for their comments and suggestions. Eva Bayer drew our attention to Serre’s theorem on computing Hasse–Witt invariants of trace forms, and pointed out several other facts about quadratic forms, such as her paper with Suarez [Reference Bayer-Fluckiger and Suarez8], which were all very important for computing the Euler characteristic of the bundles
![]() $\tilde{O} (m)$
, especially our Lemma 7.3. We also thank the referee for making a number of very helpful comments and suggestions.
$\tilde{O} (m)$
, especially our Lemma 7.3. We also thank the referee for making a number of very helpful comments and suggestions.
1 Becker–Gottlieb transfers
We fix a Noetherian base scheme
![]() $S$
and let
$S$
and let
![]() $\mathbf{Sch}/S$
denote the category of finite type separated
$\mathbf{Sch}/S$
denote the category of finite type separated
![]() $S$
-schemes.
$S$
-schemes.
We have the motivic stable homotopy category
where
![]() $\mathbf{Tr}$
is the 2-category of symmetric monoidal triangulated categories. Following [Reference Ayoub5, Reference Cisinski and Déglise11, Reference Hoyois19], the functor
$\mathbf{Tr}$
is the 2-category of symmetric monoidal triangulated categories. Following [Reference Ayoub5, Reference Cisinski and Déglise11, Reference Hoyois19], the functor
![]() $\operatorname{SH}(-)$
admits the Grothendieck six operations; we briefly review the aspects of this structure that we will be needing here. We note that the theory in [Reference Ayoub5, Reference Hoyois19] is for quasi-projective
$\operatorname{SH}(-)$
admits the Grothendieck six operations; we briefly review the aspects of this structure that we will be needing here. We note that the theory in [Reference Ayoub5, Reference Hoyois19] is for quasi-projective
![]() $S$
-schemes; the extension to separated
$S$
-schemes; the extension to separated
![]() $S$
-schemes of finite type is accomplished in [Reference Cisinski and Déglise11, Theorem 2.4.50].
$S$
-schemes of finite type is accomplished in [Reference Cisinski and Déglise11, Theorem 2.4.50].
For each
![]() $X$
,
$X$
,
![]() $\operatorname{SH}(X)$
is the homotopy category of a closed symmetric stable model category [Reference Jardine20], which makes
$\operatorname{SH}(X)$
is the homotopy category of a closed symmetric stable model category [Reference Jardine20], which makes
![]() $\operatorname{SH}(X)$
into a closed symmetric monoidal category. We denote the symmetric monoidal product in
$\operatorname{SH}(X)$
into a closed symmetric monoidal category. We denote the symmetric monoidal product in
![]() $\operatorname{SH}(X)$
by
$\operatorname{SH}(X)$
by
![]() $\wedge _{X}$
and the adjoint internal Hom by
$\wedge _{X}$
and the adjoint internal Hom by
![]() ${\mathcal{H}}om_{X}(-,-)$
. The unit
${\mathcal{H}}om_{X}(-,-)$
. The unit
![]() $1_{X}$
is the motivic sphere spectrum over
$1_{X}$
is the motivic sphere spectrum over
![]() $X$
,
$X$
,
![]() $\mathbb{S}_{X}$
. We have for each morphism
$\mathbb{S}_{X}$
. We have for each morphism
![]() $f:X\rightarrow Y$
in
$f:X\rightarrow Y$
in
![]() $\mathbf{Sch}/S$
the exact symmetric monoidal functor
$\mathbf{Sch}/S$
the exact symmetric monoidal functor
![]() $f^{\ast }:\operatorname{SH}(Y)\rightarrow \operatorname{SH}(X)$
with right adjoint
$f^{\ast }:\operatorname{SH}(Y)\rightarrow \operatorname{SH}(X)$
with right adjoint
![]() $f_{\ast }:\operatorname{SH}(X)\rightarrow \operatorname{SH}(Y)$
, and exact functors
$f_{\ast }:\operatorname{SH}(X)\rightarrow \operatorname{SH}(Y)$
, and exact functors
![]() $f^{!}:\operatorname{SH}(Y)\rightarrow \operatorname{SH}(X)$
,
$f^{!}:\operatorname{SH}(Y)\rightarrow \operatorname{SH}(X)$
,
![]() $f_{!}:\operatorname{SH}(X)\rightarrow \operatorname{SH}(Y)$
, with
$f_{!}:\operatorname{SH}(X)\rightarrow \operatorname{SH}(Y)$
, with
![]() $f_{!}$
left adjoint to
$f_{!}$
left adjoint to
![]() $f^{!}$
.
$f^{!}$
.
We refer to a commutative monoid
![]() ${\mathcal{E}}$
in the symmetric monoidal category
${\mathcal{E}}$
in the symmetric monoidal category
![]() $\operatorname{SH}(X)$
as a motivic ring spectrum, that is,
$\operatorname{SH}(X)$
as a motivic ring spectrum, that is,
![]() ${\mathcal{E}}$
is endowed with a multiplication map
${\mathcal{E}}$
is endowed with a multiplication map
![]() $\unicode[STIX]{x1D707}:{\mathcal{E}}\wedge _{X}{\mathcal{E}}\rightarrow {\mathcal{E}}$
and a unit map
$\unicode[STIX]{x1D707}:{\mathcal{E}}\wedge _{X}{\mathcal{E}}\rightarrow {\mathcal{E}}$
and a unit map
![]() $e:1_{X}\rightarrow {\mathcal{E}}$
such that
$e:1_{X}\rightarrow {\mathcal{E}}$
such that
![]() $({\mathcal{E}},\unicode[STIX]{x1D707},e)$
is a commutative monoid in
$({\mathcal{E}},\unicode[STIX]{x1D707},e)$
is a commutative monoid in
![]() $(\operatorname{SH}(X),\wedge _{X},1_{X})$
.
$(\operatorname{SH}(X),\wedge _{X},1_{X})$
.
The adjoint pair
![]() $f_{!}\dashv f^{!}$
satisfies a projection formula and the adjunctions extend to internal adjunctions: for
$f_{!}\dashv f^{!}$
satisfies a projection formula and the adjunctions extend to internal adjunctions: for
![]() $f:X\rightarrow Y$
, there are natural isomorphisms
$f:X\rightarrow Y$
, there are natural isomorphisms
There is a natural transformation
![]() $\unicode[STIX]{x1D702}_{!\ast }^{f}:f_{!}\rightarrow f_{\ast }$
, which is an isomorphism if
$\unicode[STIX]{x1D702}_{!\ast }^{f}:f_{!}\rightarrow f_{\ast }$
, which is an isomorphism if
![]() $f$
is proper (see e.g. [Reference Cisinski and Déglise11, Section 2.2.6]). Furthermore, for
$f$
is proper (see e.g. [Reference Cisinski and Déglise11, Section 2.2.6]). Furthermore, for
![]() $f$
smooth, the functor
$f$
smooth, the functor
![]() $f^{\ast }$
admits a left adjoint
$f^{\ast }$
admits a left adjoint
![]() $f_{\#}$
.
$f_{\#}$
.
If
![]() $i:X\rightarrow Y$
is a closed immersion with open complement
$i:X\rightarrow Y$
is a closed immersion with open complement
![]() $j:U\rightarrow Y$
, there are localization distinguished triangles
$j:U\rightarrow Y$
, there are localization distinguished triangles
and
In addition,
![]() $j_{!}=j_{\#}$
,
$j_{!}=j_{\#}$
,
![]() $j^{!}=j^{\ast }$
and
$j^{!}=j^{\ast }$
and
![]() $i_{!}=i_{\ast }$
, the counit
$i_{!}=i_{\ast }$
, the counit
![]() $i^{\ast }i_{\ast }\rightarrow \text{Id}$
is an isomorphism and the pair
$i^{\ast }i_{\ast }\rightarrow \text{Id}$
is an isomorphism and the pair
![]() $(i^{\ast },j^{\ast })$
is conservative. This gives the following weak Nisnevich descent property: let
$(i^{\ast },j^{\ast })$
is conservative. This gives the following weak Nisnevich descent property: let
![]() $\{g_{i}:U_{i}\rightarrow Y\}$
be a Nisnevich cover. A morphism
$\{g_{i}:U_{i}\rightarrow Y\}$
be a Nisnevich cover. A morphism
![]() $f:a\rightarrow b$
in
$f:a\rightarrow b$
in
![]() $\operatorname{SH}(Y)$
is an isomorphism if and only if
$\operatorname{SH}(Y)$
is an isomorphism if and only if
![]() $g_{i}^{\ast }f:g_{i}^{\ast }a\rightarrow g_{i}^{\ast }b$
is an isomorphism in
$g_{i}^{\ast }f:g_{i}^{\ast }a\rightarrow g_{i}^{\ast }b$
is an isomorphism in
![]() $\operatorname{SH}(U_{i})$
for all
$\operatorname{SH}(U_{i})$
for all
![]() $i$
(see [Reference Cisinski and Déglise11, Proposition 3.2.8, Corollary 3.3.5]).
$i$
(see [Reference Cisinski and Déglise11, Proposition 3.2.8, Corollary 3.3.5]).
If
![]() $p:V\rightarrow X$
is a vector bundle with 0-section
$p:V\rightarrow X$
is a vector bundle with 0-section
![]() $s:X\rightarrow V$
, we have the endomorphism
$s:X\rightarrow V$
, we have the endomorphism
![]() $\unicode[STIX]{x1D6F4}^{V}:\operatorname{SH}(X)\rightarrow \operatorname{SH}(X)$
defined as
$\unicode[STIX]{x1D6F4}^{V}:\operatorname{SH}(X)\rightarrow \operatorname{SH}(X)$
defined as
![]() $\unicode[STIX]{x1D6F4}^{V}:=p_{\#}s_{\ast }$
. This is an auto-equivalence, with quasi-inverse
$\unicode[STIX]{x1D6F4}^{V}:=p_{\#}s_{\ast }$
. This is an auto-equivalence, with quasi-inverse
![]() $\unicode[STIX]{x1D6F4}^{-V}:=s^{!}p^{\ast }$
. For
$\unicode[STIX]{x1D6F4}^{-V}:=s^{!}p^{\ast }$
. For
![]() $f:X\rightarrow Y$
smooth, there are canonical isomorphisms
$f:X\rightarrow Y$
smooth, there are canonical isomorphisms
where
![]() $T_{f}$
is the relative tangent bundle of
$T_{f}$
is the relative tangent bundle of
![]() $f$
.
$f$
.
For
![]() $\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
$\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
![]() $\mathbf{Sm}/X$
, we let
$\mathbf{Sm}/X$
, we let
![]() $Y/X\in \operatorname{SH}(X)$
denote the object
$Y/X\in \operatorname{SH}(X)$
denote the object
![]() $\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})$
and for
$\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})$
and for
![]() $\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
$\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
![]() $\mathbf{Sch}/X$
, we let
$\mathbf{Sch}/X$
, we let
![]() $Y_{\operatorname{B-M}}/X\in \operatorname{SH}(X)$
denote the object
$Y_{\operatorname{B-M}}/X\in \operatorname{SH}(X)$
denote the object
![]() $\unicode[STIX]{x1D70B}_{Y!}(1_{Y})$
. Sending
$\unicode[STIX]{x1D70B}_{Y!}(1_{Y})$
. Sending
![]() $Y\in \mathbf{Sm}/X$
to
$Y\in \mathbf{Sm}/X$
to
![]() $Y/X$
defines a functor
$Y/X$
defines a functor
and sending
![]() $Y\in \mathbf{Sch}/X$
to
$Y\in \mathbf{Sch}/X$
to
![]() $Y_{\operatorname{B-M}}/X$
defines a functor
$Y_{\operatorname{B-M}}/X$
defines a functor
where
![]() $\mathbf{Sch}^{\text{pr}}/X$
is the subcategory of proper morphisms in
$\mathbf{Sch}^{\text{pr}}/X$
is the subcategory of proper morphisms in
![]() $\mathbf{Sch}/X$
. For a morphism
$\mathbf{Sch}/X$
. For a morphism
![]() $g:Y\rightarrow Z$
in
$g:Y\rightarrow Z$
in
![]() $\mathbf{Sm}/X$
, the map
$\mathbf{Sm}/X$
, the map
![]() $g/X:Y/X\rightarrow Z/X$
is induced by the counit of the adjunction
$g/X:Y/X\rightarrow Z/X$
is induced by the counit of the adjunction
![]() $e_{g}:g_{!}g^{!}\rightarrow \text{Id}_{\operatorname{SH}(Z)}$
as the composition
$e_{g}:g_{!}g^{!}\rightarrow \text{Id}_{\operatorname{SH}(Z)}$
as the composition
For a proper morphism
![]() $g:Z\rightarrow Y$
in
$g:Z\rightarrow Y$
in
![]() $\mathbf{Sch}/X$
the map
$\mathbf{Sch}/X$
the map
![]() $g/X_{\operatorname{B-M}}:Y/X_{\operatorname{B-M}}\rightarrow Z/X_{\operatorname{B-M}}$
is the composition
$g/X_{\operatorname{B-M}}:Y/X_{\operatorname{B-M}}\rightarrow Z/X_{\operatorname{B-M}}$
is the composition
where
![]() $u_{g}:\text{Id}_{\operatorname{SH}(Y)}\rightarrow g_{\ast }g^{\ast }$
is the unit of the adjunction.
$u_{g}:\text{Id}_{\operatorname{SH}(Y)}\rightarrow g_{\ast }g^{\ast }$
is the unit of the adjunction.
Remark 1.1. Using the construction of
![]() $\operatorname{SH}(X)$
as the homotopy category of the category of symmetric
$\operatorname{SH}(X)$
as the homotopy category of the category of symmetric
![]() $T$
-spectra with respect to the
$T$
-spectra with respect to the
![]() $T$
-stable
$T$
-stable
![]() $\mathbb{A}^{1}$
-Nisnevich model structure [Reference Jardine20], the object
$\mathbb{A}^{1}$
-Nisnevich model structure [Reference Jardine20], the object
![]() $Y/X$
is canonically isomorphic to the usual
$Y/X$
is canonically isomorphic to the usual
![]() $T$
-suspension spectrum
$T$
-suspension spectrum
![]() $\unicode[STIX]{x1D6F4}_{T}^{\infty }Y_{+}$
and for
$\unicode[STIX]{x1D6F4}_{T}^{\infty }Y_{+}$
and for
![]() $g:Y\rightarrow Z$
a morphism in
$g:Y\rightarrow Z$
a morphism in
![]() $\mathbf{Sm}/X$
, the map
$\mathbf{Sm}/X$
, the map
![]() $g/X:Y/X\rightarrow Z/X$
is the map
$g/X:Y/X\rightarrow Z/X$
is the map
![]() $\unicode[STIX]{x1D6F4}_{T}^{\infty }g_{+}:\unicode[STIX]{x1D6F4}_{T}^{\infty }Y_{+}\rightarrow \unicode[STIX]{x1D6F4}_{T}^{\infty }Z_{+}$
. We mention this only to orient the reader; we will not be needing this fact in our discussion.
$\unicode[STIX]{x1D6F4}_{T}^{\infty }g_{+}:\unicode[STIX]{x1D6F4}_{T}^{\infty }Y_{+}\rightarrow \unicode[STIX]{x1D6F4}_{T}^{\infty }Z_{+}$
. We mention this only to orient the reader; we will not be needing this fact in our discussion.
For
![]() $\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
$\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
in
![]() $\mathbf{Sm}/X$
, there is a morphism
$\mathbf{Sm}/X$
, there is a morphism
defined as follows: we consider
![]() $Y\times _{X}Y$
as a
$Y\times _{X}Y$
as a
![]() $Y$
-scheme via
$Y$
-scheme via
![]() $p_{2}$
. We have the canonical isomorphisms
$p_{2}$
. We have the canonical isomorphisms
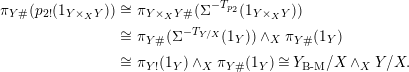 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{Y\#}(p_{2!}(1_{Y\times _{X}Y})) & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y\times _{X}Y\#}(\unicode[STIX]{x1D6F4}^{-T_{p_{2}}}(1_{Y\times _{X}Y}))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y\#}(\unicode[STIX]{x1D6F4}^{-T_{Y/X}}(1_{Y}))\wedge _{X}\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y!}(1_{Y})\wedge _{X}\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})\cong Y_{\operatorname{B-M}}/X\wedge _{X}Y/X.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{Y\#}(p_{2!}(1_{Y\times _{X}Y})) & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y\times _{X}Y\#}(\unicode[STIX]{x1D6F4}^{-T_{p_{2}}}(1_{Y\times _{X}Y}))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y\#}(\unicode[STIX]{x1D6F4}^{-T_{Y/X}}(1_{Y}))\wedge _{X}\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{Y!}(1_{Y})\wedge _{X}\unicode[STIX]{x1D70B}_{Y\#}(1_{Y})\cong Y_{\operatorname{B-M}}/X\wedge _{X}Y/X.\nonumber\end{eqnarray}$$
The diagonal section
![]() $s_{\unicode[STIX]{x1D6FF}}:Y\rightarrow Y\times _{X}Y$
to
$s_{\unicode[STIX]{x1D6FF}}:Y\rightarrow Y\times _{X}Y$
to
![]() $p_{2}$
is a proper morphism in
$p_{2}$
is a proper morphism in
![]() $\mathbf{Sch}/Y$
, giving the map
$\mathbf{Sch}/Y$
, giving the map
in
![]() $\operatorname{SH}(Y)$
. Applying
$\operatorname{SH}(Y)$
. Applying
![]() $\unicode[STIX]{x1D70B}_{Y\#}$
and using the above-mentioned isomorphism gives the map
$\unicode[STIX]{x1D70B}_{Y\#}$
and using the above-mentioned isomorphism gives the map
The map
![]() $ev_{Y}$
is then defined as the composition
$ev_{Y}$
is then defined as the composition
For
![]() $\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
a proper morphism in
$\unicode[STIX]{x1D70B}_{Y}:Y\rightarrow X$
a proper morphism in
![]() $\mathbf{Sch}/X$
, we have the map
$\mathbf{Sch}/X$
, we have the map
If
![]() $Y$
is smooth over
$Y$
is smooth over
![]() $X$
, we consider
$X$
, we consider
![]() $Y\times _{X}Y$
as a smooth
$Y\times _{X}Y$
as a smooth
![]() $Y$
-scheme via
$Y$
-scheme via
![]() $p_{1}$
, giving the map
$p_{1}$
, giving the map
Applying
![]() $\unicode[STIX]{x1D70B}_{Y!}$
and using the canonical isomorphism
$\unicode[STIX]{x1D70B}_{Y!}$
and using the canonical isomorphism
constructed as above gives the map
For
![]() $Y$
smooth and proper over
$Y$
smooth and proper over
![]() $X$
, define the map
$X$
, define the map
![]() $\unicode[STIX]{x1D6FF}_{Y}:1_{X}\rightarrow Y/X\wedge _{X}Y_{\operatorname{B-M}}/X$
as the composition
$\unicode[STIX]{x1D6FF}_{Y}:1_{X}\rightarrow Y/X\wedge _{X}Y_{\operatorname{B-M}}/X$
as the composition
Recall that an object
![]() $x\in \operatorname{SH}(X)$
has the dual
$x\in \operatorname{SH}(X)$
has the dual
![]() $x^{\vee }:={\mathcal{H}}om_{X}(x,1_{X})$
, giving the evaluation map
$x^{\vee }:={\mathcal{H}}om_{X}(x,1_{X})$
, giving the evaluation map
adjoint to the identity on
![]() $x^{\vee }$
. The map
$x^{\vee }$
. The map
![]() $ev$
in turn induces maps
$ev$
in turn induces maps
![]() $can_{a}:x^{\vee }\wedge _{X}a\rightarrow {\mathcal{H}}om_{X}(x,a)$
and
$can_{a}:x^{\vee }\wedge _{X}a\rightarrow {\mathcal{H}}om_{X}(x,a)$
and
![]() $can_{a}^{\prime }:a\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x^{\vee },a)$
;
$can_{a}^{\prime }:a\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x^{\vee },a)$
;
![]() $x$
is called strongly dualizable if the morphism
$x$
is called strongly dualizable if the morphism
![]() $can_{x}:x^{\vee }\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x,x)$
is an isomorphism. This is equivalent to the existence of an object
$can_{x}:x^{\vee }\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x,x)$
is an isomorphism. This is equivalent to the existence of an object
![]() $y\in \operatorname{SH}(X)$
and morphisms
$y\in \operatorname{SH}(X)$
and morphisms
![]() $\unicode[STIX]{x1D6FF}_{x}:1_{X}\rightarrow x\wedge _{X}y$
,
$\unicode[STIX]{x1D6FF}_{x}:1_{X}\rightarrow x\wedge _{X}y$
,
![]() $ev_{x}:y\wedge _{X}x\rightarrow 1_{X}$
, such that
$ev_{x}:y\wedge _{X}x\rightarrow 1_{X}$
, such that
(see [Reference May28, Theorem 2.6]). In this case, there is a canonical isomorphism
![]() $y\cong x^{\vee }$
with
$y\cong x^{\vee }$
with
![]() $ev_{x}$
going over to
$ev_{x}$
going over to
![]() $ev$
, and
$ev$
, and
![]() $\unicode[STIX]{x1D6FF}_{x}$
going over to the map
$\unicode[STIX]{x1D6FF}_{x}$
going over to the map
given as the image of
![]() $\text{Id}_{x}$
under the sequence of isomorphisms
$\text{Id}_{x}$
under the sequence of isomorphisms
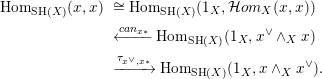 $$\begin{eqnarray}\displaystyle \text{Hom}_{\operatorname{SH}(X)}(x,x) & & \displaystyle \cong \text{Hom}_{\operatorname{SH}(X)}(1_{X},{\mathcal{H}}om_{X}(x,x))\nonumber\\ \displaystyle & & \displaystyle \xleftarrow[{}]{can_{x\ast }}\text{Hom}_{\operatorname{SH}(X)}(1_{X},x^{\vee }\wedge _{X}x)\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D70F}_{x^{\vee },x\ast }}\text{Hom}_{\operatorname{SH}(X)}(1_{X},x\wedge _{X}x^{\vee }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{\operatorname{SH}(X)}(x,x) & & \displaystyle \cong \text{Hom}_{\operatorname{SH}(X)}(1_{X},{\mathcal{H}}om_{X}(x,x))\nonumber\\ \displaystyle & & \displaystyle \xleftarrow[{}]{can_{x\ast }}\text{Hom}_{\operatorname{SH}(X)}(1_{X},x^{\vee }\wedge _{X}x)\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D70F}_{x^{\vee },x\ast }}\text{Hom}_{\operatorname{SH}(X)}(1_{X},x\wedge _{X}x^{\vee }).\nonumber\end{eqnarray}$$
Proposition 1.2.
(1) For
 $f:Y\rightarrow X$
smooth and proper, the triple
$f:Y\rightarrow X$
smooth and proper, the triple
 $(Y_{\operatorname{B-M}}/X,\unicode[STIX]{x1D6FF}_{Y},ev_{Y})$
exhibits
$(Y_{\operatorname{B-M}}/X,\unicode[STIX]{x1D6FF}_{Y},ev_{Y})$
exhibits
 $Y/X$
as a strongly dualizable object of
$Y/X$
as a strongly dualizable object of
 $\operatorname{SH}(X)$
with dual
$\operatorname{SH}(X)$
with dual
 $Y_{\operatorname{B-M}}/X$
.
$Y_{\operatorname{B-M}}/X$
.(2) Let
 $\{j_{i}:U_{i}\rightarrow X,i=1,\ldots ,n\}$
be a finite Nisnevich open cover of
$\{j_{i}:U_{i}\rightarrow X,i=1,\ldots ,n\}$
be a finite Nisnevich open cover of
 $X$
. Suppose that for
$X$
. Suppose that for
 $x\in \operatorname{SH}(X)$
,
$x\in \operatorname{SH}(X)$
,
 $j_{i}^{\ast }x\in \operatorname{SH}(U_{i})$
is strongly dualizable for all
$j_{i}^{\ast }x\in \operatorname{SH}(U_{i})$
is strongly dualizable for all
 $i$
. Then
$i$
. Then
 $x$
is a strongly dualizable object of
$x$
is a strongly dualizable object of
 $\operatorname{SH}(X)$
.
$\operatorname{SH}(X)$
.(3) The class of strongly dualizable objects in
 $\operatorname{SH}(X)$
is closed under
$\operatorname{SH}(X)$
is closed under
 $\wedge _{X}$
and
$\wedge _{X}$
and  $$\begin{eqnarray}(x_{1}\wedge _{X}x_{2})^{\vee }\cong x_{1}^{\vee }\wedge _{X}x_{2}^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}(x_{1}\wedge _{X}x_{2})^{\vee }\cong x_{1}^{\vee }\wedge _{X}x_{2}^{\vee }.\end{eqnarray}$$
(4) If
 $f:X\rightarrow Y$
is a morphism in
$f:X\rightarrow Y$
is a morphism in
 $\mathbf{Sch}/S$
and
$\mathbf{Sch}/S$
and
 $y\in \operatorname{SH}(Y)$
is strongly dualizable, then
$y\in \operatorname{SH}(Y)$
is strongly dualizable, then
 $f^{\ast }y$
is strongly dualizable with dual
$f^{\ast }y$
is strongly dualizable with dual
 $f^{\ast }(y^{\vee })$
.
$f^{\ast }(y^{\vee })$
.(5) The class of strongly dualizable objects in
 $\operatorname{SH}(X)$
satisfies the 2 out of 3 property with respect to distinguished triangles: if
$\operatorname{SH}(X)$
satisfies the 2 out of 3 property with respect to distinguished triangles: if
 $x_{1}\xrightarrow[{}]{u}x_{2}\xrightarrow[{}]{v}x_{3}\xrightarrow[{}]{w}x_{1}[1]$
is a distinguished triangle in
$x_{1}\xrightarrow[{}]{u}x_{2}\xrightarrow[{}]{v}x_{3}\xrightarrow[{}]{w}x_{1}[1]$
is a distinguished triangle in
 $\operatorname{SH}(X)$
and two of the
$\operatorname{SH}(X)$
and two of the
 $x_{i}$
are strongly dualizable, then so is the third. Moreover, the triangle is distinguished.
$x_{i}$
are strongly dualizable, then so is the third. Moreover, the triangle is distinguished. $$\begin{eqnarray}x_{3}^{\vee }\xrightarrow[{}]{v^{\vee }}x_{2}^{\vee }\xrightarrow[{}]{u^{\vee }}x_{1}^{\vee }\xrightarrow[{}]{-w^{\vee }[1]}x_{3}[1]\end{eqnarray}$$
$$\begin{eqnarray}x_{3}^{\vee }\xrightarrow[{}]{v^{\vee }}x_{2}^{\vee }\xrightarrow[{}]{u^{\vee }}x_{1}^{\vee }\xrightarrow[{}]{-w^{\vee }[1]}x_{3}[1]\end{eqnarray}$$
Proof. (1) follows from [Reference Cisinski and Déglise11, Theorem 2.4.50, Proposition 2.4.31]. For (2), take
![]() $a\in \operatorname{SH}(X)$
and consider the map
$a\in \operatorname{SH}(X)$
and consider the map
![]() $can_{x}:x^{\vee }\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x,x)$
. Then
$can_{x}:x^{\vee }\wedge _{X}x\rightarrow {\mathcal{H}}om_{X}(x,x)$
. Then
![]() $j_{i}^{\ast }can$
is the canonical map
$j_{i}^{\ast }can$
is the canonical map
![]() $:j_{i}^{\ast }x^{\vee }\wedge _{U_{i}}j_{i}^{\ast }x\rightarrow {\mathcal{H}}om_{U_{i}}(j_{i}^{\ast }x,j_{i}^{\ast }x)$
, after making the evident identifications. Thus
$:j_{i}^{\ast }x^{\vee }\wedge _{U_{i}}j_{i}^{\ast }x\rightarrow {\mathcal{H}}om_{U_{i}}(j_{i}^{\ast }x,j_{i}^{\ast }x)$
, after making the evident identifications. Thus
![]() $j_{i}^{\ast }can$
is an isomorphism for all
$j_{i}^{\ast }can$
is an isomorphism for all
![]() $i$
and
$i$
and
![]() $can$
is then an isomorphism by the weak Nisnevich descent property. (3) follows from the characterization of strongly dualizable objects via the existence of the maps
$can$
is then an isomorphism by the weak Nisnevich descent property. (3) follows from the characterization of strongly dualizable objects via the existence of the maps
![]() $\unicode[STIX]{x1D6FF},ev$
satisfying the identities (1.1); (4) is similar, noting that
$\unicode[STIX]{x1D6FF},ev$
satisfying the identities (1.1); (4) is similar, noting that
![]() $f^{\ast }$
is a symmetric monoidal functor. The assertion (5) is proven by May [Reference May27, Theorem 0.1] for a symmetric monoidal triangulated category subject to certain axioms, which are satisfied by
$f^{\ast }$
is a symmetric monoidal functor. The assertion (5) is proven by May [Reference May27, Theorem 0.1] for a symmetric monoidal triangulated category subject to certain axioms, which are satisfied by
![]() $\operatorname{SH}(X)$
.
$\operatorname{SH}(X)$
.
Definition 1.3. Let
![]() $x\in \operatorname{SH}(X)$
be a strongly dualizable object. The Euler characteristic
$x\in \operatorname{SH}(X)$
be a strongly dualizable object. The Euler characteristic
![]() $\unicode[STIX]{x1D712}(x/X)\in \text{End}_{\operatorname{SH}(X)}(1_{X})$
is the composition
$\unicode[STIX]{x1D712}(x/X)\in \text{End}_{\operatorname{SH}(X)}(1_{X})$
is the composition
Remark 1.4. If
![]() $X=\text{Spec }F$
for
$X=\text{Spec }F$
for
![]() $F$
a perfect field, then Morel’s theorem [Reference Morel30, Theorem 6.4.1] identifies
$F$
a perfect field, then Morel’s theorem [Reference Morel30, Theorem 6.4.1] identifies
![]() $\text{End}_{\operatorname{SH}(X)}(1_{X})$
with the Grothendieck–Witt group
$\text{End}_{\operatorname{SH}(X)}(1_{X})$
with the Grothendieck–Witt group
![]() $\operatorname{GW}(F)$
.
$\operatorname{GW}(F)$
.
Definition 1.5. 1. Let
![]() $f:E\rightarrow B$
be in
$f:E\rightarrow B$
be in
![]() $\mathbf{Sm}/B$
with
$\mathbf{Sm}/B$
with
![]() $E/B$
a strongly dualizable object in
$E/B$
a strongly dualizable object in
![]() $\operatorname{SH}(B)$
. The relative transfer
$\operatorname{SH}(B)$
. The relative transfer
![]() $\text{Tr}_{f/B}:1_{B}\rightarrow E/B$
is defined as follows: consider the diagonal morphism
$\text{Tr}_{f/B}:1_{B}\rightarrow E/B$
is defined as follows: consider the diagonal morphism
Applying
![]() $f_{\#}$
gives the morphism
$f_{\#}$
gives the morphism
By duality, we have the isomorphism
defined by sending a morphism
![]() $g:E/B\rightarrow E/B\wedge _{B}E/B$
to the composition
$g:E/B\rightarrow E/B\wedge _{B}E/B$
to the composition
We set
2. Suppose we have
![]() $f:E\rightarrow B$
in
$f:E\rightarrow B$
in
![]() $\mathbf{Sm}/B$
as in (1), with
$\mathbf{Sm}/B$
as in (1), with
![]() $\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
in
$\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
in
![]() $\mathbf{Sm}/S$
, giving the structure morphism
$\mathbf{Sm}/S$
, giving the structure morphism
![]() $\unicode[STIX]{x1D70B}_{E}:E\rightarrow S$
,
$\unicode[STIX]{x1D70B}_{E}:E\rightarrow S$
,
![]() $\unicode[STIX]{x1D70B}_{E}:=\unicode[STIX]{x1D70B}_{B}\circ f$
. Define the transfer
$\unicode[STIX]{x1D70B}_{E}:=\unicode[STIX]{x1D70B}_{B}\circ f$
. Define the transfer
![]() $\text{Tr}(f/S):B/S\rightarrow E/S$
by
$\text{Tr}(f/S):B/S\rightarrow E/S$
by
where we use the canonical isomorphism
Lemma 1.6. Given
![]() $f:E\rightarrow B$
as in Definition 1.5(1), let
$f:E\rightarrow B$
as in Definition 1.5(1), let
![]() $g:B^{\prime }\rightarrow B$
be a morphism in
$g:B^{\prime }\rightarrow B$
be a morphism in
![]() $\mathbf{Sch}/S$
and let
$\mathbf{Sch}/S$
and let
![]() $f^{\prime }:E^{\prime }\rightarrow B^{\prime }$
be the pullback
$f^{\prime }:E^{\prime }\rightarrow B^{\prime }$
be the pullback
![]() $E^{\prime }:=E\times _{B}B^{\prime }$
,
$E^{\prime }:=E\times _{B}B^{\prime }$
,
![]() $f^{\prime }=p_{2}$
. Then
$f^{\prime }=p_{2}$
. Then
![]() $f^{\prime }:E^{\prime }\rightarrow B^{\prime }$
is strongly dualizable in
$f^{\prime }:E^{\prime }\rightarrow B^{\prime }$
is strongly dualizable in
![]() $\operatorname{SH}(B^{\prime })$
, there are canonical isomorphisms
$\operatorname{SH}(B^{\prime })$
, there are canonical isomorphisms
![]() $E^{\prime }/B^{\prime }\cong g^{\ast }(E/B)$
,
$E^{\prime }/B^{\prime }\cong g^{\ast }(E/B)$
,
![]() $1_{B^{\prime }}\cong g^{\ast }(1_{B})$
and via these isomorphisms, we have
$1_{B^{\prime }}\cong g^{\ast }(1_{B})$
and via these isomorphisms, we have
Moreover, if
![]() $\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
is in
$\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
is in
![]() $\mathbf{Sm}/S$
, if
$\mathbf{Sm}/S$
, if
![]() $g_{0}:S^{\prime }\rightarrow S$
is a morphism in
$g_{0}:S^{\prime }\rightarrow S$
is a morphism in
![]() $\mathbf{Sch}/S$
, if
$\mathbf{Sch}/S$
, if
![]() $B^{\prime }=S^{\prime }\times _{S}B$
and
$B^{\prime }=S^{\prime }\times _{S}B$
and
![]() $g:B^{\prime }\rightarrow B$
is the projection, then there is a canonical isomorphism
$g:B^{\prime }\rightarrow B$
is the projection, then there is a canonical isomorphism
![]() $B^{\prime }/S^{\prime }\cong g_{0}^{\ast }(B/S)$
and via this isomorphism
$B^{\prime }/S^{\prime }\cong g_{0}^{\ast }(B/S)$
and via this isomorphism
Proof. For the first assertion, we have the exchange isomorphism (see [Reference Cisinski and Déglise11, § 1.1.6] or [Reference Ayoub5, § 1.4.5])
associated to the Cartesian diagram

which gives the isomorphism
We have the canonical isomorphism
![]() $1_{B^{\prime }}\cong g^{\ast }(1_{B})$
as well. Since
$1_{B^{\prime }}\cong g^{\ast }(1_{B})$
as well. Since
![]() $g^{\ast }$
is a symmetric monoidal functor, the assumption that
$g^{\ast }$
is a symmetric monoidal functor, the assumption that
![]() $E/B$
is strongly dualizable in
$E/B$
is strongly dualizable in
![]() $\operatorname{SH}(B)$
implies that
$\operatorname{SH}(B)$
implies that
![]() $E^{\prime }/B^{\prime }$
is strongly dualizable in
$E^{\prime }/B^{\prime }$
is strongly dualizable in
![]() $\operatorname{SH}(B^{\prime })$
with
$\operatorname{SH}(B^{\prime })$
with
![]() ${E^{\prime }/B^{\prime }}^{\vee }$
canonically isomorphic to
${E^{\prime }/B^{\prime }}^{\vee }$
canonically isomorphic to
![]() $g^{\ast }(E/B^{\vee })$
. Moreover, via these isomorphisms, we have
$g^{\ast }(E/B^{\vee })$
. Moreover, via these isomorphisms, we have
Finally, since the exchange isomorphism is a natural transformation, we have
and thus
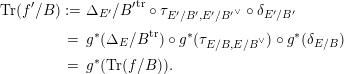 $$\begin{eqnarray}\displaystyle \text{Tr}(f^{\prime }/B) & := & \displaystyle {\unicode[STIX]{x1D6E5}_{E^{\prime }}/B^{\prime }}^{\text{tr}}\circ \unicode[STIX]{x1D70F}_{E^{\prime }/B^{\prime },{E^{\prime }/B^{\prime }}^{\vee }}\circ \unicode[STIX]{x1D6FF}_{E^{\prime }/B^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }({\unicode[STIX]{x1D6E5}_{E}/B}^{\text{tr}})\circ g^{\ast }(\unicode[STIX]{x1D70F}_{E/B,E/B^{\vee }})\circ g^{\ast }(\unicode[STIX]{x1D6FF}_{E/B})\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }(\text{Tr}(f/B)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Tr}(f^{\prime }/B) & := & \displaystyle {\unicode[STIX]{x1D6E5}_{E^{\prime }}/B^{\prime }}^{\text{tr}}\circ \unicode[STIX]{x1D70F}_{E^{\prime }/B^{\prime },{E^{\prime }/B^{\prime }}^{\vee }}\circ \unicode[STIX]{x1D6FF}_{E^{\prime }/B^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }({\unicode[STIX]{x1D6E5}_{E}/B}^{\text{tr}})\circ g^{\ast }(\unicode[STIX]{x1D70F}_{E/B,E/B^{\vee }})\circ g^{\ast }(\unicode[STIX]{x1D6FF}_{E/B})\nonumber\\ \displaystyle & = & \displaystyle g^{\ast }(\text{Tr}(f/B)).\nonumber\end{eqnarray}$$
The proof that
![]() $\text{Tr}(f^{\prime }/S^{\prime })=g_{0}^{\ast }(\text{Tr}(f/S))$
is similar and is left to the reader.
$\text{Tr}(f^{\prime }/S^{\prime })=g_{0}^{\ast }(\text{Tr}(f/S))$
is similar and is left to the reader.
Lemma 1.7. Let
![]() $f:E\rightarrow B$
be in
$f:E\rightarrow B$
be in
![]() $\mathbf{Sm}/B$
, with
$\mathbf{Sm}/B$
, with
![]() $E/B$
strongly dualizable in
$E/B$
strongly dualizable in
![]() $\operatorname{SH}(B)$
. Then
$\operatorname{SH}(B)$
. Then
is equal to
![]() $\unicode[STIX]{x1D712}(E/B)$
.
$\unicode[STIX]{x1D712}(E/B)$
.
Proof.
![]() $f/B\circ \text{Tr}(f/B)$
is the composition
$f/B\circ \text{Tr}(f/B)$
is the composition
The map
![]() $\unicode[STIX]{x1D6E5}_{E}/B^{\text{tr}}$
is the composition
$\unicode[STIX]{x1D6E5}_{E}/B^{\text{tr}}$
is the composition
 $$\begin{eqnarray}\displaystyle E/B^{\vee }\wedge _{B}E/B\xrightarrow[{}]{\text{Id}\wedge \unicode[STIX]{x1D6E5}_{E}/B}E/B^{\vee }\wedge _{B}E/B\wedge _{B}E/B & & \displaystyle \nonumber\\ \displaystyle \xrightarrow[{}]{ev_{E/B}\wedge \text{Id}}1_{B}\wedge _{B}E/B\cong E/B. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E/B^{\vee }\wedge _{B}E/B\xrightarrow[{}]{\text{Id}\wedge \unicode[STIX]{x1D6E5}_{E}/B}E/B^{\vee }\wedge _{B}E/B\wedge _{B}E/B & & \displaystyle \nonumber\\ \displaystyle \xrightarrow[{}]{ev_{E/B}\wedge \text{Id}}1_{B}\wedge _{B}E/B\cong E/B. & & \displaystyle \nonumber\end{eqnarray}$$
We have the commutative diagram

Thus
Remark 1.8. Hoyois [Reference Hoyois18, Remark 3.5] has defined the relative transfer for a smooth proper map
![]() $f:E\rightarrow B$
using the six-functor formalism, and has noted the identity
$f:E\rightarrow B$
using the six-functor formalism, and has noted the identity
![]() $f/B\circ \text{Tr}(f/B)=\unicode[STIX]{x1D712}(E/B)$
in this case.
$f/B\circ \text{Tr}(f/B)=\unicode[STIX]{x1D712}(E/B)$
in this case.
Lemma 1.9. Suppose
![]() $\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
is in
$\unicode[STIX]{x1D70B}_{B}:B\rightarrow S$
is in
![]() $\mathbf{Sm}/S$
, and
$\mathbf{Sm}/S$
, and
![]() $E=F\times _{S}B$
for some
$E=F\times _{S}B$
for some
![]() $\unicode[STIX]{x1D70B}_{F}:F\rightarrow S$
in
$\unicode[STIX]{x1D70B}_{F}:F\rightarrow S$
in
![]() $\mathbf{Sm}/S$
, with
$\mathbf{Sm}/S$
, with
![]() $f:E\rightarrow B$
the projection. Suppose that
$f:E\rightarrow B$
the projection. Suppose that
![]() $F/S$
is strongly dualizable. Then
$F/S$
is strongly dualizable. Then
![]() $E/B$
is strongly dualizable and
$E/B$
is strongly dualizable and
![]() $f/S\circ \text{Tr}(f/S)$
is multiplication by
$f/S\circ \text{Tr}(f/S)$
is multiplication by
![]() $\unicode[STIX]{x1D712}(F/S)$
.
$\unicode[STIX]{x1D712}(F/S)$
.
Proof. Under our assumptions, we have
![]() $E/B=\unicode[STIX]{x1D70B}_{B}^{\ast }(F/S)$
. Since
$E/B=\unicode[STIX]{x1D70B}_{B}^{\ast }(F/S)$
. Since
![]() $\unicode[STIX]{x1D70B}_{B}^{\ast }$
is a symmetric monoidal functor, it follows that
$\unicode[STIX]{x1D70B}_{B}^{\ast }$
is a symmetric monoidal functor, it follows that
![]() $E/B^{\vee }=\unicode[STIX]{x1D70B}_{B}^{\ast }(F/S^{\vee })$
and
$E/B^{\vee }=\unicode[STIX]{x1D70B}_{B}^{\ast }(F/S^{\vee })$
and
![]() $\text{Tr}(E/B)=\unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S))$
. Thus
$\text{Tr}(E/B)=\unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S))$
. Thus
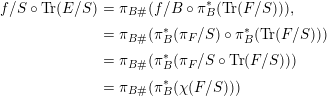 $$\begin{eqnarray}\displaystyle f/S\circ \text{Tr}(E/S) & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(f/B\circ \unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S))),\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D70B}_{F}/S)\circ \unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S)))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D70B}_{F}/S\circ \text{Tr}(F/S)))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D712}(F/S)))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f/S\circ \text{Tr}(E/S) & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(f/B\circ \unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S))),\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D70B}_{F}/S)\circ \unicode[STIX]{x1D70B}_{B}^{\ast }(\text{Tr}(F/S)))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D70B}_{F}/S\circ \text{Tr}(F/S)))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{B\#}(\unicode[STIX]{x1D70B}_{B}^{\ast }(\unicode[STIX]{x1D712}(F/S)))\nonumber\end{eqnarray}$$
which is multiplication by
![]() $\unicode[STIX]{x1D712}(F/S)$
.
$\unicode[STIX]{x1D712}(F/S)$
.
Let
![]() $f:E\rightarrow B$
be a finite type morphism, with
$f:E\rightarrow B$
be a finite type morphism, with
![]() $B\in \mathbf{Sch}/S$
and let
$B\in \mathbf{Sch}/S$
and let
![]() $F$
be in
$F$
be in
![]() $\mathbf{Sch}/S$
. We say that
$\mathbf{Sch}/S$
. We say that
![]() $f$
is a Nisnevich locally trivial bundle with fiber
$f$
is a Nisnevich locally trivial bundle with fiber
![]() $F$
if there is a covering family
$F$
if there is a covering family
![]() $\{g_{i}:U_{i}\rightarrow B,i\in I\}$
for the Nisnevich topology on
$\{g_{i}:U_{i}\rightarrow B,i\in I\}$
for the Nisnevich topology on
![]() $B$
and isomorphisms of
$B$
and isomorphisms of
![]() $U_{i}$
-schemes
$U_{i}$
-schemes
![]() $E\times _{B}U_{i}\cong F\times _{S}U_{i}$
for each
$E\times _{B}U_{i}\cong F\times _{S}U_{i}$
for each
![]() $i\in I$
.
$i\in I$
.
Theorem 1.10. Let
![]() $F$
and
$F$
and
![]() $B$
be in
$B$
be in
![]() $\mathbf{Sm}/S$
and let
$\mathbf{Sm}/S$
and let
![]() $f:E\rightarrow B$
in
$f:E\rightarrow B$
in
![]() $\mathbf{Sm}/B$
be a Nisnevich locally trivial bundle with fiber
$\mathbf{Sm}/B$
be a Nisnevich locally trivial bundle with fiber
![]() $F$
.
$F$
.
1. If
![]() $F/S$
is strongly dualizable in
$F/S$
is strongly dualizable in
![]() $\operatorname{SH}(S)$
, then
$\operatorname{SH}(S)$
, then
![]() $E/B$
is strongly dualizable in
$E/B$
is strongly dualizable in
![]() $\operatorname{SH}(B)$
.
$\operatorname{SH}(B)$
.
2. Suppose that
![]() $F/S$
is strongly dualizable in
$F/S$
is strongly dualizable in
![]() $\operatorname{SH}(S)$
. Let
$\operatorname{SH}(S)$
. Let
![]() ${\mathcal{E}}\in \operatorname{SH}(S)$
be a motivic ring spectrum such that the map
${\mathcal{E}}\in \operatorname{SH}(S)$
be a motivic ring spectrum such that the map
![]() $\unicode[STIX]{x1D712}(F/S):1_{S}\rightarrow 1_{S}$
induces an isomorphism on
$\unicode[STIX]{x1D712}(F/S):1_{S}\rightarrow 1_{S}$
induces an isomorphism on
![]() ${\mathcal{E}}^{0,0}(S)$
. Then the map
${\mathcal{E}}^{0,0}(S)$
. Then the map
is split injective.
Proof. The assertion (1) follows from the isomorphism
![]() $g_{i}^{\ast }(E/B)\cong F\times _{S}U_{i}/U_{i}$
, and Proposition 1.2(2, 4).
$g_{i}^{\ast }(E/B)\cong F\times _{S}U_{i}/U_{i}$
, and Proposition 1.2(2, 4).
For (2), we have
similarly
![]() ${\mathcal{E}}^{a,b}(B/S)=\unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(1_{B})$
and via these isomorphisms, the map
${\mathcal{E}}^{a,b}(B/S)=\unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(1_{B})$
and via these isomorphisms, the map
![]() $f/S^{\ast }:{\mathcal{E}}^{a,b}(B/S)\rightarrow {\mathcal{E}}^{a,b}(E/S)$
is the map
$f/S^{\ast }:{\mathcal{E}}^{a,b}(B/S)\rightarrow {\mathcal{E}}^{a,b}(E/S)$
is the map
![]() $f/B^{\ast }:\unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(1_{B})\rightarrow \unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(E/B)$
. We claim that the endomorphism
$f/B^{\ast }:\unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(1_{B})\rightarrow \unicode[STIX]{x1D70B}_{B}^{\ast }{\mathcal{E}}^{a,b}(E/B)$
. We claim that the endomorphism
is an isomorphism; assuming this the case, the map
![]() $\text{Tr}(E/B)^{\ast }$
gives a left quasi-inverse to
$\text{Tr}(E/B)^{\ast }$
gives a left quasi-inverse to
![]() $f/S^{\ast }$
.
$f/S^{\ast }$
.
By weak Nisnevich descent, it suffices to show that the pullback
is an isomorphism for all
![]() $i$
. But
$i$
. But
and
![]() $p_{U_{i}}\circ \text{Tr}(F\times _{S}U_{i}/U_{i})$
is multiplication by
$p_{U_{i}}\circ \text{Tr}(F\times _{S}U_{i}/U_{i})$
is multiplication by
![]() $\unicode[STIX]{x1D70B}_{U_{i}}^{\ast }\unicode[STIX]{x1D712}(F/S)$
. Using the multiplication
$\unicode[STIX]{x1D70B}_{U_{i}}^{\ast }\unicode[STIX]{x1D712}(F/S)$
. Using the multiplication
![]() $\unicode[STIX]{x1D707}$
in
$\unicode[STIX]{x1D707}$
in
![]() ${\mathcal{E}}$
, we have the commutative diagram
${\mathcal{E}}$
, we have the commutative diagram

and so
![]() $g_{i}^{\ast }(\text{Tr}(E/B)^{\ast }\circ f/B^{\ast })$
is an isomorphism by our assumption on
$g_{i}^{\ast }(\text{Tr}(E/B)^{\ast }\circ f/B^{\ast })$
is an isomorphism by our assumption on
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.
Remark 1.11. The above result is a motivic analog of the theorem of Becker–Gottlieb [Reference Becker and Gottlieb9, Theorem 5.7].
2 The case of split reductive groups: a conjecture
Let
![]() $G$
be a split reductive group scheme over a base scheme
$G$
be a split reductive group scheme over a base scheme
![]() $S$
, with Borel subgroup
$S$
, with Borel subgroup
![]() $B$
and maximal split torus
$B$
and maximal split torus
![]() $T\subset B$
. Let
$T\subset B$
. Let
![]() $N_{T}\supset T$
be the normalizer of
$N_{T}\supset T$
be the normalizer of
![]() $T$
in
$T$
in
![]() $G$
. We take the model
$G$
. We take the model
![]() $N_{T}\backslash EG$
for
$N_{T}\backslash EG$
for
![]() $BN_{T}$
(see the end of this section for details on our model for
$BN_{T}$
(see the end of this section for details on our model for
![]() $EG$
) and consider the
$EG$
) and consider the
![]() $N_{T}\backslash G$
-bundle
$N_{T}\backslash G$
-bundle
![]() $BN_{T}\rightarrow BG$
. For special
$BN_{T}\rightarrow BG$
. For special
![]() $G$
, that is, for
$G$
, that is, for
![]() $G=\operatorname{GL}_{n},\operatorname{SL}_{n},\operatorname{Sp}_{2n}$
,
$G=\operatorname{GL}_{n},\operatorname{SL}_{n},\operatorname{Sp}_{2n}$
,
![]() $BN_{T}\rightarrow BG$
is a Nisnevich locally trivial bundle, and so we can apply the motivic Becker–Gottlieb theorem developed in the previous section; for this, we need to compute the Euler characteristic
$BN_{T}\rightarrow BG$
is a Nisnevich locally trivial bundle, and so we can apply the motivic Becker–Gottlieb theorem developed in the previous section; for this, we need to compute the Euler characteristic
![]() $\unicode[STIX]{x1D712}(N_{T}\backslash G/S)$
.
$\unicode[STIX]{x1D712}(N_{T}\backslash G/S)$
.
Following a suggestion of Fabien Morel, who formulated the strong form, we have the following conjecture.
Conjecture 2.1.
Strong form: For
![]() $G$
a split reductive group scheme over a perfect field
$G$
a split reductive group scheme over a perfect field
![]() $k$
, we have
$k$
, we have
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash G)/k)=1$
in
$\unicode[STIX]{x1D712}((N_{T}\backslash G)/k)=1$
in
![]() $\operatorname{GW}(k)$
.
$\operatorname{GW}(k)$
.
Weak form: For
![]() $G$
a split reductive group scheme over a perfect field
$G$
a split reductive group scheme over a perfect field
![]() $k$
, the Euler characteristic
$k$
, the Euler characteristic
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash G)/k)$
is invertible in
$\unicode[STIX]{x1D712}((N_{T}\backslash G)/k)$
is invertible in
![]() $\operatorname{GW}(k)$
.
$\operatorname{GW}(k)$
.
The weak form suffices to apply the motivic Becker–Gottlieb transfer to the map
![]() $\unicode[STIX]{x1D70B}_{G}:BN_{T}(G)\rightarrow BG$
in case the
$\unicode[STIX]{x1D70B}_{G}:BN_{T}(G)\rightarrow BG$
in case the
![]() $N_{T}(G)\backslash G$
-bundle is Nisnevich locally trivial; see Theorem 2.5 below for a precise statement in case
$N_{T}(G)\backslash G$
-bundle is Nisnevich locally trivial; see Theorem 2.5 below for a precise statement in case
![]() $G=\operatorname{GL}_{n},\operatorname{SL}_{n}$
.
$G=\operatorname{GL}_{n},\operatorname{SL}_{n}$
.
For
![]() $S=\text{Spec }\mathbb{C}$
it is well-known that
$S=\text{Spec }\mathbb{C}$
it is well-known that
![]() $N_{T}(\mathbb{C})\backslash G(\mathbb{C})$
has (topological) Euler characteristic 1. This is also easy to prove:
$N_{T}(\mathbb{C})\backslash G(\mathbb{C})$
has (topological) Euler characteristic 1. This is also easy to prove:
![]() $T(\mathbb{C})\backslash G(\mathbb{C})$
is homotopy equivalent to
$T(\mathbb{C})\backslash G(\mathbb{C})$
is homotopy equivalent to
![]() $B(\mathbb{C})\backslash G(\mathbb{C})$
, which has homology the free abelian group on the closure of the Schubert cells
$B(\mathbb{C})\backslash G(\mathbb{C})$
, which has homology the free abelian group on the closure of the Schubert cells
![]() $B(\mathbb{C})wB(\mathbb{C})$
,
$B(\mathbb{C})wB(\mathbb{C})$
,
![]() $w\in W(G):=N_{T}(\mathbb{C})/T(\mathbb{C})$
; as these are all of even dimension, we have
$w\in W(G):=N_{T}(\mathbb{C})/T(\mathbb{C})$
; as these are all of even dimension, we have
![]() $\unicode[STIX]{x1D712}^{\text{top}}(G(\mathbb{C})/T(\mathbb{C}))=\#W(G)$
. As the covering space
$\unicode[STIX]{x1D712}^{\text{top}}(G(\mathbb{C})/T(\mathbb{C}))=\#W(G)$
. As the covering space
![]() $T(\mathbb{C})\backslash G(\mathbb{C})\rightarrow N_{T}(\mathbb{C})\backslash G(\mathbb{C})$
has degree
$T(\mathbb{C})\backslash G(\mathbb{C})\rightarrow N_{T}(\mathbb{C})\backslash G(\mathbb{C})$
has degree
![]() $\#W(G)$
, it follows that
$\#W(G)$
, it follows that
![]() $\unicode[STIX]{x1D712}^{\text{top}}(N_{T}(\mathbb{C})\backslash G(\mathbb{C}))=1$
.
$\unicode[STIX]{x1D712}^{\text{top}}(N_{T}(\mathbb{C})\backslash G(\mathbb{C}))=1$
.
We note that
![]() $N_{T}(G)(\mathbb{C})\backslash G(\mathbb{C})=(N_{T}(G)\backslash G)(\mathbb{C})$
, since
$N_{T}(G)(\mathbb{C})\backslash G(\mathbb{C})=(N_{T}(G)\backslash G)(\mathbb{C})$
, since
![]() $\mathbb{C}$
is algebraically closed. For
$\mathbb{C}$
is algebraically closed. For
![]() $\mathbb{R}$
, this is no longer the case, which makes the analysis of the Euler characteristic
$\mathbb{R}$
, this is no longer the case, which makes the analysis of the Euler characteristic
![]() $\unicode[STIX]{x1D712}^{\text{top}}((N_{T}(G)\backslash G)(\mathbb{R}))$
a bit more difficult.
$\unicode[STIX]{x1D712}^{\text{top}}((N_{T}(G)\backslash G)(\mathbb{R}))$
a bit more difficult.
Lemma 2.2. For
![]() $G=\operatorname{GL}_{n}$
or
$G=\operatorname{GL}_{n}$
or
![]() $G=\operatorname{SL}_{n}$
, we have
$G=\operatorname{SL}_{n}$
, we have
![]() $\unicode[STIX]{x1D712}^{\text{top}}((N_{T}(G)\backslash G)(\mathbb{R}))=1$
.
$\unicode[STIX]{x1D712}^{\text{top}}((N_{T}(G)\backslash G)(\mathbb{R}))=1$
.
Proof. It suffices to consider the case
![]() $G=\operatorname{GL}_{n}$
, since the schemes
$G=\operatorname{GL}_{n}$
, since the schemes
![]() $N_{T}(\operatorname{GL}_{n})\backslash \operatorname{GL}_{n}$
and
$N_{T}(\operatorname{GL}_{n})\backslash \operatorname{GL}_{n}$
and
![]() $N_{T}(\operatorname{SL}_{n})\backslash \operatorname{SL}_{n}$
are isomorphic. We write
$N_{T}(\operatorname{SL}_{n})\backslash \operatorname{SL}_{n}$
are isomorphic. We write
![]() $N_{T}$
for
$N_{T}$
for
![]() $N_{T}(\operatorname{GL}_{n})$
.
$N_{T}(\operatorname{GL}_{n})$
.
![]() $N_{T}=\mathbb{G}_{m}^{n}\rtimes \mathfrak{S}_{n}$
, where
$N_{T}=\mathbb{G}_{m}^{n}\rtimes \mathfrak{S}_{n}$
, where
![]() $\mathfrak{S}_{n}$
is the symmetric group, so we have
$\mathfrak{S}_{n}$
is the symmetric group, so we have
and
![]() $\mathbb{G}_{m}^{n}\backslash \operatorname{GL}_{n}$
is the open subscheme of
$\mathbb{G}_{m}^{n}\backslash \operatorname{GL}_{n}$
is the open subscheme of
![]() $(\mathbb{P}^{n-1})^{n}$
parametrizing
$(\mathbb{P}^{n-1})^{n}$
parametrizing
![]() $n$
-tuples of lines through 0 in
$n$
-tuples of lines through 0 in
![]() $\mathbb{A}^{n}$
which span
$\mathbb{A}^{n}$
which span
![]() $\mathbb{A}^{n}$
. This realizes
$\mathbb{A}^{n}$
. This realizes
![]() $N_{T}\backslash \operatorname{GL}_{n}$
as an open subscheme of
$N_{T}\backslash \operatorname{GL}_{n}$
as an open subscheme of
![]() $\operatorname{Sym}^{n}\mathbb{P}^{n-1}$
, and gives a decomposition of the
$\operatorname{Sym}^{n}\mathbb{P}^{n-1}$
, and gives a decomposition of the
![]() $\mathbb{R}$
-points
$\mathbb{R}$
-points
![]() $x\in (N_{T}\backslash \operatorname{GL}_{n})(\mathbb{R})$
in terms of the residue fields of the corresponding closed points
$x\in (N_{T}\backslash \operatorname{GL}_{n})(\mathbb{R})$
in terms of the residue fields of the corresponding closed points
![]() $y_{1},\ldots ,y_{s}$
of
$y_{1},\ldots ,y_{s}$
of
![]() $(\mathbb{P}^{n-1})^{n}$
lying over
$(\mathbb{P}^{n-1})^{n}$
lying over
![]() $x$
. This decomposes
$x$
. This decomposes
![]() $(N_{T}\backslash \operatorname{GL}_{n})(\mathbb{R})$
as a disjoint union of open submanifolds
$(N_{T}\backslash \operatorname{GL}_{n})(\mathbb{R})$
as a disjoint union of open submanifolds
where
![]() $U_{i}$
parametrizes the collection of lines with exactly
$U_{i}$
parametrizes the collection of lines with exactly
![]() $i$
real lines. Of course
$i$
real lines. Of course
![]() $U_{i}$
is empty if
$U_{i}$
is empty if
![]() $n-i$
is odd.
$n-i$
is odd.
We claim that
![]() $\unicode[STIX]{x1D712}^{\text{top}}(U_{i})=0$
if
$\unicode[STIX]{x1D712}^{\text{top}}(U_{i})=0$
if
![]() $i\geqslant 2$
. Indeed, we can form a finite covering space
$i\geqslant 2$
. Indeed, we can form a finite covering space
![]() $\tilde{U} _{i}\rightarrow U_{i}$
by killing the permutation action on the real lines and choosing an orientation on each real line. Then putting a metric on
$\tilde{U} _{i}\rightarrow U_{i}$
by killing the permutation action on the real lines and choosing an orientation on each real line. Then putting a metric on
![]() $\mathbb{C}^{n}$
, we see that
$\mathbb{C}^{n}$
, we see that
![]() $\tilde{U} _{i}$
is homotopy equivalent to an
$\tilde{U} _{i}$
is homotopy equivalent to an
![]() $\text{SO}(i)$
-bundle over the space parametrizing the (unordered) collection of the remaining lines. Since
$\text{SO}(i)$
-bundle over the space parametrizing the (unordered) collection of the remaining lines. Since
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\text{SO}(i))=0$
for
$\unicode[STIX]{x1D712}^{\text{top}}(\text{SO}(i))=0$
for
![]() $i\geqslant 2$
, we have
$i\geqslant 2$
, we have
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\tilde{U} _{i})=0$
and hence
$\unicode[STIX]{x1D712}^{\text{top}}(\tilde{U} _{i})=0$
and hence
![]() $\unicode[STIX]{x1D712}^{\text{top}}(U_{i})=0$
as well.
$\unicode[STIX]{x1D712}^{\text{top}}(U_{i})=0$
as well.
Now assume
![]() $n=2m$
is even.
$n=2m$
is even.
![]() $U_{0}$
parametrizes the unordered collections of
$U_{0}$
parametrizes the unordered collections of
![]() $m$
pairs of complex conjugate lines that span
$m$
pairs of complex conjugate lines that span
![]() $\mathbb{C}^{n}$
, so we may form the degree
$\mathbb{C}^{n}$
, so we may form the degree
![]() $m!$
covering space
$m!$
covering space
![]() $\tilde{U} _{0}\rightarrow U_{0}$
of ordered
$\tilde{U} _{0}\rightarrow U_{0}$
of ordered
![]() $m$
-tuples of such conjugate pairs. Each pair
$m$
-tuples of such conjugate pairs. Each pair
![]() $\ell ,\bar{\ell }$
spans a
$\ell ,\bar{\ell }$
spans a
![]() $\mathbb{A}^{2}\subset \mathbb{A}^{n}$
defined over
$\mathbb{A}^{2}\subset \mathbb{A}^{n}$
defined over
![]() $\mathbb{R}$
, so we may map
$\mathbb{R}$
, so we may map
![]() $\tilde{U} _{0}$
to the real points of the quotient
$\tilde{U} _{0}$
to the real points of the quotient
![]() $(\operatorname{GL}_{2})^{m}\backslash \operatorname{GL}_{n}$
, which is homotopy equivalent to the real points of the partial flag manifold
$(\operatorname{GL}_{2})^{m}\backslash \operatorname{GL}_{n}$
, which is homotopy equivalent to the real points of the partial flag manifold
![]() $Fl_{m}:=P_{m}\backslash \operatorname{GL}_{n}$
, where
$Fl_{m}:=P_{m}\backslash \operatorname{GL}_{n}$
, where
![]() $P_{m}$
is the parabolic with Levi subgroup
$P_{m}$
is the parabolic with Levi subgroup
![]() $(\operatorname{GL}_{2}(\mathbb{C}))^{m}$
. In fact, the map
$(\operatorname{GL}_{2}(\mathbb{C}))^{m}$
. In fact, the map
![]() $\tilde{U} _{0}\rightarrow Fl_{m}(\mathbb{R})$
is also a homotopy equivalence: given a two-plane
$\tilde{U} _{0}\rightarrow Fl_{m}(\mathbb{R})$
is also a homotopy equivalence: given a two-plane
![]() $\unicode[STIX]{x1D70B}\subset \mathbb{A}^{n}$
defined over
$\unicode[STIX]{x1D70B}\subset \mathbb{A}^{n}$
defined over
![]() $\mathbb{R}$
, the pairs of conjugate lines in
$\mathbb{R}$
, the pairs of conjugate lines in
![]() $\unicode[STIX]{x1D70B}$
are parametrized by the upper half-plane in the Riemann sphere
$\unicode[STIX]{x1D70B}$
are parametrized by the upper half-plane in the Riemann sphere
![]() $\mathbb{P}(\unicode[STIX]{x1D70B})$
, which is contractible.
$\mathbb{P}(\unicode[STIX]{x1D70B})$
, which is contractible.
We claim that
![]() $\unicode[STIX]{x1D712}^{\text{top}}(Fl_{m}(\mathbb{R}))=m!$
for all
$\unicode[STIX]{x1D712}^{\text{top}}(Fl_{m}(\mathbb{R}))=m!$
for all
![]() $m\geqslant 2$
. To compute the Euler characteristic, we use the following fact:
$m\geqslant 2$
. To compute the Euler characteristic, we use the following fact:
If
![]() $X\in \mathbf{Sm}/\mathbb{R}$
is cellular, that is,
$X\in \mathbf{Sm}/\mathbb{R}$
is cellular, that is,
![]() $X$
admits a finite stratification by locally closed subschemes
$X$
admits a finite stratification by locally closed subschemes
![]() $X_{i}\cong \mathbb{A}^{n_{i}}$
, then
$X_{i}\cong \mathbb{A}^{n_{i}}$
, then
![]() $\unicode[STIX]{x1D712}^{\text{top}}(X(\mathbb{R}))=\operatorname{rnk}\,\text{CH}^{\text{even}}(X)-\operatorname{rnk}\,\text{CH}^{\text{odd}}(X)$
.
$\unicode[STIX]{x1D712}^{\text{top}}(X(\mathbb{R}))=\operatorname{rnk}\,\text{CH}^{\text{even}}(X)-\operatorname{rnk}\,\text{CH}^{\text{odd}}(X)$
.
This follows from [Reference Levine25, Remark 1.11, Proposition 1.14], using the
![]() $\operatorname{GW}(\mathbb{R})$
-valued Euler characteristic
$\operatorname{GW}(\mathbb{R})$
-valued Euler characteristic
![]() $\unicode[STIX]{x1D712}(X/\mathbb{R})$
:
$\unicode[STIX]{x1D712}(X/\mathbb{R})$
:
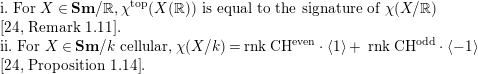 $$\begin{eqnarray}\begin{array}{@{}l@{}}\text{i}.\text{ For }X\in \mathbf{Sm}/\mathbb{R},\unicode[STIX]{x1D712}^{\text{top}}(X(\mathbb{R}))\text{ is equal to the signature of }\unicode[STIX]{x1D712}(X/\mathbb{R})\\ \text{[24, Remark 1.11]}.\\ \text{i}\text{i}.\text{ For }X\in \mathbf{Sm}/k\text{ cellular},\unicode[STIX]{x1D712}(X/k)=\operatorname{rnk}\,\text{CH}^{\text{even}}\cdot \langle 1\rangle +\,\operatorname{rnk}\,\text{CH}^{\text{odd}}\cdot \langle -1\rangle \\ \text{[24, Proposition 1.14]}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\text{i}.\text{ For }X\in \mathbf{Sm}/\mathbb{R},\unicode[STIX]{x1D712}^{\text{top}}(X(\mathbb{R}))\text{ is equal to the signature of }\unicode[STIX]{x1D712}(X/\mathbb{R})\\ \text{[24, Remark 1.11]}.\\ \text{i}\text{i}.\text{ For }X\in \mathbf{Sm}/k\text{ cellular},\unicode[STIX]{x1D712}(X/k)=\operatorname{rnk}\,\text{CH}^{\text{even}}\cdot \langle 1\rangle +\,\operatorname{rnk}\,\text{CH}^{\text{odd}}\cdot \langle -1\rangle \\ \text{[24, Proposition 1.14]}.\end{array}\end{eqnarray}$$
Alternatively, one can apply the Lefschetz trace formula to complex conjugation
![]() $c$
acting on
$c$
acting on
![]() $H^{\ast }(X(\mathbb{C}),\mathbb{Q})$
, and use the fact that for
$H^{\ast }(X(\mathbb{C}),\mathbb{Q})$
, and use the fact that for
![]() $X$
cellular,
$X$
cellular,
![]() $H^{\text{odd}}(X(\mathbb{C}),\mathbb{Q})=0$
,
$H^{\text{odd}}(X(\mathbb{C}),\mathbb{Q})=0$
,
![]() $H^{2n}(X(\mathbb{C}),\mathbb{Q})$
has dimension
$H^{2n}(X(\mathbb{C}),\mathbb{Q})$
has dimension
![]() $\operatorname{rnk}\,\text{CH}^{n}(X)$
and
$\operatorname{rnk}\,\text{CH}^{n}(X)$
and
![]() $c$
acts by
$c$
acts by
![]() $(-1)^{n}$
, since the cycle class map
$(-1)^{n}$
, since the cycle class map
![]() $\text{cl}^{n}$
is a
$\text{cl}^{n}$
is a
![]() $c$
-equivariant isomorphism from the
$c$
-equivariant isomorphism from the
![]() $c$
-invariant
$c$
-invariant
![]() $\mathbb{Q}$
vector space
$\mathbb{Q}$
vector space
![]() $\text{CH}^{n}(X)\otimes \mathbb{Q}$
to
$\text{CH}^{n}(X)\otimes \mathbb{Q}$
to
![]() $H^{2n}(X(\mathbb{C}),\mathbb{Q}(2\unicode[STIX]{x1D70B}i)^{n})=\mathbb{Q}\cdot \text{cl}^{n}(\text{CH}^{n}(X))$
.
$H^{2n}(X(\mathbb{C}),\mathbb{Q}(2\unicode[STIX]{x1D70B}i)^{n})=\mathbb{Q}\cdot \text{cl}^{n}(\text{CH}^{n}(X))$
.
For
![]() $m=2$
,
$m=2$
,
![]() $Fl_{2}=\operatorname{Gr}(2,4)$
, which has 4 Schubert cells of even dimension and 2 of odd dimension. Thus
$Fl_{2}=\operatorname{Gr}(2,4)$
, which has 4 Schubert cells of even dimension and 2 of odd dimension. Thus
![]() $\unicode[STIX]{x1D712}(Fl_{2}/\mathbb{R})=4\langle 1\rangle +2\langle -1\rangle$
, which has signature 2, and hence
$\unicode[STIX]{x1D712}(Fl_{2}/\mathbb{R})=4\langle 1\rangle +2\langle -1\rangle$
, which has signature 2, and hence
![]() $\unicode[STIX]{x1D712}^{\text{top}}(Fl_{2}(\mathbb{R}))=2$
.
$\unicode[STIX]{x1D712}^{\text{top}}(Fl_{2}(\mathbb{R}))=2$
.
In general, we have the fibration
![]() $Fl_{m}\rightarrow Fl_{m-1}$
with fiber
$Fl_{m}\rightarrow Fl_{m-1}$
with fiber
![]() $\operatorname{Gr}(2,2m)$
. We can compare the Schubert cells for
$\operatorname{Gr}(2,2m)$
. We can compare the Schubert cells for
![]() $\operatorname{Gr}(2,2m)$
with those for
$\operatorname{Gr}(2,2m)$
with those for
![]() $\operatorname{Gr}(2,2m-2)$
: the “new” ones come from the partitions
$\operatorname{Gr}(2,2m-2)$
: the “new” ones come from the partitions
![]() $(2m-3,i)$
,
$(2m-3,i)$
,
![]() $i=0,\ldots ,2m-3$
and
$i=0,\ldots ,2m-3$
and
![]() $(2m-2,i)$
,
$(2m-2,i)$
,
![]() $i=0,\ldots ,2m-2$
. This adds the quadratic form
$i=0,\ldots ,2m-2$
. This adds the quadratic form
![]() $(2m-1)\langle 1\rangle +(2m-2)\langle -1\rangle$
of signature +1 to
$(2m-1)\langle 1\rangle +(2m-2)\langle -1\rangle$
of signature +1 to
![]() $\unicode[STIX]{x1D712}(\operatorname{Gr}(2,2m-2))$
, which implies that
$\unicode[STIX]{x1D712}(\operatorname{Gr}(2,2m-2))$
, which implies that
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m)(\mathbb{R}))=\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m-2))+1$
. By induction, this says that
$\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m)(\mathbb{R}))=\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m-2))+1$
. By induction, this says that
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m)(\mathbb{R}))=m$
, and similarly by induction we find
$\unicode[STIX]{x1D712}^{\text{top}}(\operatorname{Gr}(2,2m)(\mathbb{R}))=m$
, and similarly by induction we find
![]() $\unicode[STIX]{x1D712}^{\text{top}}(Fl_{m})=m\cdot \unicode[STIX]{x1D712}^{\text{top}}(Fl_{m-1})=m!$
. Thus
$\unicode[STIX]{x1D712}^{\text{top}}(Fl_{m})=m\cdot \unicode[STIX]{x1D712}^{\text{top}}(Fl_{m-1})=m!$
. Thus
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\tilde{U} _{0})=m!$
and hence
$\unicode[STIX]{x1D712}^{\text{top}}(\tilde{U} _{0})=m!$
and hence
![]() $\unicode[STIX]{x1D712}^{\text{top}}(U_{0})=1$
.
$\unicode[STIX]{x1D712}^{\text{top}}(U_{0})=1$
.
In case
![]() $n=2m+1$
is odd, we can again choose a metric and fiber
$n=2m+1$
is odd, we can again choose a metric and fiber
![]() $U_{1}$
over the real projective space
$U_{1}$
over the real projective space
![]() $\mathbb{R}\mathbb{P}^{2m}$
, with fiber over
$\mathbb{R}\mathbb{P}^{2m}$
, with fiber over
![]() $[\ell ]\in \mathbb{R}\mathbb{P}^{2m}$
homotopy equivalent to the
$[\ell ]\in \mathbb{R}\mathbb{P}^{2m}$
homotopy equivalent to the
![]() $U_{0}$
for the hyperplane perpendicular to the
$U_{0}$
for the hyperplane perpendicular to the
![]() $\mathbb{C}$
-span of
$\mathbb{C}$
-span of
![]() $\ell$
. As
$\ell$
. As
![]() $\unicode[STIX]{x1D712}^{\text{top}}(\mathbb{R}\mathbb{P}^{2m})=1$
, this yields
$\unicode[STIX]{x1D712}^{\text{top}}(\mathbb{R}\mathbb{P}^{2m})=1$
, this yields
![]() $\unicode[STIX]{x1D712}^{\text{top}}(U_{1})=1$
.
$\unicode[STIX]{x1D712}^{\text{top}}(U_{1})=1$
.
Proposition 2.3. Let
![]() $n\geqslant 1$
be an integer. There is a 4-torsion element
$n\geqslant 1$
be an integer. There is a 4-torsion element
![]() $\unicode[STIX]{x1D70F}_{n}\in \operatorname{GW}(\mathbb{Q})$
with
$\unicode[STIX]{x1D70F}_{n}\in \operatorname{GW}(\mathbb{Q})$
with
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})=1+\unicode[STIX]{x1D70F}_{n}$
. Moreover, the Euler characteristic
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})=1+\unicode[STIX]{x1D70F}_{n}$
. Moreover, the Euler characteristic
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
is invertible in
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
is invertible in
![]() $\operatorname{GW}(\mathbb{Q})$
.
$\operatorname{GW}(\mathbb{Q})$
.
Proof. From Lemma 2.2 and (2.1)(i),
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
has signature 1. Moreover, the rank of
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
has signature 1. Moreover, the rank of
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
is
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})$
is
![]() $\unicode[STIX]{x1D712}^{\text{top}}((N_{T}\backslash \operatorname{GL}_{n})(\mathbb{C}))=1$
and thus
$\unicode[STIX]{x1D712}^{\text{top}}((N_{T}\backslash \operatorname{GL}_{n})(\mathbb{C}))=1$
and thus
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})-1\in \operatorname{GW}(\mathbb{Q})$
has rank and signature zero. The Witt ring of
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{n})/\mathbb{Q})-1\in \operatorname{GW}(\mathbb{Q})$
has rank and signature zero. The Witt ring of
![]() $\mathbb{Q}$
is isomorphic to the direct sum
$\mathbb{Q}$
is isomorphic to the direct sum
![]() $W(\mathbb{R})\oplus \oplus _{p}W(\mathbb{F}_{p})$
[Reference Scharlau35, Chapter 5, Theorems 1.5 and 3.4] and thus an element of
$W(\mathbb{R})\oplus \oplus _{p}W(\mathbb{F}_{p})$
[Reference Scharlau35, Chapter 5, Theorems 1.5 and 3.4] and thus an element of
![]() $\operatorname{GW}(\mathbb{Q})$
with rank and signature zero lives in the direct sum of the Witt rings
$\operatorname{GW}(\mathbb{Q})$
with rank and signature zero lives in the direct sum of the Witt rings
![]() $W(\mathbb{F}_{p})$
, which are either
$W(\mathbb{F}_{p})$
, which are either
![]() $\mathbb{Z}/2$
(for
$\mathbb{Z}/2$
(for
![]() $p=2$
[Reference Scharlau35, Chapter 5, Theorem 1.6]),
$p=2$
[Reference Scharlau35, Chapter 5, Theorem 1.6]),
![]() $\mathbb{Z}/2\times \mathbb{Z}/2$
or
$\mathbb{Z}/2\times \mathbb{Z}/2$
or
![]() $\mathbb{Z}/4$
[Reference Scharlau35, Chapter 2, Corollary 3.11]. As the kernel
$\mathbb{Z}/4$
[Reference Scharlau35, Chapter 2, Corollary 3.11]. As the kernel
![]() $I$
of
$I$
of
![]() $\operatorname{GW}(\mathbb{Q})\rightarrow \operatorname{GW}(\mathbb{R})$
satisfies
$\operatorname{GW}(\mathbb{Q})\rightarrow \operatorname{GW}(\mathbb{R})$
satisfies
![]() $I^{3}=0$
[Reference Scharlau35, Chapter 5, Theorems 1.5, 3.4 and 6.6], an element of
$I^{3}=0$
[Reference Scharlau35, Chapter 5, Theorems 1.5, 3.4 and 6.6], an element of
![]() $\operatorname{GW}(\mathbb{Q})$
with rank and signature one is invertible.
$\operatorname{GW}(\mathbb{Q})$
with rank and signature one is invertible.
Corollary 2.4. The weak form of Conjecture 2.1 holds for
![]() $G=\operatorname{GL}_{n}$
and
$G=\operatorname{GL}_{n}$
and
![]() $G=\operatorname{SL}_{n}$
over a field
$G=\operatorname{SL}_{n}$
over a field
![]() $k$
of characteristic zero.
$k$
of characteristic zero.
We take the opportunity here to make explicit our model for
![]() $BG$
,
$BG$
,
![]() $G$
a reductive group scheme over a perfect field
$G$
a reductive group scheme over a perfect field
![]() $k$
. We follow Morel–Voevodsky [Reference Morel and Voevodsky32, Section 4.2.2], by using the Totaro–Graham–Edidin model for the Morel–Voevodsky
$k$
. We follow Morel–Voevodsky [Reference Morel and Voevodsky32, Section 4.2.2], by using the Totaro–Graham–Edidin model for the Morel–Voevodsky
![]() $B_{\acute{\text{e}}\text{t}}G$
as our
$B_{\acute{\text{e}}\text{t}}G$
as our
![]() $BG$
.
$BG$
.
Fixing integers
![]() $n>0$
,
$n>0$
,
![]() $m\geqslant 0$
, let
$m\geqslant 0$
, let
![]() $M_{n\times m+n}\cong \mathbb{A}^{n(m+n)}$
be the affine space of
$M_{n\times m+n}\cong \mathbb{A}^{n(m+n)}$
be the affine space of
![]() $m\times (m+n)$
matrices and let
$m\times (m+n)$
matrices and let
![]() $E_{m}\operatorname{GL}_{n}\subset M_{n\times m+n}$
be the open subscheme of the matrices of maximal rank
$E_{m}\operatorname{GL}_{n}\subset M_{n\times m+n}$
be the open subscheme of the matrices of maximal rank
![]() $n$
. We give
$n$
. We give
![]() $E_{m}\operatorname{GL}_{n}$
the base-point
$E_{m}\operatorname{GL}_{n}$
the base-point
![]() $x_{0}=(I_{n},0_{n},\ldots ,0_{n})$
where
$x_{0}=(I_{n},0_{n},\ldots ,0_{n})$
where
![]() $I_{n}\in M_{n\times n}$
is the identity matrix and
$I_{n}\in M_{n\times n}$
is the identity matrix and
![]() $0_{n}\in M_{n\times 1}$
is the 0-matrix. We let
$0_{n}\in M_{n\times 1}$
is the 0-matrix. We let
![]() $E\operatorname{GL}_{n}$
be the presheaf on
$E\operatorname{GL}_{n}$
be the presheaf on
![]() $\mathbf{Sm}/k$
$\mathbf{Sm}/k$
which we may consider as a pointed presheaf with base-point
![]() $x_{0}$
if we wish. We note that
$x_{0}$
if we wish. We note that
![]() $\operatorname{GL}_{n}$
acts freely on
$\operatorname{GL}_{n}$
acts freely on
![]() $E_{m}\operatorname{GL}_{n}$
for each
$E_{m}\operatorname{GL}_{n}$
for each
![]() $m\geqslant 0$
. Fixing an embedding
$m\geqslant 0$
. Fixing an embedding
![]() $G\subset \operatorname{GL}_{n}$
for some
$G\subset \operatorname{GL}_{n}$
for some
![]() $n$
, we have the (pointed) quotient scheme
$n$
, we have the (pointed) quotient scheme
and the (pointed) presheaf on
![]() $\mathbf{Sm}/k$
$\mathbf{Sm}/k$
For
![]() $X\in \mathbf{Sm}/k$
, we have
$X\in \mathbf{Sm}/k$
, we have
where
![]() $B_{m}G(X)$
denotes the morphisms from
$B_{m}G(X)$
denotes the morphisms from
![]() $X$
to
$X$
to
![]() $B_{m}G$
in
$B_{m}G$
in
![]() $\mathbf{Sm}_{k}$
and
$\mathbf{Sm}_{k}$
and
![]() $BG(X)$
is the set of morphisms from the representable presheaf
$BG(X)$
is the set of morphisms from the representable presheaf
![]() $X$
to
$X$
to
![]() $BG$
. Thus we can speak of the
$BG$
. Thus we can speak of the
![]() $k$
-points of
$k$
-points of
![]() $BG$
.
$BG$
.
Although
![]() $B_{m}G$
is almost never the presheaf quotient of
$B_{m}G$
is almost never the presheaf quotient of
![]() $E_{m}\operatorname{GL}_{n}$
by
$E_{m}\operatorname{GL}_{n}$
by
![]() $G$
,
$G$
,
![]() $B_{m}G$
is the quotient
$B_{m}G$
is the quotient
![]() $G\backslash E_{m}\operatorname{GL}_{n}$
as étale sheaf, and if
$G\backslash E_{m}\operatorname{GL}_{n}$
as étale sheaf, and if
![]() $G$
is special,
$G$
is special,
![]() $B_{m}G$
is the quotient
$B_{m}G$
is the quotient
![]() $G\backslash E_{m}\operatorname{GL}_{n}$
as Zariski sheaf. These facts pass to the morphism
$G\backslash E_{m}\operatorname{GL}_{n}$
as Zariski sheaf. These facts pass to the morphism
![]() $E\operatorname{GL}_{n}\rightarrow BG$
. Although
$E\operatorname{GL}_{n}\rightarrow BG$
. Although
![]() $BG$
is not in general the presheaf quotient, we nonetheless often write
$BG$
is not in general the presheaf quotient, we nonetheless often write
![]() $BG=G\backslash E\operatorname{GL}_{n}$
. We note that the
$BG=G\backslash E\operatorname{GL}_{n}$
. We note that the
![]() $\mathbb{A}^{1}$
-homotopy type of
$\mathbb{A}^{1}$
-homotopy type of
![]() $BG$
is independent of the choice of embedding
$BG$
is independent of the choice of embedding
![]() $G\subset \operatorname{GL}_{n}$
and does in fact give a model for the Morel–Voevodsky
$G\subset \operatorname{GL}_{n}$
and does in fact give a model for the Morel–Voevodsky
![]() $B_{\acute{\text{e}}\text{t}}G$
in the unstable motivic homotopy category [Reference Morel and Voevodsky32, Remark 4.27].
$B_{\acute{\text{e}}\text{t}}G$
in the unstable motivic homotopy category [Reference Morel and Voevodsky32, Remark 4.27].
For each
![]() $m\geqslant 0$
, we have the principal
$m\geqslant 0$
, we have the principal
![]() $G$
-bundle
$G$
-bundle
which is étale locally trivial if
![]() $G$
is smooth over
$G$
is smooth over
![]() $k$
and is Zariski locally trivial if
$k$
and is Zariski locally trivial if
![]() $G$
is special. We refer to the sequence
$G$
is special. We refer to the sequence
as a principal
![]() $G$
-bundle.
$G$
-bundle.
For any
![]() $G$
defined as a closed subgroup scheme of
$G$
defined as a closed subgroup scheme of
![]() $\operatorname{GL}_{n}$
or of
$\operatorname{GL}_{n}$
or of
![]() $\operatorname{SL}_{n}$
, we always use the embedding
$\operatorname{SL}_{n}$
, we always use the embedding
![]() $G\subset \operatorname{GL}_{n}$
in our definition of
$G\subset \operatorname{GL}_{n}$
in our definition of
![]() $B_{m}G$
and
$B_{m}G$
and
![]() $BG$
, unless we explicitly say otherwise.
$BG$
, unless we explicitly say otherwise.
For
![]() $G=\operatorname{GL}_{n}$
, we recall that
$G=\operatorname{GL}_{n}$
, we recall that
![]() $B_{m}\operatorname{GL}_{n}$
is just the Grassmann scheme
$B_{m}\operatorname{GL}_{n}$
is just the Grassmann scheme
![]() $\operatorname{Gr}(n,n+m)$
. For
$\operatorname{Gr}(n,n+m)$
. For
![]() $G=N_{T}:=N_{T}(\operatorname{GL}_{n})\subset \operatorname{GL}_{n}$
we have the fiber bundle
$G=N_{T}:=N_{T}(\operatorname{GL}_{n})\subset \operatorname{GL}_{n}$
we have the fiber bundle
Since
![]() $\operatorname{GL}_{n}$
is special the bundle
$\operatorname{GL}_{n}$
is special the bundle
![]() $E_{m}\operatorname{GL}_{n}\rightarrow B_{m}\operatorname{GL}_{n}$
is a Zariski locally trivial principal
$E_{m}\operatorname{GL}_{n}\rightarrow B_{m}\operatorname{GL}_{n}$
is a Zariski locally trivial principal
![]() $\operatorname{GL}_{n}$
-bundle; this gives the description of
$\operatorname{GL}_{n}$
-bundle; this gives the description of
![]() $B_{m}N_{T}\rightarrow B_{m}\operatorname{GL}_{n}$
as
$B_{m}N_{T}\rightarrow B_{m}\operatorname{GL}_{n}$
as
that is
![]() $\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n},m}:B_{m}N_{T}\rightarrow B_{m}\operatorname{GL}_{n}$
is a Zariski locally trivial fiber bundle with fiber
$\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n},m}:B_{m}N_{T}\rightarrow B_{m}\operatorname{GL}_{n}$
is a Zariski locally trivial fiber bundle with fiber
![]() $F=N_{T}\backslash \operatorname{GL}_{n}$
.
$F=N_{T}\backslash \operatorname{GL}_{n}$
.
Applying this construction to
![]() $N_{T}(\operatorname{SL}_{n})\subset \operatorname{SL}_{n}\subset \operatorname{GL}_{n}$
, gives us the Zariski locally trivial fiber bundle
$N_{T}(\operatorname{SL}_{n})\subset \operatorname{SL}_{n}\subset \operatorname{GL}_{n}$
, gives us the Zariski locally trivial fiber bundle
with fiber
![]() $N_{T}\backslash \operatorname{GL}_{n}$
, noting that the inclusion
$N_{T}\backslash \operatorname{GL}_{n}$
, noting that the inclusion
![]() $\operatorname{SL}_{n}\rightarrow \operatorname{GL}_{n}$
induces an isomorphism of schemes
$\operatorname{SL}_{n}\rightarrow \operatorname{GL}_{n}$
induces an isomorphism of schemes
Theorem 2.5. Let
![]() $k$
be a field of characteristic zero and let
$k$
be a field of characteristic zero and let
![]() ${\mathcal{E}}\in \operatorname{SH}(k)$
be a motivic ring spectrum. Then the maps
${\mathcal{E}}\in \operatorname{SH}(k)$
be a motivic ring spectrum. Then the maps
![]() $\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n}}:B_{m}N_{T}(\operatorname{GL}_{n})\rightarrow B_{m}\operatorname{GL}_{n}$
and
$\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n}}:B_{m}N_{T}(\operatorname{GL}_{n})\rightarrow B_{m}\operatorname{GL}_{n}$
and
![]() $\unicode[STIX]{x1D70B}_{\operatorname{SL}_{n}}:B_{m}N_{T}(\operatorname{SL}_{n})\rightarrow B_{m}\operatorname{SL}_{n}$
induce split injections
$\unicode[STIX]{x1D70B}_{\operatorname{SL}_{n}}:B_{m}N_{T}(\operatorname{SL}_{n})\rightarrow B_{m}\operatorname{SL}_{n}$
induce split injections
for each
![]() $m\geqslant 0$
, and injections
$m\geqslant 0$
, and injections
Proof. We give the proof for
![]() $\operatorname{GL}_{n}$
, the proof for
$\operatorname{GL}_{n}$
, the proof for
![]() $\operatorname{SL}_{n}$
is the same; we write
$\operatorname{SL}_{n}$
is the same; we write
![]() $N_{T}$
for
$N_{T}$
for
![]() $N_{T}(\operatorname{GL}_{n})$
.
$N_{T}(\operatorname{GL}_{n})$
.
Since
![]() $k$
has characteristic zero and
$k$
has characteristic zero and
![]() $N_{T}\backslash \operatorname{GL}_{n}$
is smooth over
$N_{T}\backslash \operatorname{GL}_{n}$
is smooth over
![]() $k$
,
$k$
,
![]() $N_{T}\backslash \operatorname{GL}_{n}$
is strongly dualizable. By our computations above verifying the weak form of Conjecture 2.1, the Euler characteristic
$N_{T}\backslash \operatorname{GL}_{n}$
is strongly dualizable. By our computations above verifying the weak form of Conjecture 2.1, the Euler characteristic
![]() $\unicode[STIX]{x1D712}(N_{T}\backslash \operatorname{GL}_{n}/k)$
is invertible in
$\unicode[STIX]{x1D712}(N_{T}\backslash \operatorname{GL}_{n}/k)$
is invertible in
![]() $\operatorname{GW}(k)$
, thus by Theorem 1.10, the map
$\operatorname{GW}(k)$
, thus by Theorem 1.10, the map
is split injective, with splitting natural in
![]() $m$
.
$m$
.
This gives split injections
for
![]() $i=0,1$
, and by looking at the Milnor sequences
$i=0,1$
, and by looking at the Milnor sequences

we see that
![]() $\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n}}^{\ast }:{\mathcal{E}}^{\ast ,\ast }(\operatorname{BGL}_{n})\rightarrow {\mathcal{E}}^{\ast ,\ast }(BN_{T_{\operatorname{GL}_{n}}})$
is injective.
$\unicode[STIX]{x1D70B}_{\operatorname{GL}_{n}}^{\ast }:{\mathcal{E}}^{\ast ,\ast }(\operatorname{BGL}_{n})\rightarrow {\mathcal{E}}^{\ast ,\ast }(BN_{T_{\operatorname{GL}_{n}}})$
is injective.
We conclude this section with a proof of the strong form of the conjecture for
![]() $\operatorname{GL}_{2}$
(or
$\operatorname{GL}_{2}$
(or
![]() $\operatorname{SL}_{2}$
). We argue as above:
$\operatorname{SL}_{2}$
). We argue as above:
![]() $(\mathbb{G}_{m})^{2}\backslash \operatorname{GL}_{2}=\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
, where
$(\mathbb{G}_{m})^{2}\backslash \operatorname{GL}_{2}=\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
, where
![]() $\unicode[STIX]{x1D6E5}\cong \mathbb{P}^{1}$
is the diagonal, and thus
$\unicode[STIX]{x1D6E5}\cong \mathbb{P}^{1}$
is the diagonal, and thus
![]() $N_{T}\backslash \operatorname{GL}_{2}=\mathfrak{S}_{2}\backslash (\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5})$
. We have
$N_{T}\backslash \operatorname{GL}_{2}=\mathfrak{S}_{2}\backslash (\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5})$
. We have
![]() $\mathfrak{S}_{2}\backslash \mathbb{P}^{1}\times \mathbb{P}^{1}=\operatorname{Sym}^{2}\mathbb{P}^{1}\cong \mathbb{P}^{2}$
. Via this isomorphism the quotient map
$\mathfrak{S}_{2}\backslash \mathbb{P}^{1}\times \mathbb{P}^{1}=\operatorname{Sym}^{2}\mathbb{P}^{1}\cong \mathbb{P}^{2}$
. Via this isomorphism the quotient map
is given by symmetric functions,
Thus the restriction of
![]() $p$
to
$p$
to
![]() $\unicode[STIX]{x1D6E5}$
is the map
$\unicode[STIX]{x1D6E5}$
is the map
![]() $\bar{\unicode[STIX]{x1D70B}}([x_{0}:x_{1}])=[x_{0}^{2}:2x_{0}x_{1}:x_{1}^{2}]$
with image the conic
$\bar{\unicode[STIX]{x1D70B}}([x_{0}:x_{1}])=[x_{0}^{2}:2x_{0}x_{1}:x_{1}^{2}]$
with image the conic
![]() $C\subset \mathbb{P}^{2}$
defined by
$C\subset \mathbb{P}^{2}$
defined by
![]() $Q:=T_{1}^{2}-4T_{0}T_{2}$
. Furthermore, this identifies the double cover
$Q:=T_{1}^{2}-4T_{0}T_{2}$
. Furthermore, this identifies the double cover
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{2}$
with
$\mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{2}$
with
![]() $\text{Spec }{\mathcal{O}}_{\mathbb{P}^{2}}(\sqrt{Q})$
, that is, the closed subscheme of
$\text{Spec }{\mathcal{O}}_{\mathbb{P}^{2}}(\sqrt{Q})$
, that is, the closed subscheme of
![]() $O_{\mathbb{P}^{2}}(1)$
defined by pulling back the section of
$O_{\mathbb{P}^{2}}(1)$
defined by pulling back the section of
![]() $O_{\mathbb{P}^{2}}(2)$
defined by
$O_{\mathbb{P}^{2}}(2)$
defined by
![]() $Q$
via the squaring map
$Q$
via the squaring map
![]() $O_{\mathbb{P}^{2}}(1)\rightarrow O_{\mathbb{P}^{2}}(2)$
.
$O_{\mathbb{P}^{2}}(1)\rightarrow O_{\mathbb{P}^{2}}(2)$
.
For
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
, the map
$\neq 2$
, the map
![]() $\bar{\unicode[STIX]{x1D70B}}:\mathbb{P}^{1}\rightarrow C$
is an isomorphism. If
$\bar{\unicode[STIX]{x1D70B}}:\mathbb{P}^{1}\rightarrow C$
is an isomorphism. If
![]() $\text{char}k=2$
, then
$\text{char}k=2$
, then
![]() $C$
is just the line
$C$
is just the line
![]() $T_{1}=0$
and
$T_{1}=0$
and
![]() $N_{T}\backslash \operatorname{GL}_{2}\cong \mathbb{A}^{2}$
.
$N_{T}\backslash \operatorname{GL}_{2}\cong \mathbb{A}^{2}$
.
We have the
![]() $\mathbb{A}^{1}$
- cofiber sequence
$\mathbb{A}^{1}$
- cofiber sequence
![]() $\mathbb{P}^{2}-C{\hookrightarrow}\mathbb{P}^{2}\rightarrow \operatorname{Th}(N_{C/\mathbb{P}^{2}})$
. The identity
$\mathbb{P}^{2}-C{\hookrightarrow}\mathbb{P}^{2}\rightarrow \operatorname{Th}(N_{C/\mathbb{P}^{2}})$
. The identity
![]() $\unicode[STIX]{x1D712}(Th(N_{C/\mathbb{P}^{2}})/k)=\langle -1\rangle \unicode[STIX]{x1D712}(C/k)$
[Reference Levine25, Proposition 1.10(2)] together with the additivity of
$\unicode[STIX]{x1D712}(Th(N_{C/\mathbb{P}^{2}})/k)=\langle -1\rangle \unicode[STIX]{x1D712}(C/k)$
[Reference Levine25, Proposition 1.10(2)] together with the additivity of
![]() $\unicode[STIX]{x1D712}(-/k)$
in distinguished triangles gives
$\unicode[STIX]{x1D712}(-/k)$
in distinguished triangles gives
Applying (2.1)(ii), this gives
verifying the strong form of the conjecture in this case.
Proposition 2.6. For
![]() $k$
a perfect field,
$k$
a perfect field,
![]() $\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{2})/k)=1$
.
$\unicode[STIX]{x1D712}((N_{T}\backslash \operatorname{GL}_{2})/k)=1$
.
3 Some background on Euler and Pontryagin classes
We now turn to a more detailed study of Euler classes and Pontryagin classes. In this section we recall some necessary background on characteristic classes, which we use throughout the rest of the paper. This material is all taken from [Reference Ananyevskiy3].
We work over a fixed perfect base field
![]() $k$
, giving us the motivic stable homotopy category
$k$
, giving us the motivic stable homotopy category
![]() $\operatorname{SH}(k)$
as the setting for our constructions.
$\operatorname{SH}(k)$
as the setting for our constructions.
We have the algebraic Hopf map
![]() $\unicode[STIX]{x1D702}_{2}:\mathbb{A}^{2}-\{0\}\rightarrow \mathbb{P}^{1}$
, giving the stable Hopf map
$\unicode[STIX]{x1D702}_{2}:\mathbb{A}^{2}-\{0\}\rightarrow \mathbb{P}^{1}$
, giving the stable Hopf map
![]() $\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6F4}_{\mathbb{G}_{m}}\mathbb{S}_{k}\rightarrow \mathbb{S}_{k}$
, that is
$\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6F4}_{\mathbb{G}_{m}}\mathbb{S}_{k}\rightarrow \mathbb{S}_{k}$
, that is
![]() $\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D70B}_{1,1}(\mathbb{S}_{k})(k)$
. For
$\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D70B}_{1,1}(\mathbb{S}_{k})(k)$
. For
![]() ${\mathcal{E}}$
a motivic ring spectrum, the unit map gives us the element
${\mathcal{E}}$
a motivic ring spectrum, the unit map gives us the element
![]() $\unicode[STIX]{x1D702}_{{\mathcal{E}}}\in {\mathcal{E}}^{-1,-1}(k)$
.
$\unicode[STIX]{x1D702}_{{\mathcal{E}}}\in {\mathcal{E}}^{-1,-1}(k)$
.
![]() ${\mathcal{E}}$
is said to be an
${\mathcal{E}}$
is said to be an
![]() $\unicode[STIX]{x1D702}$
-invertible theory if multiplication by
$\unicode[STIX]{x1D702}$
-invertible theory if multiplication by
![]() $\unicode[STIX]{x1D702}_{{\mathcal{E}}}$
is invertible on
$\unicode[STIX]{x1D702}_{{\mathcal{E}}}$
is invertible on
![]() ${\mathcal{E}}^{\ast \ast }(k)$
, that is, there is an element
${\mathcal{E}}^{\ast \ast }(k)$
, that is, there is an element
![]() $\unicode[STIX]{x1D702}_{{\mathcal{E}}}^{-1}\in {\mathcal{E}}^{1,1}(k)$
with
$\unicode[STIX]{x1D702}_{{\mathcal{E}}}^{-1}\in {\mathcal{E}}^{1,1}(k)$
with
![]() $\unicode[STIX]{x1D702}_{{\mathcal{E}}}\cdot \unicode[STIX]{x1D702}_{{\mathcal{E}}}^{-1}=1_{{\mathcal{E}}}$
. This implies that multiplication by
$\unicode[STIX]{x1D702}_{{\mathcal{E}}}\cdot \unicode[STIX]{x1D702}_{{\mathcal{E}}}^{-1}=1_{{\mathcal{E}}}$
. This implies that multiplication by
![]() $\unicode[STIX]{x1D702}_{{\mathcal{E}}}$
is an isomorphism on
$\unicode[STIX]{x1D702}_{{\mathcal{E}}}$
is an isomorphism on
![]() ${\mathcal{E}}^{\ast \ast }(F)$
for all
${\mathcal{E}}^{\ast \ast }(F)$
for all
![]() $F\in \operatorname{SH}(k)$
.
$F\in \operatorname{SH}(k)$
.
We take the definition of an
![]() $\operatorname{SL}$
-orientation on
$\operatorname{SL}$
-orientation on
![]() ${\mathcal{E}}$
from [Reference Ananyevskiy3, Definition 4], for us an
${\mathcal{E}}$
from [Reference Ananyevskiy3, Definition 4], for us an
![]() $\operatorname{SL}$
-orientation is always normalized in the sense of loc. cit.
$\operatorname{SL}$
-orientation is always normalized in the sense of loc. cit.
Following [Reference Ananyevskiy3, Definition 1], an
![]() $\operatorname{SL}_{n}$
-bundle on some
$\operatorname{SL}_{n}$
-bundle on some
![]() $X\in \mathbf{Sm}/k$
is a vector bundle
$X\in \mathbf{Sm}/k$
is a vector bundle
![]() $E\rightarrow X$
together with an isomorphism
$E\rightarrow X$
together with an isomorphism
![]() $\unicode[STIX]{x1D703}:\operatorname{det}E\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{X}$
. We use as well the definition of the Euler class
$\unicode[STIX]{x1D703}:\operatorname{det}E\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{X}$
. We use as well the definition of the Euler class
![]() $e(E,\unicode[STIX]{x1D703})\in {\mathcal{E}}^{2n,n}(X)$
of an
$e(E,\unicode[STIX]{x1D703})\in {\mathcal{E}}^{2n,n}(X)$
of an
![]() $\operatorname{SL}_{n}$
-bundle in an
$\operatorname{SL}_{n}$
-bundle in an
![]() $\operatorname{SL}$
-oriented theory
$\operatorname{SL}$
-oriented theory
![]() ${\mathcal{E}}$
[Reference Ananyevskiy3, Definition 4], and the Pontryagin classes
${\mathcal{E}}$
[Reference Ananyevskiy3, Definition 4], and the Pontryagin classes
![]() $p_{m}(E)\in {\mathcal{E}}^{4m,2m}(X)$
of an arbitrary vector bundle
$p_{m}(E)\in {\mathcal{E}}^{4m,2m}(X)$
of an arbitrary vector bundle
![]() $E\rightarrow X$
, for an
$E\rightarrow X$
, for an
![]() $\operatorname{SL}$
-oriented,
$\operatorname{SL}$
-oriented,
![]() $\unicode[STIX]{x1D702}$
-invertible theory
$\unicode[STIX]{x1D702}$
-invertible theory
![]() ${\mathcal{E}}$
[Reference Ananyevskiy3, Definition 19].
${\mathcal{E}}$
[Reference Ananyevskiy3, Definition 19].
For an
![]() $\operatorname{SL}$
-oriented theory
$\operatorname{SL}$
-oriented theory
![]() ${\mathcal{E}}$
and a line bundle
${\mathcal{E}}$
and a line bundle
![]() $L\rightarrow X$
,
$L\rightarrow X$
,
![]() $X\in \mathbf{Sm}/k$
, one has the twisted cohomology
$X\in \mathbf{Sm}/k$
, one has the twisted cohomology
The Euler class for
![]() $\operatorname{SL}_{n}$
bundles extends to a theory of Euler classes
$\operatorname{SL}_{n}$
bundles extends to a theory of Euler classes
for arbitrary rank
![]() $n$
vector bundles
$n$
vector bundles
![]() $E\rightarrow X$
,
$E\rightarrow X$
,
![]() $X\in \mathbf{Sm}/k$
as follows: let
$X\in \mathbf{Sm}/k$
as follows: let
![]() $L=\operatorname{det}E\rightarrow X$
. One has a canonical trivialization of
$L=\operatorname{det}E\rightarrow X$
. One has a canonical trivialization of
![]() $\operatorname{det}(E\oplus L^{-1})$
, giving the Thom class
$\operatorname{det}(E\oplus L^{-1})$
, giving the Thom class
![]() $\operatorname{th}(E\oplus L^{-1},can)\in {\mathcal{E}}_{0_{E\oplus L^{-1}}}^{2n+2,n+1}(E\oplus L^{-1})$
. Pulling back by the inclusion
$\operatorname{th}(E\oplus L^{-1},can)\in {\mathcal{E}}_{0_{E\oplus L^{-1}}}^{2n+2,n+1}(E\oplus L^{-1})$
. Pulling back by the inclusion
![]() $i:L^{-1}=0_{X}\oplus L^{-1}\rightarrow E\oplus L^{-1}$
gives the class
$i:L^{-1}=0_{X}\oplus L^{-1}\rightarrow E\oplus L^{-1}$
gives the class
For details and properties of the twisted cohomology for
![]() $\operatorname{SL}$
-oriented theories, we refer the reader to [Reference Levine and Raksit26, § 3] and [Reference Ananyevskiy1, § 3].
$\operatorname{SL}$
-oriented theories, we refer the reader to [Reference Levine and Raksit26, § 3] and [Reference Ananyevskiy1, § 3].
For an
![]() $\text{SL}_{n}$
-bundle
$\text{SL}_{n}$
-bundle
![]() $E\rightarrow X$
, we have the total Pontryagin class
$E\rightarrow X$
, we have the total Pontryagin class
![]() $p(E)=1+\sum _{i\geqslant 1}p_{i}(E)\in {\mathcal{E}}^{4\ast ,2\ast }(X)$
, which satisfies the Whitney formula for
$p(E)=1+\sum _{i\geqslant 1}p_{i}(E)\in {\mathcal{E}}^{4\ast ,2\ast }(X)$
, which satisfies the Whitney formula for
![]() $\operatorname{SL}$
-bundles: if
$\operatorname{SL}$
-bundles: if
is an exact sequence of
![]() $\operatorname{SL}$
-vector bundles on
$\operatorname{SL}$
-vector bundles on
![]() $X\in \mathbf{Sm}/k$
, then
$X\in \mathbf{Sm}/k$
, then
In addition, for an
![]() $\operatorname{SL}$
bundle
$\operatorname{SL}$
bundle
![]() $E$
of rank
$E$
of rank
![]() $n$
,
$n$
,
![]() $p_{i}(E)=0$
for
$p_{i}(E)=0$
for
![]() $2i>n$
. These facts follow from [Reference Ananyevskiy3, Corollary 3, Lemma 15]. For theories
$2i>n$
. These facts follow from [Reference Ananyevskiy3, Corollary 3, Lemma 15]. For theories
![]() ${\mathcal{E}}$
which are
${\mathcal{E}}$
which are
![]() $\operatorname{SL}$
-oriented and
$\operatorname{SL}$
-oriented and
![]() $\unicode[STIX]{x1D702}$
-invertible, these facts hold for arbitrary vector bundles and arbitrary short exact sequences of vector bundles [Reference Ananyevskiy1, Corollary 7.9].
$\unicode[STIX]{x1D702}$
-invertible, these facts hold for arbitrary vector bundles and arbitrary short exact sequences of vector bundles [Reference Ananyevskiy1, Corollary 7.9].
Remark 3.1. As explained in [Reference Fasel and Srinivas17], the Eilenberg–MacLane spectrum associated to the graded sheaf of Milnor–Witt sheaves
![]() ${\mathcal{K}}_{\ast }^{MW}$
admits Thom classes for bundles with a trivialized determinant, hence
${\mathcal{K}}_{\ast }^{MW}$
admits Thom classes for bundles with a trivialized determinant, hence
![]() $\operatorname{EM}({\mathcal{K}}_{\ast }^{MW})$
defines an
$\operatorname{EM}({\mathcal{K}}_{\ast }^{MW})$
defines an
![]() $\operatorname{SL}$
-oriented theory. Since
$\operatorname{SL}$
-oriented theory. Since
![]() ${\mathcal{W}}={\mathcal{K}}_{\ast }^{MW}[\unicode[STIX]{x1D702}^{-1}]$
, the Eilenberg–MacLane spectrum
${\mathcal{W}}={\mathcal{K}}_{\ast }^{MW}[\unicode[STIX]{x1D702}^{-1}]$
, the Eilenberg–MacLane spectrum
![]() $EM({\mathcal{W}})$
is
$EM({\mathcal{W}})$
is
![]() $\operatorname{SL}$
-oriented and
$\operatorname{SL}$
-oriented and
![]() $\unicode[STIX]{x1D702}$
invertible.
$\unicode[STIX]{x1D702}$
invertible.
Remark 3.2. Ananyevskiy [Reference Ananyevskiy1, Corollary 5.4.] shows, that for
![]() ${\mathcal{E}}\in \operatorname{SH}(k)$
a motivic ring spectrum such that
${\mathcal{E}}\in \operatorname{SH}(k)$
a motivic ring spectrum such that
![]() ${\mathcal{E}}^{0,0}$
is a Zariski sheaf on
${\mathcal{E}}^{0,0}$
is a Zariski sheaf on
![]() $\mathbf{Sm}/k$
,
$\mathbf{Sm}/k$
,
![]() ${\mathcal{E}}$
admits a unique
${\mathcal{E}}$
admits a unique
![]() $\operatorname{SL}$
orientation.
$\operatorname{SL}$
orientation.
We recall the following results of Ananyevskiy.
Theorem 3.3. [Reference Ananyevskiy3, Theorem 10]
For
![]() ${\mathcal{E}}$
an
${\mathcal{E}}$
an
![]() $\unicode[STIX]{x1D702}$
-invertible,
$\unicode[STIX]{x1D702}$
-invertible,
![]() $\operatorname{SL}$
-oriented theory, one has
$\operatorname{SL}$
-oriented theory, one has
Here
![]() $p_{i}=p_{i}(E_{n})$
,
$p_{i}=p_{i}(E_{n})$
,
![]() $e=e(E_{n})$
, where
$e=e(E_{n})$
, where
![]() $E_{n}\rightarrow \operatorname{BSL}_{n}$
is the universal rank
$E_{n}\rightarrow \operatorname{BSL}_{n}$
is the universal rank
![]() $n$
bundle. Moreover,
$n$
bundle. Moreover,
![]() $p_{m}(E_{2m})=e(E_{2m})^{2}$
.
$p_{m}(E_{2m})=e(E_{2m})^{2}$
.
and
Theorem 3.4. (
 $\operatorname{SL}_{2}$
-splitting principle)
$\operatorname{SL}_{2}$
-splitting principle)
Let
![]() $i_{m}:(\operatorname{SL}_{2})^{m}\rightarrow \operatorname{SL}_{2m}$
be the block-diagonal inclusion and let
$i_{m}:(\operatorname{SL}_{2})^{m}\rightarrow \operatorname{SL}_{2m}$
be the block-diagonal inclusion and let
![]() ${\mathcal{E}}$
be an
${\mathcal{E}}$
be an
![]() $\unicode[STIX]{x1D702}$
-invertible,
$\unicode[STIX]{x1D702}$
-invertible,
![]() $\operatorname{SL}$
-oriented theory. Then
$\operatorname{SL}$
-oriented theory. Then
is injective. Moreover,
where
![]() $e_{i}$
is the pullback of
$e_{i}$
is the pullback of
![]() $e\in {\mathcal{E}}^{2,1}(\operatorname{BSL}_{2})$
via the
$e\in {\mathcal{E}}^{2,1}(\operatorname{BSL}_{2})$
via the
![]() $i$
th projection, and
$i$
th projection, and
This latter result is a consequence of [Reference Ananyevskiy3, Theorems 6, 10].
4
 $\operatorname{BGL}_{n}$
and
$\operatorname{BGL}_{n}$
and
 $\operatorname{BSL}_{n}$
$\operatorname{BSL}_{n}$
Let
![]() $\unicode[STIX]{x1D70B}_{n}:\operatorname{BSL}_{n}\rightarrow \operatorname{BGL}_{n}$
be the canonical map,
$\unicode[STIX]{x1D70B}_{n}:\operatorname{BSL}_{n}\rightarrow \operatorname{BGL}_{n}$
be the canonical map,
![]() $E_{n}\rightarrow \operatorname{BGL}_{n}$
the universal rank
$E_{n}\rightarrow \operatorname{BGL}_{n}$
the universal rank
![]() $n$
vector bundle. For
$n$
vector bundle. For
![]() ${\mathcal{E}}$
an
${\mathcal{E}}$
an
![]() $\operatorname{SL}$
-oriented motivic ring spectrum, we have the pullback map
$\operatorname{SL}$
-oriented motivic ring spectrum, we have the pullback map
In addition, the bundle
![]() $\unicode[STIX]{x1D70B}^{\ast }E_{n}$
is canonically isomorphic to the universal bundle
$\unicode[STIX]{x1D70B}^{\ast }E_{n}$
is canonically isomorphic to the universal bundle
![]() $\tilde{E}_{n}\rightarrow \operatorname{BSL}_{n}$
, hence there is a canonical trivialization
$\tilde{E}_{n}\rightarrow \operatorname{BSL}_{n}$
, hence there is a canonical trivialization
![]() $\unicode[STIX]{x1D703}:\unicode[STIX]{x1D70B}^{\ast }\operatorname{det}^{-1}E_{n}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\operatorname{BSL}_{n}}$
. We may therefore define
$\unicode[STIX]{x1D703}:\unicode[STIX]{x1D70B}^{\ast }\operatorname{det}^{-1}E_{n}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\operatorname{BSL}_{n}}$
. We may therefore define
as the composition
Our main theorem of this section is
Theorem 4.1. Let
![]() ${\mathcal{E}}\in \operatorname{SH}(k)$
be an
${\mathcal{E}}\in \operatorname{SH}(k)$
be an
![]() $\operatorname{SL}$
-oriented,
$\operatorname{SL}$
-oriented,
![]() $\unicode[STIX]{x1D702}$
-invertible motivic ring spectrum. Suppose that either
$\unicode[STIX]{x1D702}$
-invertible motivic ring spectrum. Suppose that either
![]() ${\mathcal{E}}^{0,0}$
is a Zariski sheaf on
${\mathcal{E}}^{0,0}$
is a Zariski sheaf on
![]() $\mathbf{Sm}/k$
or, that the unit map
$\mathbf{Sm}/k$
or, that the unit map
![]() $\mathbb{S}_{k}\rightarrow {\mathcal{E}}$
makes
$\mathbb{S}_{k}\rightarrow {\mathcal{E}}$
makes
![]() ${\mathcal{E}}^{0,0}$
a
${\mathcal{E}}^{0,0}$
a
![]() ${\mathcal{W}}$
-module. Then for
${\mathcal{W}}$
-module. Then for
![]() $n=2m$
,
$n=2m$
,
![]() $\unicode[STIX]{x1D70B}^{\ast }$
induces an isomorphism
$\unicode[STIX]{x1D70B}^{\ast }$
induces an isomorphism
More precisely,
For
![]() $n=2m+1$
,
$n=2m+1$
,
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};\operatorname{det}E_{n})\!)=0$
and
${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};\operatorname{det}E_{n})\!)=0$
and
is an isomorphism.
Proof. Write
![]() $\bar{\unicode[STIX]{x1D70B}}:L\rightarrow \operatorname{BGL}_{n}$
for the line bundle
$\bar{\unicode[STIX]{x1D70B}}:L\rightarrow \operatorname{BGL}_{n}$
for the line bundle
![]() $\operatorname{det}E_{n}$
. We may identify the morphism
$\operatorname{det}E_{n}$
. We may identify the morphism
![]() $\unicode[STIX]{x1D70B}:\operatorname{BSL}_{n}\rightarrow \operatorname{BGL}_{n}$
with the principal
$\unicode[STIX]{x1D70B}:\operatorname{BSL}_{n}\rightarrow \operatorname{BGL}_{n}$
with the principal
![]() $\mathbb{G}_{m}$
-bundle
$\mathbb{G}_{m}$
-bundle
![]() $L-0_{L}$
associated to
$L-0_{L}$
associated to
![]() $L\rightarrow \operatorname{BGL}_{n}$
. Identifying
$L\rightarrow \operatorname{BGL}_{n}$
. Identifying
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n})$
with
${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n})$
with
![]() ${\mathcal{E}}^{\ast \ast }(L)$
via
${\mathcal{E}}^{\ast \ast }(L)$
via
![]() $\bar{\unicode[STIX]{x1D70B}}^{\ast }$
and using homotopy invariance gives us the localization sequences
$\bar{\unicode[STIX]{x1D70B}}^{\ast }$
and using homotopy invariance gives us the localization sequences
 $$\begin{eqnarray}\displaystyle \cdots \rightarrow {\mathcal{E}}^{a,b}(\operatorname{BGL}_{n}) & \xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }} & \displaystyle {\mathcal{E}}^{a,b}(\operatorname{BSL}_{n})\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{E}}^{a-1,b-1}(\operatorname{BGL}_{n};L)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{a-1}}{\mathcal{E}}^{a+1,b}(\operatorname{BGL}_{n})\rightarrow \cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \cdots \rightarrow {\mathcal{E}}^{a,b}(\operatorname{BGL}_{n}) & \xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }} & \displaystyle {\mathcal{E}}^{a,b}(\operatorname{BSL}_{n})\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{E}}^{a-1,b-1}(\operatorname{BGL}_{n};L)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{a-1}}{\mathcal{E}}^{a+1,b}(\operatorname{BGL}_{n})\rightarrow \cdots \nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}_{a-1}$
is cup product with the Euler class
$\unicode[STIX]{x1D719}_{a-1}$
is cup product with the Euler class
![]() $e(L)$
.
$e(L)$
.
By Lemma 4.3 or [Reference Ananyevskiy2, Theorem 2(Ia)],
![]() $e(L)=0$
and thus the localization sequence splits into short exact sequences
$e(L)=0$
and thus the localization sequence splits into short exact sequences
Next, we define a splitting to
![]() $\unicode[STIX]{x2202}_{a,b}$
. Let
$\unicode[STIX]{x2202}_{a,b}$
. Let
![]() $t\in H^{0}(L,\bar{\unicode[STIX]{x1D70B}}^{\ast }L)$
be the tautological section, giving a generator of
$t\in H^{0}(L,\bar{\unicode[STIX]{x1D70B}}^{\ast }L)$
be the tautological section, giving a generator of
![]() $\bar{\unicode[STIX]{x1D70B}}^{\ast }L$
over
$\bar{\unicode[STIX]{x1D70B}}^{\ast }L$
over
![]() $L-0_{L}$
. Let
$L-0_{L}$
. Let
![]() $t^{\vee }\in H^{0}(L-0_{L},\bar{\unicode[STIX]{x1D70B}}^{\ast }L^{-1})$
be the dual of
$t^{\vee }\in H^{0}(L-0_{L},\bar{\unicode[STIX]{x1D70B}}^{\ast }L^{-1})$
be the dual of
![]() $t$
. This defines the
$t$
. This defines the
![]() $\bar{\unicode[STIX]{x1D70B}}^{\ast }L^{-1}$
-valued quadratic form
$\bar{\unicode[STIX]{x1D70B}}^{\ast }L^{-1}$
-valued quadratic form
![]() $q(s)=s^{2}\cdot t^{\vee }$
, giving the section
$q(s)=s^{2}\cdot t^{\vee }$
, giving the section
![]() $\langle t^{\vee }\rangle$
of the sheaf of twisted Witt groups
$\langle t^{\vee }\rangle$
of the sheaf of twisted Witt groups
![]() $W(L^{-1})$
over
$W(L^{-1})$
over
![]() $L-\{0_{L}\}$
.
$L-\{0_{L}\}$
.
Suppose the unit map
![]() $\mathbb{S}_{k}\rightarrow {\mathcal{E}}$
makes
$\mathbb{S}_{k}\rightarrow {\mathcal{E}}$
makes
![]() ${\mathcal{E}}^{\ast \ast }(-)$
into a
${\mathcal{E}}^{\ast \ast }(-)$
into a
![]() ${\mathcal{W}}(-)$
module. This gives us the section
${\mathcal{W}}(-)$
module. This gives us the section
![]() $\langle t^{\vee }\rangle _{{\mathcal{E}}}:=\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}\in {\mathcal{E}}^{0,0}(L-\{0_{\operatorname{BGL}_{n}}\};L^{-1})$
, that is
$\langle t^{\vee }\rangle _{{\mathcal{E}}}:=\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}\in {\mathcal{E}}^{0,0}(L-\{0_{\operatorname{BGL}_{n}}\};L^{-1})$
, that is
![]() $\langle t^{\vee }\rangle _{{\mathcal{E}}}\in {\mathcal{E}}^{0,0}(\operatorname{BSL}_{n},L^{-1})$
. One finds
$\langle t^{\vee }\rangle _{{\mathcal{E}}}\in {\mathcal{E}}^{0,0}(\operatorname{BSL}_{n},L^{-1})$
. One finds
by making a computation in local coordinates. Indeed, we may first make the computation for
![]() ${\mathcal{E}}=\operatorname{EM}({\mathcal{W}})$
,
${\mathcal{E}}=\operatorname{EM}({\mathcal{W}})$
,
![]() $\operatorname{EM}({\mathcal{W}})^{a,b}(-)=H^{a-b}(-,{\mathcal{W}})$
, in which case
$\operatorname{EM}({\mathcal{W}})^{a,b}(-)=H^{a-b}(-,{\mathcal{W}})$
, in which case
![]() ${\mathcal{E}}^{-1,-1}(-)=H^{0}(-,{\mathcal{W}})$
, justifying the local computation. In general, we have
${\mathcal{E}}^{-1,-1}(-)=H^{0}(-,{\mathcal{W}})$
, justifying the local computation. In general, we have
![]() $\langle t^{\vee }\rangle _{{\mathcal{E}}}=\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}$
and so
$\langle t^{\vee }\rangle _{{\mathcal{E}}}=\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}$
and so
![]() $\unicode[STIX]{x2202}\langle t^{\vee }\rangle _{{\mathcal{E}}}=\unicode[STIX]{x2202}\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}=\unicode[STIX]{x1D702}\cdot 1_{{\mathcal{E}}}$
. In addition, the map
$\unicode[STIX]{x2202}\langle t^{\vee }\rangle _{{\mathcal{E}}}=\unicode[STIX]{x2202}\langle t^{\vee }\rangle \cdot 1_{{\mathcal{E}}}=\unicode[STIX]{x1D702}\cdot 1_{{\mathcal{E}}}$
. In addition, the map
is equal to the composition
which one sees by noting that multiplication by
![]() $t^{\vee }$
is the same as the canonical trivialization
$t^{\vee }$
is the same as the canonical trivialization
![]() $\unicode[STIX]{x1D70B}^{\ast }L\rightarrow {\mathcal{O}}_{\operatorname{BSL}_{n}}$
. Thus
$\unicode[STIX]{x1D70B}^{\ast }L\rightarrow {\mathcal{O}}_{\operatorname{BSL}_{n}}$
. Thus
which is an isomorphism, since
![]() ${\mathcal{E}}$
is an
${\mathcal{E}}$
is an
![]() $\unicode[STIX]{x1D702}$
-invertible theory.
$\unicode[STIX]{x1D702}$
-invertible theory.
In case
![]() ${\mathcal{E}}^{0,0}$
is a Zariski sheaf, as
${\mathcal{E}}^{0,0}$
is a Zariski sheaf, as
![]() ${\mathcal{E}}$
is
${\mathcal{E}}$
is
![]() $\unicode[STIX]{x1D702}$
-invertible,
$\unicode[STIX]{x1D702}$
-invertible,
![]() ${\mathcal{E}}^{-1,-1}$
is also a Zariski sheaf, so the computation of
${\mathcal{E}}^{-1,-1}$
is also a Zariski sheaf, so the computation of
![]() $\unicode[STIX]{x2202}\langle t^{\vee }\rangle _{{\mathcal{E}}}$
may be made locally as above, with the same result.
$\unicode[STIX]{x2202}\langle t^{\vee }\rangle _{{\mathcal{E}}}$
may be made locally as above, with the same result.
It remains to compute the image of the two summands. For
![]() $n=2m+1$
, the map
$n=2m+1$
, the map
is surjective: since the Pontryagin classes are defined for arbitrary vector bundles, and are functorial, we have
The surjectivity then follows from Ananyevskiy’s description of
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
, and this implies that the remaining summand
${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
, and this implies that the remaining summand
![]() ${\mathcal{E}}^{\ast ,\ast }(\operatorname{BGL}_{n};L)$
must be zero.
${\mathcal{E}}^{\ast ,\ast }(\operatorname{BGL}_{n};L)$
must be zero.
Now take
![]() $n=2m$
. We write
$n=2m$
. We write
![]() $R_{m-1}$
for the subring
$R_{m-1}$
for the subring
![]() ${\mathcal{E}}^{\ast \ast }(k)[p_{1},\ldots ,p_{m-1}]$
of
${\mathcal{E}}^{\ast \ast }(k)[p_{1},\ldots ,p_{m-1}]$
of
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
. The same argument as above together with the identity
${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
. The same argument as above together with the identity
implies that
![]() $\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n}))$
contains
$\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n}))$
contains
![]() $R_{m-1}[e^{2}]$
, and
$R_{m-1}[e^{2}]$
, and
![]() $e$
is in
$e$
is in
![]() $\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L))$
. Since
$\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L))$
. Since
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L)$
is a module for
${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L)$
is a module for
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n})$
, this shows that the
${\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n})$
, this shows that the
![]() $R_{m-1}[e^{2}]$
-submodule
$R_{m-1}[e^{2}]$
-submodule
![]() $e\cdot R_{m-1}[e^{2}]$
of
$e\cdot R_{m-1}[e^{2}]$
of
![]() ${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
is contained in
${\mathcal{E}}^{\ast \ast }(\operatorname{BSL}_{n})$
is contained in
![]() $\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L))$
. Since
$\unicode[STIX]{x1D70B}_{n}^{\ast }({\mathcal{E}}^{\ast \ast }(\operatorname{BGL}_{n};L))$
. Since
the result for
![]() $n=2m$
follows.
$n=2m$
follows.
Remark 4.2. Since the Eilenberg–MacLane spectrum
![]() $\operatorname{EM}({\mathcal{W}})$
is
$\operatorname{EM}({\mathcal{W}})$
is
![]() $\operatorname{SL}$
-oriented and
$\operatorname{SL}$
-oriented and
![]() $\unicode[STIX]{x1D702}$
invertible we may apply Theorem 4.1 to give a computation of
$\unicode[STIX]{x1D702}$
invertible we may apply Theorem 4.1 to give a computation of
![]() $H^{\ast }(\operatorname{BGL}_{n},{\mathcal{W}})$
and
$H^{\ast }(\operatorname{BGL}_{n},{\mathcal{W}})$
and
![]() $H^{\ast }(\operatorname{BGL}_{n},{\mathcal{W}}(\operatorname{det}E_{n}))$
: for
$H^{\ast }(\operatorname{BGL}_{n},{\mathcal{W}}(\operatorname{det}E_{n}))$
: for
![]() $n=2m$
,
$n=2m$
,
and for
![]() $n=2m+1$
,
$n=2m+1$
,
We used the following result, a slight extension of a result of Ananyevskiy’s [Reference Ananyevskiy1, Theorem 7.4], in the proof of Theorem 4.1.
Lemma 4.3. Let
![]() ${\mathcal{E}}\in \operatorname{SH}(k)$
be an
${\mathcal{E}}\in \operatorname{SH}(k)$
be an
![]() $\operatorname{SL}$
-oriented,
$\operatorname{SL}$
-oriented,
![]() $\unicode[STIX]{x1D702}$
-invertible motivic ring spectrum. Then for
$\unicode[STIX]{x1D702}$
-invertible motivic ring spectrum. Then for
![]() $X\in \mathbf{Sm}/k$
and
$X\in \mathbf{Sm}/k$
and
![]() $V\rightarrow X$
a vector bundle of odd rank
$V\rightarrow X$
a vector bundle of odd rank
![]() $r$
, we have
$r$
, we have
![]() $e(V)=0$
in
$e(V)=0$
in
![]() ${\mathcal{E}}^{2r,r}(X;\operatorname{det}V^{-1})$
.
${\mathcal{E}}^{2r,r}(X;\operatorname{det}V^{-1})$
.
Proof. Let
![]() $L=\operatorname{det}^{-1}V$
. By definition,
$L=\operatorname{det}^{-1}V$
. By definition,
![]() ${\mathcal{E}}^{2r,r}(X;L)={\mathcal{E}}_{0_{L}}^{2r+2,r+1}(L)$
. We have the canonical trivialization
${\mathcal{E}}^{2r,r}(X;L)={\mathcal{E}}_{0_{L}}^{2r+2,r+1}(L)$
. We have the canonical trivialization
![]() $\unicode[STIX]{x1D706}:\operatorname{det}(V\oplus L)\rightarrow {\mathcal{O}}_{X}$
, giving the Thom class
$\unicode[STIX]{x1D706}:\operatorname{det}(V\oplus L)\rightarrow {\mathcal{O}}_{X}$
, giving the Thom class
![]() $\operatorname{th}(V\oplus L,\unicode[STIX]{x1D706})\in {\mathcal{E}}_{0_{V}\times 0_{L}}^{2r+2,r+1}(V\oplus L)$
, and the Euler class
$\operatorname{th}(V\oplus L,\unicode[STIX]{x1D706})\in {\mathcal{E}}_{0_{V}\times 0_{L}}^{2r+2,r+1}(V\oplus L)$
, and the Euler class
![]() $e(V)\in {\mathcal{E}}^{2r,r}(X;L)$
is by definition the pullback
$e(V)\in {\mathcal{E}}^{2r,r}(X;L)$
is by definition the pullback
![]() $s_{0_{V}}^{\ast }(\operatorname{th}(V\oplus L,\unicode[STIX]{x1D706}))\in {\mathcal{E}}_{0_{L}}^{2r+2,r+1}(L)$
, where
$s_{0_{V}}^{\ast }(\operatorname{th}(V\oplus L,\unicode[STIX]{x1D706}))\in {\mathcal{E}}_{0_{L}}^{2r+2,r+1}(L)$
, where
![]() $s_{0_{V}}:L\rightarrow V\oplus L$
is the closed immersion
$s_{0_{V}}:L\rightarrow V\oplus L$
is the closed immersion
![]() $s_{0_{V}}(x)=(0_{V},x)$
.
$s_{0_{V}}(x)=(0_{V},x)$
.
Let
![]() $\unicode[STIX]{x1D70B}:X\times \mathbb{A}^{1}-\{0\}\rightarrow X$
be the projection, let
$\unicode[STIX]{x1D70B}:X\times \mathbb{A}^{1}-\{0\}\rightarrow X$
be the projection, let
![]() $t$
be the standard unit on
$t$
be the standard unit on
![]() $\mathbb{A}^{1}-\{0\}$
and let
$\mathbb{A}^{1}-\{0\}$
and let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}^{\ast }(V\oplus L)\rightarrow \unicode[STIX]{x1D70B}^{\ast }(V\oplus L)$
be the automorphism
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}^{\ast }(V\oplus L)\rightarrow \unicode[STIX]{x1D70B}^{\ast }(V\oplus L)$
be the automorphism
![]() $t\cdot \text{Id}_{\unicode[STIX]{x1D70B}^{\ast }V}\oplus \text{Id}_{\unicode[STIX]{x1D70B}^{\ast }L}$
. We also use
$t\cdot \text{Id}_{\unicode[STIX]{x1D70B}^{\ast }V}\oplus \text{Id}_{\unicode[STIX]{x1D70B}^{\ast }L}$
. We also use
![]() $\unicode[STIX]{x1D70B}$
to denote the induced projections
$\unicode[STIX]{x1D70B}$
to denote the induced projections
![]() $\unicode[STIX]{x1D70B}^{\ast }V\rightarrow V$
,
$\unicode[STIX]{x1D70B}^{\ast }V\rightarrow V$
,
![]() $\unicode[STIX]{x1D70B}^{\ast }L\rightarrow L$
, and so on, and let
$\unicode[STIX]{x1D70B}^{\ast }L\rightarrow L$
, and so on, and let
![]() $\unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}:\unicode[STIX]{x1D70B}^{\ast }L\rightarrow \unicode[STIX]{x1D70B}^{\ast }(V\oplus L)$
denote the map induced by
$\unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}:\unicode[STIX]{x1D70B}^{\ast }L\rightarrow \unicode[STIX]{x1D70B}^{\ast }(V\oplus L)$
denote the map induced by
![]() $s_{0_{V}}$
. The proof of [Reference Ananyevskiy1, Theorem 7.4] gives the identity
$s_{0_{V}}$
. The proof of [Reference Ananyevskiy1, Theorem 7.4] gives the identity
and since
![]() $\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}=\unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}$
, this implies
$\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}=\unicode[STIX]{x1D70B}^{\ast }s_{0_{V}}$
, this implies
Following Ananyevskiy’s argument (where the minus sign disappears since we are using the “alternate” normalization mentioned in [Reference Ananyevskiy1, Remark 6.5]), applying the boundary in the localization sequence
gives the identity
in
![]() ${\mathcal{E}}^{2r-1,r-1}(X;\operatorname{det}^{-1}V)$
. Since
${\mathcal{E}}^{2r-1,r-1}(X;\operatorname{det}^{-1}V)$
. Since
![]() ${\mathcal{E}}$
is by assumption an
${\mathcal{E}}$
is by assumption an
![]() $\unicode[STIX]{x1D702}$
-invertible theory, we have
$\unicode[STIX]{x1D702}$
-invertible theory, we have
![]() $e(V)=0$
.
$e(V)=0$
.
5 Witt cohomology of
 $BN_{T}(\operatorname{SL}_{2})$
$BN_{T}(\operatorname{SL}_{2})$
In this section, for
![]() $V\rightarrow X$
a vector bundle, we let
$V\rightarrow X$
a vector bundle, we let
![]() $f:\mathbb{P}(V)\rightarrow X$
denote the associated projective space bundle
$f:\mathbb{P}(V)\rightarrow X$
denote the associated projective space bundle
![]() $\operatorname{Proj}_{{\mathcal{O}}_{X}}(\operatorname{Sym}^{\ast }V^{\vee })$
. We have the tautological subbundle
$\operatorname{Proj}_{{\mathcal{O}}_{X}}(\operatorname{Sym}^{\ast }V^{\vee })$
. We have the tautological subbundle
![]() $O(-1)\rightarrow \mathbb{P}(V)$
of
$O(-1)\rightarrow \mathbb{P}(V)$
of
![]() $f^{\ast }V$
and its dual
$f^{\ast }V$
and its dual
![]() $O(1)$
.
$O(1)$
.
We have the
![]() $\operatorname{SL}$
-oriented theory
$\operatorname{SL}$
-oriented theory
![]() $\operatorname{EM}({\mathcal{W}})^{a,b}(X):=H^{a-b}(X,{\mathcal{W}})$
on
$\operatorname{EM}({\mathcal{W}})^{a,b}(X):=H^{a-b}(X,{\mathcal{W}})$
on
![]() $\mathbf{Sm}/k$
, where
$\mathbf{Sm}/k$
, where
![]() ${\mathcal{W}}$
is the sheaf of Witt rings. Our main goal in this section is to compute
${\mathcal{W}}$
is the sheaf of Witt rings. Our main goal in this section is to compute
![]() $H^{\ast }(BN_{T}(\operatorname{SL}_{2}),{\mathcal{W}})$
, where
$H^{\ast }(BN_{T}(\operatorname{SL}_{2}),{\mathcal{W}})$
, where
![]() $N_{T}(\operatorname{SL}_{2})\subset \operatorname{SL}_{2}$
is the normalizer of the standard torus
$N_{T}(\operatorname{SL}_{2})\subset \operatorname{SL}_{2}$
is the normalizer of the standard torus
We write
![]() $N:=N_{T}(\operatorname{SL}_{2})$
.
$N:=N_{T}(\operatorname{SL}_{2})$
.
![]() $N$
is generated by
$N$
is generated by
![]() $T$
and an additional element
$T$
and an additional element
![]() $\unicode[STIX]{x1D70E}=(\!\begin{smallmatrix}0 & 1\\ -1 & 0\end{smallmatrix}\!)$
, and sending
$\unicode[STIX]{x1D70E}=(\!\begin{smallmatrix}0 & 1\\ -1 & 0\end{smallmatrix}\!)$
, and sending
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
![]() $-1$
gives us the exact sequence
$-1$
gives us the exact sequence
This gives us the representation
![]() $\unicode[STIX]{x1D70C}^{-}:N\rightarrow \mathbb{G}_{m}$
sending
$\unicode[STIX]{x1D70C}^{-}:N\rightarrow \mathbb{G}_{m}$
sending
![]() $T$
to
$T$
to
![]() $1$
and
$1$
and
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
![]() $-1$
(see §6 below).
$-1$
(see §6 below).
We work over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
. In this case, the computation of Section 2 gives the isomorphism
$\neq 2$
. In this case, the computation of Section 2 gives the isomorphism
with
![]() $C$
the conic defined by
$C$
the conic defined by
![]() $Q:=T_{1}^{2}-4T_{0}T_{2}$
.
$Q:=T_{1}^{2}-4T_{0}T_{2}$
.
The natural right
![]() $\operatorname{SL}_{2}$
-action on
$\operatorname{SL}_{2}$
-action on
![]() $N\backslash \operatorname{SL}_{2}$
can be described in the model
$N\backslash \operatorname{SL}_{2}$
can be described in the model
![]() $\mathbb{P}^{2}-C$
as follows. Let
$\mathbb{P}^{2}-C$
as follows. Let
![]() $F=\mathbb{A}^{2}$
with the standard (right)
$F=\mathbb{A}^{2}$
with the standard (right)
![]() $\operatorname{SL}_{2}$
-action. We have the canonical map of schemes
$\operatorname{SL}_{2}$
-action. We have the canonical map of schemes
induced by the squaring map
![]() $sq:F\rightarrow \operatorname{Sym}^{2}F$
, where
$sq:F\rightarrow \operatorname{Sym}^{2}F$
, where
![]() $sq(v)$
is the image of
$sq(v)$
is the image of
![]() $v\otimes v$
under the canonical surjection
$v\otimes v$
under the canonical surjection
![]() $F\otimes F\rightarrow \operatorname{Sym}^{2}F$
. As the right
$F\otimes F\rightarrow \operatorname{Sym}^{2}F$
. As the right
![]() $\operatorname{SL}_{2}$
-action on
$\operatorname{SL}_{2}$
-action on
![]() $\operatorname{Sym}^{2}F$
is induced by the diagonal action on
$\operatorname{Sym}^{2}F$
is induced by the diagonal action on
![]() $F\otimes F$
,
$F\otimes F$
,
![]() $(v\otimes w)\cdot g:=v\cdot g\otimes w\cdot g$
, the map
$(v\otimes w)\cdot g:=v\cdot g\otimes w\cdot g$
, the map
![]() $sq$
is
$sq$
is
![]() $\operatorname{SL}_{2}$
-equivariant.
$\operatorname{SL}_{2}$
-equivariant.
This identifies
![]() $C\subset \mathbb{P}^{2}$
with
$C\subset \mathbb{P}^{2}$
with
![]() $sq((\mathbb{P}(F))\subset \mathbb{P}(\operatorname{Sym}^{2}F)$
. Furthermore, the quadratic polynomial
$sq((\mathbb{P}(F))\subset \mathbb{P}(\operatorname{Sym}^{2}F)$
. Furthermore, the quadratic polynomial
![]() $Q=T_{1}^{2}-4T_{0}T_{2}$
gives us a global section
$Q=T_{1}^{2}-4T_{0}T_{2}$
gives us a global section
![]() $\langle Q\rangle$
of
$\langle Q\rangle$
of
![]() ${\mathcal{O}}_{\mathbb{P}^{2}-C}^{\times }/{\mathcal{O}}_{\mathbb{P}^{2}-C}^{\times ~2}$
, with value
${\mathcal{O}}_{\mathbb{P}^{2}-C}^{\times }/{\mathcal{O}}_{\mathbb{P}^{2}-C}^{\times ~2}$
, with value
![]() $Q/L^{2}$
on
$Q/L^{2}$
on
![]() $\mathbb{P}^{2}-(C\cup \{L=0\})$
for each linear form
$\mathbb{P}^{2}-(C\cup \{L=0\})$
for each linear form
![]() $L$
. As the map sending a unit
$L$
. As the map sending a unit
![]() $u$
to the class of the rank one quadratric form
$u$
to the class of the rank one quadratric form
![]() $\langle u\rangle$
descends to a map of sheaves
$\langle u\rangle$
descends to a map of sheaves
![]() ${\mathcal{O}}^{\times }/{\mathcal{O}}^{\times 2}\rightarrow {\mathcal{G}}{\mathcal{W}}^{\times }$
, we have the section
${\mathcal{O}}^{\times }/{\mathcal{O}}^{\times 2}\rightarrow {\mathcal{G}}{\mathcal{W}}^{\times }$
, we have the section
![]() $\langle q\rangle$
of
$\langle q\rangle$
of
![]() ${\mathcal{G}}{\mathcal{W}}$
on
${\mathcal{G}}{\mathcal{W}}$
on
![]() $\mathbb{P}^{2}-C$
corresponding to
$\mathbb{P}^{2}-C$
corresponding to
![]() $\langle Q\rangle$
.
$\langle Q\rangle$
.
Since
![]() $C$
is stable under the
$C$
is stable under the
![]() $\operatorname{SL}_{2}$
action, the form
$\operatorname{SL}_{2}$
action, the form
![]() $Q$
is
$Q$
is
![]() $\operatorname{SL}_{2}$
invariant up to a scalar, but as
$\operatorname{SL}_{2}$
invariant up to a scalar, but as
defines a character of
![]() $\operatorname{SL}_{2}$
,
$\operatorname{SL}_{2}$
,
![]() $Q$
is
$Q$
is
![]() $\operatorname{SL}_{2}$
invariant and thus
$\operatorname{SL}_{2}$
invariant and thus
![]() $\langle Q\rangle \in H^{0}(\mathbb{P}^{2}-C,{\mathcal{O}}^{\times }/{\mathcal{O}}^{\times 2})$
is also
$\langle Q\rangle \in H^{0}(\mathbb{P}^{2}-C,{\mathcal{O}}^{\times }/{\mathcal{O}}^{\times 2})$
is also
![]() $\operatorname{SL}_{2}$
invariant.
$\operatorname{SL}_{2}$
invariant.
We may use the model
for
![]() $BN$
. The
$BN$
. The
![]() $\operatorname{SL}_{2}$
-invariant section
$\operatorname{SL}_{2}$
-invariant section
![]() $\langle Q\rangle$
of
$\langle Q\rangle$
of
![]() ${\mathcal{O}}_{N\backslash \operatorname{SL}_{2}}^{\times }/{\mathcal{O}}_{N\backslash \operatorname{SL}_{2}}^{\times ~2}$
on
${\mathcal{O}}_{N\backslash \operatorname{SL}_{2}}^{\times }/{\mathcal{O}}_{N\backslash \operatorname{SL}_{2}}^{\times ~2}$
on
![]() $N\backslash \operatorname{SL}_{2}$
thus descends to a global section
$N\backslash \operatorname{SL}_{2}$
thus descends to a global section
![]() $\langle \bar{Q}\rangle$
of
$\langle \bar{Q}\rangle$
of
![]() ${\mathcal{O}}^{\times }/{\mathcal{O}}^{\times ~2}$
on
${\mathcal{O}}^{\times }/{\mathcal{O}}^{\times ~2}$
on
![]() $BN$
, which gives us the global section
$BN$
, which gives us the global section
![]() $\langle \bar{q}\rangle$
of the sheaf of Grothendieck–Witt rings
$\langle \bar{q}\rangle$
of the sheaf of Grothendieck–Witt rings
![]() ${\mathcal{G}}{\mathcal{W}}$
on
${\mathcal{G}}{\mathcal{W}}$
on
![]() $BN$
. We also denote the image of
$BN$
. We also denote the image of
![]() $\langle \bar{q}\rangle$
in
$\langle \bar{q}\rangle$
in
![]() $H^{0}(BN,{\mathcal{W}})$
by
$H^{0}(BN,{\mathcal{W}})$
by
![]() $\langle \bar{q}\rangle$
, using the context to make the meaning clear.
$\langle \bar{q}\rangle$
, using the context to make the meaning clear.
Since
![]() $\operatorname{SL}_{2}$
is special, the bundle
$\operatorname{SL}_{2}$
is special, the bundle
![]() $E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
is Zariski locally trivial, and thus the same holds for
$E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
is Zariski locally trivial, and thus the same holds for
![]() $BN\rightarrow \operatorname{BSL}_{2}$
, as explained in Section 2.
$BN\rightarrow \operatorname{BSL}_{2}$
, as explained in Section 2.
Our description of
![]() $N\backslash \operatorname{SL}_{2}$
as
$N\backslash \operatorname{SL}_{2}$
as
![]() $\mathbb{P}(\operatorname{Sym}^{2}F)-sq(\mathbb{P}(F))$
realizes
$\mathbb{P}(\operatorname{Sym}^{2}F)-sq(\mathbb{P}(F))$
realizes
![]() $BN$
as an open subscheme of the
$BN$
as an open subscheme of the
![]() $\mathbb{P}^{2}$
-bundle
$\mathbb{P}^{2}$
-bundle
![]() $\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
with complement the
$\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
with complement the
![]() $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
![]() $\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
:
$\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
:
The representation
![]() $\unicode[STIX]{x1D70C}^{-}:N\rightarrow \mathbb{G}_{m}$
gives us the line bundle
$\unicode[STIX]{x1D70C}^{-}:N\rightarrow \mathbb{G}_{m}$
gives us the line bundle
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $BN$
, generating
$BN$
, generating
![]() $\text{Pic}(BN)$
. We have
$\text{Pic}(BN)$
. We have
![]() $\text{Pic}(N\backslash \operatorname{SL}_{2})=\mathbb{Z}/2$
with generator the restriction of
$\text{Pic}(N\backslash \operatorname{SL}_{2})=\mathbb{Z}/2$
with generator the restriction of
![]() $O_{\mathbb{P}^{2}}(1)$
, and
$O_{\mathbb{P}^{2}}(1)$
, and
![]() $\unicode[STIX]{x1D6FE}$
is the same as the bundle induced by the restriction of
$\unicode[STIX]{x1D6FE}$
is the same as the bundle induced by the restriction of
![]() $p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)$
via the canonical
$p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)$
via the canonical
![]() $\operatorname{SL}_{2}$
-linearization of
$\operatorname{SL}_{2}$
-linearization of
![]() $O_{\mathbb{P}^{2}}(1)$
. Similarly, we have the bundle
$O_{\mathbb{P}^{2}}(1)$
. Similarly, we have the bundle
![]() $p_{1}^{\ast }O(m)$
on
$p_{1}^{\ast }O(m)$
on
![]() $\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
, induced by the canonical
$\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
, induced by the canonical
![]() $\operatorname{SL}_{2}$
-linearization of
$\operatorname{SL}_{2}$
-linearization of
![]() $O_{\mathbb{P}^{1}}(1)$
.
$O_{\mathbb{P}^{1}}(1)$
.
Lemma 5.1.
Proof. The element
![]() $\unicode[STIX]{x1D702}\in K_{-1}^{MW}(k)$
is realized in
$\unicode[STIX]{x1D702}\in K_{-1}^{MW}(k)$
is realized in
![]() $\operatorname{SH}(k)$
as the stable Hopf map, the unstable version of which is the map
$\operatorname{SH}(k)$
as the stable Hopf map, the unstable version of which is the map
![]() $\unicode[STIX]{x1D702}_{2}:\mathbb{A}^{2}-\{0\}\rightarrow \mathbb{P}^{1}$
,
$\unicode[STIX]{x1D702}_{2}:\mathbb{A}^{2}-\{0\}\rightarrow \mathbb{P}^{1}$
,
![]() $\unicode[STIX]{x1D702}_{2}(x,y)=[x:y]$
. As
$\unicode[STIX]{x1D702}_{2}(x,y)=[x:y]$
. As
![]() ${\mathcal{W}}={\mathcal{K}}_{\ast }^{MW}[\unicode[STIX]{x1D702}^{-1}]$
, the projection
${\mathcal{W}}={\mathcal{K}}_{\ast }^{MW}[\unicode[STIX]{x1D702}^{-1}]$
, the projection
induces an isomorphism
Here we give
![]() $\mathbb{A}^{2}-\{0\}$
the right
$\mathbb{A}^{2}-\{0\}$
the right
![]() $\operatorname{SL}_{2}$
-action induced from the standard right action on
$\operatorname{SL}_{2}$
-action induced from the standard right action on
![]() $\mathbb{A}^{2}=F$
.
$\mathbb{A}^{2}=F$
.
Giving
![]() $\operatorname{SL}_{2}$
the right
$\operatorname{SL}_{2}$
the right
![]() $\operatorname{SL}_{2}$
-action via right multiplication, we have the
$\operatorname{SL}_{2}$
-action via right multiplication, we have the
![]() $\operatorname{SL}_{2}$
-equivariant map
$\operatorname{SL}_{2}$
-equivariant map
making
![]() $\operatorname{SL}_{2}$
an
$\operatorname{SL}_{2}$
an
![]() $\mathbb{A}^{1}$
-bundle over
$\mathbb{A}^{1}$
-bundle over
![]() $\mathbb{A}^{2}-\{0\}$
. Thus, by homotopy invariance,
$\mathbb{A}^{2}-\{0\}$
. Thus, by homotopy invariance,
is also an isomorphism. Since
![]() $E\operatorname{SL}_{2}$
is
$E\operatorname{SL}_{2}$
is
![]() $\mathbb{A}^{1}$
-contractible, we have
$\mathbb{A}^{1}$
-contractible, we have
and the lemma is proven.
Let
![]() $T\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)$
be the tangent bundle. The
$T\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)$
be the tangent bundle. The
![]() $\operatorname{SL}_{2}$
-action on
$\operatorname{SL}_{2}$
-action on
![]() $\operatorname{Sym}^{2}F$
extends canonically to an action on
$\operatorname{Sym}^{2}F$
extends canonically to an action on
![]() $T$
over its action on
$T$
over its action on
![]() $\mathbb{P}(\operatorname{Sym}^{2}F)$
, and
$\mathbb{P}(\operatorname{Sym}^{2}F)$
, and
![]() $T\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
is the relative tangent bundle of
$T\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
is the relative tangent bundle of
![]() $\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
over
$\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
over
![]() $BN$
, which we denote by
$BN$
, which we denote by
![]() ${\mathcal{T}}$
.
${\mathcal{T}}$
.
Lemma 5.2.
(1) The map
is an isomorphism. $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }:H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})\rightarrow H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }:H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})\rightarrow H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\end{eqnarray}$$
(2)
 $H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)))$
is a free
$H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)))$
is a free
 $H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
-module with degree two generator
$H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
-module with degree two generator
 $e({\mathcal{T}})$
.
$e({\mathcal{T}})$
.
Proof. (1) We use the Leray spectral sequence
As
![]() $\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
is Zariski locally trivial, it follows that
$\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}\rightarrow \operatorname{BSL}_{2}$
is Zariski locally trivial, it follows that
![]() $\unicode[STIX]{x1D70B}^{-1}(x)\cong \mathbb{P}_{k(x)}^{2}$
for all
$\unicode[STIX]{x1D70B}^{-1}(x)\cong \mathbb{P}_{k(x)}^{2}$
for all
![]() $x\in \operatorname{BSL}_{2}$
. Fasel [Reference Fasel16, Theorem 11.7] computes
$x\in \operatorname{BSL}_{2}$
. Fasel [Reference Fasel16, Theorem 11.7] computes
![]() $H^{\ast }(\mathbb{P}_{k(x)}^{2},{\mathcal{W}})$
as
$H^{\ast }(\mathbb{P}_{k(x)}^{2},{\mathcal{W}})$
as
Feeding this into the Leray spectral sequence gives the result.
For (2), we do the same, using the Leray spectral sequence converging to
![]() $H^{p+q} (\!\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O(1))$
and the isomorphism
$H^{p+q} (\!\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O(1))$
and the isomorphism
again by [Reference Fasel16, Theorem 11.7]. The Gysin map
![]() $i_{p\ast }:H^{n-2}(\text{Spec }k(x),{\mathcal{W}})\rightarrow (\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))$
is left inverse to the pushforward
$i_{p\ast }:H^{n-2}(\text{Spec }k(x),{\mathcal{W}})\rightarrow (\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))$
is left inverse to the pushforward
![]() $\unicode[STIX]{x1D70B}_{\ast }:H^{n}(\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))\rightarrow H^{n-2}(\text{Spec }k(x),{\mathcal{W}})$
; it is not hard to see that for
$\unicode[STIX]{x1D70B}_{\ast }:H^{n}(\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))\rightarrow H^{n-2}(\text{Spec }k(x),{\mathcal{W}})$
; it is not hard to see that for
![]() $n=2$
, these are the isomorphism and its inverse, as given by Fasel’s computation. As
$n=2$
, these are the isomorphism and its inverse, as given by Fasel’s computation. As
![]() $\unicode[STIX]{x1D714}_{\mathbb{P}_{k(x)}^{2}/k(x)}=O_{\mathbb{P}^{2}}(-3)$
, we may replace
$\unicode[STIX]{x1D714}_{\mathbb{P}_{k(x)}^{2}/k(x)}=O_{\mathbb{P}^{2}}(-3)$
, we may replace
![]() ${\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}})$
with
${\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}})$
with
![]() ${\mathcal{W}}(O(1))\!)$
.
${\mathcal{W}}(O(1))\!)$
.
The motivic Euler characteristic
![]() $\unicode[STIX]{x1D712}(\mathbb{P}_{k(x)}^{2}/k(x))\in \operatorname{GW}(k(x))$
has been computed by Hoyois [Reference Hoyois18, Ex. 1.8] as
$\unicode[STIX]{x1D712}(\mathbb{P}_{k(x)}^{2}/k(x))\in \operatorname{GW}(k(x))$
has been computed by Hoyois [Reference Hoyois18, Ex. 1.8] as
![]() $2\langle 1\rangle +\langle -1\rangle$
, hence its image in
$2\langle 1\rangle +\langle -1\rangle$
, hence its image in
![]() $W(k)$
is
$W(k)$
is
![]() $\langle 1\rangle$
. We have the Gauß-Bonnet formula [Reference Levine and Raksit26, Theorem 1.5], which says that
$\langle 1\rangle$
. We have the Gauß-Bonnet formula [Reference Levine and Raksit26, Theorem 1.5], which says that
![]() $\unicode[STIX]{x1D712}(\mathbb{P}_{k(x)}^{2}/k(x))=\unicode[STIX]{x1D70B}_{\ast }(e(T_{\mathbb{P}_{k(x)}^{2}}))$
. This in turn implies that
$\unicode[STIX]{x1D712}(\mathbb{P}_{k(x)}^{2}/k(x))=\unicode[STIX]{x1D70B}_{\ast }(e(T_{\mathbb{P}_{k(x)}^{2}}))$
. This in turn implies that
![]() $e(T_{\mathbb{P}_{k(x)}^{2}})$
is a
$e(T_{\mathbb{P}_{k(x)}^{2}})$
is a
![]() $W(k)$
-generator for
$W(k)$
-generator for
![]() $H^{2}(\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))$
(one can also show this by computing the local indices associated to a section of
$H^{2}(\mathbb{P}_{k(x)}^{2},{\mathcal{W}}(\unicode[STIX]{x1D714}_{\mathbb{P}^{2}}))$
(one can also show this by computing the local indices associated to a section of
![]() $T_{\mathbb{P}^{2}}$
with isolated zeros, we leave the details of this to the reader). This shows that the Euler class of the relative tangent bundle
$T_{\mathbb{P}^{2}}$
with isolated zeros, we leave the details of this to the reader). This shows that the Euler class of the relative tangent bundle
![]() $e({\mathcal{T}})\in H^{2} (\!\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O(1))$
gives a global class restricting to the generators in the
$e({\mathcal{T}})\in H^{2} (\!\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O(1))$
gives a global class restricting to the generators in the
![]() $E_{1}$
-term, and thus gives a generator for
$E_{1}$
-term, and thus gives a generator for
![]() $H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)))$
as a free
$H^{\ast }(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}^{2}}(1)))$
as a free
![]() $H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
-module.
$H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
-module.
Recall we have the closed immersion
with open complement
Proposition 5.3.
(1) The map
 $p^{\ast }:H^{n}(\operatorname{BSL}_{2},{\mathcal{W}})\rightarrow H^{n}(BN,{\mathcal{W}})$
is an isomorphism for all
$p^{\ast }:H^{n}(\operatorname{BSL}_{2},{\mathcal{W}})\rightarrow H^{n}(BN,{\mathcal{W}})$
is an isomorphism for all
 $n>0$
. For
$n>0$
. For
 $n=0$
, we have the split exact sequencewith the splitting given by the section
$n=0$
, we have the split exact sequencewith the splitting given by the section $$\begin{eqnarray}0\rightarrow H^{0}(\operatorname{BSL}_{2},{\mathcal{W}})\xrightarrow[{}]{p^{\ast }}H^{0}(BN,{\mathcal{W}})\rightarrow W(k)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{0}(\operatorname{BSL}_{2},{\mathcal{W}})\xrightarrow[{}]{p^{\ast }}H^{0}(BN,{\mathcal{W}})\rightarrow W(k)\rightarrow 0\end{eqnarray}$$
 $\langle \bar{q}\rangle \in H^{0}(BN,{\mathcal{W}})$
. Explicitly
$\langle \bar{q}\rangle \in H^{0}(BN,{\mathcal{W}})$
. Explicitly  $$\begin{eqnarray}H^{\ast }(BN,{\mathcal{W}})=W(k)[p^{\ast }e]\oplus W(k)\cdot \langle \bar{q}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(BN,{\mathcal{W}})=W(k)[p^{\ast }e]\oplus W(k)\cdot \langle \bar{q}\rangle .\end{eqnarray}$$
(2)
 $H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is a free
$H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is a free
 $W(k)[p^{\ast }e]$
-module with generator
$W(k)[p^{\ast }e]$
-module with generator
 $j^{\ast }e({\mathcal{T}})$
.
$j^{\ast }e({\mathcal{T}})$
.
Proof. We recall Ananyevskiy’s computation of
![]() $H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
(Theorem 3.3):
$H^{\ast }(\operatorname{BSL}_{2},{\mathcal{W}})$
(Theorem 3.3):
where
![]() $e=e(E_{2})$
is the Euler class of the tautological rank two vector bundle on
$e=e(E_{2})$
is the Euler class of the tautological rank two vector bundle on
![]() $\operatorname{BSL}_{2}$
.
$\operatorname{BSL}_{2}$
.
Since
![]() $\text{Pic}(\operatorname{BSL}_{2})=\{1\}$
, it follows that
$\text{Pic}(\operatorname{BSL}_{2})=\{1\}$
, it follows that
![]() $\text{Pic}(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2})=\mathbb{Z}[{\mathcal{O}}(1)]$
, and thus the normal bundle of
$\text{Pic}(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2})=\mathbb{Z}[{\mathcal{O}}(1)]$
, and thus the normal bundle of
![]() $i$
is the bundle
$i$
is the bundle
![]() $p_{1}^{\ast }O_{\mathbb{P}(F)}(2)$
on
$p_{1}^{\ast }O_{\mathbb{P}(F)}(2)$
on
![]() $\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2} )$
. Moreover,
$\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2} )$
. Moreover,
![]() $i^{\ast }p_{1}^{\ast }O_{\mathbb{P}(\operatorname{Sym}^{2}F)}(m)=p_{1}^{\ast }O_{\mathbb{P}(F)}(2m)$
for all
$i^{\ast }p_{1}^{\ast }O_{\mathbb{P}(\operatorname{Sym}^{2}F)}(m)=p_{1}^{\ast }O_{\mathbb{P}(F)}(2m)$
for all
![]() $m$
. This gives us the localization sequence
$m$
. This gives us the localization sequence
 $$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow H^{n-1}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle \qquad \xrightarrow[{}]{i_{\ast }}H^{n}(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}(\operatorname{Sym}^{2}F)}(m)))\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \xrightarrow[{}]{j^{\ast }}H^{n}(BN,{\mathcal{W}})(\unicode[STIX]{x1D6FE}^{m})\xrightarrow[{}]{\unicode[STIX]{x1D6FF}}H^{n}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\rightarrow \cdots \,.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \rightarrow H^{n-1}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle \qquad \xrightarrow[{}]{i_{\ast }}H^{n}(\mathbb{P}(\operatorname{Sym}^{2}F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}}(p_{1}^{\ast }O_{\mathbb{P}(\operatorname{Sym}^{2}F)}(m)))\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \xrightarrow[{}]{j^{\ast }}H^{n}(BN,{\mathcal{W}})(\unicode[STIX]{x1D6FE}^{m})\xrightarrow[{}]{\unicode[STIX]{x1D6FF}}H^{n}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})\rightarrow \cdots \,.\nonumber\end{eqnarray}$$
The result for
![]() $n\geqslant 1$
and for
$n\geqslant 1$
and for
![]() $n=0$
and
$n=0$
and
![]() $m=1$
follows from this and the Lemmas 5.1 and 5.2. For
$m=1$
follows from this and the Lemmas 5.1 and 5.2. For
![]() $n=0$
and
$n=0$
and
![]() $m=0$
, one can check by looking at a single fiber
$m=0$
, one can check by looking at a single fiber
![]() $\unicode[STIX]{x1D70B}^{-1}(x)$
that
$\unicode[STIX]{x1D70B}^{-1}(x)$
that
![]() $\unicode[STIX]{x1D6FF}(\langle \bar{q}\rangle )$
is a
$\unicode[STIX]{x1D6FF}(\langle \bar{q}\rangle )$
is a
![]() $W(k)$
-generator for
$W(k)$
-generator for
![]() $H^{0}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})=W(k)$
.
$H^{0}(\mathbb{P}(F)\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2},{\mathcal{W}})=W(k)$
.
To conclude, we compute the multiplicative structure for
![]() $H^{\ast }(BN,{\mathcal{W}})$
and the
$H^{\ast }(BN,{\mathcal{W}})$
and the
![]() $H^{\ast }(BN,{\mathcal{W}})$
-module structure for
$H^{\ast }(BN,{\mathcal{W}})$
-module structure for
![]() $H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
. As the class
$H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
. As the class
![]() $\langle \bar{q}\rangle \in H^{0}(BN,{\mathcal{W}})$
is represented by a 1-dimensional form, we have
$\langle \bar{q}\rangle \in H^{0}(BN,{\mathcal{W}})$
is represented by a 1-dimensional form, we have
![]() $\langle \bar{q}\rangle ^{2}=1$
. It remains to compute
$\langle \bar{q}\rangle ^{2}=1$
. It remains to compute
![]() $\langle \bar{q}\rangle \cdot p^{\ast }e\in H^{2}(BN,{\mathcal{W}})$
and
$\langle \bar{q}\rangle \cdot p^{\ast }e\in H^{2}(BN,{\mathcal{W}})$
and
![]() $\langle \bar{q}\rangle \cdot j^{\ast }e({\mathcal{T}})\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
$\langle \bar{q}\rangle \cdot j^{\ast }e({\mathcal{T}})\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
For this, we consider the inclusion of the torus
![]() $\mathbb{G}_{m}\rightarrow N$
and the associated map of classifying spaces
$\mathbb{G}_{m}\rightarrow N$
and the associated map of classifying spaces
![]() $B\mathbb{G}_{m}\rightarrow BN$
, where we use the model
$B\mathbb{G}_{m}\rightarrow BN$
, where we use the model
![]() $(\mathbb{G}_{m}\backslash \operatorname{SL}_{2})\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
for
$(\mathbb{G}_{m}\backslash \operatorname{SL}_{2})\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
for
![]() $B\mathbb{G}_{m}$
. We recall that
$B\mathbb{G}_{m}$
. We recall that
![]() $BN=(\mathbb{P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F))\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
. The
$BN=(\mathbb{P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F))\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
. The
![]() $\operatorname{SL}_{2}$
-invariant section
$\operatorname{SL}_{2}$
-invariant section
![]() $Q$
of
$Q$
of
![]() ${\mathcal{O}}_{\mathbb{P}(\operatorname{Sym}^{2}F)}(2)$
gives us the section
${\mathcal{O}}_{\mathbb{P}(\operatorname{Sym}^{2}F)}(2)$
gives us the section
![]() $p_{1}^{\ast }Q$
of
$p_{1}^{\ast }Q$
of
![]() $p_{1}^{\ast }{\mathcal{O}}(2)$
. We claim that the corresponding double cover
$p_{1}^{\ast }{\mathcal{O}}(2)$
. We claim that the corresponding double cover
![]() $\text{Spec }_{{\mathcal{O}}_{BN}}(\sqrt{p_{1}^{\ast }Q})\rightarrow BN$
is isomorphic to
$\text{Spec }_{{\mathcal{O}}_{BN}}(\sqrt{p_{1}^{\ast }Q})\rightarrow BN$
is isomorphic to
![]() $B\mathbb{G}_{m}\rightarrow BN$
.
$B\mathbb{G}_{m}\rightarrow BN$
.
To see this, we note the isomorphism of schemes
which is an
![]() $\operatorname{SL}_{2}$
-equivariant isomorphism for the right action of
$\operatorname{SL}_{2}$
-equivariant isomorphism for the right action of
![]() $\operatorname{SL}_{2}$
on
$\operatorname{SL}_{2}$
on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
induced by the right action on
$\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
induced by the right action on
![]() $F$
. Since the cover
$F$
. Since the cover
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F)$
is isomorphic to
$\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F)$
is isomorphic to
![]() $\text{Spec }_{{\mathcal{O}}_{\mathbb{ P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F)}}(\sqrt{Q})$
, equivariantly for the right
$\text{Spec }_{{\mathcal{O}}_{\mathbb{ P}(\operatorname{Sym}^{2}F)-\mathbb{P}(F)}}(\sqrt{Q})$
, equivariantly for the right
![]() $\operatorname{SL}_{2}$
-actions, the assertion follows.
$\operatorname{SL}_{2}$
-actions, the assertion follows.
Lemma 5.4.
![]() $(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
in
$(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
in
![]() $H^{2}(BN,{\mathcal{W}})$
and
$H^{2}(BN,{\mathcal{W}})$
and
![]() $(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
in
$(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
in
![]() $H^{2} (\!BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE})$
.
$H^{2} (\!BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE})$
.
Proof. The relation
![]() $(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
implies that
$(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
implies that
![]() $(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
. Indeed, since
$(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
. Indeed, since
![]() $H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is a free
$H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is a free
![]() $W(k)[p^{\ast }e]$
-module, there is a unique element
$W(k)[p^{\ast }e]$
-module, there is a unique element
![]() $\unicode[STIX]{x1D706}\in W(k)$
with
$\unicode[STIX]{x1D706}\in W(k)$
with
![]() $(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=\unicode[STIX]{x1D706}\cdot j^{\ast }e({\mathcal{T}})$
. Then
$(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=\unicode[STIX]{x1D706}\cdot j^{\ast }e({\mathcal{T}})$
. Then
![]() $0=(1+\langle \bar{q}\rangle )\cdot p^{\ast }e\cdot j^{\ast }e({\mathcal{T}})=\unicode[STIX]{x1D706}\cdot (p^{\ast }e\cdot j^{\ast }e({\mathcal{T}}))$
, and as
$0=(1+\langle \bar{q}\rangle )\cdot p^{\ast }e\cdot j^{\ast }e({\mathcal{T}})=\unicode[STIX]{x1D706}\cdot (p^{\ast }e\cdot j^{\ast }e({\mathcal{T}}))$
, and as
![]() $p^{\ast }e\cdot j^{\ast }e({\mathcal{T}})$
is a generator for the free
$p^{\ast }e\cdot j^{\ast }e({\mathcal{T}})$
is a generator for the free
![]() $W(k)$
-module
$W(k)$
-module
![]() $H^{4} (\!BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE})$
,
$H^{4} (\!BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE})$
,
![]() $\unicode[STIX]{x1D706}=0$
. We now show that
$\unicode[STIX]{x1D706}=0$
. We now show that
![]() $(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
.
$(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
.
We have the tautological rank two bundle
![]() $E_{2}\rightarrow \operatorname{BSL}_{2}$
,
$E_{2}\rightarrow \operatorname{BSL}_{2}$
,
![]() $E_{2}:=F\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
and its pullback
$E_{2}:=F\times ^{\operatorname{SL}_{2}}E\operatorname{SL}_{2}$
and its pullback
![]() $\tilde{E}_{2}\rightarrow BN$
. The class
$\tilde{E}_{2}\rightarrow BN$
. The class
![]() $e\in H^{2}(\operatorname{BSL}_{2},{\mathcal{W}})$
is the Euler class
$e\in H^{2}(\operatorname{BSL}_{2},{\mathcal{W}})$
is the Euler class
![]() $e(E_{2})$
, so
$e(E_{2})$
, so
![]() $p^{\ast }e=e(\tilde{E}_{2})$
. We have the cover
$p^{\ast }e=e(\tilde{E}_{2})$
. We have the cover
![]() $\unicode[STIX]{x1D719}:B\mathbb{G}_{m}\rightarrow BN$
with fiber
$\unicode[STIX]{x1D719}:B\mathbb{G}_{m}\rightarrow BN$
with fiber
![]() $\mathbb{G}_{m}\backslash N=\mathbb{Z}/2$
corresponding to the inclusion
$\mathbb{G}_{m}\backslash N=\mathbb{Z}/2$
corresponding to the inclusion
![]() $\mathbb{G}_{m}\rightarrow N$
. The pullback
$\mathbb{G}_{m}\rightarrow N$
. The pullback
![]() $\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
splits as a direct sum
$\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
splits as a direct sum
corresponding to the decomposition of
![]() $F$
into the
$F$
into the
![]() $t$
and
$t$
and
![]() $t^{-1}$
eigenspaces for the torus
$t^{-1}$
eigenspaces for the torus
![]() $\mathbb{G}_{m}\subset \operatorname{SL}_{2}$
. The
$\mathbb{G}_{m}\subset \operatorname{SL}_{2}$
. The
![]() $\mathbb{Z}/2$
-action on
$\mathbb{Z}/2$
-action on
![]() $B\mathbb{G}_{m}$
corresponds to the automorphism
$B\mathbb{G}_{m}$
corresponds to the automorphism
![]() $t\mapsto t^{-1}$
of
$t\mapsto t^{-1}$
of
![]() $\mathbb{G}_{m}$
and exchanges the two factors
$\mathbb{G}_{m}$
and exchanges the two factors
![]() $O(1)$
and
$O(1)$
and
![]() $O(-1)$
. By descent, the union of the two “coordinate axes”
$O(-1)$
. By descent, the union of the two “coordinate axes”
![]() $O(1)\times 0\cup 0\times O(-1)\subset \unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
gives us the cone
$O(1)\times 0\cup 0\times O(-1)\subset \unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
gives us the cone
![]() $\mathfrak{C}\subset \tilde{E}_{2}$
, which on each geometric fiber is the union of two lines through the origin. The normalization
$\mathfrak{C}\subset \tilde{E}_{2}$
, which on each geometric fiber is the union of two lines through the origin. The normalization
![]() $\unicode[STIX]{x1D708}:\mathfrak{C}^{N}\rightarrow \mathfrak{C}$
is thus isomorphic to the total space of the bundle
$\unicode[STIX]{x1D708}:\mathfrak{C}^{N}\rightarrow \mathfrak{C}$
is thus isomorphic to the total space of the bundle
![]() $O(1)$
, that is, we have the commutative diagram
$O(1)$
, that is, we have the commutative diagram

Let
![]() ${\mathcal{I}}_{\mathfrak{C}}$
denote the ideal sheaf of
${\mathcal{I}}_{\mathfrak{C}}$
denote the ideal sheaf of
![]() $\mathfrak{C}$
in
$\mathfrak{C}$
in
![]() $\tilde{E}_{2}$
, and define
$\tilde{E}_{2}$
, and define
![]() ${\mathcal{I}}_{O(1)}$
similarly. The normal bundle
${\mathcal{I}}_{O(1)}$
similarly. The normal bundle
![]() $N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
of the subscheme
$N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
of the subscheme
![]() $O(1)$
in
$O(1)$
in
![]() $\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
is
$\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
is
![]() $\unicode[STIX]{x1D70B}^{\ast }O(-1)_{|O(1)}$
. The restriction of
$\unicode[STIX]{x1D70B}^{\ast }O(-1)_{|O(1)}$
. The restriction of
![]() $\unicode[STIX]{x1D70B}^{\ast }O(1)_{|O(1)}$
to
$\unicode[STIX]{x1D70B}^{\ast }O(1)_{|O(1)}$
to
![]() $O(1)-\{0_{O(1)}\}$
is trivialized by the tautological section
$O(1)-\{0_{O(1)}\}$
is trivialized by the tautological section
![]() $s$
of
$s$
of
![]() $\unicode[STIX]{x1D70B}^{\ast }O(1)_{|O(1)}$
over
$\unicode[STIX]{x1D70B}^{\ast }O(1)_{|O(1)}$
over
![]() $O(1)$
, which induces a nowhere vanishing dual section
$O(1)$
, which induces a nowhere vanishing dual section
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}s$
of the dual
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}s$
of the dual
![]() $N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
over
$N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
over
![]() $O(1)-\{0_{O(1)}\}$
. This gives us the section
$O(1)-\{0_{O(1)}\}$
. This gives us the section
![]() $\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle$
of the twisted Grothendieck–Witt sheaf
$\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle$
of the twisted Grothendieck–Witt sheaf
![]() ${\mathcal{G}}{\mathcal{W}}(O(-1))$
over
${\mathcal{G}}{\mathcal{W}}(O(-1))$
over
![]() $O(1)-\{0_{O(1)}\}$
, as the class of the
$O(1)-\{0_{O(1)}\}$
, as the class of the
![]() $O(-1)$
-valued quadratic form
$O(-1)$
-valued quadratic form
![]() $q_{s}$
with
$q_{s}$
with
![]() $q_{s}(1)=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}s$
.
$q_{s}(1)=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}s$
.
The boundary
![]() $\unicode[STIX]{x2202}_{0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}}(\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle )$
lives in
$\unicode[STIX]{x2202}_{0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}}(\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle )$
lives in
![]() $H^{0} (\!0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}},{\mathcal{K}}_{-1}^{MW}(\operatorname{det}(\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}))$
; the canonical trivialization of
$H^{0} (\!0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}},{\mathcal{K}}_{-1}^{MW}(\operatorname{det}(\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}))$
; the canonical trivialization of
![]() $\operatorname{det}E_{2}$
sets this equal to
$\operatorname{det}E_{2}$
sets this equal to
![]() $H^{0}(0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}},{\mathcal{K}}_{-1}^{MW})$
. We claim that a calculation in local coordinates gives the identity
$H^{0}(0_{\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}},{\mathcal{K}}_{-1}^{MW})$
. We claim that a calculation in local coordinates gives the identity
Indeed, take a local generator
![]() $\unicode[STIX]{x1D706}$
for
$\unicode[STIX]{x1D706}$
for
![]() $O(1)$
over
$O(1)$
over
![]() $U\subset B\mathbb{G}_{m}$
, giving the dual local generator
$U\subset B\mathbb{G}_{m}$
, giving the dual local generator
![]() $\unicode[STIX]{x1D706}^{\vee }$
for
$\unicode[STIX]{x1D706}^{\vee }$
for
![]() $O(-1)=O(1)^{\vee }$
. This gives a local isomorphism of
$O(-1)=O(1)^{\vee }$
. This gives a local isomorphism of
![]() $\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
with
$\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}$
with
with
![]() $O(1)=\mathbb{A}^{1}\times 0\times U$
,
$O(1)=\mathbb{A}^{1}\times 0\times U$
,
![]() $O(-1)=0\times \mathbb{A}^{1}\times U$
. This also identifies
$O(-1)=0\times \mathbb{A}^{1}\times U$
. This also identifies
![]() $N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
with the trivial bundle on
$N_{O(1)/\unicode[STIX]{x1D719}^{\ast }\tilde{E}_{2}}$
with the trivial bundle on
![]() $\mathbb{A}^{1}\times 0\times U$
and the section
$\mathbb{A}^{1}\times 0\times U$
and the section
![]() $\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle$
goes over to
$\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle$
goes over to
![]() $\langle 1\rangle \otimes x^{-1}=p_{1}^{\ast }\langle x\rangle$
and the canonical generator of the normal bundle of
$\langle 1\rangle \otimes x^{-1}=p_{1}^{\ast }\langle x\rangle$
and the canonical generator of the normal bundle of
![]() $0_{O(1)}$
in
$0_{O(1)}$
in
![]() $O(1)$
goes over to
$O(1)$
goes over to
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x$
. On
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x$
. On
![]() $\mathbb{A}^{1}=\text{Spec }k[x]$
, the element
$\mathbb{A}^{1}=\text{Spec }k[x]$
, the element
![]() $\langle x\rangle \in K_{0}^{MW}(k[x])$
has boundary
$\langle x\rangle \in K_{0}^{MW}(k[x])$
has boundary
since
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x}([x])=1$
. Under the canonical identification
$\unicode[STIX]{x2202}_{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x}([x])=1$
. Under the canonical identification
![]() ${\mathcal{K}}_{-1}^{MW}\cong {\mathcal{W}}$
,
${\mathcal{K}}_{-1}^{MW}\cong {\mathcal{W}}$
,
![]() $\unicode[STIX]{x1D702}$
goes over to
$\unicode[STIX]{x1D702}$
goes over to
![]() $\langle 1\rangle$
. We refer the reader to [Reference Morel30, § 6] or [Reference Morel31, § 6] for details on the Milnor–Witt sheaves and their relation to
$\langle 1\rangle$
. We refer the reader to [Reference Morel30, § 6] or [Reference Morel31, § 6] for details on the Milnor–Witt sheaves and their relation to
![]() ${\mathcal{G}}{\mathcal{W}}$
and
${\mathcal{G}}{\mathcal{W}}$
and
![]() ${\mathcal{W}}$
.
${\mathcal{W}}$
.
Identifying
![]() $\mathfrak{C}-\{0_{\tilde{E}_{2}}\}$
with
$\mathfrak{C}-\{0_{\tilde{E}_{2}}\}$
with
![]() $O(1)-\{0_{O(1)}\}$
via
$O(1)-\{0_{O(1)}\}$
via
![]() $\unicode[STIX]{x1D719}$
, we have the section
$\unicode[STIX]{x1D719}$
, we have the section
![]() $\unicode[STIX]{x1D719}_{\ast }(\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle )$
of
$\unicode[STIX]{x1D719}_{\ast }(\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}s\rangle )$
of
![]() ${\mathcal{W}}(N_{\mathfrak{C}-\{0_{\tilde{E}_{2}}\}/\tilde{E}_{2}})$
over
${\mathcal{W}}(N_{\mathfrak{C}-\{0_{\tilde{E}_{2}}\}/\tilde{E}_{2}})$
over
![]() $\mathfrak{C}-\{0_{\tilde{E}_{2}}\}$
. This has boundary
$\mathfrak{C}-\{0_{\tilde{E}_{2}}\}$
. This has boundary
where
![]() $s_{0}:BN\rightarrow \tilde{E}_{2}$
is the 0-section. Since
$s_{0}:BN\rightarrow \tilde{E}_{2}$
is the 0-section. Since
![]() $\unicode[STIX]{x1D719}:B\mathbb{G}_{m}\rightarrow BN$
is the double cover
$\unicode[STIX]{x1D719}:B\mathbb{G}_{m}\rightarrow BN$
is the double cover
![]() $\text{Spec }_{{\mathcal{O}}_{BN}}({\mathcal{O}}_{BN}(\sqrt{p_{1}^{\ast }Q}))$
,
$\text{Spec }_{{\mathcal{O}}_{BN}}({\mathcal{O}}_{BN}(\sqrt{p_{1}^{\ast }Q}))$
,
![]() $\unicode[STIX]{x1D719}_{\ast }\langle 1\rangle$
is just the image in
$\unicode[STIX]{x1D719}_{\ast }\langle 1\rangle$
is just the image in
![]() $H^{0}(BN,{\mathcal{W}})$
of the trace form of this double cover, which gives us the element
$H^{0}(BN,{\mathcal{W}})$
of the trace form of this double cover, which gives us the element
![]() $\langle 2\rangle +\langle 2\bar{q}\rangle =\langle 2\rangle (1+\langle \bar{q}\rangle )$
.
$\langle 2\rangle +\langle 2\bar{q}\rangle =\langle 2\rangle (1+\langle \bar{q}\rangle )$
.
Let
![]() $\tilde{E}_{2,m}$
denote the pullback to
$\tilde{E}_{2,m}$
denote the pullback to
![]() $B_{m}\operatorname{SL}_{2}\subset \operatorname{BSL}_{2}$
. We recall that
$B_{m}\operatorname{SL}_{2}\subset \operatorname{BSL}_{2}$
. We recall that
![]() $H^{\ast }(\tilde{E}_{2,m},{\mathcal{W}})$
may be computed as the cohomology of the Rost–Schmid complex (see [Reference Morel29, Chapter 5])
$H^{\ast }(\tilde{E}_{2,m},{\mathcal{W}})$
may be computed as the cohomology of the Rost–Schmid complex (see [Reference Morel29, Chapter 5])
 $$\begin{eqnarray}\displaystyle {\mathcal{W}}(k(\tilde{E}_{2,m})) & \rightarrow & \displaystyle \bigoplus _{x\in \tilde{E}_{2,m}^{(1)}}{\mathcal{W}}(k(x),\operatorname{det}N_{x/\tilde{E}_{2,m}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \bigoplus _{x\in \tilde{E}_{2,m}^{(2)}}{\mathcal{W}}(k(x),\operatorname{det}N_{x/\tilde{E}_{2,m}})\rightarrow \cdots \,.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{W}}(k(\tilde{E}_{2,m})) & \rightarrow & \displaystyle \bigoplus _{x\in \tilde{E}_{2,m}^{(1)}}{\mathcal{W}}(k(x),\operatorname{det}N_{x/\tilde{E}_{2,m}})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \bigoplus _{x\in \tilde{E}_{2,m}^{(2)}}{\mathcal{W}}(k(x),\operatorname{det}N_{x/\tilde{E}_{2,m}})\rightarrow \cdots \,.\nonumber\end{eqnarray}$$
To simplify the notation, we replace
![]() $\tilde{E}_{2,m}$
with
$\tilde{E}_{2,m}$
with
![]() $\tilde{E}_{2}$
, with the understanding that all objects should be considered as living on
$\tilde{E}_{2}$
, with the understanding that all objects should be considered as living on
![]() $\tilde{E}_{2,m}$
for arbitrary
$\tilde{E}_{2,m}$
for arbitrary
![]() $m$
.
$m$
.
We note that
![]() $s_{0\ast }(1)\in H^{2}(\tilde{E}_{2},{\mathcal{W}})$
is represented in the Rost–Schmid complex by the constant section
$s_{0\ast }(1)\in H^{2}(\tilde{E}_{2},{\mathcal{W}})$
is represented in the Rost–Schmid complex by the constant section
![]() $1$
on
$1$
on
![]() $0_{\tilde{E}_{2}}$
. Computing
$0_{\tilde{E}_{2}}$
. Computing
![]() $H^{2}(\tilde{E}_{2},{\mathcal{W}})$
via the Rost–Schmid complex, we see that
$H^{2}(\tilde{E}_{2},{\mathcal{W}})$
via the Rost–Schmid complex, we see that
goes to zero in
![]() $H^{2}(\tilde{E},{\mathcal{W}})$
. As
$H^{2}(\tilde{E},{\mathcal{W}})$
. As
![]() $p^{\ast }e=e(\tilde{E}_{2})=s_{0}^{\ast }s_{0\ast }(1)$
, and as
$p^{\ast }e=e(\tilde{E}_{2})=s_{0}^{\ast }s_{0\ast }(1)$
, and as
![]() $s_{0}^{\ast }:H^{2}(\tilde{E}_{2},{\mathcal{W}})\rightarrow H^{2}(BN,{\mathcal{W}})$
is an isomorphism, we see that
$s_{0}^{\ast }:H^{2}(\tilde{E}_{2},{\mathcal{W}})\rightarrow H^{2}(BN,{\mathcal{W}})$
is an isomorphism, we see that
![]() $\langle 2\rangle (1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
in
$\langle 2\rangle (1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
in
![]() $H^{2}(BN,{\mathcal{W}})$
; since
$H^{2}(BN,{\mathcal{W}})$
; since
![]() $\langle 2\rangle$
is a unit in
$\langle 2\rangle$
is a unit in
![]() ${\mathcal{W}}$
, it follows that
${\mathcal{W}}$
, it follows that
![]() $(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
.
$(1+\langle \bar{q}\rangle )\cdot p^{\ast }e=0$
.
Proposition 5.5. Let
![]() $W(k)[x_{0},x_{2}]$
be the graded polynomial algebra over
$W(k)[x_{0},x_{2}]$
be the graded polynomial algebra over
![]() $W(k)$
on generators
$W(k)$
on generators
![]() $x_{0},x_{2}$
, with
$x_{0},x_{2}$
, with
![]() $\deg x_{i}=i$
. Then sending
$\deg x_{i}=i$
. Then sending
![]() $x_{0}$
to
$x_{0}$
to
![]() $\langle \bar{q}\rangle$
and
$\langle \bar{q}\rangle$
and
![]() $x_{2}$
to
$x_{2}$
to
![]() $p^{\ast }e$
defines
$p^{\ast }e$
defines
![]() $W(k)$
-algebra isomorphism
$W(k)$
-algebra isomorphism
Moreover,
![]() $H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is the quotient of the free
$H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
is the quotient of the free
![]() $H^{\ast }(BN,{\mathcal{W}})$
-module on the generator
$H^{\ast }(BN,{\mathcal{W}})$
-module on the generator
![]() $j^{\ast }e({\mathcal{T}})$
modulo the relation
$j^{\ast }e({\mathcal{T}})$
modulo the relation
![]() $(1+\langle q\rangle )j^{\ast }e({\mathcal{T}})=0$
.
$(1+\langle q\rangle )j^{\ast }e({\mathcal{T}})=0$
.
Proof. It follows from Lemma 5.4 and the fact that
![]() $\langle \bar{q}\rangle$
is represented locally by a one-dimensional form that
$\langle \bar{q}\rangle$
is represented locally by a one-dimensional form that
![]() $\unicode[STIX]{x1D713}$
is a well-defined
$\unicode[STIX]{x1D713}$
is a well-defined
![]() $W(k)$
-algebra homomorphism. It follows from Proposition 5.3 that
$W(k)$
-algebra homomorphism. It follows from Proposition 5.3 that
![]() $\unicode[STIX]{x1D713}$
is a
$\unicode[STIX]{x1D713}$
is a
![]() $W(k)$
-module isomorphism, hence a
$W(k)$
-module isomorphism, hence a
![]() $W(k)$
-algebra isomorphism. The description of
$W(k)$
-algebra isomorphism. The description of
![]() $H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
as an
$H^{\ast }(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
as an
![]() $H^{\ast }(BN,{\mathcal{W}})$
-module then follows from Proposition 5.3 and Lemma 5.4.
$H^{\ast }(BN,{\mathcal{W}})$
-module then follows from Proposition 5.3 and Lemma 5.4.
As
![]() $Q$
is a section of
$Q$
is a section of
![]() ${\mathcal{O}}_{\mathbb{P}(\operatorname{Sym}^{2}F)}(2)$
,
${\mathcal{O}}_{\mathbb{P}(\operatorname{Sym}^{2}F)}(2)$
,
![]() $p_{1}^{\ast }Q$
has a well-defined value in
$p_{1}^{\ast }Q$
has a well-defined value in
![]() $k/k^{\times 2}$
at each point of
$k/k^{\times 2}$
at each point of
![]() $BN(k)$
. Here we use the definition of
$BN(k)$
. Here we use the definition of
![]() $BN$
as an Ind-scheme to define
$BN$
as an Ind-scheme to define
![]() $BN(k)$
.
$BN(k)$
.
Lemma 5.6. Let
![]() $x\in BN(k)$
be a
$x\in BN(k)$
be a
![]() $k$
-point such that
$k$
-point such that
![]() $p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
, and let
$p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
, and let
![]() $\tilde{E}_{2x}$
denote the fiber of
$\tilde{E}_{2x}$
denote the fiber of
![]() $\tilde{E}_{2}$
at
$\tilde{E}_{2}$
at
![]() $x$
with origin
$x$
with origin
![]() $0_{x}$
. Let
$0_{x}$
. Let
denote the Thom isomorphism. Then the restriction map
induces an isomorphism
Proof. Since
![]() $p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
, it follows that
$p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
, it follows that
![]() $i_{x}^{\ast }(1+\langle \bar{q}\rangle )=1+\langle -1\rangle =0$
in
$i_{x}^{\ast }(1+\langle \bar{q}\rangle )=1+\langle -1\rangle =0$
in
![]() $W(k)$
. Thus
$W(k)$
. Thus
so we have a well-defined homomorphism
We have the decomposition
and thus the restriction of the Thom isomorphism
![]() $s_{0\ast }:H^{0}(BN,{\mathcal{W}})\rightarrow H_{0_{\tilde{E}_{2}}}^{2}(\tilde{E}_{2},{\mathcal{W}})$
to the factor
$s_{0\ast }:H^{0}(BN,{\mathcal{W}})\rightarrow H_{0_{\tilde{E}_{2}}}^{2}(\tilde{E}_{2},{\mathcal{W}})$
to the factor
![]() $W(k)$
induces an isomorphism
$W(k)$
induces an isomorphism
As the composition
![]() $\bar{i}_{x}^{\ast }\circ \bar{s}_{0\ast }$
is just the Thom isomorphism
$\bar{i}_{x}^{\ast }\circ \bar{s}_{0\ast }$
is just the Thom isomorphism
the result follows.
6 Rank two bundles on
 $BN_{T}(\operatorname{SL}_{2})$
$BN_{T}(\operatorname{SL}_{2})$
We pursue an analogy of
![]() $N:=N_{T}(\operatorname{SL}_{2})$
with
$N:=N_{T}(\operatorname{SL}_{2})$
with
![]() $\text{O}(2)$
. We let
$\text{O}(2)$
. We let
be the isomorphism
and set
For
![]() $m\geqslant 1$
an integer, define the representations
$m\geqslant 1$
an integer, define the representations
![]() $(F(m),\unicode[STIX]{x1D70C}_{m})$
of
$(F(m),\unicode[STIX]{x1D70C}_{m})$
of
![]() $N$
by
$N$
by
![]() $F(m)=\mathbb{A}^{2}$
and
$F(m)=\mathbb{A}^{2}$
and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{m}\left(\begin{array}{@{}cc@{}}t & 0\\ 0 & t^{-1}\end{array}\right) & = & \displaystyle \left(\begin{array}{@{}cc@{}}t^{m} & 0\\ 0 & t^{-m}\end{array}\right)\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{m}(\unicode[STIX]{x1D70E}) & = & \displaystyle \left(\begin{array}{@{}cc@{}}0 & 1\\ (-1)^{m} & 0\end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{m}\left(\begin{array}{@{}cc@{}}t & 0\\ 0 & t^{-1}\end{array}\right) & = & \displaystyle \left(\begin{array}{@{}cc@{}}t^{m} & 0\\ 0 & t^{-m}\end{array}\right)\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{m}(\unicode[STIX]{x1D70E}) & = & \displaystyle \left(\begin{array}{@{}cc@{}}0 & 1\\ (-1)^{m} & 0\end{array}\right).\nonumber\end{eqnarray}$$
We let
![]() $(\unicode[STIX]{x1D70C}_{0},F(0))$
denote trivial one-dimensional representation.
$(\unicode[STIX]{x1D70C}_{0},F(0))$
denote trivial one-dimensional representation.
For
![]() $m\geqslant 0$
, we let
$m\geqslant 0$
, we let
![]() $\unicode[STIX]{x1D70C}_{m}^{-}:N\rightarrow \operatorname{SL}_{2}$
be the representation given by
$\unicode[STIX]{x1D70C}_{m}^{-}:N\rightarrow \operatorname{SL}_{2}$
be the representation given by
We let
![]() $p^{(m)}:\tilde{O} (m)\rightarrow BN$
denote the rank two vector bundle
$p^{(m)}:\tilde{O} (m)\rightarrow BN$
denote the rank two vector bundle
corresponding to
![]() $\unicode[STIX]{x1D70C}_{m}$
, with zero-section
$\unicode[STIX]{x1D70C}_{m}$
, with zero-section
![]() $s_{0}^{(m)}:BN\rightarrow \tilde{O} (m)$
and let
$s_{0}^{(m)}:BN\rightarrow \tilde{O} (m)$
and let
![]() $\operatorname{th}^{(m)}\in H_{0_{\tilde{O} (m)}}^{2}(\tilde{O} (m)),{\mathcal{W}}(\operatorname{det}^{-1}(\tilde{O} (m)))$
denote the Thom class
$\operatorname{th}^{(m)}\in H_{0_{\tilde{O} (m)}}^{2}(\tilde{O} (m)),{\mathcal{W}}(\operatorname{det}^{-1}(\tilde{O} (m)))$
denote the Thom class
![]() $s_{0\ast }^{(m)}(1)$
. We define the bundle
$s_{0\ast }^{(m)}(1)$
. We define the bundle
![]() $p^{(m)-}:\tilde{O} ^{-}(m)\rightarrow BN$
replacing
$p^{(m)-}:\tilde{O} ^{-}(m)\rightarrow BN$
replacing
![]() $\unicode[STIX]{x1D70C}_{m}$
with
$\unicode[STIX]{x1D70C}_{m}$
with
![]() $\unicode[STIX]{x1D70C}_{m}^{-}$
. We note that
$\unicode[STIX]{x1D70C}_{m}^{-}$
. We note that
![]() $\text{Pic}(BN)\cong \mathbb{Z}/2$
, with generator
$\text{Pic}(BN)\cong \mathbb{Z}/2$
, with generator
![]() $\unicode[STIX]{x1D6FE}:=\tilde{O} ^{-}(0)$
and that we have canonical isomorphisms
$\unicode[STIX]{x1D6FE}:=\tilde{O} ^{-}(0)$
and that we have canonical isomorphisms
![]() $\operatorname{det}\tilde{O} ^{\pm }(m)\cong O_{BN}$
for
$\operatorname{det}\tilde{O} ^{\pm }(m)\cong O_{BN}$
for
![]() $m$
odd and
$m$
odd and
![]() $\operatorname{det}\tilde{O} ^{\pm }(m)\cong \unicode[STIX]{x1D6FE}$
for
$\operatorname{det}\tilde{O} ^{\pm }(m)\cong \unicode[STIX]{x1D6FE}$
for
![]() $m>0$
even.
$m>0$
even.
Our goal in this section is to compute the Euler classes
![]() $e(\tilde{O} ^{\pm }(m))\in H^{2}(BN,{\mathcal{W}}(\operatorname{det}^{-1}(\tilde{O} ^{\pm }(m))))$
.
$e(\tilde{O} ^{\pm }(m))\in H^{2}(BN,{\mathcal{W}}(\operatorname{det}^{-1}(\tilde{O} ^{\pm }(m))))$
.
Lemma 6.1.
![]() $\tilde{O} (2)$
is isomorphic to
$\tilde{O} (2)$
is isomorphic to
![]() $j^{\ast }{\mathcal{T}}$
and therefore
$j^{\ast }{\mathcal{T}}$
and therefore
![]() $e(\tilde{O} (2))=j^{\ast }e({\mathcal{T}})$
.
$e(\tilde{O} (2))=j^{\ast }e({\mathcal{T}})$
.
Proof. The quotient map
![]() $\unicode[STIX]{x1D70B}:\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}^{2}-C$
is étale and we have
$\unicode[STIX]{x1D70B}:\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}^{2}-C$
is étale and we have
![]() $\unicode[STIX]{x1D70B}^{\ast }T_{\mathbb{P}^{2}-C}\cong T_{\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}}\cong p_{1}^{\ast }T_{\mathbb{P}^{1}}\oplus p_{2}^{\ast }T_{\mathbb{P}^{1}}\cong p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
. Under the inclusion
$\unicode[STIX]{x1D70B}^{\ast }T_{\mathbb{P}^{2}-C}\cong T_{\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}}\cong p_{1}^{\ast }T_{\mathbb{P}^{1}}\oplus p_{2}^{\ast }T_{\mathbb{P}^{1}}\cong p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
. Under the inclusion
![]() $T(\operatorname{SL}_{2})\rightarrow T(\operatorname{GL}_{2})$
, the restriction of
$T(\operatorname{SL}_{2})\rightarrow T(\operatorname{GL}_{2})$
, the restriction of
![]() $\unicode[STIX]{x1D70C}_{2}$
to
$\unicode[STIX]{x1D70C}_{2}$
to
![]() $T(\operatorname{SL}_{2})$
is the restriction of the two-dimensional representation of
$T(\operatorname{SL}_{2})$
is the restriction of the two-dimensional representation of
![]() $T(\operatorname{GL}_{2})=\mathbb{G}_{m}\times \mathbb{G}_{m}$
defining
$T(\operatorname{GL}_{2})=\mathbb{G}_{m}\times \mathbb{G}_{m}$
defining
![]() $p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
, and the action of
$p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
, and the action of
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $\unicode[STIX]{x1D70B}^{\ast }T_{\mathbb{P}^{2}-C}=p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
is via
$\unicode[STIX]{x1D70B}^{\ast }T_{\mathbb{P}^{2}-C}=p_{1}^{\ast }O_{\mathbb{P}^{1}}(2)\oplus p_{2}^{\ast }O_{\mathbb{P}^{1}}(2)$
is via
![]() $\unicode[STIX]{x1D70C}_{2}(\unicode[STIX]{x1D70E})$
.
$\unicode[STIX]{x1D70C}_{2}(\unicode[STIX]{x1D70E})$
.
Let
![]() $R$
be a
$R$
be a
![]() $k$
-algebra, essentially of finite type over
$k$
-algebra, essentially of finite type over
![]() $k$
. We consider an
$k$
. We consider an
![]() $R$
-valued point
$R$
-valued point
![]() $x$
of
$x$
of
![]() $B_{n}\operatorname{SL}_{2}$
coming from an
$B_{n}\operatorname{SL}_{2}$
coming from an
![]() $R$
-valued point of
$R$
-valued point of
![]() $E_{n}\operatorname{SL}_{2}$
, namely, two elements
$E_{n}\operatorname{SL}_{2}$
, namely, two elements
![]() $v_{1},v_{2}\in \mathbb{A}^{n+2}(R)$
such that the resulting matrix
$v_{1},v_{2}\in \mathbb{A}^{n+2}(R)$
such that the resulting matrix
![]() $(\!\begin{smallmatrix}v_{1}\\ v_{2}\end{smallmatrix}\!)$
has rank two at each maximal ideal of
$(\!\begin{smallmatrix}v_{1}\\ v_{2}\end{smallmatrix}\!)$
has rank two at each maximal ideal of
![]() $R$
. This gives us the corresponding
$R$
. This gives us the corresponding
![]() $R$
-valued point
$R$
-valued point
![]() $\bar{x}$
of the Grassmannian
$\bar{x}$
of the Grassmannian
![]() $\operatorname{Gr}(2,n+2)$
,
$\operatorname{Gr}(2,n+2)$
,
together with the isomorphism of
![]() $R$
-modules
$R$
-modules
![]() $R\cong \operatorname{det}\bar{x}^{\ast }E_{2}$
sending
$R\cong \operatorname{det}\bar{x}^{\ast }E_{2}$
sending
![]() $1\in R$
to
$1\in R$
to
![]() $v_{1}\wedge v_{2}$
.
$v_{1}\wedge v_{2}$
.
We have the
![]() $m$
th-power map
$m$
th-power map
which is a (nonlinear!)
![]() $N$
-equivariant morphism. This gives us the flat and finite map of
$N$
-equivariant morphism. This gives us the flat and finite map of
![]() $BN$
-schemes
$BN$
-schemes
For
![]() $V\rightarrow X$
a rank
$V\rightarrow X$
a rank
![]() $r$
vector bundle with trivialized determinant
$r$
vector bundle with trivialized determinant
![]() $\unicode[STIX]{x1D703}:\operatorname{det}V\rightarrow O_{X}$
and 0-section
$\unicode[STIX]{x1D703}:\operatorname{det}V\rightarrow O_{X}$
and 0-section
![]() $s_{0}:X\rightarrow V$
, we write
$s_{0}:X\rightarrow V$
, we write
![]() $s_{0\ast }:{\mathcal{E}}^{a,b}(X)\rightarrow {\mathcal{E}}_{0_{V}}^{a+2r,b+r}(V;\operatorname{det}^{-1}V)$
for the Thom isomorphism.
$s_{0\ast }:{\mathcal{E}}^{a,b}(X)\rightarrow {\mathcal{E}}_{0_{V}}^{a+2r,b+r}(V;\operatorname{det}^{-1}V)$
for the Thom isomorphism.
Lemma 6.2. For
![]() $m$
odd,
$m$
odd,
![]() $e(\tilde{O} (m))=s_{0}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)}))$
and for
$e(\tilde{O} (m))=s_{0}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)}))$
and for
![]() $m$
even,
$m$
even,
![]() $e(\tilde{O} (m))=s_{0}^{(2)\ast }(\unicode[STIX]{x1D713}_{m/2,2}^{\ast }(\operatorname{th}^{(m)}))$
.
$e(\tilde{O} (m))=s_{0}^{(2)\ast }(\unicode[STIX]{x1D713}_{m/2,2}^{\ast }(\operatorname{th}^{(m)}))$
.
Proof. For
![]() $m$
odd, we have
$m$
odd, we have
![]() $s_{0}^{(m)}=\unicode[STIX]{x1D713}_{m,1}\circ s_{0}^{(1)}$
, hence
$s_{0}^{(m)}=\unicode[STIX]{x1D713}_{m,1}\circ s_{0}^{(1)}$
, hence
 $$\begin{eqnarray}\displaystyle e(\tilde{O} (m)) & = & \displaystyle s_{0}^{(m)\ast }(\operatorname{th}^{(m)})\nonumber\\ \displaystyle & = & \displaystyle s_{0}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e(\tilde{O} (m)) & = & \displaystyle s_{0}^{(m)\ast }(\operatorname{th}^{(m)})\nonumber\\ \displaystyle & = & \displaystyle s_{0}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)})).\nonumber\end{eqnarray}$$
The proof for
![]() $m$
even is the same.
$m$
even is the same.
Via the isomorphisms

we write, for
![]() $m$
odd,
$m$
odd,
and for
![]() $m$
even
$m$
even
uniquely defining the elements
![]() $a_{m},b_{m}\in W(k)$
.
$a_{m},b_{m}\in W(k)$
.
Lemma 6.3. For
![]() $m$
odd,
$m$
odd,
![]() $e(\tilde{O} (m))=(a_{m}-b_{m})p^{\ast }e\in H^{2}(BN,{\mathcal{W}})$
and for
$e(\tilde{O} (m))=(a_{m}-b_{m})p^{\ast }e\in H^{2}(BN,{\mathcal{W}})$
and for
![]() $m$
even,
$m$
even,
![]() $e(\tilde{O} (m))=(a_{m}-b_{m})e(\tilde{O} (2))\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
$e(\tilde{O} (m))=(a_{m}-b_{m})e(\tilde{O} (2))\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
Proof. For
![]() $m$
odd, the composition
$m$
odd, the composition

is multiplication with
![]() $e(\tilde{O} (1))=p^{\ast }e$
. Since
$e(\tilde{O} (1))=p^{\ast }e$
. Since
![]() $(1+\langle \bar{q}\rangle )p^{\ast }e=0$
, we see that
$(1+\langle \bar{q}\rangle )p^{\ast }e=0$
, we see that
![]() $a_{m}+b_{m}\cdot \langle \bar{q}\rangle$
gets sent to
$a_{m}+b_{m}\cdot \langle \bar{q}\rangle$
gets sent to
![]() $(a_{m}-b_{m})p^{\ast }e$
.
$(a_{m}-b_{m})p^{\ast }e$
.
Replacing
![]() $e(\tilde{O} (1))$
with
$e(\tilde{O} (1))$
with
![]() $e(\tilde{O} (2))$
and using
$e(\tilde{O} (2))$
and using
![]() $\unicode[STIX]{x1D6FE}$
-twisted cohomology, the proof for
$\unicode[STIX]{x1D6FE}$
-twisted cohomology, the proof for
![]() $m$
even is the same, using the relation
$m$
even is the same, using the relation
![]() $(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
and Lemma 6.1.
$(1+\langle \bar{q}\rangle )\cdot j^{\ast }e({\mathcal{T}})=0$
and Lemma 6.1.
Choose a point
![]() $x\in BN(k)$
with
$x\in BN(k)$
with
![]() $p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
. Write
$p_{1}^{\ast }Q(x)=-1\,\text{mod}\,k^{\times 2}$
. Write
![]() $\tilde{O} (m)_{x}$
for the fiber of
$\tilde{O} (m)_{x}$
for the fiber of
![]() $\tilde{O} (m)$
at
$\tilde{O} (m)$
at
![]() $x$
and let
$x$
and let
denote the inclusion. Take
![]() $m$
odd and let
$m$
odd and let
the restriction of
![]() $\unicode[STIX]{x1D713}_{m,1}$
. The map
$\unicode[STIX]{x1D713}_{m,1}$
. The map
induces an isomorphism
We write
![]() $\operatorname{th}_{x}^{(m)}:=s_{0x\ast }^{(m)}(1)$
.
$\operatorname{th}_{x}^{(m)}:=s_{0x\ast }^{(m)}(1)$
.
For
![]() $m$
even, we have
$m$
even, we have
![]() $\unicode[STIX]{x1D713}_{m/2,2}(x):\tilde{O} (2)_{x}\rightarrow \tilde{O} (m)_{x}$
and
$\unicode[STIX]{x1D713}_{m/2,2}(x):\tilde{O} (2)_{x}\rightarrow \tilde{O} (m)_{x}$
and
![]() $s_{0x}^{(m)}$
induces an isomorphism
$s_{0x}^{(m)}$
induces an isomorphism
Lemma 6.4. For
![]() $m$
odd,
$m$
odd,
![]() $s_{0x\ast }^{(1)}(a_{m}-b_{m})=\unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(\operatorname{th}_{x}^{(m)})=\unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(s_{0x\ast }^{(m)}(1))$
and for
$s_{0x\ast }^{(1)}(a_{m}-b_{m})=\unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(\operatorname{th}_{x}^{(m)})=\unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(s_{0x\ast }^{(m)}(1))$
and for
![]() $m$
even,
$m$
even,
![]() $s_{0x\ast }^{(2)}(a_{m}-b_{m})=\unicode[STIX]{x1D713}_{m/2,2}(x)^{\ast }(\operatorname{th}_{x}^{(m)})=\unicode[STIX]{x1D713}_{m/2.2}(x)^{\ast }(s_{0x\ast }^{(m)}(1))$
.
$s_{0x\ast }^{(2)}(a_{m}-b_{m})=\unicode[STIX]{x1D713}_{m/2,2}(x)^{\ast }(\operatorname{th}_{x}^{(m)})=\unicode[STIX]{x1D713}_{m/2.2}(x)^{\ast }(s_{0x\ast }^{(m)}(1))$
.
Proof. For
![]() $m$
odd, the second identity is just the definition of
$m$
odd, the second identity is just the definition of
![]() $\operatorname{th}_{x}^{(m)}$
. We have the commutative diagrams
$\operatorname{th}_{x}^{(m)}$
. We have the commutative diagrams

and
The map
![]() $x^{\ast }:H^{0}(BN,{\mathcal{W}})\rightarrow W(k)$
is the identity on the summand
$x^{\ast }:H^{0}(BN,{\mathcal{W}})\rightarrow W(k)$
is the identity on the summand
![]() $W(k)$
of
$W(k)$
of
![]() $H^{0}(BN,{\mathcal{W}})$
and is the map
$H^{0}(BN,{\mathcal{W}})$
and is the map
![]() $b\cdot \langle \bar{q}\rangle \mapsto -b$
on the summand
$b\cdot \langle \bar{q}\rangle \mapsto -b$
on the summand
![]() $W(k)\cdot \langle \bar{q}\rangle$
, because
$W(k)\cdot \langle \bar{q}\rangle$
, because
![]() $x^{\ast }(\langle \bar{q}\rangle )=\langle -1\rangle =-1\in W(k)$
.
$x^{\ast }(\langle \bar{q}\rangle )=\langle -1\rangle =-1\in W(k)$
.
Via the respective Thom isomorphisms
and
we see that
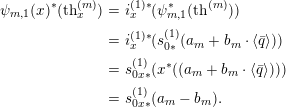 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(\operatorname{th}_{x}^{(m)}) & = & \displaystyle i_{x}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)}))\nonumber\\ \displaystyle & = & \displaystyle i_{x}^{(1)\ast }(s_{0\ast }^{(1)}(a_{m}+b_{m}\cdot \langle \bar{q}\rangle ))\nonumber\\ \displaystyle & = & \displaystyle s_{0x\ast }^{(1)}(x^{\ast }((a_{m}+b_{m}\cdot \langle \bar{q}\rangle )))\nonumber\\ \displaystyle & = & \displaystyle s_{0x\ast }^{(1)}(a_{m}-b_{m}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,1}(x)^{\ast }(\operatorname{th}_{x}^{(m)}) & = & \displaystyle i_{x}^{(1)\ast }(\unicode[STIX]{x1D713}_{m,1}^{\ast }(\operatorname{th}^{(m)}))\nonumber\\ \displaystyle & = & \displaystyle i_{x}^{(1)\ast }(s_{0\ast }^{(1)}(a_{m}+b_{m}\cdot \langle \bar{q}\rangle ))\nonumber\\ \displaystyle & = & \displaystyle s_{0x\ast }^{(1)}(x^{\ast }((a_{m}+b_{m}\cdot \langle \bar{q}\rangle )))\nonumber\\ \displaystyle & = & \displaystyle s_{0x\ast }^{(1)}(a_{m}-b_{m}).\nonumber\end{eqnarray}$$
The proof for
![]() $m$
even is the same.
$m$
even is the same.
Take
![]() $m$
odd. Fixing the point
$m$
odd. Fixing the point
![]() $x\in BN$
as above, we note that the
$x\in BN$
as above, we note that the
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $\tilde{O} (1)_{x}$
and
$\tilde{O} (1)_{x}$
and
![]() $\tilde{O} (m)_{x}$
are both isomorphic to
$\tilde{O} (m)_{x}$
are both isomorphic to
![]() $F=\mathbb{A}_{k}^{2}$
. We have canonical trivializations
$F=\mathbb{A}_{k}^{2}$
. We have canonical trivializations
![]() $\unicode[STIX]{x1D702}_{m}:\operatorname{det}\tilde{O} (m)_{x}\rightarrow k$
,
$\unicode[STIX]{x1D702}_{m}:\operatorname{det}\tilde{O} (m)_{x}\rightarrow k$
,
![]() $\unicode[STIX]{x1D702}_{1}:\operatorname{det}\tilde{O} (1)_{x}\rightarrow k$
. We normalize the trivializations
$\unicode[STIX]{x1D702}_{1}:\operatorname{det}\tilde{O} (1)_{x}\rightarrow k$
. We normalize the trivializations
![]() $\unicode[STIX]{x1D6FC}_{1}:\tilde{O} (1)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
$\unicode[STIX]{x1D6FC}_{1}:\tilde{O} (1)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
by requiring that
$\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
by requiring that
![]() $\operatorname{det}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D702}_{1}^{-1}=\operatorname{det}\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D702}_{m}^{-1}$
in
$\operatorname{det}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D702}_{1}^{-1}=\operatorname{det}\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D702}_{m}^{-1}$
in
![]() $k^{\times }/k^{\times 2}$
; let
$k^{\times }/k^{\times 2}$
; let
![]() $\unicode[STIX]{x1D706}\in k^{\times }/k^{\times 2}$
denote this common value. This gives us the commutative diagram
$\unicode[STIX]{x1D706}\in k^{\times }/k^{\times 2}$
denote this common value. This gives us the commutative diagram

and similarly for
![]() $m=1$
.
$m=1$
.
Via these trivializations, we may therefore consider
![]() $\unicode[STIX]{x1D713}_{m,1}(x)$
as a self-map
$\unicode[STIX]{x1D713}_{m,1}(x)$
as a self-map
inducing the map on the Thom spaces
![]() $\mathbb{A}^{2}/(\mathbb{A}^{2}-\{0\})$
$\mathbb{A}^{2}/(\mathbb{A}^{2}-\{0\})$
Passing to
![]() $\operatorname{SH}(k)$
,
$\operatorname{SH}(k)$
,
![]() $\operatorname{th}(\unicode[STIX]{x1D713}_{m,1}(x))$
gives an endomorphism of the sphere spectrum,
$\operatorname{th}(\unicode[STIX]{x1D713}_{m,1}(x))$
gives an endomorphism of the sphere spectrum,
Let
![]() $\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
$\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
![]() $\unicode[STIX]{x1D6F4}_{T}^{\infty }\operatorname{th}(\unicode[STIX]{x1D713}_{m}(x))$
in
$\unicode[STIX]{x1D6F4}_{T}^{\infty }\operatorname{th}(\unicode[STIX]{x1D713}_{m}(x))$
in
![]() $W(k)$
, via Morel’s isomorphism
$W(k)$
, via Morel’s isomorphism
![]() $\text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})\cong \operatorname{GW}(k)$
and the surjection
$\text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})\cong \operatorname{GW}(k)$
and the surjection
![]() $\operatorname{GW}(k)\rightarrow W(k)$
. It follows from Lemmas 6.3, 6.4 that
$\operatorname{GW}(k)\rightarrow W(k)$
. It follows from Lemmas 6.3, 6.4 that
For
![]() $m$
even, we have a canonical isomorphism
$m$
even, we have a canonical isomorphism
![]() $\unicode[STIX]{x1D702}_{m}:\operatorname{det}\tilde{O} (m)_{x}\rightarrow \unicode[STIX]{x1D6FE}_{x}$
. We take trivializations
$\unicode[STIX]{x1D702}_{m}:\operatorname{det}\tilde{O} (m)_{x}\rightarrow \unicode[STIX]{x1D6FE}_{x}$
. We take trivializations
![]() $\unicode[STIX]{x1D6FC}_{2}:\tilde{O} (2)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
$\unicode[STIX]{x1D6FC}_{2}:\tilde{O} (2)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such that the diagram
$\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such that the diagram
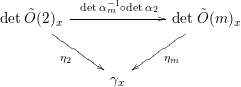
commutes up to multiplication by an element in
![]() $k^{\times 2}$
. Let
$k^{\times 2}$
. Let
![]() $\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
$\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
![]() $\unicode[STIX]{x1D6F4}_{T}^{\infty }\operatorname{th}(\unicode[STIX]{x1D713}_{m/2,2}(x))$
in
$\unicode[STIX]{x1D6F4}_{T}^{\infty }\operatorname{th}(\unicode[STIX]{x1D713}_{m/2,2}(x))$
in
![]() $W(k)$
. Using the fact that
$W(k)$
. Using the fact that
![]() $e(\tilde{O} (2))$
is a
$e(\tilde{O} (2))$
is a
![]() $W(k)$
-generator for
$W(k)$
-generator for
![]() $H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
(Proposition 5.3 and Lemma 6.1), it follows as for odd
$H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
(Proposition 5.3 and Lemma 6.1), it follows as for odd
![]() $m$
that
$m$
that
For
![]() $m$
odd, we can just as well compute
$m$
odd, we can just as well compute
![]() $\unicode[STIX]{x1D6FE}_{m}$
as the endomorphism of
$\unicode[STIX]{x1D6FE}_{m}$
as the endomorphism of
![]() $\mathbb{S}_{k}$
induced by the
$\mathbb{S}_{k}$
induced by the
![]() $\mathbb{P}^{1}$
-desuspension of
$\mathbb{P}^{1}$
-desuspension of
![]() $\operatorname{th}(\unicode[STIX]{x1D713}_{m,1}(x))$
(noting that
$\operatorname{th}(\unicode[STIX]{x1D713}_{m,1}(x))$
(noting that
![]() $\unicode[STIX]{x1D713}_{m}(x)$
is homogeneous)
$\unicode[STIX]{x1D713}_{m}(x)$
is homogeneous)
For
![]() $m$
even, we do the same, using
$m$
even, we do the same, using
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{m/2,2}(x)):\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
to compute
$\mathbb{P}(\unicode[STIX]{x1D713}_{m/2,2}(x)):\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
to compute
![]() $\unicode[STIX]{x1D6FE}_{m}$
$\unicode[STIX]{x1D6FE}_{m}$
We summarize the discussion as follows.
Lemma 6.5. Let
![]() $x$
be a
$x$
be a
![]() $k$
-point of
$k$
-point of
![]() $BN$
such that
$BN$
such that
![]() $x^{\ast }(\langle \bar{q}\rangle )=\langle -1\rangle =-1\in W(k)$
. For
$x^{\ast }(\langle \bar{q}\rangle )=\langle -1\rangle =-1\in W(k)$
. For
![]() $m$
odd, suppose we have chosen isomorphisms
$m$
odd, suppose we have chosen isomorphisms
![]() $\unicode[STIX]{x1D6FC}_{1}:\tilde{O} (1)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
$\unicode[STIX]{x1D6FC}_{1}:\tilde{O} (1)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such
$\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such
![]() $\operatorname{det}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D702}_{1}^{-1}=\operatorname{det}\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D702}_{m}^{-1}$
in
$\operatorname{det}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D702}_{1}^{-1}=\operatorname{det}\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D702}_{m}^{-1}$
in
![]() $k^{\times }/k^{\times 2}$
. Let
$k^{\times }/k^{\times 2}$
. Let
![]() $\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
$\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
![]() $[\mathbb{P}(\unicode[STIX]{x1D713}_{m,1}(x))]\in \text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
. Then
$[\mathbb{P}(\unicode[STIX]{x1D713}_{m,1}(x))]\in \text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
. Then
![]() $e(\tilde{O} (m))=\unicode[STIX]{x1D6FE}_{m}\cdot p_{1}^{\ast }e$
in
$e(\tilde{O} (m))=\unicode[STIX]{x1D6FE}_{m}\cdot p_{1}^{\ast }e$
in
![]() $H^{2}(BN,{\mathcal{W}})$
.
$H^{2}(BN,{\mathcal{W}})$
.
For
![]() $m$
even, suppose we have chosen isomorphisms
$m$
even, suppose we have chosen isomorphisms
![]() $\unicode[STIX]{x1D6FC}_{2}:\tilde{O} (2)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
$\unicode[STIX]{x1D6FC}_{2}:\tilde{O} (2)_{x}\rightarrow \mathbb{A}_{k}^{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such that the diagram (6.2) commutes up to multiplication by an element in
$\unicode[STIX]{x1D6FC}_{m}:\tilde{O} (m)_{x}\rightarrow \mathbb{A}_{k}^{2}$
such that the diagram (6.2) commutes up to multiplication by an element in
![]() $k^{\times 2}$
. Let
$k^{\times 2}$
. Let
![]() $\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
$\unicode[STIX]{x1D6FE}_{m}\in W(k)$
be the image of
![]() $[\mathbb{P}(\unicode[STIX]{x1D713}_{m/2,2}(x))]\in \text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
. Then
$[\mathbb{P}(\unicode[STIX]{x1D713}_{m/2,2}(x))]\in \text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
. Then
![]() $e(\tilde{O} (m))=\unicode[STIX]{x1D6FE}_{m}\cdot e(\tilde{O} (2))$
in
$e(\tilde{O} (m))=\unicode[STIX]{x1D6FE}_{m}\cdot e(\tilde{O} (2))$
in
![]() $H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
$H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))$
.
7 Descent, normalized bases and the computation of
 $\unicode[STIX]{x1D6FE}_{m}$
$\unicode[STIX]{x1D6FE}_{m}$
We find a suitable
![]() $x$
and compatible isomorphisms
$x$
and compatible isomorphisms
![]() $\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}$
,
![]() $\unicode[STIX]{x1D6FC}_{2}$
,
$\unicode[STIX]{x1D6FC}_{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{m}$
by using a descent description of the bundles
$\unicode[STIX]{x1D6FC}_{m}$
by using a descent description of the bundles
![]() $\tilde{O} (m)$
.
$\tilde{O} (m)$
.
We have
![]() $B_{0}N:=N\backslash \operatorname{GL}_{2}\subset BN$
, a
$B_{0}N:=N\backslash \operatorname{GL}_{2}\subset BN$
, a
![]() $\mathbb{G}_{m}$
-bundle over
$\mathbb{G}_{m}$
-bundle over
![]() $N_{T}(\text{GL}_{2})\backslash \operatorname{GL}_{2}=N\backslash \operatorname{SL}_{2}=\mathbb{P}^{2}-C$
. With respect to the projection
$N_{T}(\text{GL}_{2})\backslash \operatorname{GL}_{2}=N\backslash \operatorname{SL}_{2}=\mathbb{P}^{2}-C$
. With respect to the projection
![]() $BN\rightarrow \operatorname{BGL}_{2}$
,
$BN\rightarrow \operatorname{BGL}_{2}$
,
![]() $B_{0}N$
is the fiber over the base-point
$B_{0}N$
is the fiber over the base-point
![]() $0=\operatorname{GL}_{2}\backslash \operatorname{GL}_{2}\in \operatorname{BGL}_{2}$
.
$0=\operatorname{GL}_{2}\backslash \operatorname{GL}_{2}\in \operatorname{BGL}_{2}$
.
We describe the bundle
![]() $\tilde{O} (m)$
restricted to
$\tilde{O} (m)$
restricted to
![]() $B_{0}N$
in terms of descent data. Let
$B_{0}N$
in terms of descent data. Let
![]() $T(\operatorname{GL}_{2})\subset N_{T}(\operatorname{GL}_{2})$
be the standard torus in
$T(\operatorname{GL}_{2})\subset N_{T}(\operatorname{GL}_{2})$
be the standard torus in
![]() $\operatorname{GL}_{2}$
. The representation
$\operatorname{GL}_{2}$
. The representation
![]() $\unicode[STIX]{x1D70C}_{m}$
extends to the representation
$\unicode[STIX]{x1D70C}_{m}$
extends to the representation
with
![]() $\bar{\unicode[STIX]{x1D70C}}_{m}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70C}_{m}(\unicode[STIX]{x1D70E})$
and
$\bar{\unicode[STIX]{x1D70C}}_{m}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D70C}_{m}(\unicode[STIX]{x1D70E})$
and
Thus
![]() $\tilde{O} (m)$
restricted to
$\tilde{O} (m)$
restricted to
![]() $B_{0}N$
is the pullback of the bundle
$B_{0}N$
is the pullback of the bundle
![]() $\bar{O}(m)$
on
$\bar{O}(m)$
on
![]() $N_{T}\backslash \operatorname{GL}_{2}=\mathbb{P}^{2}-C$
defined by the representation
$N_{T}\backslash \operatorname{GL}_{2}=\mathbb{P}^{2}-C$
defined by the representation
![]() $\bar{\unicode[STIX]{x1D70C}}_{m}$
, via the quotient map
$\bar{\unicode[STIX]{x1D70C}}_{m}$
, via the quotient map
![]() $N\backslash \operatorname{GL}_{2}\rightarrow N_{T}\backslash \operatorname{GL}_{2}$
.
$N\backslash \operatorname{GL}_{2}\rightarrow N_{T}\backslash \operatorname{GL}_{2}$
.
We let
![]() $k(i):=k[T]/(T^{2}+1)$
, giving us the separable
$k(i):=k[T]/(T^{2}+1)$
, giving us the separable
![]() $k$
-algebra with automorphism
$k$
-algebra with automorphism
![]() $c:k(i)\rightarrow k(i)$
,
$c:k(i)\rightarrow k(i)$
,
![]() $c(i)=-i$
, over
$c(i)=-i$
, over
![]() $k$
. For
$k$
. For
![]() $z=a+bi\in k(i)$
,
$z=a+bi\in k(i)$
,
![]() $a,b\in k$
, we write
$a,b\in k$
, we write
![]() $a=\operatorname{Re}z$
,
$a=\operatorname{Re}z$
,
![]() $b=\operatorname{Im}z$
and extend this notation in the obvious way to the polynomial ring
$b=\operatorname{Im}z$
and extend this notation in the obvious way to the polynomial ring
![]() $k(i)[X_{0},\ldots ,X_{r}]$
.
$k(i)[X_{0},\ldots ,X_{r}]$
.
We take a pair of
![]() $k(i)$
-points
$k(i)$
-points
![]() $y_{1},y_{2}\in \mathbb{A}^{2}(k(i))$
, linearly independent over
$y_{1},y_{2}\in \mathbb{A}^{2}(k(i))$
, linearly independent over
![]() $k(i)$
, such that
$k(i)$
, such that
This gives us the
![]() $k$
-point
$k$
-point
![]() $x\in N\backslash \operatorname{GL}_{2}=B_{0}N$
. Then a
$x\in N\backslash \operatorname{GL}_{2}=B_{0}N$
. Then a
![]() $k(i)$
-basis
$k(i)$
-basis
![]() $v_{1,m},v_{2,m}$
of
$v_{1,m},v_{2,m}$
of
![]() $F(m)\otimes k(i)=k(i)^{2}$
descends to a
$F(m)\otimes k(i)=k(i)^{2}$
descends to a
![]() $k$
-basis of
$k$
-basis of
![]() $\tilde{O} (m)_{x}$
if the equation
$\tilde{O} (m)_{x}$
if the equation
is satisfied.
To complete the computation of
![]() $e(\tilde{O} (m))$
, we have
$e(\tilde{O} (m))$
, we have
Theorem 7.1. Suppose
![]() $k$
is a field of characteristic zero, or of characteristic
$k$
is a field of characteristic zero, or of characteristic
![]() $\ell >2$
, with
$\ell >2$
, with
![]() $(\ell ,m)=1$
. For
$(\ell ,m)=1$
. For
![]() $m$
odd, define
$m$
odd, define
![]() $\unicode[STIX]{x1D716}(m)=+1$
for
$\unicode[STIX]{x1D716}(m)=+1$
for
![]() $m\equiv 1\,\text{mod}\,4$
,
$m\equiv 1\,\text{mod}\,4$
,
![]() $\unicode[STIX]{x1D716}(m)=-1$
for
$\unicode[STIX]{x1D716}(m)=-1$
for
![]() $m\equiv 3\,\text{mod}\,4$
. Then
$m\equiv 3\,\text{mod}\,4$
. Then
 $$\begin{eqnarray}e(\tilde{O} (m))=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}(m)\cdot m\cdot p^{\ast }e\in H^{2}(BN,{\mathcal{W}})\quad & \text{ for }m\text{ odd},\\ {\displaystyle \frac{m}{2}}\cdot \tilde{e}\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))\quad & \text{ for }m\equiv 2\,\text{mod}\,4,\\ -{\displaystyle \frac{m}{2}}\cdot \tilde{e}\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))\quad & \text{ for }m\equiv 0\,\text{mod}\,4.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}e(\tilde{O} (m))=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}(m)\cdot m\cdot p^{\ast }e\in H^{2}(BN,{\mathcal{W}})\quad & \text{ for }m\text{ odd},\\ {\displaystyle \frac{m}{2}}\cdot \tilde{e}\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))\quad & \text{ for }m\equiv 2\,\text{mod}\,4,\\ -{\displaystyle \frac{m}{2}}\cdot \tilde{e}\in H^{2}(BN,{\mathcal{W}}(\unicode[STIX]{x1D6FE}))\quad & \text{ for }m\equiv 0\,\text{mod}\,4.\end{array}\right.\end{eqnarray}$$
Moreover,
![]() $\tilde{e}^{2}=4p^{\ast }e^{2}$
in
$\tilde{e}^{2}=4p^{\ast }e^{2}$
in
![]() $H^{4}(BN,{\mathcal{W}})$
and
$H^{4}(BN,{\mathcal{W}})$
and
![]() $e(\tilde{O} ^{-}(m))=-e(\tilde{O} (m))$
.
$e(\tilde{O} ^{-}(m))=-e(\tilde{O} (m))$
.
Proof. Noting that
![]() $(x,y)\mapsto (-x,y)$
defines an isomorphism of
$(x,y)\mapsto (-x,y)$
defines an isomorphism of
![]() $\unicode[STIX]{x1D70C}_{m}$
with
$\unicode[STIX]{x1D70C}_{m}$
with
![]() $\unicode[STIX]{x1D70C}_{m}^{-}$
(as right representations) and induces
$\unicode[STIX]{x1D70C}_{m}^{-}$
(as right representations) and induces
![]() $(-1)$
on the determinant, the assertion for
$(-1)$
on the determinant, the assertion for
![]() $e(\tilde{O} ^{-}(m))$
follows.
$e(\tilde{O} ^{-}(m))$
follows.
The proof relies on the approach set forth in Lemma 6.5. We find a suitable
![]() $k$
-point
$k$
-point
![]() $x$
of
$x$
of
![]() $B_{0}N$
and compatible trivializations
$B_{0}N$
and compatible trivializations
![]() $\unicode[STIX]{x1D6FC}_{m}$
, compute the maps
$\unicode[STIX]{x1D6FC}_{m}$
, compute the maps
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})$
and use these to compute the factor
$\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})$
and use these to compute the factor
![]() $\unicode[STIX]{x1D6FE}_{m}$
.
$\unicode[STIX]{x1D6FE}_{m}$
.
We begin by finding a
![]() $k$
-point
$k$
-point
![]() $x\in B_{0}N=N\backslash \operatorname{GL}_{2}$
lying over the point
$x\in B_{0}N=N\backslash \operatorname{GL}_{2}$
lying over the point
![]() $[1:0:1]\in N_{T}(\operatorname{GL}_{2})\backslash \operatorname{GL}_{2}=\mathbb{P}^{2}-C$
with
$[1:0:1]\in N_{T}(\operatorname{GL}_{2})\backslash \operatorname{GL}_{2}=\mathbb{P}^{2}-C$
with
![]() $Q(x)=-1\,\text{mod}\,k^{\times 2}$
.
$Q(x)=-1\,\text{mod}\,k^{\times 2}$
.
We have the double cover
![]() $T(\operatorname{SL}_{2})\backslash \operatorname{SL}_{2}\rightarrow N\backslash \operatorname{SL}_{2}$
, that is,
$T(\operatorname{SL}_{2})\backslash \operatorname{SL}_{2}\rightarrow N\backslash \operatorname{SL}_{2}$
, that is,
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}^{2}-C$
, and the pair of conjugate points
$\mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}\rightarrow \mathbb{P}^{2}-C$
, and the pair of conjugate points
![]() $y,\bar{y}\in \mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
lying over
$y,\bar{y}\in \mathbb{P}^{1}\times \mathbb{P}^{1}-\unicode[STIX]{x1D6E5}$
lying over
![]() $[1:0:1]$
. As the map
$[1:0:1]$
. As the map
![]() $\unicode[STIX]{x1D70B}:\mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{2}$
is given by
$\unicode[STIX]{x1D70B}:\mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{2}$
is given by
we compute the conjugate points
![]() $y,\bar{y}$
as
$y,\bar{y}$
as
We lift
![]() $y,\bar{y}$
to the pair
$y,\bar{y}$
to the pair
![]() $y_{1}=(1,-i)$
,
$y_{1}=(1,-i)$
,
![]() $y_{2}=(-i,1)$
$y_{2}=(-i,1)$
![]() $y_{1},y_{2}\in k(i)^{2}$
, giving the matrix
$y_{1},y_{2}\in k(i)^{2}$
, giving the matrix
with determinant 2. The pair
![]() $y_{1},y_{2}$
defines a
$y_{1},y_{2}$
defines a
![]() $k$
-point
$k$
-point
![]() $x$
of
$x$
of
![]() $B_{0}N=N\backslash \operatorname{GL}_{2}$
lying over
$B_{0}N=N\backslash \operatorname{GL}_{2}$
lying over
![]() $(1:0:1)\in N_{T}\backslash \operatorname{GL}_{2}$
, since
$(1:0:1)\in N_{T}\backslash \operatorname{GL}_{2}$
, since
Identifying the fiber
![]() $\tilde{O} (m)_{x^{\ast }}$
with
$\tilde{O} (m)_{x^{\ast }}$
with
![]() $F(m)\times x^{\ast }=k(i)^{2}$
, we have the standard basis
$F(m)\times x^{\ast }=k(i)^{2}$
, we have the standard basis
![]() $e_{1}=(1,0)$
,
$e_{1}=(1,0)$
,
![]() $e_{2}=(0,1)$
for
$e_{2}=(0,1)$
for
![]() $\tilde{O} (m)_{x^{\ast }}$
. We first consider the case of odd
$\tilde{O} (m)_{x^{\ast }}$
. We first consider the case of odd
![]() $m$
.
$m$
.
For
![]() $m\equiv 1\,\text{mod}\,4$
, define
$m\equiv 1\,\text{mod}\,4$
, define
![]() $v_{1,m}=(1,i)$
,
$v_{1,m}=(1,i)$
,
![]() $v_{2,m}=(i,1)$
. We have
$v_{2,m}=(i,1)$
. We have
so
![]() $v_{1,m},v_{2,m}$
satisfy the descent equation (7.1) and thus descend to a
$v_{1,m},v_{2,m}$
satisfy the descent equation (7.1) and thus descend to a
![]() $k$
-basis of
$k$
-basis of
![]() $\tilde{O} (m)_{x}$
with determinant
$\tilde{O} (m)_{x}$
with determinant
![]() $2\cdot e_{1}\wedge e_{2}$
.
$2\cdot e_{1}\wedge e_{2}$
.
For
![]() $m\equiv 3\,\text{mod}\,4$
, define
$m\equiv 3\,\text{mod}\,4$
, define
![]() $v_{1,m}=(1,-i)$
,
$v_{1,m}=(1,-i)$
,
![]() $v_{2,m}=(-i,1)$
, and we have as above
$v_{2,m}=(-i,1)$
, and we have as above
The
![]() $k$
-basis
$k$
-basis
![]() $v_{1,m},v_{2,m}$
also has determinant
$v_{1,m},v_{2,m}$
also has determinant
![]() $2\cdot e_{1}\wedge e_{2}$
.
$2\cdot e_{1}\wedge e_{2}$
.
We remark that in all cases of odd
![]() $m$
, our basis has determinant
$m$
, our basis has determinant
![]() $2\cdot e_{1}\wedge e_{2}$
, in particular
$2\cdot e_{1}\wedge e_{2}$
, in particular
For
![]() $m\equiv 2\,\text{mod}\,4$
, define
$m\equiv 2\,\text{mod}\,4$
, define
![]() $v_{1,m}=(1,-1)$
,
$v_{1,m}=(1,-1)$
,
![]() $v_{2,m}=(i,i)$
. Then
$v_{2,m}=(i,i)$
. Then
The basis
![]() $v_{1,m},v_{2,m}$
has determinant
$v_{1,m},v_{2,m}$
has determinant
![]() $2i\cdot e_{1}\wedge e_{2}$
, but in the case of even
$2i\cdot e_{1}\wedge e_{2}$
, but in the case of even
![]() $m$
, the representation
$m$
, the representation
![]() $\unicode[STIX]{x1D70C}_{m}$
does not land in
$\unicode[STIX]{x1D70C}_{m}$
does not land in
![]() $\operatorname{SL}_{2}$
, and thus the determinant bundle
$\operatorname{SL}_{2}$
, and thus the determinant bundle
![]() $\operatorname{det}\tilde{O} (2)$
is the 2-torsion generator
$\operatorname{det}\tilde{O} (2)$
is the 2-torsion generator
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\text{Pic}(N\backslash \operatorname{GL}_{2})$
, corresponding to the character
$\text{Pic}(N\backslash \operatorname{GL}_{2})$
, corresponding to the character
![]() $\unicode[STIX]{x1D70C}(0)^{-}$
of
$\unicode[STIX]{x1D70C}(0)^{-}$
of
![]() $N$
. In any case,
$N$
. In any case,
![]() $v_{1,m}\wedge v_{2,m}$
gives a generator for
$v_{1,m}\wedge v_{2,m}$
gives a generator for
![]() $\operatorname{det}\tilde{O} (2)_{x}$
.
$\operatorname{det}\tilde{O} (2)_{x}$
.
For
![]() $m\equiv 0\,\text{mod}\,4$
, we use the basis
$m\equiv 0\,\text{mod}\,4$
, we use the basis
![]() $v_{1,m}=(1,1)$
,
$v_{1,m}=(1,1)$
,
![]() $v_{2,m}=(-i,i)$
for
$v_{2,m}=(-i,i)$
for
![]() $\tilde{O} (m)_{x}$
, which satisfies the descent equation
$\tilde{O} (m)_{x}$
, which satisfies the descent equation
and has the determinant
![]() $2i\cdot e_{1}\wedge e_{2}$
.
$2i\cdot e_{1}\wedge e_{2}$
.
For all
![]() $m$
even, we have
$m$
even, we have
The multiplication map
![]() $\unicode[STIX]{x1D713}_{m,a}:\tilde{O} (a)_{\tilde{x}}\rightarrow \tilde{O} (am)_{\tilde{x}}$
is given by
$\unicode[STIX]{x1D713}_{m,a}:\tilde{O} (a)_{\tilde{x}}\rightarrow \tilde{O} (am)_{\tilde{x}}$
is given by
We express
![]() $\unicode[STIX]{x1D713}_{m}$
with respect our bases for
$\unicode[STIX]{x1D713}_{m}$
with respect our bases for
![]() $\tilde{O} (a)_{x}$
and
$\tilde{O} (a)_{x}$
and
![]() $\tilde{O} (am)_{x}$
.
$\tilde{O} (am)_{x}$
.
For
![]() $a,m\equiv 1\,\text{mod}\,4$
, we have
$a,m\equiv 1\,\text{mod}\,4$
, we have
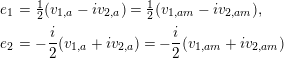 $$\begin{eqnarray}\displaystyle e_{1} & = & \displaystyle {\textstyle \frac{1}{2}}(v_{1,a}-iv_{2,a})={\textstyle \frac{1}{2}}(v_{1,am}-iv_{2,am}),\nonumber\\ \displaystyle e_{2} & = & \displaystyle -\frac{i}{2}(v_{1,a}+iv_{2,a})=-\frac{i}{2}(v_{1,am}+iv_{2,am})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{1} & = & \displaystyle {\textstyle \frac{1}{2}}(v_{1,a}-iv_{2,a})={\textstyle \frac{1}{2}}(v_{1,am}-iv_{2,am}),\nonumber\\ \displaystyle e_{2} & = & \displaystyle -\frac{i}{2}(v_{1,a}+iv_{2,a})=-\frac{i}{2}(v_{1,am}+iv_{2,am})\nonumber\end{eqnarray}$$
and
![]() $\unicode[STIX]{x1D713}_{m,a}$
is given by
$\unicode[STIX]{x1D713}_{m,a}$
is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a}) & = & \displaystyle \unicode[STIX]{x1D713}_{m,a}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{m}e_{1}+i(x_{0}-ix_{1})^{m}e_{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}((x_{0}+ix_{1})^{m}+(x_{0}-ix_{1})^{m})v_{1,am}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{i}{2}((x_{0}+ix_{1})^{m}-(x_{0}-ix_{i})^{m})v_{2,am}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}+ix_{1})^{m}\cdot v_{1,m}+\operatorname{Im}(x_{0}+ix_{1})^{m}\cdot v_{2,am}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a}) & = & \displaystyle \unicode[STIX]{x1D713}_{m,a}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{m}e_{1}+i(x_{0}-ix_{1})^{m}e_{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}((x_{0}+ix_{1})^{m}+(x_{0}-ix_{1})^{m})v_{1,am}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{i}{2}((x_{0}+ix_{1})^{m}-(x_{0}-ix_{i})^{m})v_{2,am}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}+ix_{1})^{m}\cdot v_{1,m}+\operatorname{Im}(x_{0}+ix_{1})^{m}\cdot v_{2,am}.\nonumber\end{eqnarray}$$
For
![]() $m\equiv 3\,\text{mod}\,4$
,
$m\equiv 3\,\text{mod}\,4$
,
![]() $a\equiv 1\,\text{mod}\,4$
, we have
$a\equiv 1\,\text{mod}\,4$
, we have
and
![]() $\unicode[STIX]{x1D713}_{m,a}$
is given by
$\unicode[STIX]{x1D713}_{m,a}$
is given by
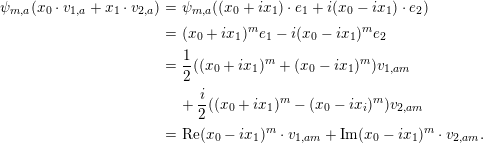 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a}) & = & \displaystyle \unicode[STIX]{x1D713}_{m,a}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{m}e_{1}-i(x_{0}-ix_{1})^{m}e_{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}((x_{0}+ix_{1})^{m}+(x_{0}-ix_{1})^{m})v_{1,am}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{i}{2}((x_{0}+ix_{1})^{m}-(x_{0}-ix_{i})^{m})v_{2,am}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}-ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}-ix_{1})^{m}\cdot v_{2,am}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a}) & = & \displaystyle \unicode[STIX]{x1D713}_{m,a}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{m}e_{1}-i(x_{0}-ix_{1})^{m}e_{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}((x_{0}+ix_{1})^{m}+(x_{0}-ix_{1})^{m})v_{1,am}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{i}{2}((x_{0}+ix_{1})^{m}-(x_{0}-ix_{i})^{m})v_{2,am}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}-ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}-ix_{1})^{m}\cdot v_{2,am}.\nonumber\end{eqnarray}$$
For
![]() $a\equiv 3\,\text{mod}\,4$
, we arrive at the same formulas, giving in the end the formulas for all odd
$a\equiv 3\,\text{mod}\,4$
, we arrive at the same formulas, giving in the end the formulas for all odd
![]() $a$
$a$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a})\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}\operatorname{Re}(x_{0}+ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}+ix_{1})^{m}\cdot v_{2,am}\quad & \text{ for }m\equiv 1\,\text{mod}\,4,\\ \operatorname{Re}(x_{0}-ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}-ix_{1})^{m}\cdot v_{2,am}\quad & \text{ for }m\equiv 3\,\text{mod}\,4.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D713}_{m,a}(x_{0}\cdot v_{1,a}+x_{1}\cdot v_{2,a})\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}\operatorname{Re}(x_{0}+ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}+ix_{1})^{m}\cdot v_{2,am}\quad & \text{ for }m\equiv 1\,\text{mod}\,4,\\ \operatorname{Re}(x_{0}-ix_{1})^{m}\cdot v_{1,am}+\operatorname{Im}(x_{0}-ix_{1})^{m}\cdot v_{2,am}\quad & \text{ for }m\equiv 3\,\text{mod}\,4.\end{array}\right.\nonumber\end{eqnarray}$$
For even
![]() $m$
, we write
$m$
, we write
![]() $m=2^{r}n$
with
$m=2^{r}n$
with
![]() $n$
odd and write
$n$
odd and write
![]() $\unicode[STIX]{x1D713}_{m/2,2a}:\tilde{O} (2a)\rightarrow \tilde{O} (am)$
as the composition
$\unicode[STIX]{x1D713}_{m/2,2a}:\tilde{O} (2a)\rightarrow \tilde{O} (am)$
as the composition
A computation as above yields
For
![]() $\unicode[STIX]{x1D713}_{2,2^{s}an}$
there are two cases: we take
$\unicode[STIX]{x1D713}_{2,2^{s}an}$
there are two cases: we take
![]() $a$
odd. Then
$a$
odd. Then
and for all
![]() $s\geqslant 2$
$s\geqslant 2$
This second formula also takes care of the case of even
![]() $a$
.
$a$
.
Finally, we need to consider the map
![]() $\unicode[STIX]{x1D713}_{2,1}:\tilde{O} (1)\rightarrow \tilde{O} (2)$
. We have
$\unicode[STIX]{x1D713}_{2,1}:\tilde{O} (1)\rightarrow \tilde{O} (2)$
. We have
and
![]() $\unicode[STIX]{x1D713}_{2,1}$
is given by
$\unicode[STIX]{x1D713}_{2,1}$
is given by
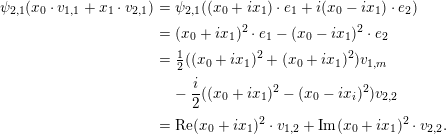 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{2,1}(x_{0}\cdot v_{1,1}+x_{1}\cdot v_{2,1}) & = & \displaystyle \unicode[STIX]{x1D713}_{2,1}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{2}\cdot e_{1}-(x_{0}-ix_{1})^{2}\cdot e_{2}\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}((x_{0}+ix_{1})^{2}+(x_{0}+ix_{1})^{2})v_{1,m}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{i}{2}((x_{0}+ix_{1})^{2}-(x_{0}-ix_{i})^{2})v_{2,2}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}+ix_{1})^{2}\cdot v_{1,2}+\operatorname{Im}(x_{0}+ix_{1})^{2}\cdot v_{2,2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{2,1}(x_{0}\cdot v_{1,1}+x_{1}\cdot v_{2,1}) & = & \displaystyle \unicode[STIX]{x1D713}_{2,1}((x_{0}+ix_{1})\cdot e_{1}+i(x_{0}-ix_{1})\cdot e_{2})\nonumber\\ \displaystyle & = & \displaystyle (x_{0}+ix_{1})^{2}\cdot e_{1}-(x_{0}-ix_{1})^{2}\cdot e_{2}\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}((x_{0}+ix_{1})^{2}+(x_{0}+ix_{1})^{2})v_{1,m}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{i}{2}((x_{0}+ix_{1})^{2}-(x_{0}-ix_{i})^{2})v_{2,2}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Re}(x_{0}+ix_{1})^{2}\cdot v_{1,2}+\operatorname{Im}(x_{0}+ix_{1})^{2}\cdot v_{2,2}.\nonumber\end{eqnarray}$$
Thus, as an endomorphism of
![]() $\mathbb{P}^{1}$
, we have the expression for
$\mathbb{P}^{1}$
, we have the expression for
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})$
:
$\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})$
:
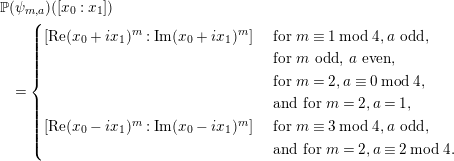 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}(\unicode[STIX]{x1D713}_{m,a})([x_{0}:x_{1}])\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\hspace{0.0pt}[\operatorname{Re}(x_{0}+ix_{1})^{m}:\operatorname{Im}(x_{0}+ix_{1})^{m}]\quad & \text{ for }m\equiv 1\,\text{mod}\,4,a\text{ odd},\\ \quad & \text{ for }m\text{ odd, }a\text{ even},\\ \quad & \text{ for }m=2,a\equiv 0\,\text{mod}\,4,\\ \quad & \text{ and for }m=2,a=1,\\ \hspace{0.0pt}[\operatorname{Re}(x_{0}-ix_{1})^{m}:\operatorname{Im}(x_{0}-ix_{1})^{m}]\quad & \text{ for }m\equiv 3\,\text{mod}\,4,a\text{ odd},\\ \quad & \text{ and for }m=2,a\equiv 2\,\text{mod}\,4.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}(\unicode[STIX]{x1D713}_{m,a})([x_{0}:x_{1}])\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\hspace{0.0pt}[\operatorname{Re}(x_{0}+ix_{1})^{m}:\operatorname{Im}(x_{0}+ix_{1})^{m}]\quad & \text{ for }m\equiv 1\,\text{mod}\,4,a\text{ odd},\\ \quad & \text{ for }m\text{ odd, }a\text{ even},\\ \quad & \text{ for }m=2,a\equiv 0\,\text{mod}\,4,\\ \quad & \text{ and for }m=2,a=1,\\ \hspace{0.0pt}[\operatorname{Re}(x_{0}-ix_{1})^{m}:\operatorname{Im}(x_{0}-ix_{1})^{m}]\quad & \text{ for }m\equiv 3\,\text{mod}\,4,a\text{ odd},\\ \quad & \text{ and for }m=2,a\equiv 2\,\text{mod}\,4.\end{array}\right.\nonumber\end{eqnarray}$$
In all cases except for
![]() $\unicode[STIX]{x1D713}_{2,1}:\tilde{O} (1)\rightarrow \tilde{O} (2)$
, the “relative determinants” are 1 in
$\unicode[STIX]{x1D713}_{2,1}:\tilde{O} (1)\rightarrow \tilde{O} (2)$
, the “relative determinants” are 1 in
![]() $W(k)$
.
$W(k)$
.
To complete the computation, we use Lemma 7.2 below to determine the
![]() $\mathbb{A}^{1}$
-degree
$\mathbb{A}^{1}$
-degree
![]() $[\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})]\in W(k)$
of
$[\mathbb{P}(\unicode[STIX]{x1D713}_{m,a})]\in W(k)$
of
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{m,a}):\mathbb{P}_{\mathbb{Q}}^{1}\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$
in cases described above. Combined with our table above, that lemma gives, for
$\mathbb{P}(\unicode[STIX]{x1D713}_{m,a}):\mathbb{P}_{\mathbb{Q}}^{1}\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$
in cases described above. Combined with our table above, that lemma gives, for
![]() $p$
a prime,
$p$
a prime,
 $$\begin{eqnarray}[\mathbb{P}(\unicode[STIX]{x1D713}_{p,a})]=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}(p)\cdot p\langle 1\rangle \quad & \text{for }p\text{ odd and }a\text{ odd},\\ p\langle 1\rangle \quad & \text{for }p\text{ odd and }a\text{ even},\\ 2\langle 1\rangle \quad & \text{for }p=2,a\equiv 0\,\text{mod}\,4,\\ -2\langle 1\rangle \quad & \text{for }p=2,a\equiv 2\,\text{mod}\,4\\ 2\langle 1\rangle \quad & \text{for }p=2,a=1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}[\mathbb{P}(\unicode[STIX]{x1D713}_{p,a})]=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}(p)\cdot p\langle 1\rangle \quad & \text{for }p\text{ odd and }a\text{ odd},\\ p\langle 1\rangle \quad & \text{for }p\text{ odd and }a\text{ even},\\ 2\langle 1\rangle \quad & \text{for }p=2,a\equiv 0\,\text{mod}\,4,\\ -2\langle 1\rangle \quad & \text{for }p=2,a\equiv 2\,\text{mod}\,4\\ 2\langle 1\rangle \quad & \text{for }p=2,a=1.\end{array}\right.\end{eqnarray}$$
This computation of the
![]() $\mathbb{A}^{1}$
-degree of
$\mathbb{A}^{1}$
-degree of
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{p,a})$
together with Lemma 6.5 yields the computation of
$\mathbb{P}(\unicode[STIX]{x1D713}_{p,a})$
together with Lemma 6.5 yields the computation of
![]() $e(\tilde{O} (m))$
as asserted in Theorem 7.1: in the case of odd
$e(\tilde{O} (m))$
as asserted in Theorem 7.1: in the case of odd
![]() $m$
, we write
$m$
, we write
![]() $m=\prod _{i=1}^{r}p_{i}$
with the
$m=\prod _{i=1}^{r}p_{i}$
with the
![]() $p_{i}$
odd primes, let
$p_{i}$
odd primes, let
![]() $a_{i}=\prod _{j=1}^{i-1}p_{i}$
and write
$a_{i}=\prod _{j=1}^{i-1}p_{i}$
and write
![]() $\unicode[STIX]{x1D713}_{m,1}=\unicode[STIX]{x1D713}_{p_{r},a_{r}}\circ \cdots \circ \unicode[STIX]{x1D713}_{p_{1},1}$
. This gives
$\unicode[STIX]{x1D713}_{m,1}=\unicode[STIX]{x1D713}_{p_{r},a_{r}}\circ \cdots \circ \unicode[STIX]{x1D713}_{p_{1},1}$
. This gives
![]() $e(\tilde{O} (m))=\prod _{i=1}^{r}\unicode[STIX]{x1D716}(p_{i})\cdot p_{i}\cdot p^{\ast }e=\unicode[STIX]{x1D716}(m)\cdot m\cdot p^{\ast }e$
. For
$e(\tilde{O} (m))=\prod _{i=1}^{r}\unicode[STIX]{x1D716}(p_{i})\cdot p_{i}\cdot p^{\ast }e=\unicode[STIX]{x1D716}(m)\cdot m\cdot p^{\ast }e$
. For
![]() $m=2^{r}\cdot n$
with
$m=2^{r}\cdot n$
with
![]() $n$
odd, we write
$n$
odd, we write
![]() $\unicode[STIX]{x1D713}_{m/2,2}=\unicode[STIX]{x1D713}_{2,m/2}\circ \cdots \circ \unicode[STIX]{x1D713}_{2,2n}\circ \unicode[STIX]{x1D713}_{n,2}$
, which, computing
$\unicode[STIX]{x1D713}_{m/2,2}=\unicode[STIX]{x1D713}_{2,m/2}\circ \cdots \circ \unicode[STIX]{x1D713}_{2,2n}\circ \unicode[STIX]{x1D713}_{n,2}$
, which, computing
![]() $[\mathbb{P}(\unicode[STIX]{x1D713}_{n,2})]$
as above, gives
$[\mathbb{P}(\unicode[STIX]{x1D713}_{n,2})]$
as above, gives
![]() $e(\tilde{O} (m))=\pm 2^{r-1}n\cdot e(\tilde{O} (2))$
, with the sign
$e(\tilde{O} (m))=\pm 2^{r-1}n\cdot e(\tilde{O} (2))$
, with the sign
![]() $+$
for
$+$
for
![]() $r=1$
,
$r=1$
,
![]() $-$
for
$-$
for
![]() $r>1$
.
$r>1$
.
We complete the proof by showing
![]() $e(\tilde{O} (2))^{2}=4e(\tilde{O} (1))^{2}$
in
$e(\tilde{O} (2))^{2}=4e(\tilde{O} (1))^{2}$
in
![]() $H^{4}(BN,{\mathcal{W}})$
. The bundle
$H^{4}(BN,{\mathcal{W}})$
. The bundle
![]() $\tilde{O} (2)\oplus \tilde{O} (2)$
is the bundle associated to the representation
$\tilde{O} (2)\oplus \tilde{O} (2)$
is the bundle associated to the representation
As
![]() $\operatorname{det}^{-2}(\tilde{O} (2))$
is the line bundle associated to the representation
$\operatorname{det}^{-2}(\tilde{O} (2))$
is the line bundle associated to the representation
![]() $(\unicode[STIX]{x1D70C}_{0}^{-})^{2}=\unicode[STIX]{x1D70C}_{0}$
, we have a canonical isomorphism
$(\unicode[STIX]{x1D70C}_{0}^{-})^{2}=\unicode[STIX]{x1D70C}_{0}$
, we have a canonical isomorphism
![]() $\operatorname{det}^{-2}(\tilde{O} (2))\cong O_{BN}$
, and via the induced identification of
$\operatorname{det}^{-2}(\tilde{O} (2))\cong O_{BN}$
, and via the induced identification of
![]() $H^{4} (\!BN,{\mathcal{W}}(\operatorname{det}^{-2}(\tilde{O} (2)))\cong H^{4}(BN,{\mathcal{W}})$
, we have
$H^{4} (\!BN,{\mathcal{W}}(\operatorname{det}^{-2}(\tilde{O} (2)))\cong H^{4}(BN,{\mathcal{W}})$
, we have
![]() $e(\tilde{O} (2))^{2}=e(\tilde{O} (2)\oplus \tilde{O} (2))$
. We have the multiplication map
$e(\tilde{O} (2))^{2}=e(\tilde{O} (2)\oplus \tilde{O} (2))$
. We have the multiplication map
Using the bases
![]() $(v_{1,1},0)$
,
$(v_{1,1},0)$
,
![]() $(v_{2,1},0)$
,
$(v_{2,1},0)$
,
![]() $(0,v_{1,1})$
,
$(0,v_{1,1})$
,
![]() $(0,v_{2,1})$
for
$(0,v_{2,1})$
for
![]() $(\tilde{O} (1)\oplus \tilde{O} (1))_{x}$
and
$(\tilde{O} (1)\oplus \tilde{O} (1))_{x}$
and
![]() $(v_{1,2},0)$
,
$(v_{1,2},0)$
,
![]() $(v_{2,2},0)$
,
$(v_{2,2},0)$
,
![]() $(0,v_{1,2})$
,
$(0,v_{1,2})$
,
![]() $(0,v_{2,2})$
for
$(0,v_{2,2})$
for
![]() $(\tilde{O} (2)\oplus \tilde{O} (2))_{x}$
, we have the respective determinants
$(\tilde{O} (2)\oplus \tilde{O} (2))_{x}$
, we have the respective determinants
![]() $4$
and
$4$
and
![]() $-4$
times the generator
$-4$
times the generator
![]() $(e_{1},0)\wedge (e_{2},0)\wedge (0,e_{1})\wedge (0,e_{2})$
, that is, a relative determinant of
$(e_{1},0)\wedge (e_{2},0)\wedge (0,e_{1})\wedge (0,e_{2})$
, that is, a relative determinant of
![]() $-1$
. Note that
$-1$
. Note that
![]() $e(\tilde{O} (2))$
lives in
$e(\tilde{O} (2))$
lives in
![]() $H^{2}(BN,{\mathcal{W}}(\operatorname{det}^{-1}\tilde{O} (2)))$
, and to put
$H^{2}(BN,{\mathcal{W}}(\operatorname{det}^{-1}\tilde{O} (2)))$
, and to put
![]() $e(\tilde{O} (2))^{2}\in H^{4}(BN,{\mathcal{W}}(\operatorname{det}^{-2}\tilde{O} (2)))$
into
$e(\tilde{O} (2))^{2}\in H^{4}(BN,{\mathcal{W}}(\operatorname{det}^{-2}\tilde{O} (2)))$
into
![]() $H^{4}(BN,{\mathcal{W}})$
we need to multiply with the square of a local generator for
$H^{4}(BN,{\mathcal{W}})$
we need to multiply with the square of a local generator for
![]() $\operatorname{det}\tilde{O} (2)$
to give the isomorphism
$\operatorname{det}\tilde{O} (2)$
to give the isomorphism
![]() ${\mathcal{W}}(\operatorname{det}^{-2}\tilde{O} (2))\rightarrow {\mathcal{W}}$
. At the point
${\mathcal{W}}(\operatorname{det}^{-2}\tilde{O} (2))\rightarrow {\mathcal{W}}$
. At the point
![]() $x$
, a local generator is
$x$
, a local generator is
![]() $v_{1,2}\wedge v_{2,2}=2ie_{1}\wedge e_{2}$
, so multiplying by
$v_{1,2}\wedge v_{2,2}=2ie_{1}\wedge e_{2}$
, so multiplying by
![]() $(v_{1,2}\wedge v_{2,2})^{2}$
introduces the additional factor
$(v_{1,2}\wedge v_{2,2})^{2}$
introduces the additional factor
![]() $\langle -4\rangle =-1$
into the computation. Putting this all together, we see that the
$\langle -4\rangle =-1$
into the computation. Putting this all together, we see that the
![]() $\mathbb{A}^{1}$
degree of
$\mathbb{A}^{1}$
degree of
computes
![]() $e(\tilde{O} (2))^{2}$
. As
$e(\tilde{O} (2))^{2}$
. As
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{2,1})$
has
$\mathbb{P}(\unicode[STIX]{x1D713}_{2,1})$
has
![]() $\mathbb{A}^{1}$
-degree
$\mathbb{A}^{1}$
-degree
![]() $2\langle 1\rangle$
, this gives
$2\langle 1\rangle$
, this gives
![]() $e(\tilde{O} (2))^{2}=4p^{\ast }e^{2}$
.
$e(\tilde{O} (2))^{2}=4p^{\ast }e^{2}$
.
We finish this section with proofs of results we have used in the proof of Theorem 7.1.
Lemma 7.2. Let
![]() $k$
be a perfect field and let
$k$
be a perfect field and let
![]() $m$
be an integer. Consider the maps
$m$
be an integer. Consider the maps
![]() $G_{m\pm }:\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
$G_{m\pm }:\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
(a)
 $G_{m+}([x_{0}:x_{1}])=[\operatorname{Re}(x_{0}+ix_{1})^{m}:\operatorname{Im}(x_{0}+ix_{1})^{m}]$
$G_{m+}([x_{0}:x_{1}])=[\operatorname{Re}(x_{0}+ix_{1})^{m}:\operatorname{Im}(x_{0}+ix_{1})^{m}]$
(b)
 $G_{m-}([x_{0}:x_{1}])=[\operatorname{Re}(x_{0}-ix_{1})^{m}:\operatorname{Im}(x_{0}-ix_{1})^{m}]$
,
$G_{m-}([x_{0}:x_{1}])=[\operatorname{Re}(x_{0}-ix_{1})^{m}:\operatorname{Im}(x_{0}-ix_{1})^{m}]$
,
and let
![]() $[G_{m\pm }]\in W(k)$
be the image of the class of
$[G_{m\pm }]\in W(k)$
be the image of the class of
![]() $G_{\pm m}$
in
$G_{\pm m}$
in
![]() $\text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
under the surjection
$\text{End}_{\operatorname{SH}(k)}(\mathbb{S}_{k})=\operatorname{GW}(k)$
under the surjection
![]() $\operatorname{GW}(k)\rightarrow W(k)$
. Let
$\operatorname{GW}(k)\rightarrow W(k)$
. Let
![]() $p$
be a prime. If
$p$
be a prime. If
![]() $\text{char}k=\ell >0$
we suppose that
$\text{char}k=\ell >0$
we suppose that
![]() $(\ell ,2p)=1$
. Then
$(\ell ,2p)=1$
. Then
![]() $[G_{p\pm }]=\pm p\cdot \langle 1\rangle$
.
$[G_{p\pm }]=\pm p\cdot \langle 1\rangle$
.
Proof. We first consider the case of characteristic zero; we may assume
![]() $k=\mathbb{Q}$
. We compute the
$k=\mathbb{Q}$
. We compute the
![]() $\mathbb{A}^{1}$
-degree of
$\mathbb{A}^{1}$
-degree of
![]() $g:=G_{p\pm }:\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
as the Brouwer degree (see [Reference Morel31, Chapter 2]): take
$g:=G_{p\pm }:\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
as the Brouwer degree (see [Reference Morel31, Chapter 2]): take
![]() $\mathbb{A}^{1}\subset \mathbb{P}^{1}$
the open subscheme
$\mathbb{A}^{1}\subset \mathbb{P}^{1}$
the open subscheme
![]() $x_{1}\neq 0$
and use the parameter
$x_{1}\neq 0$
and use the parameter
![]() $t=x_{0}/x_{1}$
on
$t=x_{0}/x_{1}$
on
![]() $\mathbb{A}^{1}$
. We pick a regular value
$\mathbb{A}^{1}$
. We pick a regular value
![]() $s\in \mathbb{A}^{1}(\mathbb{Q})\subset \mathbb{P}^{1}(\mathbb{Q})$
with
$s\in \mathbb{A}^{1}(\mathbb{Q})\subset \mathbb{P}^{1}(\mathbb{Q})$
with
![]() $g^{-1}(s)\subset \mathbb{A}^{1}$
, and take the sum of the trace forms
$g^{-1}(s)\subset \mathbb{A}^{1}$
, and take the sum of the trace forms
![]() $Tr_{\mathbb{Q}(t_{i})/\mathbb{Q}}$
of the 1-dimensional quadratic forms
$Tr_{\mathbb{Q}(t_{i})/\mathbb{Q}}$
of the 1-dimensional quadratic forms
![]() $\langle \frac{dg}{dt}(t_{i})\rangle \in \operatorname{GW}(k(t_{i}))$
at the closed point
$\langle \frac{dg}{dt}(t_{i})\rangle \in \operatorname{GW}(k(t_{i}))$
at the closed point
![]() $t_{i}$
of inverse image
$t_{i}$
of inverse image
![]() $g^{-1}(s)=\{t_{1},\ldots ,t_{r}\}$
.
$g^{-1}(s)=\{t_{1},\ldots ,t_{r}\}$
.
We first consider the case
![]() $g=G_{p+}$
with
$g=G_{p+}$
with
![]() $p$
odd. We take
$p$
odd. We take
![]() $s=[0:1]$
.
$s=[0:1]$
.
![]() $g^{-1}(s)$
consists of two closed points:
$g^{-1}(s)$
consists of two closed points:
![]() $t_{0}=[0:1]$
and
$t_{0}=[0:1]$
and
![]() $t_{1}\in \{x_{0}\neq 0\}\subset \mathbb{P}^{1}$
. Indeed
$t_{1}\in \{x_{0}\neq 0\}\subset \mathbb{P}^{1}$
. Indeed
![]() $g^{-1}([0:1])$
is the set of solutions to
$g^{-1}([0:1])$
is the set of solutions to
![]() $\operatorname{Im}(a+ib)^{p}=0$
, up to scaling. One solution is
$\operatorname{Im}(a+ib)^{p}=0$
, up to scaling. One solution is
![]() $[a:b]=[0:1]$
, since
$[a:b]=[0:1]$
, since
![]() $p$
is odd. For
$p$
is odd. For
![]() $a\neq 0$
, we look for solutions in
$a\neq 0$
, we look for solutions in
![]() $\mathbb{C}$
(up to scaling by
$\mathbb{C}$
(up to scaling by
![]() $\mathbb{R}$
) to
$\mathbb{R}$
) to
which gives
Dividing by
![]() $\unicode[STIX]{x1D707}^{1/4p}$
, we may assume that
$\unicode[STIX]{x1D707}^{1/4p}$
, we may assume that
![]() $(a+ib)^{4p}=1$
, in other words,
$(a+ib)^{4p}=1$
, in other words,
![]() $a+ib$
is a
$a+ib$
is a
![]() $4p$
th root of unity. The real number
$4p$
th root of unity. The real number
![]() $a/b$
is thus a number of the form
$a/b$
is thus a number of the form
![]() $\cot (m\unicode[STIX]{x1D70B}/2p)$
, and the set of
$\cot (m\unicode[STIX]{x1D70B}/2p)$
, and the set of
![]() $p-1$
solutions
$p-1$
solutions
![]() $[a:b]\in \mathbb{P}^{1}(\mathbb{C})$
with
$[a:b]\in \mathbb{P}^{1}(\mathbb{C})$
with
![]() $a\neq 0$
is exactly the set
$a\neq 0$
is exactly the set
As
is in the real subfield
![]() $F_{p}\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{4p})$
, which has degree
$F_{p}\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{4p})$
, which has degree
![]() $p-1$
over
$p-1$
over
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
![]() $S$
consists of the
$S$
consists of the
![]() $p-1$
conjugates of
$p-1$
conjugates of
![]() $\cot (\unicode[STIX]{x1D70B}/2p)$
over
$\cot (\unicode[STIX]{x1D70B}/2p)$
over
![]() $\mathbb{Q}$
, it follows that the closed point
$\mathbb{Q}$
, it follows that the closed point
![]() $t_{1}=[a:1]$
of
$t_{1}=[a:1]$
of
![]() $\mathbb{P}^{1}(\mathbb{Q})$
corresponding to
$\mathbb{P}^{1}(\mathbb{Q})$
corresponding to
![]() $[\cot (\unicode[STIX]{x1D70B}/2p):1]\in \mathbb{P}^{1}(\bar{\mathbb{Q}})$
has residue field
$[\cot (\unicode[STIX]{x1D70B}/2p):1]\in \mathbb{P}^{1}(\bar{\mathbb{Q}})$
has residue field
![]() $F_{p}$
.
$F_{p}$
.
We now compute the derivative
![]() $g^{\prime }(t)=dg/dt$
of
$g^{\prime }(t)=dg/dt$
of
![]() $g$
at
$g$
at
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{1}$
, first for
$t_{1}$
, first for
![]() $p\equiv 1\,\text{mod}\,4$
.
$p\equiv 1\,\text{mod}\,4$
.
We use the parameter
![]() $t=x_{0}/x_{1}$
, so
$t=x_{0}/x_{1}$
, so
At
![]() $t_{0}=[0:1]$
, we find
$t_{0}=[0:1]$
, we find
so
![]() $g^{\prime }(0)=p$
, which gives us the term
$g^{\prime }(0)=p$
, which gives us the term
![]() $\langle p\rangle$
.
$\langle p\rangle$
.
We now consider
![]() $t_{1}=[a_{1}:1]$
since
$t_{1}=[a_{1}:1]$
since
![]() $g(t)$
is a rational function in one variable
$g(t)$
is a rational function in one variable
![]() $t$
, to make the computation of
$t$
, to make the computation of
![]() $g^{\prime }(t)$
we may consider
$g^{\prime }(t)$
we may consider
![]() $g$
as a real-valued function of a real variable
$g$
as a real-valued function of a real variable
![]() $t$
. We change coordinates:
$t$
. We change coordinates:
![]() $x_{0}=r\cos \unicode[STIX]{x1D703}$
,
$x_{0}=r\cos \unicode[STIX]{x1D703}$
,
![]() $x_{1}=r\sin \unicode[STIX]{x1D703}$
,
$x_{1}=r\sin \unicode[STIX]{x1D703}$
,
![]() $t=\cot \unicode[STIX]{x1D703}$
, and
$t=\cot \unicode[STIX]{x1D703}$
, and
Thus
 $$\begin{eqnarray}\displaystyle \frac{dg}{dt} & = & \displaystyle \left(\frac{d\cot p\unicode[STIX]{x1D703}}{d\unicode[STIX]{x1D703}}\right)\cdot \left(\frac{dt}{d\unicode[STIX]{x1D703}}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle p\cdot \frac{-1}{\sin ^{2}p\unicode[STIX]{x1D703}}\cdot (-\sin ^{2}\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & = & \displaystyle p\cdot \frac{\sin ^{2}\unicode[STIX]{x1D703}}{\sin ^{2}p\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & = & \displaystyle \frac{p\cdot (1+t^{2})^{p-1}}{h(t)^{2}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{dg}{dt} & = & \displaystyle \left(\frac{d\cot p\unicode[STIX]{x1D703}}{d\unicode[STIX]{x1D703}}\right)\cdot \left(\frac{dt}{d\unicode[STIX]{x1D703}}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle p\cdot \frac{-1}{\sin ^{2}p\unicode[STIX]{x1D703}}\cdot (-\sin ^{2}\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & = & \displaystyle p\cdot \frac{\sin ^{2}\unicode[STIX]{x1D703}}{\sin ^{2}p\unicode[STIX]{x1D703}}\nonumber\\ \displaystyle & = & \displaystyle \frac{p\cdot (1+t^{2})^{p-1}}{h(t)^{2}}\nonumber\end{eqnarray}$$
with
 $$\begin{eqnarray}h(t)=\mathop{\sum }_{j=0}^{p-1/2}(-1)^{j}\left(\begin{array}{@{}c@{}}p\\ p-2j-1\end{array}\right)t^{p-2j-1}.\end{eqnarray}$$
$$\begin{eqnarray}h(t)=\mathop{\sum }_{j=0}^{p-1/2}(-1)^{j}\left(\begin{array}{@{}c@{}}p\\ p-2j-1\end{array}\right)t^{p-2j-1}.\end{eqnarray}$$
As
![]() $\mathbb{Q}(\sqrt{(-1)^{p-1/2}p})\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, it follows that
$\mathbb{Q}(\sqrt{(-1)^{p-1/2}p})\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
, it follows that
![]() $\mathbb{Q}(\sqrt{p})\subset F_{p}$
, so
$\mathbb{Q}(\sqrt{p})\subset F_{p}$
, so
![]() $p$
is a square in
$p$
is a square in
![]() $F_{p}$
and thus
$F_{p}$
and thus
![]() $g^{\prime }(t_{1})$
is a square in
$g^{\prime }(t_{1})$
is a square in
![]() $F_{p}$
. This gives the
$F_{p}$
. This gives the
![]() $\mathbb{A}^{1}$
Brouwer degree of
$\mathbb{A}^{1}$
Brouwer degree of
![]() $g$
as
$g$
as
which by Lemma 7.3 below is equivalent to a sum of
![]() $p$
squares, so
$p$
squares, so
![]() $[G_{p+}]=p\cdot \langle 1\rangle \in W(k)$
.
$[G_{p+}]=p\cdot \langle 1\rangle \in W(k)$
.
Next, we take
![]() $g=G_{p-}$
,
$g=G_{p-}$
,
![]() $p$
still odd. We have
$p$
still odd. We have
which is exactly the negative of the case
![]() $G_{p+}$
, so
$G_{p+}$
, so
![]() $g^{\prime }(0)=-p$
and
$g^{\prime }(0)=-p$
and
![]() $g^{\prime }(t_{1})=\frac{-p(1+a_{1})^{p-1}}{h(a_{1})^{2}}$
. This gives
$g^{\prime }(t_{1})=\frac{-p(1+a_{1})^{p-1}}{h(a_{1})^{2}}$
. This gives
For
![]() $p=2$
, we have
$p=2$
, we have
With
![]() $t=x_{0}/x_{1}$
, this gives the map
$t=x_{0}/x_{1}$
, this gives the map
so
![]() $g^{-1}(0)=\{1,-1\}$
,
$g^{-1}(0)=\{1,-1\}$
,
![]() $g^{\prime }(1)=g^{\prime }(-1)=1$
and the
$g^{\prime }(1)=g^{\prime }(-1)=1$
and the
![]() $\mathbb{A}^{1}$
Brouwer degree is
$\mathbb{A}^{1}$
Brouwer degree is
![]() $\langle 1\rangle +\langle 1\rangle =2\langle 1\rangle$
.
$\langle 1\rangle +\langle 1\rangle =2\langle 1\rangle$
.
Similarly
With
![]() $t=x_{0}/x_{1}$
, this is the map
$t=x_{0}/x_{1}$
, this is the map
and the
![]() $\mathbb{A}^{1}$
Brouwer degree is
$\mathbb{A}^{1}$
Brouwer degree is
![]() $\langle -1\rangle +\langle -1\rangle =-2\langle 1\rangle \in W(k)$
.
$\langle -1\rangle +\langle -1\rangle =-2\langle 1\rangle \in W(k)$
.
We now consider
![]() $k$
of characteristic
$k$
of characteristic
![]() $\ell >0$
with
$\ell >0$
with
![]() $(\ell ,2p)=1$
. We take
$(\ell ,2p)=1$
. We take
![]() $k=\mathbb{F}_{\ell }$
,
$k=\mathbb{F}_{\ell }$
,
![]() $\ell \neq 2,p$
and we use the same argument as above, with the following modifications, first for odd
$\ell \neq 2,p$
and we use the same argument as above, with the following modifications, first for odd
![]() $p$
:
$p$
:
(i) For
 $F\in \{\mathbb{Q}(\unicode[STIX]{x1D701}_{4p}),\mathbb{Q}(\unicode[STIX]{x1D701}_{p}),F_{p},\mathbb{Q}(i),\mathbb{Q}(\sqrt{p})\}$
, the number ring
$F\in \{\mathbb{Q}(\unicode[STIX]{x1D701}_{4p}),\mathbb{Q}(\unicode[STIX]{x1D701}_{p}),F_{p},\mathbb{Q}(i),\mathbb{Q}(\sqrt{p})\}$
, the number ring
 ${\mathcal{O}}_{F}$
is unramified at
${\mathcal{O}}_{F}$
is unramified at
 $\ell$
. In the above discussion, we replace
$\ell$
. In the above discussion, we replace
 $F$
with the étale algebra
$F$
with the étale algebra
 ${\mathcal{O}}_{F}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
.
${\mathcal{O}}_{F}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
.(ii) We note that
 $\cot (\unicode[STIX]{x1D70B}/2p)\in F_{p}$
is actually an algebraic integer; we replace
$\cot (\unicode[STIX]{x1D70B}/2p)\in F_{p}$
is actually an algebraic integer; we replace
 $\cot (\unicode[STIX]{x1D70B}/2p)\in {\mathcal{O}}_{F_{p}}$
with its image in
$\cot (\unicode[STIX]{x1D70B}/2p)\in {\mathcal{O}}_{F_{p}}$
with its image in
 ${\mathcal{O}}_{F_{p}}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
. This shows that the closures of
${\mathcal{O}}_{F_{p}}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
. This shows that the closures of
 $0,a_{1}$
in
$0,a_{1}$
in
 $\text{Spec }\mathbb{Z}[t]$
are finite over
$\text{Spec }\mathbb{Z}[t]$
are finite over
 $\text{Spec }\mathbb{Z}$
; we let
$\text{Spec }\mathbb{Z}$
; we let
 $\bar{0},\bar{a}_{1}\in \text{Spec }\mathbb{F}_{\ell }[t]$
denote their respective specializations.
$\bar{0},\bar{a}_{1}\in \text{Spec }\mathbb{F}_{\ell }[t]$
denote their respective specializations.(iii) We replace the polynomials
 $\operatorname{Re}(x_{0}+ix_{1})^{p},\operatorname{Im}(x_{0}+ix_{1})^{p}\in \mathbb{Z}[x_{0},x_{1}]$
with their respective images in
$\operatorname{Re}(x_{0}+ix_{1})^{p},\operatorname{Im}(x_{0}+ix_{1})^{p}\in \mathbb{Z}[x_{0},x_{1}]$
with their respective images in
 $\mathbb{F}_{\ell }[x_{0},x_{1}]$
. Letting
$\mathbb{F}_{\ell }[x_{0},x_{1}]$
. Letting
 $\mathfrak{m}_{0,a_{1}}\subset \mathbb{Z}_{(\ell )}[t]$
be the ideal of
$\mathfrak{m}_{0,a_{1}}\subset \mathbb{Z}_{(\ell )}[t]$
be the ideal of
 $\{0,a_{1}\}$
, we similarly replace
$\{0,a_{1}\}$
, we similarly replace
 $h(t)\in \mathbb{Z}[t]$
and
$h(t)\in \mathbb{Z}[t]$
and
 $g(t)\in \mathbb{Z}_{(\ell )}[t]_{(\mathfrak{m}_{0,a_{1}})}$
with
$g(t)\in \mathbb{Z}_{(\ell )}[t]_{(\mathfrak{m}_{0,a_{1}})}$
with
 $\bar{h}(t)\in \mathbb{F}_{\ell }[t]$
and
$\bar{h}(t)\in \mathbb{F}_{\ell }[t]$
and
 $\bar{g}(t)\in \mathbb{F}_{\ell }[t]_{(\bar{\mathfrak{m}}_{\bar{0},\bar{a}_{1}})}$
.
$\bar{g}(t)\in \mathbb{F}_{\ell }[t]_{(\bar{\mathfrak{m}}_{\bar{0},\bar{a}_{1}})}$
.(iv) We replace the trace form
 $Q_{4p}$
for
$Q_{4p}$
for
 $F_{p}$
over
$F_{p}$
over
 $\mathbb{Q}$
with the trace form
$\mathbb{Q}$
with the trace form
 $\bar{Q}_{4p}$
for the étale algebra
$\bar{Q}_{4p}$
for the étale algebra
 ${\mathcal{O}}_{F_{p}}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
over
${\mathcal{O}}_{F_{p}}\otimes _{\mathbb{Z}}\mathbb{F}_{\ell }$
over
 $\mathbb{F}_{\ell }$
. Noting again that
$\mathbb{F}_{\ell }$
. Noting again that
 ${\mathcal{O}}_{F_{p}}$
is unramified at
${\mathcal{O}}_{F_{p}}$
is unramified at
 $q$
, it follows from Lemma 7.3 and a specialization argument that
$q$
, it follows from Lemma 7.3 and a specialization argument that
 $\langle p\rangle +\bar{Q}_{4p}=\sum _{i=1}^{p}x_{i}^{2}$
in
$\langle p\rangle +\bar{Q}_{4p}=\sum _{i=1}^{p}x_{i}^{2}$
in
 $\operatorname{GW}(\mathbb{F}_{\ell })$
. With these changes and comments, the argument for characteristic zero goes through in characteristic
$\operatorname{GW}(\mathbb{F}_{\ell })$
. With these changes and comments, the argument for characteristic zero goes through in characteristic
 $\ell$
.
$\ell$
.
For
![]() $p=2$
,
$p=2$
,
![]() $\ell \neq 2$
, the direct computation given for
$\ell \neq 2$
, the direct computation given for
![]() $\mathbb{P}(\unicode[STIX]{x1D713}_{2})$
goes through over
$\mathbb{P}(\unicode[STIX]{x1D713}_{2})$
goes through over
![]() $\mathbb{F}_{\ell }$
without change.
$\mathbb{F}_{\ell }$
without change.
Lemma 7.3. Let
![]() $p$
be an odd prime,
$p$
be an odd prime,
![]() $\unicode[STIX]{x1D701}_{4p}$
a primitive
$\unicode[STIX]{x1D701}_{4p}$
a primitive
![]() $4p$
th root of unity and let
$4p$
th root of unity and let
![]() $F_{p}$
be the real subfield
$F_{p}$
be the real subfield
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{4p}+\unicode[STIX]{x1D701}_{4p}^{-1})$
of
$\mathbb{Q}(\unicode[STIX]{x1D701}_{4p}+\unicode[STIX]{x1D701}_{4p}^{-1})$
of
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{4p})$
. Let
$\mathbb{Q}(\unicode[STIX]{x1D701}_{4p})$
. Let
![]() $Q_{4p}$
denote the trace form for the field extension
$Q_{4p}$
denote the trace form for the field extension
![]() $F_{p}/\mathbb{Q}$
. Then the quadratic form
$F_{p}/\mathbb{Q}$
. Then the quadratic form
![]() $T_{p}:=\langle p\rangle +Q_{4p}$
is equivalent to the sum of squares
$T_{p}:=\langle p\rangle +Q_{4p}$
is equivalent to the sum of squares
![]() $\sum _{i=1}^{p}x_{i}^{2}$
.
$\sum _{i=1}^{p}x_{i}^{2}$
.
Proof. We have the lattice
![]() $(\mathbb{Z}^{n},\cdot )$
, with
$(\mathbb{Z}^{n},\cdot )$
, with
![]() $\cdot$
the usual dot product. For
$\cdot$
the usual dot product. For
![]() $n\geqslant 2$
an integer, we have the sublattice
$n\geqslant 2$
an integer, we have the sublattice
![]() $A_{n-1}$
of
$A_{n-1}$
of
![]() $(\mathbb{Z}^{n},\cdot )$
, given as the hyperplane
$(\mathbb{Z}^{n},\cdot )$
, given as the hyperplane
this gives us the integral quadratic form
![]() $q_{A_{n-1}}$
. Bayer and Suarez [Reference Bayer-Fluckiger and Suarez8, page 222] have shown that
$q_{A_{n-1}}$
. Bayer and Suarez [Reference Bayer-Fluckiger and Suarez8, page 222] have shown that
![]() $q_{A_{p-1}}$
is isometric to an integral model for
$q_{A_{p-1}}$
is isometric to an integral model for
![]() $Q_{4p}$
. Thus
$Q_{4p}$
. Thus
![]() $Q_{4p}+\langle p\rangle$
is isometric to the quadratic form associated to the full sublattice
$Q_{4p}+\langle p\rangle$
is isometric to the quadratic form associated to the full sublattice
![]() $A_{p-1}+\mathbb{Z}\cdot (1,\ldots ,1)$
of
$A_{p-1}+\mathbb{Z}\cdot (1,\ldots ,1)$
of
![]() $(\mathbb{Z}^{p},\cdot )$
. As
$(\mathbb{Z}^{p},\cdot )$
. As
it follows that
![]() $Q_{4p}+\langle p\rangle$
is equivalent (as a quadratic form over
$Q_{4p}+\langle p\rangle$
is equivalent (as a quadratic form over
![]() $\mathbb{Q}$
) to
$\mathbb{Q}$
) to
![]() $p\langle 1\rangle$
.
$p\langle 1\rangle$
.
Another proof uses Serre’s theorem [Reference Serre37, Théorème 1] on the Hasse–Witt invariant of trace forms; we sketch this proof. For
![]() $\unicode[STIX]{x1D701}_{n}$
a primitive
$\unicode[STIX]{x1D701}_{n}$
a primitive
![]() $n$
th root of unity, we set
$n$
th root of unity, we set
![]() $\unicode[STIX]{x1D709}_{n,j}:=\unicode[STIX]{x1D701}_{n}^{j}+\unicode[STIX]{x1D701}_{n}^{-j}$
and
$\unicode[STIX]{x1D709}_{n,j}:=\unicode[STIX]{x1D701}_{n}^{j}+\unicode[STIX]{x1D701}_{n}^{-j}$
and
![]() $\unicode[STIX]{x1D702}_{n,j}=\unicode[STIX]{x1D701}_{n}^{j}-\unicode[STIX]{x1D701}_{n}^{-j}$
and set
$\unicode[STIX]{x1D702}_{n,j}=\unicode[STIX]{x1D701}_{n}^{j}-\unicode[STIX]{x1D701}_{n}^{-j}$
and set
![]() $\unicode[STIX]{x1D709}_{n}=\unicode[STIX]{x1D709}_{n,1}$
. Let
$\unicode[STIX]{x1D709}_{n}=\unicode[STIX]{x1D709}_{n,1}$
. Let
![]() $Q_{p}$
be the trace form
$Q_{p}$
be the trace form
![]() $\text{Tr}_{\mathbb{Q}(\unicode[STIX]{x1D709}_{p})/\mathbb{Q}}$
. Using Serre’s theorem and the fact that the inclusion
$\text{Tr}_{\mathbb{Q}(\unicode[STIX]{x1D709}_{p})/\mathbb{Q}}$
. Using Serre’s theorem and the fact that the inclusion
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{p})\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
solves the embedding problem for
$\mathbb{Q}(\unicode[STIX]{x1D709}_{p})\subset \mathbb{Q}(\unicode[STIX]{x1D701}_{p})$
solves the embedding problem for
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
[Reference Serre37, Section 3.1.3], we find
$\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
[Reference Serre37, Section 3.1.3], we find
Since
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
is totally real,
$\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
is totally real,
![]() $Q_{p}$
has signature equal to its rank
$Q_{p}$
has signature equal to its rank
![]() $(p-1)/2$
; by comparing the complete set of invariants: rank signature, discriminant, Hasse–Witt invariant (see e.g. [Reference Scharlau35, Chapter 5, Theorems 3.4 and 6.4]), we have the equivalence of quadratic forms over
$(p-1)/2$
; by comparing the complete set of invariants: rank signature, discriminant, Hasse–Witt invariant (see e.g. [Reference Scharlau35, Chapter 5, Theorems 3.4 and 6.4]), we have the equivalence of quadratic forms over
![]() $\mathbb{Q}$
:
$\mathbb{Q}$
:
We now compute the discriminant and Hasse–Witt invariant for the trace form
![]() $Q_{4p}:=\text{Tr}_{\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})/\mathbb{Q}}$
. We have the
$Q_{4p}:=\text{Tr}_{\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})/\mathbb{Q}}$
. We have the
![]() $\mathbb{Q}$
-basis of
$\mathbb{Q}$
-basis of
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
,
$\mathbb{Q}(\unicode[STIX]{x1D709}_{p})$
,
We extend this to the basis
for
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})$
. Letting
$\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})$
. Letting
![]() $V_{1}$
be the
$V_{1}$
be the
![]() $\mathbb{Q}$
-subspace spanned by the
$\mathbb{Q}$
-subspace spanned by the
![]() $\unicode[STIX]{x1D709}_{p,j}$
und
$\unicode[STIX]{x1D709}_{p,j}$
und
![]() $V_{2}$
the
$V_{2}$
the
![]() $\mathbb{Q}$
-subspace spanned by the
$\mathbb{Q}$
-subspace spanned by the
![]() $i\unicode[STIX]{x1D702}_{p,j}$
, it follows from a direct computation that
$i\unicode[STIX]{x1D702}_{p,j}$
, it follows from a direct computation that
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are orthogonal with respect to
$V_{2}$
are orthogonal with respect to
![]() $Q_{4p}$
, that
$Q_{4p}$
, that
![]() $Q_{4p}$
restricted to
$Q_{4p}$
restricted to
![]() $V_{1}$
is equal to
$V_{1}$
is equal to
![]() $2\cdot Q_{p}$
and that the restriction of
$2\cdot Q_{p}$
and that the restriction of
![]() $Q_{4p}$
to
$Q_{4p}$
to
![]() $V_{2}$
is (in this basis) the diagonal form
$V_{2}$
is (in this basis) the diagonal form
![]() $(p-1)/2\cdot \langle 2p\rangle$
. In other words
$(p-1)/2\cdot \langle 2p\rangle$
. In other words
Using this, one computes the discriminant and Hasse–Witt invariant of
![]() $Q_{4p}+\langle p\rangle$
and finds the discriminant is 1 modulo squares, and the Hasse–Witt invariant is zero. Since
$Q_{4p}+\langle p\rangle$
and finds the discriminant is 1 modulo squares, and the Hasse–Witt invariant is zero. Since
![]() $\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})$
is totally real,
$\mathbb{Q}(\unicode[STIX]{x1D709}_{4p})$
is totally real,
![]() $Q_{4p}+\langle p\rangle$
has signature
$Q_{4p}+\langle p\rangle$
has signature
![]() $p$
. This shows that
$p$
. This shows that
![]() $Q_{4p}+\langle p\rangle \sim p\langle 1\rangle$
.
$Q_{4p}+\langle p\rangle \sim p\langle 1\rangle$
.
8 Characteristic classes of symmetric powers
For a positive integer
![]() $m$
we write
$m$
we write
![]() $m!!$
for the product
$m!!$
for the product
For
![]() $F=ke_{1}\oplus ke_{2}$
, we give
$F=ke_{1}\oplus ke_{2}$
, we give
![]() $\operatorname{Sym}^{m}F$
the oriented basis
$\operatorname{Sym}^{m}F$
the oriented basis
![]() $e_{1}^{m},e_{1}^{m-1}e_{2},\ldots ,e_{1}e_{2}^{m-1},e_{2}^{m}$
. Given a two-dimensional representation
$e_{1}^{m},e_{1}^{m-1}e_{2},\ldots ,e_{1}e_{2}^{m-1},e_{2}^{m}$
. Given a two-dimensional representation
![]() $\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{SL}_{2}$
, this defines the representation
$\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{SL}_{2}$
, this defines the representation
![]() $\operatorname{Sym}^{m}\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{SL}_{m+1}$
.
$\operatorname{Sym}^{m}\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{SL}_{m+1}$
.
Theorem 8.1. Let
![]() $m$
be a positive integer,
$m$
be a positive integer,
![]() $k$
a perfect field. Let
$k$
a perfect field. Let
![]() $E\rightarrow X$
be a rank two vector bundle on some
$E\rightarrow X$
be a rank two vector bundle on some
![]() $X\in \mathbf{Sm}/k$
and consider the Euler class
$X\in \mathbf{Sm}/k$
and consider the Euler class
![]() $e(\operatorname{Sym}^{m}E)\in H^{m+1}(X,{\mathcal{W}}(\operatorname{det}^{-1}\operatorname{Sym}^{m}E))$
. Then for
$e(\operatorname{Sym}^{m}E)\in H^{m+1}(X,{\mathcal{W}}(\operatorname{det}^{-1}\operatorname{Sym}^{m}E))$
. Then for
![]() $m=2r+1$
odd, and
$m=2r+1$
odd, and
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
, or of positive characteristic
$0$
, or of positive characteristic
![]() $\ell$
prime to
$\ell$
prime to
![]() $2m$
, we have
$2m$
, we have
For
![]() $k$
an arbitrary field of characteristic
$k$
an arbitrary field of characteristic
![]() $\neq 2$
and for
$\neq 2$
and for
![]() $m$
even, we have
$m$
even, we have
![]() $e(\operatorname{Sym}^{m}E)=0$
.
$e(\operatorname{Sym}^{m}E)=0$
.
The total Pontryagin class
![]() $p:=1+\sum _{i\geqslant 1}p_{i}$
is given by
$p:=1+\sum _{i\geqslant 1}p_{i}$
is given by
Proof. We first compute the Euler class. The bundle
![]() $\operatorname{Sym}^{m}E$
has rank
$\operatorname{Sym}^{m}E$
has rank
![]() $m+1$
, so has odd rank if
$m+1$
, so has odd rank if
![]() $m$
is even, and therefore has vanishing Euler class in Witt cohomology by [Reference Levine25, Proposition 7.3] or Lemma 4.3. We consider the case of odd
$m$
is even, and therefore has vanishing Euler class in Witt cohomology by [Reference Levine25, Proposition 7.3] or Lemma 4.3. We consider the case of odd
![]() $m=2r+1$
.
$m=2r+1$
.
It clearly suffices to prove the formula for the universal bundle
![]() $E_{2}\rightarrow \operatorname{BGL}_{2}$
. By Theorem 4.1, it suffices to prove the formula for the universal bundle
$E_{2}\rightarrow \operatorname{BGL}_{2}$
. By Theorem 4.1, it suffices to prove the formula for the universal bundle
![]() $E_{2}\rightarrow \operatorname{BSL}_{2}$
and then by Proposition 5.3, we reduce to the case of the rank two bundle
$E_{2}\rightarrow \operatorname{BSL}_{2}$
and then by Proposition 5.3, we reduce to the case of the rank two bundle
![]() $\tilde{E}_{2}=\tilde{O} (1)\rightarrow BN$
.
$\tilde{E}_{2}=\tilde{O} (1)\rightarrow BN$
.
It is easy to see that we have an orientation-preserving isomorphism
where we write
![]() $\unicode[STIX]{x1D70C}_{n}^{+1}$
for
$\unicode[STIX]{x1D70C}_{n}^{+1}$
for
![]() $\unicode[STIX]{x1D70C}_{n}$
and
$\unicode[STIX]{x1D70C}_{n}$
and
![]() $\unicode[STIX]{x1D70C}_{n}^{-1}$
for
$\unicode[STIX]{x1D70C}_{n}^{-1}$
for
![]() $\unicode[STIX]{x1D70C}_{n}^{-}$
. This gives the isomorphism
$\unicode[STIX]{x1D70C}_{n}^{-}$
. This gives the isomorphism
and thus by Theorem 7.1 we have
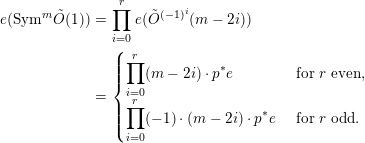 $$\begin{eqnarray}\displaystyle e(\operatorname{Sym}^{m}\tilde{O} (1)) & = & \displaystyle \mathop{\prod }_{i=0}^{r}e(\tilde{O} ^{(-1)^{i}}(m-2i))\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\prod }_{i=0}^{r}(m-2i)\cdot p^{\ast }e\quad & \text{ for }r\text{ even,}\\ \displaystyle \mathop{\prod }_{i=0}^{r}(-1)\cdot (m-2i)\cdot p^{\ast }e\quad & \text{ for }r\text{ odd.}\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e(\operatorname{Sym}^{m}\tilde{O} (1)) & = & \displaystyle \mathop{\prod }_{i=0}^{r}e(\tilde{O} ^{(-1)^{i}}(m-2i))\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\prod }_{i=0}^{r}(m-2i)\cdot p^{\ast }e\quad & \text{ for }r\text{ even,}\\ \displaystyle \mathop{\prod }_{i=0}^{r}(-1)\cdot (m-2i)\cdot p^{\ast }e\quad & \text{ for }r\text{ odd.}\end{array}\right.\nonumber\end{eqnarray}$$
which in either case gives
For the total Pontryagin class, we recall that
![]() $p_{i}$
lives in
$p_{i}$
lives in
![]() $H^{4i}(-,{\mathcal{W}})$
, and for a rank 2 bundle
$H^{4i}(-,{\mathcal{W}})$
, and for a rank 2 bundle
![]() $F$
,
$F$
,
![]() $p_{1}(F)=e(F)^{2}$
and the higher Pontryagin classes vanish. For a rank 1 bundle
$p_{1}(F)=e(F)^{2}$
and the higher Pontryagin classes vanish. For a rank 1 bundle
![]() $F$
,
$F$
,
![]() $p(F)=1$
, and for arbitrary bundles
$p(F)=1$
, and for arbitrary bundles
![]() $F,F^{\prime }$
,
$F,F^{\prime }$
,
![]() $p$
satisfies the Whitney formula
$p$
satisfies the Whitney formula
Thus, for
![]() $m=2r$
even, we have
$m=2r$
even, we have
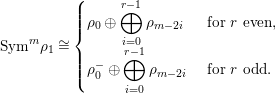 $$\begin{eqnarray}\operatorname{Sym}^{m}\unicode[STIX]{x1D70C}_{1}\cong \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70C}_{0}\oplus \displaystyle \bigoplus _{i=0}^{r-1}\unicode[STIX]{x1D70C}_{m-2i}\quad & \text{ for }r\text{ even},\\ \unicode[STIX]{x1D70C}_{0}^{-}\oplus \displaystyle \bigoplus _{i=0}^{r-1}\unicode[STIX]{x1D70C}_{m-2i}\quad & \text{ for }r\text{ odd.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sym}^{m}\unicode[STIX]{x1D70C}_{1}\cong \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70C}_{0}\oplus \displaystyle \bigoplus _{i=0}^{r-1}\unicode[STIX]{x1D70C}_{m-2i}\quad & \text{ for }r\text{ even},\\ \unicode[STIX]{x1D70C}_{0}^{-}\oplus \displaystyle \bigoplus _{i=0}^{r-1}\unicode[STIX]{x1D70C}_{m-2i}\quad & \text{ for }r\text{ odd.}\end{array}\right.\end{eqnarray}$$
which by Theorem 7.1 gives
For
![]() $m=2r+1$
odd, we have as above
$m=2r+1$
odd, we have as above
which by Theorem 7.1 again gives
Example 8.2. Consider a smooth hypersurface
![]() $X$
in
$X$
in
![]() $\mathbb{P}_{k}^{d+1}$
of degree
$\mathbb{P}_{k}^{d+1}$
of degree
![]() $2d-1$
with
$2d-1$
with
![]() $k$
a perfect field of characteristic prime to
$k$
a perfect field of characteristic prime to
![]() $2(2d-1)$
. Counting constants, one expects
$2(2d-1)$
. Counting constants, one expects
![]() $X$
to contain finitely many lines. In fact, if
$X$
to contain finitely many lines. In fact, if
![]() $X$
is defined by a degree
$X$
is defined by a degree
![]() $2d-1$
homogeneous polynomial
$2d-1$
homogeneous polynomial
![]() $f\in k[T_{0},\ldots ,T_{d+1}]$
, then
$f\in k[T_{0},\ldots ,T_{d+1}]$
, then
![]() $f$
defines a global section
$f$
defines a global section
![]() $s_{f}$
of
$s_{f}$
of
![]() $\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, where
$\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, where
![]() $E_{2}^{\vee }$
is the dual of the tautological rank 2 subbundle
$E_{2}^{\vee }$
is the dual of the tautological rank 2 subbundle
![]() $E_{2}\subset {\mathcal{O}}_{\operatorname{Gr}}^{d+2}$
on the Grassmannian
$E_{2}\subset {\mathcal{O}}_{\operatorname{Gr}}^{d+2}$
on the Grassmannian
![]() $\operatorname{Gr}=\operatorname{Gr}(2,d+2)$
, and a line
$\operatorname{Gr}=\operatorname{Gr}(2,d+2)$
, and a line
![]() $\ell \subset \mathbb{P}^{d+1}$
is contained in
$\ell \subset \mathbb{P}^{d+1}$
is contained in
![]() $X$
exactly when
$X$
exactly when
![]() $s_{f}([\ell ])=0$
, where
$s_{f}([\ell ])=0$
, where
![]() $[\ell ]\in \operatorname{Gr}$
is the point corresponding to the 2-plane
$[\ell ]\in \operatorname{Gr}$
is the point corresponding to the 2-plane
![]() $\unicode[STIX]{x1D70B}\subset \mathbb{A}^{d+2}$
with
$\unicode[STIX]{x1D70B}\subset \mathbb{A}^{d+2}$
with
![]() $\ell =\mathbb{P}(\unicode[STIX]{x1D70B})$
. Since
$\ell =\mathbb{P}(\unicode[STIX]{x1D70B})$
. Since
![]() $\operatorname{Gr}$
has dimension
$\operatorname{Gr}$
has dimension
![]() $2d=\operatorname{rnk}\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, one would expect that for a general
$2d=\operatorname{rnk}\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, one would expect that for a general
![]() $f$
,
$f$
,
![]() $s_{f}$
would have finitely many zeros.
$s_{f}$
would have finitely many zeros.
In the case of our section
![]() $s_{f}$
, with
$s_{f}$
, with
![]() $X$
having finitely many lines, we may apply our Theorem 8.1 to find
$X$
having finitely many lines, we may apply our Theorem 8.1 to find
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x,~s_{f}(x)=0}e_{x}(\operatorname{Sym}^{2d-1}E_{2}^{\vee };s_{f}) & = & \displaystyle e(\operatorname{Sym}^{2d-1}E_{2}^{\vee })\nonumber\\ \displaystyle & = & \displaystyle (2d-1)!!e(E_{2}^{\vee })^{d}\in H^{2d} (\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x,~s_{f}(x)=0}e_{x}(\operatorname{Sym}^{2d-1}E_{2}^{\vee };s_{f}) & = & \displaystyle e(\operatorname{Sym}^{2d-1}E_{2}^{\vee })\nonumber\\ \displaystyle & = & \displaystyle (2d-1)!!e(E_{2}^{\vee })^{d}\in H^{2d} (\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d)).\nonumber\end{eqnarray}$$
Here
![]() $e_{x}(\operatorname{Sym}^{2d-1}E_{2}^{\vee };s_{f})$
is the image of the local index
$e_{x}(\operatorname{Sym}^{2d-1}E_{2}^{\vee };s_{f})$
is the image of the local index
![]() $s_{f}^{\ast }(\operatorname{th}(\operatorname{Sym}^{2d-1}E_{2}^{\vee }))\in H_{x}^{2d} (\!\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d))$
in
$s_{f}^{\ast }(\operatorname{th}(\operatorname{Sym}^{2d-1}E_{2}^{\vee }))\in H_{x}^{2d} (\!\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d))$
in
![]() $H^{2d} (\!\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d))$
. Note that
$H^{2d} (\!\operatorname{Gr},{\mathcal{W}}({\mathcal{O}}_{\operatorname{Gr}}(-d))$
. Note that
![]() $\operatorname{det}E_{2}^{\vee }={\mathcal{O}}_{\operatorname{Gr}}(1)$
(with respect to the Plücker embedding).
$\operatorname{det}E_{2}^{\vee }={\mathcal{O}}_{\operatorname{Gr}}(1)$
(with respect to the Plücker embedding).
The canonical exact sequence presenting the tangent bundle
and the canonical isomorphism
![]() $\operatorname{det}E_{2}\otimes E_{2}^{\vee }\cong {\mathcal{O}}_{\operatorname{Gr}}$
gives the isomorphism
$\operatorname{det}E_{2}\otimes E_{2}^{\vee }\cong {\mathcal{O}}_{\operatorname{Gr}}$
gives the isomorphism
![]() $\unicode[STIX]{x1D714}_{\operatorname{Gr}/k}={\mathcal{O}}_{\operatorname{Gr}}(-d-2)$
, which in turn gives the isomorphism
$\unicode[STIX]{x1D714}_{\operatorname{Gr}/k}={\mathcal{O}}_{\operatorname{Gr}}(-d-2)$
, which in turn gives the isomorphism
The pushforward
thus gives us well-defined pushforward maps
In addition, we claim that
Indeed, a linear form
![]() $L$
on
$L$
on
![]() $\mathbb{P}^{d+1}$
gives a section
$\mathbb{P}^{d+1}$
gives a section
![]() $s_{L}$
of
$s_{L}$
of
![]() $E_{2}^{\vee }$
, transverse to the 0-section, with zero-locus
$E_{2}^{\vee }$
, transverse to the 0-section, with zero-locus
![]() $z_{L}$
exactly the Grassmannian of lines contained in the hyperplane
$z_{L}$
exactly the Grassmannian of lines contained in the hyperplane
![]() $L=0$
. Taking
$L=0$
. Taking
![]() $L$
to be the coordinate
$L$
to be the coordinate
![]() $T_{i}$
,
$T_{i}$
,
![]() $i=0,\ldots ,d-1$
, the corresponding (transverse) intersection of 0-loci is the point of
$i=0,\ldots ,d-1$
, the corresponding (transverse) intersection of 0-loci is the point of
![]() $\operatorname{Gr}$
corresponding to the line
$\operatorname{Gr}$
corresponding to the line
![]() $\ell _{0}$
defined by
$\ell _{0}$
defined by
![]() $T_{0}=\cdots =T_{d-1}=0$
.
$T_{0}=\cdots =T_{d-1}=0$
.
![]() $\ell _{0}$
is a point of the big affine cell
$\ell _{0}$
is a point of the big affine cell
![]() $\operatorname{Gr}^{0}\subset \operatorname{Gr}$
consisting of the lines
$\operatorname{Gr}^{0}\subset \operatorname{Gr}$
consisting of the lines
![]() $\ell$
that do not intersect the linear subspace
$\ell$
that do not intersect the linear subspace
![]() $T_{d}=T_{d+1}=0$
. For
$T_{d}=T_{d+1}=0$
. For
![]() $\ell \in \operatorname{Gr}^{0}$
,
$\ell \in \operatorname{Gr}^{0}$
,
![]() $\ell$
intersects the hyperplane
$\ell$
intersects the hyperplane
![]() $T_{d+1}=0$
in a single point
$T_{d+1}=0$
in a single point
![]() $(x_{0},\ldots ,x_{d-1},1,0)$
and the hyperplane
$(x_{0},\ldots ,x_{d-1},1,0)$
and the hyperplane
![]() $T_{d}=0$
in a single point
$T_{d}=0$
in a single point
![]() $(y_{0},\ldots ,y_{d-1},0,1)$
, giving the coordinates
$(y_{0},\ldots ,y_{d-1},0,1)$
, giving the coordinates
![]() $(x_{0},y_{0},x_{1},y_{1},\ldots ,x_{d-1},y_{d-1})$
for
$(x_{0},y_{0},x_{1},y_{1},\ldots ,x_{d-1},y_{d-1})$
for
![]() $\operatorname{Gr}^{0}\cong \mathbb{A}^{2d}$
. The sections
$\operatorname{Gr}^{0}\cong \mathbb{A}^{2d}$
. The sections
![]() $s_{T_{d}}$
,
$s_{T_{d}}$
,
![]() $s_{T_{d+1}}$
of
$s_{T_{d+1}}$
of
![]() $E_{2}^{\vee }$
give a framing trivializing
$E_{2}^{\vee }$
give a framing trivializing
![]() $E_{2}^{\vee }$
over
$E_{2}^{\vee }$
over
![]() $\operatorname{Gr}^{0}$
and composing the map
$\operatorname{Gr}^{0}$
and composing the map
![]() $\unicode[STIX]{x1D70B}$
(8.1) with the inclusion of subbundle
$\unicode[STIX]{x1D70B}$
(8.1) with the inclusion of subbundle
![]() $\oplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
of
$\oplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
of
![]() $\oplus _{i=0}^{d+1}E_{2}^{\vee }\cdot e_{i}$
defines an isomorphism
$\oplus _{i=0}^{d+1}E_{2}^{\vee }\cdot e_{i}$
defines an isomorphism
![]() $\unicode[STIX]{x1D6FC}:\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}\rightarrow T_{\operatorname{Gr}/k}$
over
$\unicode[STIX]{x1D6FC}:\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}\rightarrow T_{\operatorname{Gr}/k}$
over
![]() $\operatorname{Gr}^{0}$
.
$\operatorname{Gr}^{0}$
.
The class
![]() $e(E_{2}^{\vee })^{d}$
is represented in
$e(E_{2}^{\vee })^{d}$
is represented in
![]() $H_{\ell _{0}}^{d} (\!\operatorname{Gr},{\mathcal{K}}^{MW}({\mathcal{O}}(-d))$
by the pullback of
$H_{\ell _{0}}^{d} (\!\operatorname{Gr},{\mathcal{K}}^{MW}({\mathcal{O}}(-d))$
by the pullback of
![]() $\operatorname{th}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})$
by the section
$\operatorname{th}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})$
by the section
![]() $s:=\sum _{i=0}^{d-1}s_{T_{i}}e_{i}$
. We can identify
$s:=\sum _{i=0}^{d-1}s_{T_{i}}e_{i}$
. We can identify
![]() $H_{\ell _{0}}^{d}(\operatorname{Gr},{\mathcal{K}}^{MW}(\operatorname{det}^{-d}E_{2}^{\vee }))$
with
$H_{\ell _{0}}^{d}(\operatorname{Gr},{\mathcal{K}}^{MW}(\operatorname{det}^{-d}E_{2}^{\vee }))$
with
![]() $\operatorname{GW}(k(\ell _{0});\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1}\otimes k(\ell _{0}))$
via the Rost–Schmid resolution. Since
$\operatorname{GW}(k(\ell _{0});\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1}\otimes k(\ell _{0}))$
via the Rost–Schmid resolution. Since
![]() $s$
is transverse to the zero-section, the element of
$s$
is transverse to the zero-section, the element of
![]() $\operatorname{GW}(k(\ell _{0});\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1})$
corresponding to
$\operatorname{GW}(k(\ell _{0});\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1})$
corresponding to
![]() $s^{\ast }(\operatorname{th}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}))$
is given by the rank one form
$s^{\ast }(\operatorname{th}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}))$
is given by the rank one form
![]() $\langle \operatorname{det}^{-1}\bar{ds}\rangle$
, where
$\langle \operatorname{det}^{-1}\bar{ds}\rangle$
, where
![]() $\bar{ds}:T_{\operatorname{Gr},\ell _{0}}\rightarrow \bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
is the composition of the differential
$\bar{ds}:T_{\operatorname{Gr},\ell _{0}}\rightarrow \bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
is the composition of the differential
![]() $ds:T_{\operatorname{Gr},\ell _{0}}\rightarrow T_{\ell _{0},0}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})$
with the projection
$ds:T_{\operatorname{Gr},\ell _{0}}\rightarrow T_{\ell _{0},0}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})$
with the projection
![]() $T_{\ell _{0},0}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})\rightarrow \bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
with kernel the tangent space to the 0-section. A direct computation shows that
$T_{\ell _{0},0}(\bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i})\rightarrow \bigoplus _{i=0}^{d-1}E_{2}^{\vee }\cdot e_{i}$
with kernel the tangent space to the 0-section. A direct computation shows that
![]() $\bar{ds}$
is exactly the inverse to
$\bar{ds}$
is exactly the inverse to
![]() $\unicode[STIX]{x1D6FC}\otimes k(\ell _{0})$
, so after using (8.1) and our trivialization of
$\unicode[STIX]{x1D6FC}\otimes k(\ell _{0})$
, so after using (8.1) and our trivialization of
![]() $E_{2}^{\vee }$
to identify
$E_{2}^{\vee }$
to identify
![]() $\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1}\otimes k(\ell _{0})$
with
$\operatorname{det}^{-d}E_{2}^{\vee }\otimes \unicode[STIX]{x1D714}_{\operatorname{Gr}/k}^{-1}\otimes k(\ell _{0})$
with
![]() $k(\ell _{0})$
we obtain the form
$k(\ell _{0})$
we obtain the form
![]() $\langle 1\rangle \in \operatorname{GW}(k(\ell _{0}))$
; as
$\langle 1\rangle \in \operatorname{GW}(k(\ell _{0}))$
; as
![]() $k=k(\ell _{0})$
, this pushes forward to
$k=k(\ell _{0})$
, this pushes forward to
![]() $\langle 1\rangle \in \operatorname{GW}(k)$
, as claimed.
$\langle 1\rangle \in \operatorname{GW}(k)$
, as claimed.
The computation above yields the class of
![]() $\unicode[STIX]{x1D70B}_{\operatorname{Gr}\ast }(\!e(\operatorname{Sym}^{2d-1}(E_{2}^{\vee }))\in W(k)$
as
$\unicode[STIX]{x1D70B}_{\operatorname{Gr}\ast }(\!e(\operatorname{Sym}^{2d-1}(E_{2}^{\vee }))\in W(k)$
as
We can lift this to an identity in
![]() $\operatorname{GW}(k)$
by computing the rank, which is just the degree of the top Chern class of
$\operatorname{GW}(k)$
by computing the rank, which is just the degree of the top Chern class of
![]() $\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, that is, the number of lines on
$\operatorname{Sym}^{2d-1}E_{2}^{\vee }$
, that is, the number of lines on
![]() $X$
over an algebraically closed field, say
$X$
over an algebraically closed field, say
![]() $N_{d}$
. This gives
$N_{d}$
. This gives
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\operatorname{Gr}\ast }\!(e(\operatorname{Sym}^{2d-1}(E_{2}^{\vee })) & = & \displaystyle (2d-1)!!\langle 1\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\frac{N_{d}-(2d-1)!!}{2}\cdot (\langle 1\rangle +\langle -1\rangle )\in \operatorname{GW}(k).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\operatorname{Gr}\ast }\!(e(\operatorname{Sym}^{2d-1}(E_{2}^{\vee })) & = & \displaystyle (2d-1)!!\langle 1\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\frac{N_{d}-(2d-1)!!}{2}\cdot (\langle 1\rangle +\langle -1\rangle )\in \operatorname{GW}(k).\nonumber\end{eqnarray}$$
For
![]() $k=\mathbb{R}$
, this recovers a computation of Okonek–Teleman [Reference Okonek and Teleman33] by taking the signature.
$k=\mathbb{R}$
, this recovers a computation of Okonek–Teleman [Reference Okonek and Teleman33] by taking the signature.
For
![]() $d=2$
,
$d=2$
,
![]() $N_{d}=27$
and we have
$N_{d}=27$
and we have
recovering a computation of Kass–Wickelgren [Reference Kass and Wickelgren23].
Additionally, Kass–Wickelgren [Reference Kass and Wickelgren22] have shown how to compute explicitly the local contribution
![]() $e_{x}(V;s)$
to the global Euler class
$e_{x}(V;s)$
to the global Euler class
![]() $e(V)$
of an isolated zero of a section
$e(V)$
of an isolated zero of a section
![]() $s$
of a vector bundle
$s$
of a vector bundle
![]() $V\rightarrow Y$
of rank equal to the dimension
$V\rightarrow Y$
of rank equal to the dimension
![]() $d$
of
$d$
of
![]() $Y$
. In case
$Y$
. In case
![]() $s$
has only isolated zeros, this gives the formula
$s$
has only isolated zeros, this gives the formula
They give a geometric interpretation of this local contribution in the case of the section
![]() $s_{f}$
for
$s_{f}$
for
![]() $d=2$
, and use their computation of the pushforward of the Euler class to deduce a mod 2 congruence for the number of lines of different geometric type defined over even and odd extensions of the base field
$d=2$
, and use their computation of the pushforward of the Euler class to deduce a mod 2 congruence for the number of lines of different geometric type defined over even and odd extensions of the base field
![]() $k$
for
$k$
for
![]() $k$
a finite field. It would be interesting to extend this geometric interpretation to the higher dimensional case.
$k$
a finite field. It would be interesting to extend this geometric interpretation to the higher dimensional case.
9 Tensor products and tensor powers
In this section we assume
![]() $\text{char}k\neq 2$
. To discuss characteristic classes of tensor products, we need to fix a canonical isomorphism
$\text{char}k\neq 2$
. To discuss characteristic classes of tensor products, we need to fix a canonical isomorphism
![]() $(\operatorname{det}E)^{\operatorname{rnk}F}\otimes (\operatorname{det}F)^{\operatorname{rnk}E}\cong \operatorname{det}(E\otimes F)$
. It suffices to do this for free
$(\operatorname{det}E)^{\operatorname{rnk}F}\otimes (\operatorname{det}F)^{\operatorname{rnk}E}\cong \operatorname{det}(E\otimes F)$
. It suffices to do this for free
![]() $R$
-modules
$R$
-modules
![]() $E=\bigoplus _{i=1}^{n}Re_{i}$
,
$E=\bigoplus _{i=1}^{n}Re_{i}$
,
![]() $F=\bigoplus _{j=1}^{m}Rf_{j}$
, functorially in
$F=\bigoplus _{j=1}^{m}Rf_{j}$
, functorially in
![]() $R$
, which we do by sending
$R$
, which we do by sending
to
Similarly, we have the canonical isomorphism
![]() $\operatorname{det}E\otimes \operatorname{det}F\cong \operatorname{det}(E\bigoplus F)$
, determined by sending
$\operatorname{det}E\otimes \operatorname{det}F\cong \operatorname{det}(E\bigoplus F)$
, determined by sending
![]() $(e_{1}\wedge \cdots \wedge e_{n})\otimes (f_{1}\wedge \cdots f_{m})$
to
$(e_{1}\wedge \cdots \wedge e_{n})\otimes (f_{1}\wedge \cdots f_{m})$
to
![]() $((e_{1},0)\wedge \cdots \wedge (e_{n},0))\wedge ((0,f_{1})\wedge \cdots (0,f_{m}))$
in the case
$((e_{1},0)\wedge \cdots \wedge (e_{n},0))\wedge ((0,f_{1})\wedge \cdots (0,f_{m}))$
in the case
![]() $E=\bigoplus _{i=1}^{n}Re_{i}$
,
$E=\bigoplus _{i=1}^{n}Re_{i}$
,
![]() $F=\bigoplus _{j=1}^{m}Rf_{j}$
.
$F=\bigoplus _{j=1}^{m}Rf_{j}$
.
Proposition 9.1. Let
![]() $E\rightarrow X$
,
$E\rightarrow X$
,
![]() $E^{\prime }\rightarrow Y$
be rank two bundles on
$E^{\prime }\rightarrow Y$
be rank two bundles on
![]() $X,Y\in \mathbf{Sm}/k$
with trivialized determinants. Then
$X,Y\in \mathbf{Sm}/k$
with trivialized determinants. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle e(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}-\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2}\in H^{4}(X\times Y,{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle p_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=2(\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}+\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2})\in H^{4}(X\times Y,{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle p_{2}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=(\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}-\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2})^{2}\in H^{8}(X\times Y,{\mathcal{W}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}-\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2}\in H^{4}(X\times Y,{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle p_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=2(\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}+\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2})\in H^{4}(X\times Y,{\mathcal{W}})\nonumber\\ \displaystyle & & \displaystyle p_{2}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=(\unicode[STIX]{x1D70B}_{1}^{\ast }e(E)^{2}-\unicode[STIX]{x1D70B}_{2}^{\ast }e(E^{\prime })^{2})^{2}\in H^{8}(X\times Y,{\mathcal{W}})\nonumber\end{eqnarray}$$
and
![]() $p_{m}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=0$
for
$p_{m}(\unicode[STIX]{x1D70B}_{1}^{\ast }E\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E^{\prime })=0$
for
![]() $m>2$
.
$m>2$
.
Proof. The last formula follows from the fact that
![]() $p_{m}(F)=0$
for
$p_{m}(F)=0$
for
![]() $2m>\operatorname{rnk}(F)$
. The formula for
$2m>\operatorname{rnk}(F)$
. The formula for
![]() $p_{2}$
follows from the formula for
$p_{2}$
follows from the formula for
![]() $e$
and the fact that
$e$
and the fact that
![]() $p_{m}(F)=e(F)^{2}$
for
$p_{m}(F)=e(F)^{2}$
for
![]() $F$
of rank
$F$
of rank
![]() $2m$
.
$2m$
.
It suffices to consider the universal case of
![]() $\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\oplus \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}$
on
$\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\oplus \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}$
on
![]() $\operatorname{BSL}_{2}\times \operatorname{BSL}_{2}$
. Let
$\operatorname{BSL}_{2}\times \operatorname{BSL}_{2}$
. Let
be the inclusions
![]() $i_{1}(x)=(x\times x_{0})$
,
$i_{1}(x)=(x\times x_{0})$
,
![]() $i_{2}(x)=x_{0}\times x$
, where
$i_{2}(x)=x_{0}\times x$
, where
![]() $x_{0}$
is the base point, and let
$x_{0}$
is the base point, and let
![]() $\unicode[STIX]{x1D6FF}:\operatorname{BSL}_{2}\rightarrow \operatorname{BSL}_{2}\times \operatorname{BSL}_{2}$
be the diagonal inclusion. We have
$\unicode[STIX]{x1D6FF}:\operatorname{BSL}_{2}\rightarrow \operatorname{BSL}_{2}\times \operatorname{BSL}_{2}$
be the diagonal inclusion. We have
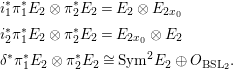 $$\begin{eqnarray}\displaystyle & & \displaystyle i_{1}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}=E_{2}\otimes E_{2x_{0}}\nonumber\\ \displaystyle & & \displaystyle i_{2}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}=E_{2x_{0}}\otimes E_{2}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}\cong \operatorname{Sym}^{2}E_{2}\oplus O_{\operatorname{BSL}_{2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i_{1}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}=E_{2}\otimes E_{2x_{0}}\nonumber\\ \displaystyle & & \displaystyle i_{2}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}=E_{2x_{0}}\otimes E_{2}\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}^{\ast }\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}\cong \operatorname{Sym}^{2}E_{2}\oplus O_{\operatorname{BSL}_{2}}.\nonumber\end{eqnarray}$$
We have a canonical isomorphism
![]() $E_{2x_{0}}\cong k^{2}$
, which gives us isomorphisms
$E_{2x_{0}}\cong k^{2}$
, which gives us isomorphisms
Furthermore, the canonical isomorphism
induces the isomorphisms
using our convention for the determinant of a tensor product and a direct sum, as described above. This gives us the identities
in terms of free modules
![]() $E=Re_{1}\oplus Re_{2}$
,
$E=Re_{1}\oplus Re_{2}$
,
![]() $F=Rf_{1}\oplus Rf_{2}$
, this arises from the fact that
$F=Rf_{1}\oplus Rf_{2}$
, this arises from the fact that
is an oriented basis for
![]() $E\otimes F$
, giving the oriented basis
$E\otimes F$
, giving the oriented basis
for
![]() $E\otimes f_{1}\oplus E\otimes f_{2}$
, while an oriented basis for
$E\otimes f_{1}\oplus E\otimes f_{2}$
, while an oriented basis for
![]() $e_{1}\otimes F\oplus e_{2}\otimes F$
is
$e_{1}\otimes F\oplus e_{2}\otimes F$
is
which introduces the sign
![]() $-1$
in the identity
$-1$
in the identity
![]() $i_{2}^{\ast }\unicode[STIX]{x1D6FC}=-\unicode[STIX]{x1D6FD}$
.
$i_{2}^{\ast }\unicode[STIX]{x1D6FC}=-\unicode[STIX]{x1D6FD}$
.
Keeping track of the orientations gives the identities
 $$\begin{eqnarray}\displaystyle i_{1}^{\ast }e(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle e(E_{2}\oplus E_{2})=e(E_{2})^{2}\nonumber\\ \displaystyle i_{2}^{\ast }e(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle -e(E_{2}\oplus E_{2})=-e(E_{2})^{2}\nonumber\\ \displaystyle \unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle e(\operatorname{Sym}^{2}E_{2})\cup e(O_{\operatorname{BSL}_{2}})=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{1}^{\ast }e(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle e(E_{2}\oplus E_{2})=e(E_{2})^{2}\nonumber\\ \displaystyle i_{2}^{\ast }e(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle -e(E_{2}\oplus E_{2})=-e(E_{2})^{2}\nonumber\\ \displaystyle \unicode[STIX]{x1D6FF}^{\ast }(\unicode[STIX]{x1D70B}_{1}^{\ast }E_{2}\otimes \unicode[STIX]{x1D70B}_{2}^{\ast }E_{2}) & = & \displaystyle e(\operatorname{Sym}^{2}E_{2})\cup e(O_{\operatorname{BSL}_{2}})=0.\nonumber\end{eqnarray}$$
On the other hand, we have
so there are uniquely defined elements
![]() $a,b,c\in W(k)$
with
$a,b,c\in W(k)$
with
The computations above together with the identities
imply that
![]() $a=1$
,
$a=1$
,
![]() $c=-1$
and
$c=-1$
and
![]() $b=0$
.
$b=0$
.
For the Pontryagin class, we recall that the Pontryagin classes are stable and are insensitive to the orientation. This gives
and using Theorem 8.1 to compute
![]() $p_{1}(\operatorname{Sym}^{2}E_{2})$
gives
$p_{1}(\operatorname{Sym}^{2}E_{2})$
gives
Computing as above gives
Remark 9.2. Combining Ananyevskiy’s
![]() $\operatorname{SL}_{2}$
splitting principle with Theorem 4.1 reduces the computation of the Euler class and Pontryagin classes in Witt cohomology of any Schur functor applied to a vector bundle to the case of a direct sum of rank 2 bundles with trivialized determinant. Via the representation theory of
$\operatorname{SL}_{2}$
splitting principle with Theorem 4.1 reduces the computation of the Euler class and Pontryagin classes in Witt cohomology of any Schur functor applied to a vector bundle to the case of a direct sum of rank 2 bundles with trivialized determinant. Via the representation theory of
![]() $\operatorname{SL}_{2}$
, this reduces the computation to the case of tensor products of symmetric powers. Using the
$\operatorname{SL}_{2}$
, this reduces the computation to the case of tensor products of symmetric powers. Using the
![]() $\operatorname{SL}_{2}$
splitting principle again, we need only know the characteristic classes of symmetric powers and the tensor product of two rank two bundles (with trivialized determinant); as this information is given by Theorem 8.1 and Proposition 9.1, we have a complete calculus for the computation of the characteristic classes, at least over a field of characteristic zero.
$\operatorname{SL}_{2}$
splitting principle again, we need only know the characteristic classes of symmetric powers and the tensor product of two rank two bundles (with trivialized determinant); as this information is given by Theorem 8.1 and Proposition 9.1, we have a complete calculus for the computation of the characteristic classes, at least over a field of characteristic zero.
In positive characteristic, our calculus is limited by the restriction on the characteristic in Theorem 8.1, but one still has a partial calculus for the characteristic classes of Schur functors of degree
![]() ${\leqslant}m$
in characteristics
${\leqslant}m$
in characteristics
![]() $\ell >m$
.
$\ell >m$
.