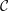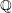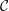1 Introduction
A log surface
![]() $(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
![]() ${\mathcal{C}}$
consists of a compact normal analytic surface
${\mathcal{C}}$
consists of a compact normal analytic surface
![]() $X$
that is bimeromorphically equivalent to a compact Kähler manifold and a
$X$
that is bimeromorphically equivalent to a compact Kähler manifold and a
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $X$
whose coefficients are in
$X$
whose coefficients are in
![]() $[0,1]\cap \mathbb{Q}$
such that
$[0,1]\cap \mathbb{Q}$
such that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier, that is, there exists a positive integer
$\mathbb{Q}$
-Cartier, that is, there exists a positive integer
![]() $m$
such that
$m$
such that
![]() $m\unicode[STIX]{x1D6E5}$
is integral and
$m\unicode[STIX]{x1D6E5}$
is integral and
![]() $(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(m\unicode[STIX]{x1D6E5}))^{\ast \ast }$
is locally free, where
$(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(m\unicode[STIX]{x1D6E5}))^{\ast \ast }$
is locally free, where
![]() $\unicode[STIX]{x1D714}_{X}$
is the canonical sheaf of
$\unicode[STIX]{x1D714}_{X}$
is the canonical sheaf of
![]() $X$
. In this paper, we establish the following theorem, which is a generalization of the minimal model theory for projective
$X$
. In this paper, we establish the following theorem, which is a generalization of the minimal model theory for projective
![]() $\mathbb{Q}$
-factorial log surfaces obtained in [Reference FujinoFn4] (for some related topics, see [Reference Fujino and TanakaFT], [Reference TanakaT], [Reference HashizumeHa1], [Reference LiuLi], [Reference MiyamotoMi], and [Reference FujinoFn7, Section 4.10]).
$\mathbb{Q}$
-factorial log surfaces obtained in [Reference FujinoFn4] (for some related topics, see [Reference Fujino and TanakaFT], [Reference TanakaT], [Reference HashizumeHa1], [Reference LiuLi], [Reference MiyamotoMi], and [Reference FujinoFn7, Section 4.10]).
Theorem 1.1. (Minimal model theory for
 $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
 ${\mathcal{C}}$
)
${\mathcal{C}}$
)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a
$(X,\unicode[STIX]{x1D6E5})$
be a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Then we can construct a finite sequence of projective bimeromorphic morphisms starting from
${\mathcal{C}}$
. Then we can construct a finite sequence of projective bimeromorphic morphisms starting from
![]() $(X,\unicode[STIX]{x1D6E5})$
:
$(X,\unicode[STIX]{x1D6E5})$
:
such that
![]() $(X_{i},\unicode[STIX]{x1D6E5}_{i})$
, where
$(X_{i},\unicode[STIX]{x1D6E5}_{i})$
, where
![]() $\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
, is a
$\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
, is a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
and that
${\mathcal{C}}$
and that
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
and
$\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
and
![]() $-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
$-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
![]() $i$
. The final model
$i$
. The final model
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
satisfies one of the following conditions.
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
satisfies one of the following conditions.
-
(i) (Good minimal model).
 $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample. -
(ii) (Mori fiber space). There exists a surjective morphism
 $g:X^{\ast }\rightarrow W$
onto a normal projective variety
$g:X^{\ast }\rightarrow W$
onto a normal projective variety
 $W$
with connected fibers such that
$W$
with connected fibers such that
 $-(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })$
is
$-(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })$
is
 $g$
-ample,
$g$
-ample,
 $\dim W<2$
, and the relative Picard number
$\dim W<2$
, and the relative Picard number
 $\unicode[STIX]{x1D70C}(X^{\ast }/W)$
is one.
$\unicode[STIX]{x1D70C}(X^{\ast }/W)$
is one.
We note that
-
(i) if
 $X_{i_{0}}$
is projective for some
$X_{i_{0}}$
is projective for some
 $i_{0}$
, then
$i_{0}$
, then
 $X_{i}$
is automatically projective for every
$X_{i}$
is automatically projective for every
 $i$
, and
$i$
, and -
(ii) if
 $X_{i_{0}}$
has only rational singularities for some
$X_{i_{0}}$
has only rational singularities for some
 $i_{0}$
, then all the singularities of
$i_{0}$
, then all the singularities of
 $X_{i}$
are rational for every
$X_{i}$
are rational for every
 $i$
.
$i$
.
We note that the above sequence of contraction morphisms is nothing but the minimal model program for projective
![]() $\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4] when
$\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4] when
![]() $X$
is projective and that
$X$
is projective and that
![]() $X$
is automatically projective when
$X$
is automatically projective when
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
or
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
or
![]() $2$
.
$2$
.
Theorem 1.1 is not difficult to check once we know the minimal model theory for projective
![]() $\mathbb{Q}$
-factorial log surfaces in [Reference FujinoFn4], the Enriques–Kodaira classification of compact complex surfaces (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]), and some basic results on complex analytic spaces. We note that Theorem 1.1 includes the abundance theorem for
$\mathbb{Q}$
-factorial log surfaces in [Reference FujinoFn4], the Enriques–Kodaira classification of compact complex surfaces (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]), and some basic results on complex analytic spaces. We note that Theorem 1.1 includes the abundance theorem for
![]() $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Theorem 1.2. (Abundance theorem for
 $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
 ${\mathcal{C}}$
; see Theorem 7.2)
${\mathcal{C}}$
; see Theorem 7.2)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a
$(X,\unicode[STIX]{x1D6E5})$
be a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. Then
$X$
. Then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
From the minimal model theoretic viewpoint, it is very natural to treat log canonical surfaces
![]() $(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
![]() ${\mathcal{C}}$
. Unfortunately,
${\mathcal{C}}$
. Unfortunately,
![]() $X$
is not necessarily
$X$
is not necessarily
![]() $\mathbb{Q}$
-factorial in this case. So we cannot directly apply Theorem 1.1 to log canonical surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial in this case. So we cannot directly apply Theorem 1.1 to log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
. In order to establish the minimal model theory for log canonical surfaces in Fujiki’s class
${\mathcal{C}}$
. In order to establish the minimal model theory for log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
, we prove the following theorem.
${\mathcal{C}}$
, we prove the following theorem.
Theorem 1.3. (Projectivity of log canonical surfaces in Fujiki’s class
 ${\mathcal{C}}$
with negative Kodaira dimension; see Theorem 9.1)
${\mathcal{C}}$
with negative Kodaira dimension; see Theorem 9.1)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Then
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Then
![]() $X$
is projective.
$X$
is projective.
The proof of Theorem 1.3 is much more difficult than we expected. We prove it with the aid of the classification of two-dimensional log canonical singularities. We note that there are nonprojective normal complete rational surfaces (see [Reference NagataNg, Section 4]). Fortunately, such surfaces do not appear under the assumption of Theorem 1.3. Since Nagata’s example in [Reference NagataNg, Section 4] is not log canonical, we explicitly construct some examples of complete nonprojective log canonical algebraic surfaces in Section 12 for the reader’s convenience. Our construction, which was suggested by Kento Fujita, is arguably simpler than Nagata’s original and classical one (see [Reference NagataNg, Section 4]). Here, we explain the most interesting example.
Example 1.4. (see Example 12.3)
There exists a complete nonprojective log canonical algebraic surface
![]() $S$
with
$S$
with
![]() $\operatorname{Pic}(S)=\{0\}$
and
$\operatorname{Pic}(S)=\{0\}$
and
![]() $K_{S}\sim 0$
. In particular,
$K_{S}\sim 0$
. In particular,
![]() $\unicode[STIX]{x1D705}(S,K_{S})=0$
holds.
$\unicode[STIX]{x1D705}(S,K_{S})=0$
holds.
For the details of Example 1.4 and some other examples of complete nonprojective algebraic surfaces, see Section 12, where the reader can find some examples of complete nonprojective log canonical algebraic surfaces
![]() $S$
with
$S$
with
![]() $\operatorname{Pic}(S)=\{0\}$
,
$\operatorname{Pic}(S)=\{0\}$
,
![]() $\overline{\operatorname{NE}}(S)=\mathbb{R}_{{\geqslant}0}$
, or
$\overline{\operatorname{NE}}(S)=\mathbb{R}_{{\geqslant}0}$
, or
![]() $\overline{\operatorname{NE}}(S)=N_{1}(S)$
.
$\overline{\operatorname{NE}}(S)=N_{1}(S)$
.
Thus, by using Theorem 1.3, we have the following minimal model theory for log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Theorem 1.5. (Minimal model theory for log canonical surfaces in Fujiki’s class
 ${\mathcal{C}}$
)
${\mathcal{C}}$
)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Then we can construct a finite sequence of projective bimeromorphic morphisms starting from
${\mathcal{C}}$
. Then we can construct a finite sequence of projective bimeromorphic morphisms starting from
![]() $(X,\unicode[STIX]{x1D6E5})$
:
$(X,\unicode[STIX]{x1D6E5})$
:
such that
![]() $(X_{i},\unicode[STIX]{x1D6E5}_{i})$
, where
$(X_{i},\unicode[STIX]{x1D6E5}_{i})$
, where
![]() $\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
, is a log canonical surface in Fujiki’s class
$\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
, is a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
and that
${\mathcal{C}}$
and that
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
and
$\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
and
![]() $-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
$-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
![]() $i$
. The final model
$i$
. The final model
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
satisfies one of the following conditions.
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
satisfies one of the following conditions.
-
(i) (Good minimal model).
 $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample. -
(ii) (Mori fiber space). There exists a surjective morphism
 $g:X^{\ast }\rightarrow W$
onto a normal projective variety
$g:X^{\ast }\rightarrow W$
onto a normal projective variety
 $W$
with connected fibers such that
$W$
with connected fibers such that
 $-(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })$
is
$-(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })$
is
 $g$
-ample,
$g$
-ample,
 $\dim W<2$
, and the relative Picard number
$\dim W<2$
, and the relative Picard number
 $\unicode[STIX]{x1D70C}(X^{\ast }/W)$
is one.
$\unicode[STIX]{x1D70C}(X^{\ast }/W)$
is one.
We note that
-
(1) if
 $X_{i_{0}}$
is projective for some
$X_{i_{0}}$
is projective for some
 $i_{0}$
, then
$i_{0}$
, then
 $X_{i}$
is automatically projective for every
$X_{i}$
is automatically projective for every
 $i$
,
$i$
, -
(2) if
 $X_{i_{0}}$
has only rational singularities for some
$X_{i_{0}}$
has only rational singularities for some
 $i_{0}$
, then all the singularities of
$i_{0}$
, then all the singularities of
 $X_{i}$
are rational for every
$X_{i}$
are rational for every
 $i$
, and
$i$
, and -
(3) if
 $X_{i_{0}}$
is
$X_{i_{0}}$
is
 $\mathbb{Q}$
-factorial for some
$\mathbb{Q}$
-factorial for some
 $i_{0}$
, then so is
$i_{0}$
, then so is
 $X_{i}$
for every
$X_{i}$
for every
 $i$
.
$i$
.
We note that the above sequence of contraction morphisms is nothing but the usual minimal model program for projective log canonical surfaces (see [Reference FujinoFn4]) when
![]() $X$
is projective and that
$X$
is projective and that
![]() $X$
is automatically projective when
$X$
is automatically projective when
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
by Theorem 1.3.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
by Theorem 1.3.
In a series of papers (see [Reference Höring and PeternellHP1], [Reference Höring and PeternellHP2], and [Reference Campana, Höring and PeternellCHP]), Campana, Höring, and Peternell established the minimal model program and the abundance theorem for Kähler threefolds (see also [Reference Höring and PeternellHP3]). Their approach is essentially analytic. On the other hand, our approach is much more elementary than theirs and is not analytic. Although we mainly treat compact analytic surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
, we do not discuss Kähler forms (or currents) on singular surfaces (see [Reference FujikiFk]).
${\mathcal{C}}$
, we do not discuss Kähler forms (or currents) on singular surfaces (see [Reference FujikiFk]).
In Section 11, we treat some vanishing theorems for proper bimeromorphic morphisms between analytic surfaces. They play an important role in this paper. Although they are more or less known to the experts, we explain the details for the reader’s convenience because we can find no suitable references. We think that the results are useful for other applications. The most useful formulation is Theorem 11.3(2).
Theorem 1.6. (see Theorem 11.3)
Let
![]() $X$
be a normal analytic surface and let
$X$
be a normal analytic surface and let
![]() $\unicode[STIX]{x1D6E5}$
be an effective
$\unicode[STIX]{x1D6E5}$
be an effective
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
whose coefficients are less than one such that
$X$
whose coefficients are less than one such that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier. Let
$\mathbb{Q}$
-Cartier. Let
![]() $f:X\rightarrow Y$
be a proper bimeromorphic morphism onto a normal analytic surface
$f:X\rightarrow Y$
be a proper bimeromorphic morphism onto a normal analytic surface
![]() $Y$
. Let
$Y$
. Let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
, and let
$X$
, and let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-Cartier Weil divisor on
$\mathbb{Q}$
-Cartier Weil divisor on
![]() $X$
. Assume that
$X$
. Assume that
![]() ${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C\geqslant 0$
for every
${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C\geqslant 0$
for every
![]() $f$
-exceptional curve
$f$
-exceptional curve
![]() $C$
on
$C$
on
![]() $X$
. Then
$X$
. Then
![]() $R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
holds for every
$R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
holds for every
![]() $i>0$
.
$i>0$
.
We explain the organization of this paper. In Section 2, we collect some basic definitions and results. In Section 3, we explain a very easy version of the basepoint-free theorem for projective bimeromorphic morphisms between surfaces (see Theorem 3.11). In Section 4, we collect some useful projectivity criteria for
![]() $\mathbb{Q}$
-factorial compact analytic surfaces. In Section 5, we discuss the minimal model program for
$\mathbb{Q}$
-factorial compact analytic surfaces. In Section 5, we discuss the minimal model program for
![]() $\mathbb{Q}$
-factorial log surfaces based on Sakai’s contraction theorem, which is a slight generalization of Grauert’s famous contraction theorem. Then we prove Theorem 1.1 except for the semiampleness of
$\mathbb{Q}$
-factorial log surfaces based on Sakai’s contraction theorem, which is a slight generalization of Grauert’s famous contraction theorem. Then we prove Theorem 1.1 except for the semiampleness of
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
. In Section 6, we briefly discuss the finite generation of log canonical rings of
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
. In Section 6, we briefly discuss the finite generation of log canonical rings of
![]() $\mathbb{Q}$
-factorial log surfaces, which is essentially contained in [Reference FujinoFn4], and some related topics. In Section 7, we prove the nonvanishing theorem and the abundance theorem. Precisely speaking, we explain how to modify the arguments in [Reference FujinoFn4] for
$\mathbb{Q}$
-factorial log surfaces, which is essentially contained in [Reference FujinoFn4], and some related topics. In Section 7, we prove the nonvanishing theorem and the abundance theorem. Precisely speaking, we explain how to modify the arguments in [Reference FujinoFn4] for
![]() $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
. In Section 8, we discuss a contraction theorem for log canonical surfaces. A key point is that the exceptional curve automatically becomes
${\mathcal{C}}$
. In Section 8, we discuss a contraction theorem for log canonical surfaces. A key point is that the exceptional curve automatically becomes
![]() $\mathbb{Q}$
-Cartier. This simple fact plays a crucial role in our minimal model theory for log canonical surfaces. Section 9 is devoted to the proof of Theorem 1.3, that is, the projectivity of log canonical surfaces in Fujiki’s class
$\mathbb{Q}$
-Cartier. This simple fact plays a crucial role in our minimal model theory for log canonical surfaces. Section 9 is devoted to the proof of Theorem 1.3, that is, the projectivity of log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
with negative Kodaira dimension. Our proof needs the classification of two-dimensional log canonical singularities. In Section 10, we prove Theorem 1.5, that is, the minimal model theory for log canonical surfaces in Fujiki’s class
${\mathcal{C}}$
with negative Kodaira dimension. Our proof needs the classification of two-dimensional log canonical singularities. In Section 10, we prove Theorem 1.5, that is, the minimal model theory for log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
. In Section 11, we discuss some vanishing theorems for proper bimeromorphic morphisms between normal analytic surfaces. Fortunately, we need no deep analytic methods except for the theorem on formal functions for proper morphisms between analytic spaces. In Section 12, we construct some complete nonprojective log canonical algebraic surfaces.
${\mathcal{C}}$
. In Section 11, we discuss some vanishing theorems for proper bimeromorphic morphisms between normal analytic surfaces. Fortunately, we need no deep analytic methods except for the theorem on formal functions for proper morphisms between analytic spaces. In Section 12, we construct some complete nonprojective log canonical algebraic surfaces.
We will use the minimal model theory for projective log surfaces defined over
![]() $\mathbb{C}$
, the complex number field, established in [Reference FujinoFn4]. We will freely use the basic notation of the minimal model theory as in [Reference FujinoFn3] and [Reference FujinoFn7].
$\mathbb{C}$
, the complex number field, established in [Reference FujinoFn4]. We will freely use the basic notation of the minimal model theory as in [Reference FujinoFn3] and [Reference FujinoFn7].
2 Preliminaries
In this section, we collect some basic definitions and results.
Definition 2.1. (Boundary and subboundary
 $\mathbb{Q}$
-divisors)
$\mathbb{Q}$
-divisors)
Let
![]() $X$
be an irreducible normal analytic space and let
$X$
be an irreducible normal analytic space and let
![]() $\unicode[STIX]{x1D6E5}$
be a
$\unicode[STIX]{x1D6E5}$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. If the coefficients of
$X$
. If the coefficients of
![]() $\unicode[STIX]{x1D6E5}$
are in
$\unicode[STIX]{x1D6E5}$
are in
![]() $[0,1]\cap \mathbb{Q}$
(resp.
$[0,1]\cap \mathbb{Q}$
(resp.
![]() $(-\infty ,1]\cap \mathbb{Q}$
), then
$(-\infty ,1]\cap \mathbb{Q}$
), then
![]() $\unicode[STIX]{x1D6E5}$
is called a boundary (resp. subboundary)
$\unicode[STIX]{x1D6E5}$
is called a boundary (resp. subboundary)
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
.
$X$
.
Definition 2.2. (Operations for
 $\mathbb{Q}$
-divisors)
$\mathbb{Q}$
-divisors)
Let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-divisor on a normal analytic space. Then
$\mathbb{Q}$
-divisor on a normal analytic space. Then
![]() $\lceil D\rceil$
(resp.
$\lceil D\rceil$
(resp.
![]() $\lfloor D\rfloor$
) denotes the round-up (resp. round-down) of
$\lfloor D\rfloor$
) denotes the round-up (resp. round-down) of
![]() $D$
. We put
$D$
. We put
![]() $\{D\}:=D-\lfloor D\rfloor$
and call it the fractional part of
$\{D\}:=D-\lfloor D\rfloor$
and call it the fractional part of
![]() $D$
.
$D$
.
Definition 2.3. (Algebraic dimensions)
Let
![]() $X$
be an irreducible compact analytic space. Let
$X$
be an irreducible compact analytic space. Let
![]() ${\mathcal{M}}(X)$
be the field of meromorphic functions on
${\mathcal{M}}(X)$
be the field of meromorphic functions on
![]() $X$
. Then the transcendence degree of
$X$
. Then the transcendence degree of
![]() ${\mathcal{M}}(X)$
over
${\mathcal{M}}(X)$
over
![]() $\mathbb{C}$
is called the algebraic dimension of
$\mathbb{C}$
is called the algebraic dimension of
![]() $X$
and is denoted by
$X$
and is denoted by
![]() $a(X)$
. It is well known that
$a(X)$
. It is well known that
![]() $0\leqslant a(X)\leqslant \dim X$
holds. If
$0\leqslant a(X)\leqslant \dim X$
holds. If
![]() $a(X)=\dim X$
holds, then we say that
$a(X)=\dim X$
holds, then we say that
![]() $X$
is Moishezon. We note that if
$X$
is Moishezon. We note that if
![]() $X$
is Moishezon, then
$X$
is Moishezon, then
![]() $X$
is an algebraic space, which is proper over
$X$
is an algebraic space, which is proper over
![]() $\mathbb{C}$
(see [Reference UenoU, Remark 3.7]).
$\mathbb{C}$
(see [Reference UenoU, Remark 3.7]).
For the basic properties of
![]() $a(X)$
, we recommend the reader to see [Reference UenoU, Section 3].
$a(X)$
, we recommend the reader to see [Reference UenoU, Section 3].
Definition 2.4. Let
![]() $X$
be an irreducible compact normal analytic space such that
$X$
be an irreducible compact normal analytic space such that
![]() $X$
is Moishezon. Then we can obtain the perfect pairing
$X$
is Moishezon. Then we can obtain the perfect pairing
induced from the intersection pairing of curves and line bundles as in the case where
![]() $X$
is projective. We note that
$X$
is projective. We note that
![]() $\unicode[STIX]{x1D70C}(X):=\dim _{\mathbb{R}}N^{1}(X)<\infty$
always holds. We call
$\unicode[STIX]{x1D70C}(X):=\dim _{\mathbb{R}}N^{1}(X)<\infty$
always holds. We call
![]() $\unicode[STIX]{x1D70C}(X)$
the Picard number of
$\unicode[STIX]{x1D70C}(X)$
the Picard number of
![]() $X$
. When
$X$
. When
![]() $X$
is an algebraic variety,
$X$
is an algebraic variety,
![]() $\overline{\operatorname{NE}}(X)$
(
$\overline{\operatorname{NE}}(X)$
(
![]() $\subset N_{1}(X)$
) denotes the Kleiman–Mori cone of
$\subset N_{1}(X)$
) denotes the Kleiman–Mori cone of
![]() $X$
.
$X$
.
In this paper, we do not consider
![]() $N_{1}(X)$
when
$N_{1}(X)$
when
![]() $0\leqslant a(X)<\dim X$
. When
$0\leqslant a(X)<\dim X$
. When
![]() $X$
is a complete nonprojective singular algebraic variety,
$X$
is a complete nonprojective singular algebraic variety,
![]() $\overline{\operatorname{NE}}(X)$
does not always behave well (see [Reference FujinoFn1], [Reference Fujino and PayneFP], and Section 12).
$\overline{\operatorname{NE}}(X)$
does not always behave well (see [Reference FujinoFn1], [Reference Fujino and PayneFP], and Section 12).
Remark 2.5. Let
![]() $X$
be a compact smooth analytic surface whose algebraic dimension
$X$
be a compact smooth analytic surface whose algebraic dimension
![]() $a(X)$
is zero. Then it is well known that there are only finitely many curves on
$a(X)$
is zero. Then it is well known that there are only finitely many curves on
![]() $X$
(see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter IV, (8.2) Theorem]).
$X$
(see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter IV, (8.2) Theorem]).
In the subsequent sections, we will repeatedly use the following well-known negativity lemma and its consequences without mentioning them explicitly. For the proof of Lemma 2.6, see [Reference MatsukiMa, Theorem 4-6-1].
Lemma 2.6. (Negativity lemma)
Let
![]() $P\in Y$
be a germ of normal analytic surface, and let
$P\in Y$
be a germ of normal analytic surface, and let
![]() $f:X\rightarrow Y$
be a proper bimeromorphic morphism from a smooth analytic surface
$f:X\rightarrow Y$
be a proper bimeromorphic morphism from a smooth analytic surface
![]() $X$
. Then
$X$
. Then
![]() $f^{-1}(P)$
is connected and has a negative definite intersection form.
$f^{-1}(P)$
is connected and has a negative definite intersection form.
Let us quickly recall the definition of the Iitaka dimension
![]() $\unicode[STIX]{x1D705}$
. For the details of
$\unicode[STIX]{x1D705}$
. For the details of
![]() $\unicode[STIX]{x1D705}$
, see [Reference NakayamaNk] and [Reference UenoU].
$\unicode[STIX]{x1D705}$
, see [Reference NakayamaNk] and [Reference UenoU].
Definition 2.7. (Iitaka dimensions)
Let
![]() $X$
be an irreducible compact normal analytic space, and let
$X$
be an irreducible compact normal analytic space, and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
. Then we set
$X$
. Then we set
and call it the Iitaka dimension of
![]() ${\mathcal{L}}$
. It is well known that
${\mathcal{L}}$
. It is well known that
holds. We can define
![]() $\unicode[STIX]{x1D705}(X,D)$
for
$\unicode[STIX]{x1D705}(X,D)$
for
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisors
$\mathbb{Q}$
-divisors
![]() $D$
on
$D$
on
![]() $X$
similarly.
$X$
similarly.
We close this section with an easy lemma on rational singularities.
Lemma 2.8. (see [Reference FujinoFn6, Lemma 3.1])
Let
![]() $\unicode[STIX]{x1D711}:X\rightarrow Y$
be a proper bimeromorphic morphism between normal analytic spaces. If
$\unicode[STIX]{x1D711}:X\rightarrow Y$
be a proper bimeromorphic morphism between normal analytic spaces. If
![]() $R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
for every
$R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
for every
![]() $i>0$
, then
$i>0$
, then
![]() $X$
has only rational singularities if and only if so does
$X$
has only rational singularities if and only if so does
![]() $Y$
.
$Y$
.
Proof. The problem is local. So we can freely shrink
![]() $Y$
around an arbitrary given point. Let us consider a common resolution:
$Y$
around an arbitrary given point. Let us consider a common resolution:

By assumption and the Leray spectral sequence, we have
![]() $R^{i}p_{\ast }{\mathcal{O}}_{W}\simeq R^{i}q_{\ast }{\mathcal{O}}_{W}$
for every
$R^{i}p_{\ast }{\mathcal{O}}_{W}\simeq R^{i}q_{\ast }{\mathcal{O}}_{W}$
for every
![]() $i$
. This implies the desired statement.◻
$i$
. This implies the desired statement.◻
3 Log surfaces
In this section, we define
![]() $\mathbb{Q}$
-factorial log surfaces and log canonical surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces and log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
and discuss a very easy version of the basepoint-free theorem for proper bimeromorphic morphisms between normal analytic surfaces.
${\mathcal{C}}$
and discuss a very easy version of the basepoint-free theorem for proper bimeromorphic morphisms between normal analytic surfaces.
In this paper, we adopt the following definition of analytic spaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Definition 3.1. (Fujiki’s class
 ${\mathcal{C}}$
)
${\mathcal{C}}$
)
Let
![]() $X$
be an irreducible compact analytic space. If
$X$
be an irreducible compact analytic space. If
![]() $X$
is bimeromorphically equivalent to a compact Kähler manifold, then we say that
$X$
is bimeromorphically equivalent to a compact Kähler manifold, then we say that
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Remark 3.2. Let
![]() $X$
be an irreducible compact analytic space. We note that if
$X$
be an irreducible compact analytic space. We note that if
![]() $X$
is Moishezon, then
$X$
is Moishezon, then
![]() $X$
is automatically in Fujiki’s class
$X$
is automatically in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
We have a useful characterization of surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Lemma 3.3. Let
![]() $X$
be an irreducible compact normal analytic surface. Then
$X$
be an irreducible compact normal analytic surface. Then
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
if and only if there exists a resolution of singularities
${\mathcal{C}}$
if and only if there exists a resolution of singularities
![]() $f:Y\rightarrow X$
such that
$f:Y\rightarrow X$
such that
![]() $Y$
is Kähler, that is,
$Y$
is Kähler, that is,
![]() $Y$
is a two-dimensional compact Kähler manifold and
$Y$
is a two-dimensional compact Kähler manifold and
![]() $f$
is a bimeromorphic morphism.
$f$
is a bimeromorphic morphism.
Proof. Note that a compact smooth analytic surface
![]() $S$
is Kähler if and only if the first Betti number
$S$
is Kähler if and only if the first Betti number
![]() $b_{1}(S)$
is even (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter IV, (3.1) Theorem]). We also note that the first Betti number is preserved under blow-ups. Thus we can easily check the statement.◻
$b_{1}(S)$
is even (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter IV, (3.1) Theorem]). We also note that the first Betti number is preserved under blow-ups. Thus we can easily check the statement.◻
As an easy consequence of Lemma 3.3 and its proof, we have the following corollary.
Corollary 3.4. Let
![]() $X$
be a compact normal analytic surface in Fujiki’s class
$X$
be a compact normal analytic surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Let
${\mathcal{C}}$
. Let
![]() $f:Y\rightarrow X$
be any resolution of singularities. Then
$f:Y\rightarrow X$
be any resolution of singularities. Then
![]() $Y$
is a compact Kähler manifold.
$Y$
is a compact Kähler manifold.
Let us define canonical sheaves.
Definition 3.5. (Canonical sheaves)
Let
![]() $X$
be a normal analytic surface and let
$X$
be a normal analytic surface and let
![]() $\text{Sing}X$
denote the singular locus of
$\text{Sing}X$
denote the singular locus of
![]() $X$
. Then we have
$X$
. Then we have
![]() $\text{codim}_{X}\text{Sing}X\geqslant 2$
since
$\text{codim}_{X}\text{Sing}X\geqslant 2$
since
![]() $X$
is normal. Let
$X$
is normal. Let
![]() $\unicode[STIX]{x1D714}_{U}$
be the canonical bundle of
$\unicode[STIX]{x1D714}_{U}$
be the canonical bundle of
![]() $U:=X\setminus \text{Sing}X$
. We put
$U:=X\setminus \text{Sing}X$
. We put
![]() $\unicode[STIX]{x1D714}_{X}:=\unicode[STIX]{x1D704}_{\ast }\{_{U}$
, where
$\unicode[STIX]{x1D714}_{X}:=\unicode[STIX]{x1D704}_{\ast }\{_{U}$
, where
![]() $\unicode[STIX]{x1D704}:U{\hookrightarrow}X$
is the natural open immersion, and call
$\unicode[STIX]{x1D704}:U{\hookrightarrow}X$
is the natural open immersion, and call
![]() $\unicode[STIX]{x1D714}_{X}$
the canonical sheaf of
$\unicode[STIX]{x1D714}_{X}$
the canonical sheaf of
![]() $X$
.
$X$
.
Remark 3.6. Some normal analytic surface
![]() $X$
does not admit any nonzero meromorphic section of
$X$
does not admit any nonzero meromorphic section of
![]() $\unicode[STIX]{x1D714}_{X}$
. However, if there is no risk of confusion, we use the symbol
$\unicode[STIX]{x1D714}_{X}$
. However, if there is no risk of confusion, we use the symbol
![]() $K_{X}$
as a formal divisor class with an isomorphism
$K_{X}$
as a formal divisor class with an isomorphism
![]() ${\mathcal{O}}_{X}(K_{X})\simeq \unicode[STIX]{x1D714}_{X}$
and call it the canonical divisor of
${\mathcal{O}}_{X}(K_{X})\simeq \unicode[STIX]{x1D714}_{X}$
and call it the canonical divisor of
![]() $X$
.
$X$
.
In this paper, we adopt the following definition of log surfaces.
Definition 3.7. (Log surfaces)
Let
![]() $X$
be an irreducible compact normal analytic surface, and let
$X$
be an irreducible compact normal analytic surface, and let
![]() $\unicode[STIX]{x1D6E5}$
be a boundary
$\unicode[STIX]{x1D6E5}$
be a boundary
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Assume that
$X$
. Assume that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier. Note that this means that there exists a positive integer
$\mathbb{Q}$
-Cartier. Note that this means that there exists a positive integer
![]() $m$
such that
$m$
such that
![]() $m\unicode[STIX]{x1D6E5}$
is integral and that
$m\unicode[STIX]{x1D6E5}$
is integral and that
![]() $(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(m\unicode[STIX]{x1D6E5}))^{\ast \ast }$
is locally free. Then the pair
$(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(m\unicode[STIX]{x1D6E5}))^{\ast \ast }$
is locally free. Then the pair
![]() $(X,\unicode[STIX]{x1D6E5})$
is called a log surface. We say that a log surface
$(X,\unicode[STIX]{x1D6E5})$
is called a log surface. We say that a log surface
![]() $(X,\unicode[STIX]{x1D6E5})$
is in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
is in Fujiki’s class
![]() ${\mathcal{C}}$
when
${\mathcal{C}}$
when
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
. Let
${\mathcal{C}}$
. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log surface. Then we usually call
$(X,\unicode[STIX]{x1D6E5})$
be a log surface. Then we usually call
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})$
the Kodaira dimension of
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})$
the Kodaira dimension of
![]() $(X,\unicode[STIX]{x1D6E5})$
.
$(X,\unicode[STIX]{x1D6E5})$
.
We need to define log canonical surfaces.
Definition 3.8. (Log canonical surfaces)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log surface, and let
$(X,\unicode[STIX]{x1D6E5})$
be a log surface, and let
![]() $f:Y\rightarrow X$
be a proper bimeromorphic morphism from a smooth analytic surface
$f:Y\rightarrow X$
be a proper bimeromorphic morphism from a smooth analytic surface
![]() $Y$
. Then we can write
$Y$
. Then we can write
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
with
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
with
![]() $f_{\ast }\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D6E5}$
. If the coefficients of
$f_{\ast }\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D6E5}$
. If the coefficients of
![]() $\unicode[STIX]{x1D6E5}_{Y}$
are less than or equal to one for every
$\unicode[STIX]{x1D6E5}_{Y}$
are less than or equal to one for every
![]() $f:Y\rightarrow X$
, then
$f:Y\rightarrow X$
, then
![]() $(X,\unicode[STIX]{x1D6E5})$
is called a log canonical surface.
$(X,\unicode[STIX]{x1D6E5})$
is called a log canonical surface.
The notion of
![]() $\mathbb{Q}$
-factoriality plays a crucial role in this paper.
$\mathbb{Q}$
-factoriality plays a crucial role in this paper.
Definition 3.9. (
 $\mathbb{Q}$
-factoriality)
$\mathbb{Q}$
-factoriality)
Let
![]() $X$
be an irreducible compact normal analytic surface, and let
$X$
be an irreducible compact normal analytic surface, and let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Then we say that
$X$
. Then we say that
![]() $D$
is
$D$
is
![]() $\mathbb{Q}$
-Cartier if there exists a positive integer
$\mathbb{Q}$
-Cartier if there exists a positive integer
![]() $m$
such that
$m$
such that
![]() $mD$
is Cartier. If every Weil divisor on
$mD$
is Cartier. If every Weil divisor on
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-Cartier, then we say that
$\mathbb{Q}$
-Cartier, then we say that
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Lemma 3.10 is well known.
Lemma 3.10. Let
![]() $X$
be an irreducible compact normal analytic surface. Assume that
$X$
be an irreducible compact normal analytic surface. Assume that
![]() $X$
has only rational singularities. Then
$X$
has only rational singularities. Then
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Proof. This follows from [Reference NakayamaNk, Chapter II, 2.12. Lemma]. ◻
We close this section with a very easy version of the basepoint-free theorem for projective bimeromorphic morphisms between normal analytic surfaces (see also Remark 11.4).
Theorem 3.11. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log surface and let
$(X,\unicode[STIX]{x1D6E5})$
be a log surface and let
![]() $\unicode[STIX]{x1D711}:X\rightarrow Y$
be a projective bimeromorphic morphism onto a normal analytic surface
$\unicode[STIX]{x1D711}:X\rightarrow Y$
be a projective bimeromorphic morphism onto a normal analytic surface
![]() $Y$
. Assume that
$Y$
. Assume that
![]() $C:=\operatorname{Exc}(\unicode[STIX]{x1D711})$
is
$C:=\operatorname{Exc}(\unicode[STIX]{x1D711})$
is
![]() $\mathbb{Q}$
-Cartier,
$\mathbb{Q}$
-Cartier,
![]() $C\simeq \mathbb{P}^{1}$
, and
$C\simeq \mathbb{P}^{1}$
, and
![]() $-C$
and
$-C$
and
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})$
are
$-(K_{X}+\unicode[STIX]{x1D6E5})$
are
![]() $\unicode[STIX]{x1D711}$
-ample. Let
$\unicode[STIX]{x1D711}$
-ample. Let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
with
$X$
with
![]() ${\mathcal{L}}\cdot C=0$
. Then there exists a line bundle
${\mathcal{L}}\cdot C=0$
. Then there exists a line bundle
![]() ${\mathcal{L}}_{Y}$
on
${\mathcal{L}}_{Y}$
on
![]() $Y$
such that
$Y$
such that
![]() ${\mathcal{L}}\simeq \unicode[STIX]{x1D711}^{\ast }{\mathcal{L}}_{Y}$
holds. In particular,
${\mathcal{L}}\simeq \unicode[STIX]{x1D711}^{\ast }{\mathcal{L}}_{Y}$
holds. In particular,
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial if and only if so is
$\mathbb{Q}$
-factorial if and only if so is
![]() $Y$
.
$Y$
.
Proof. In Step 1, we will prove the existence of
![]() ${\mathcal{L}}_{Y}$
. In Steps 2 and 3, we will see that
${\mathcal{L}}_{Y}$
. In Steps 2 and 3, we will see that
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial if and only if so is
$\mathbb{Q}$
-factorial if and only if so is
![]() $Y$
.
$Y$
.
Step 1. Since
![]() $C\simeq \mathbb{P}^{1}$
and
$C\simeq \mathbb{P}^{1}$
and
![]() ${\mathcal{L}}\cdot C=0$
,
${\mathcal{L}}\cdot C=0$
,
![]() ${\mathcal{L}}|_{C}$
is trivial. Since
${\mathcal{L}}|_{C}$
is trivial. Since
![]() $-C$
and
$-C$
and
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})$
are
$-(K_{X}+\unicode[STIX]{x1D6E5})$
are
![]() $\unicode[STIX]{x1D711}$
-ample, we may assume that
$\unicode[STIX]{x1D711}$
-ample, we may assume that
![]() $C\leqslant \unicode[STIX]{x1D6E5}$
by increasing the coefficient of
$C\leqslant \unicode[STIX]{x1D6E5}$
by increasing the coefficient of
![]() $C$
in
$C$
in
![]() $\unicode[STIX]{x1D6E5}$
. Let us consider the following short exact sequence:
$\unicode[STIX]{x1D6E5}$
. Let us consider the following short exact sequence:
Note that
holds. Therefore, by Theorem 11.3, we get
![]() $R^{1}\unicode[STIX]{x1D711}_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(-C))=0$
. Thus, we have the following short exact sequence:
$R^{1}\unicode[STIX]{x1D711}_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(-C))=0$
. Thus, we have the following short exact sequence:
We note that
By (3.1),
![]() ${\mathcal{L}}$
is
${\mathcal{L}}$
is
![]() $\unicode[STIX]{x1D711}$
-free since
$\unicode[STIX]{x1D711}$
-free since
![]() ${\mathcal{L}}|_{C}$
is trivial. We note that
${\mathcal{L}}|_{C}$
is trivial. We note that
![]() $\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}\simeq {\mathcal{O}}_{Y}$
since
$\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}\simeq {\mathcal{O}}_{Y}$
since
![]() $Y$
is normal and
$Y$
is normal and
![]() $\unicode[STIX]{x1D711}$
has connected fibers. Thus
$\unicode[STIX]{x1D711}$
has connected fibers. Thus
![]() ${\mathcal{L}}_{Y}:=\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}$
is a line bundle on
${\mathcal{L}}_{Y}:=\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}$
is a line bundle on
![]() $Y$
such that
$Y$
such that
![]() ${\mathcal{L}}\simeq \unicode[STIX]{x1D711}^{\ast }{\mathcal{L}}_{Y}$
holds.
${\mathcal{L}}\simeq \unicode[STIX]{x1D711}^{\ast }{\mathcal{L}}_{Y}$
holds.
Step 2. Assume that
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial. We take a prime divisor
$\mathbb{Q}$
-factorial. We take a prime divisor
![]() $D$
on
$D$
on
![]() $Y$
. Let
$Y$
. Let
![]() $D^{\prime }$
be the strict transform of
$D^{\prime }$
be the strict transform of
![]() $D$
on
$D$
on
![]() $X$
. Then we can take
$X$
. Then we can take
![]() $a\in \mathbb{Q}$
and a divisible positive integer
$a\in \mathbb{Q}$
and a divisible positive integer
![]() $m$
such that
$m$
such that
![]() $m(D^{\prime }+aC)$
is Cartier and
$m(D^{\prime }+aC)$
is Cartier and
![]() $m(D^{\prime }+aC)\cdot C=0$
. We put
$m(D^{\prime }+aC)\cdot C=0$
. We put
![]() ${\mathcal{L}}={\mathcal{O}}_{X}(m(D^{\prime }+aC))$
and apply the result obtained in Step 1 to
${\mathcal{L}}={\mathcal{O}}_{X}(m(D^{\prime }+aC))$
and apply the result obtained in Step 1 to
![]() ${\mathcal{L}}$
. Then
${\mathcal{L}}$
. Then
![]() $mD=\unicode[STIX]{x1D711}_{\ast }(m(D^{\prime }+aC))$
is Cartier. This means that
$mD=\unicode[STIX]{x1D711}_{\ast }(m(D^{\prime }+aC))$
is Cartier. This means that
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Step 3. Assume that
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial. We take a prime divisor
$\mathbb{Q}$
-factorial. We take a prime divisor
![]() $D$
on
$D$
on
![]() $X$
. Then
$X$
. Then
![]() $D^{\prime }:=\unicode[STIX]{x1D711}_{\ast }D$
is a
$D^{\prime }:=\unicode[STIX]{x1D711}_{\ast }D$
is a
![]() $\mathbb{Q}$
-Cartier prime divisor on
$\mathbb{Q}$
-Cartier prime divisor on
![]() $Y$
. Since
$Y$
. Since
![]() $D=\unicode[STIX]{x1D711}^{\ast }D^{\prime }-aC$
holds for some
$D=\unicode[STIX]{x1D711}^{\ast }D^{\prime }-aC$
holds for some
![]() $a\in \mathbb{Q}$
,
$a\in \mathbb{Q}$
,
![]() $D$
is
$D$
is
![]() $\mathbb{Q}$
-Cartier. Therefore,
$\mathbb{Q}$
-Cartier. Therefore,
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
We complete the proof of Theorem 3.11. ◻
4 Projectivity criteria
Let us start with an easy but very useful projectivity criterion.
Lemma 4.1. (Projectivity of
 $\mathbb{Q}$
-factorial compact analytic surfaces)
$\mathbb{Q}$
-factorial compact analytic surfaces)
Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-factorial compact analytic surface. Assume that the algebraic dimension
$\mathbb{Q}$
-factorial compact analytic surface. Assume that the algebraic dimension
![]() $a(X)$
of
$a(X)$
of
![]() $X$
is two, that is,
$X$
is two, that is,
![]() $X$
is Moishezon. Then
$X$
is Moishezon. Then
![]() $X$
is projective.
$X$
is projective.
Proof. By the assumption
![]() $a(X)=2$
, we can construct a proper bimeromorphic morphism
$a(X)=2$
, we can construct a proper bimeromorphic morphism
![]() $f:Y\rightarrow X$
from a smooth projective surface
$f:Y\rightarrow X$
from a smooth projective surface
![]() $Y$
. By the assumption
$Y$
. By the assumption
![]() $a(X)=2$
again,
$a(X)=2$
again,
![]() $X$
is an algebraic space that is proper over
$X$
is an algebraic space that is proper over
![]() $\mathbb{C}$
by Artin’s GAGA (see [Reference UenoU, Remark 3.7]). We take a very ample effective Cartier divisor
$\mathbb{C}$
by Artin’s GAGA (see [Reference UenoU, Remark 3.7]). We take a very ample effective Cartier divisor
![]() $H$
on
$H$
on
![]() $Y$
. We put
$Y$
. We put
![]() $A=f_{\ast }H$
. Since
$A=f_{\ast }H$
. Since
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial,
$\mathbb{Q}$
-factorial,
![]() $A$
is a
$A$
is a
![]() $\mathbb{Q}$
-Cartier divisor. Then we have
$\mathbb{Q}$
-Cartier divisor. Then we have
![]() $A\cdot C=H\cdot f^{\ast }C>0$
for every curve
$A\cdot C=H\cdot f^{\ast }C>0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. In particular, we have
$X$
. In particular, we have
![]() $A^{2}>0$
. Therefore,
$A^{2}>0$
. Therefore,
![]() $A$
is ample by Nakai–Moishezon’s ampleness criterion for algebraic spaces (see [Reference Pascul GainzaP, (1.4) Theorem]). This implies that
$A$
is ample by Nakai–Moishezon’s ampleness criterion for algebraic spaces (see [Reference Pascul GainzaP, (1.4) Theorem]). This implies that
![]() $X$
is projective.◻
$X$
is projective.◻
The following corollary is obvious by Lemma 4.1.
Corollary 4.2. Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-factorial compact analytic surface. Assume that there exists a line bundle
$\mathbb{Q}$
-factorial compact analytic surface. Assume that there exists a line bundle
![]() ${\mathcal{L}}$
such that
${\mathcal{L}}$
such that
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})=2$
, that is,
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})=2$
, that is,
![]() ${\mathcal{L}}$
is a big line bundle. Then
${\mathcal{L}}$
is a big line bundle. Then
![]() $X$
is projective.
$X$
is projective.
Proof. By the assumption that
![]() ${\mathcal{L}}$
is big, we see that the algebraic dimension
${\mathcal{L}}$
is big, we see that the algebraic dimension
![]() $a(X)$
of
$a(X)$
of
![]() $X$
is two. Therefore,
$X$
is two. Therefore,
![]() $X$
is projective by Lemma 4.1.◻
$X$
is projective by Lemma 4.1.◻
By Corollary 4.2, the minimal model theory for projective
![]() $\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4] works for
$\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4] works for
![]() $(X,\unicode[STIX]{x1D6E5})$
with
$(X,\unicode[STIX]{x1D6E5})$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
in Theorem 1.1.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
in Theorem 1.1.
By combining Lemma 4.1 with the Enriques–Kodaira classification, we obtain the following projectivity criterion.
Lemma 4.3. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a
$(X,\unicode[STIX]{x1D6E5})$
be a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
. Then
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
. Then
![]() $X$
is projective.
$X$
is projective.
Proof. We take the minimal resolution
![]() $f:Y\rightarrow X$
. We put
$f:Y\rightarrow X$
. We put
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then we see that
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then we see that
![]() $\unicode[STIX]{x1D6E5}_{Y}$
is effective by the negativity lemma and that
$\unicode[STIX]{x1D6E5}_{Y}$
is effective by the negativity lemma and that
![]() $\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{Y})=\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Therefore, we obtain
$\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{Y})=\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Therefore, we obtain
![]() $\unicode[STIX]{x1D705}(Y,K_{Y})=-\infty$
by
$\unicode[STIX]{x1D705}(Y,K_{Y})=-\infty$
by
![]() $\unicode[STIX]{x1D705}(Y,K_{Y})\leqslant \unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{Y})=-\infty$
. Since
$\unicode[STIX]{x1D705}(Y,K_{Y})\leqslant \unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{Y})=-\infty$
. Since
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
, the first Betti number
${\mathcal{C}}$
, the first Betti number
![]() $b_{1}(Y)$
of
$b_{1}(Y)$
of
![]() $Y$
is even. Therefore, by the Enriques–Kodaira classification (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]),
$Y$
is even. Therefore, by the Enriques–Kodaira classification (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]),
![]() $Y$
is a smooth projective surface. Thus, by Lemma 4.1,
$Y$
is a smooth projective surface. Thus, by Lemma 4.1,
![]() $X$
is projective.◻
$X$
is projective.◻
We will repeatedly use the above projectivity criteria throughout this paper.
We note that the statement of Theorem 1.3 looks very similar to that of Lemma 4.3. However, a log canonical surface is not necessarily
![]() $\mathbb{Q}$
-factorial. Therefore, Theorem 1.3 is much harder to prove than Lemma 4.3 (see Section 9).
$\mathbb{Q}$
-factorial. Therefore, Theorem 1.3 is much harder to prove than Lemma 4.3 (see Section 9).
5 Minimal model program for
 $\mathbb{Q}$
-factorial log surfaces
$\mathbb{Q}$
-factorial log surfaces
By repeatedly using Grauert’s contraction theorem, we can easily run a kind of the minimal model program for
![]() $\mathbb{Q}$
-factorial log surfaces
$\mathbb{Q}$
-factorial log surfaces
![]() $(X,\unicode[STIX]{x1D6E5})$
. We note that
$(X,\unicode[STIX]{x1D6E5})$
. We note that
![]() $X$
is not assumed to be in Fujiki’s class
$X$
is not assumed to be in Fujiki’s class
![]() ${\mathcal{C}}$
in Theorem 5.1. A key point of Theorem 5.1 is the assumption that
${\mathcal{C}}$
in Theorem 5.1. A key point of Theorem 5.1 is the assumption that
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Theorem 5.1. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a compact
$(X,\unicode[STIX]{x1D6E5})$
be a compact
![]() $\mathbb{Q}$
-factorial log surface. We assume that
$\mathbb{Q}$
-factorial log surface. We assume that
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Then we can construct a finite sequence of projective bimeromorphic morphisms
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Then we can construct a finite sequence of projective bimeromorphic morphisms
with
![]() $\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
,
$\unicode[STIX]{x1D6E5}_{i}:={\unicode[STIX]{x1D711}_{i-1}}_{\ast }\unicode[STIX]{x1D6E5}_{i-1}$
,
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
, and
$\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})=:C_{i}\simeq \mathbb{P}^{1}$
, and
![]() $-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
$-(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot C_{i}>0$
for every
![]() $i$
such that
$i$
such that
![]() $(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
$(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X^{\ast }$
. We note that
$X^{\ast }$
. We note that
![]() $(X_{i},\unicode[STIX]{x1D6E5}_{i})$
is a compact
$(X_{i},\unicode[STIX]{x1D6E5}_{i})$
is a compact
![]() $\mathbb{Q}$
-factorial log surface for every
$\mathbb{Q}$
-factorial log surface for every
![]() $i$
.
$i$
.
Proof. Since
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
, we can take an effective Cartier divisor
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
, we can take an effective Cartier divisor
![]() $D\in |m(K_{X}+\unicode[STIX]{x1D6E5})|$
for some large and divisible positive integer
$D\in |m(K_{X}+\unicode[STIX]{x1D6E5})|$
for some large and divisible positive integer
![]() $m$
. If
$m$
. If
![]() $m(K_{X}+\unicode[STIX]{x1D6E5})\cdot C=D\cdot C\geqslant 0$
for every curve
$m(K_{X}+\unicode[STIX]{x1D6E5})\cdot C=D\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
, then we set
$X$
, then we set
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast }):=(X_{0},\unicode[STIX]{x1D6E5}_{0})=(X,\unicode[STIX]{x1D6E5})$
. So we assume that there exists some irreducible curve
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast }):=(X_{0},\unicode[STIX]{x1D6E5}_{0})=(X,\unicode[STIX]{x1D6E5})$
. So we assume that there exists some irreducible curve
![]() $C$
on
$C$
on
![]() $X$
such that
$X$
such that
![]() $D\cdot C<0$
. Then
$D\cdot C<0$
. Then
![]() $C$
is an irreducible component of
$C$
is an irreducible component of
![]() $\operatorname{Supp}D$
and
$\operatorname{Supp}D$
and
![]() $C^{2}<0$
. By Sakai’s contraction theorem (see [Reference SakaiS, Theorem (1.2)]), which is a slight generalization of Grauert’s famous contraction theorem, we get a bimeromorphic morphism
$C^{2}<0$
. By Sakai’s contraction theorem (see [Reference SakaiS, Theorem (1.2)]), which is a slight generalization of Grauert’s famous contraction theorem, we get a bimeromorphic morphism
![]() $\unicode[STIX]{x1D711}_{0}:X=X_{0}\rightarrow X_{1}$
that contracts
$\unicode[STIX]{x1D711}_{0}:X=X_{0}\rightarrow X_{1}$
that contracts
![]() $C$
to a normal point of
$C$
to a normal point of
![]() $X_{1}$
. We take a divisible positive integer
$X_{1}$
. We take a divisible positive integer
![]() $l$
such that
$l$
such that
![]() $lC$
is Cartier. Then
$lC$
is Cartier. Then
![]() ${\mathcal{O}}_{X}(-lC)$
is a
${\mathcal{O}}_{X}(-lC)$
is a
![]() $\unicode[STIX]{x1D711}_{0}$
-ample line bundle on
$\unicode[STIX]{x1D711}_{0}$
-ample line bundle on
![]() $X$
. In particular,
$X$
. In particular,
![]() $\unicode[STIX]{x1D711}_{0}$
is a projective morphism. By construction,
$\unicode[STIX]{x1D711}_{0}$
is a projective morphism. By construction,
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
. Therefore,
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
. Therefore,
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})$
is
$-(K_{X}+\unicode[STIX]{x1D6E5})$
is
![]() $\unicode[STIX]{x1D711}_{0}$
-ample. Thus,
$\unicode[STIX]{x1D711}_{0}$
-ample. Thus,
![]() $R^{i}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{X}=0$
for every
$R^{i}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{X}=0$
for every
![]() $i>0$
by Theorem 11.3.
$i>0$
by Theorem 11.3.
Claim 1.
![]() $C$
is isomorphic to
$C$
is isomorphic to
![]() $\mathbb{P}^{1}$
.
$\mathbb{P}^{1}$
.
Proof of Claim 1.
We consider the following exact sequence:
where
![]() ${\mathcal{I}}_{C}$
is the defining ideal sheaf of
${\mathcal{I}}_{C}$
is the defining ideal sheaf of
![]() $C$
on
$C$
on
![]() $X$
. As we saw above,
$X$
. As we saw above,
![]() $R^{1}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{X}=0$
holds. Since
$R^{1}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{X}=0$
holds. Since
![]() $C$
is a curve,
$C$
is a curve,
![]() $R^{2}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{I}}_{C}=0$
holds by the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]). Thus we get
$R^{2}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{I}}_{C}=0$
holds by the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]). Thus we get
![]() $H^{1}(C,{\mathcal{O}}_{C})=R^{1}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{C}=0$
by the above exact sequence. This implies that
$H^{1}(C,{\mathcal{O}}_{C})=R^{1}{\unicode[STIX]{x1D711}_{0}}_{\ast }{\mathcal{O}}_{C}=0$
by the above exact sequence. This implies that
![]() $C$
is isomorphic to
$C$
is isomorphic to
![]() $\mathbb{P}^{1}$
.◻
$\mathbb{P}^{1}$
.◻
Therefore, by Theorem 3.11, we obtain that
![]() $(X_{1},\unicode[STIX]{x1D6E5}_{1})$
is a
$(X_{1},\unicode[STIX]{x1D6E5}_{1})$
is a
![]() $\mathbb{Q}$
-factorial log surface. Since
$\mathbb{Q}$
-factorial log surface. Since
![]() $\operatorname{Supp}D$
has only finitely many irreducible components, we get a desired sequence of contraction morphisms and finally obtain
$\operatorname{Supp}D$
has only finitely many irreducible components, we get a desired sequence of contraction morphisms and finally obtain
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
with
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
with
![]() $(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
$(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X^{\ast }$
.◻
$X^{\ast }$
.◻
We note the following well-known lemma on extremal rays of projective surfaces.
Lemma 5.2. Let
![]() $X$
be a normal projective surface, and let
$X$
be a normal projective surface, and let
![]() $C$
be a
$C$
be a
![]() $\mathbb{Q}$
-Cartier irreducible curve on
$\mathbb{Q}$
-Cartier irreducible curve on
![]() $X$
with
$X$
with
![]() $C^{2}<0$
. Then the numerical equivalence class
$C^{2}<0$
. Then the numerical equivalence class
![]() $[C]$
of
$[C]$
of
![]() $C$
spans an extremal ray of the Kleiman–Mori cone
$C$
spans an extremal ray of the Kleiman–Mori cone
![]() $\overline{\operatorname{NE}}(X)$
of
$\overline{\operatorname{NE}}(X)$
of
![]() $X$
.
$X$
.
Proof. This is obvious. For the proof, see [Reference Kollár and MoriKM, Lemma 1.22]. ◻
By Lemma 5.2, if
![]() $X$
is projective in Theorem 5.1, then the minimal model program in Theorem 5.1 is nothing but the minimal model program for projective
$X$
is projective in Theorem 5.1, then the minimal model program in Theorem 5.1 is nothing but the minimal model program for projective
![]() $\mathbb{Q}$
-factorial log surfaces formulated and established in [Reference FujinoFn4]. We also note that
$\mathbb{Q}$
-factorial log surfaces formulated and established in [Reference FujinoFn4]. We also note that
![]() $X$
is projective in Theorem 5.1 if the algebraic dimension
$X$
is projective in Theorem 5.1 if the algebraic dimension
![]() $a(X)$
of
$a(X)$
of
![]() $X$
is two by Lemma 4.1.
$X$
is two by Lemma 4.1.
We recall that
![]() $\mathbb{Q}$
-factorial log surfaces
$\mathbb{Q}$
-factorial log surfaces
![]() $(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
in Fujiki’s class
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
are projective by Lemma 4.3.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
are projective by Lemma 4.3.
Let us prove Theorem 1.1 except for the semiampleness of
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
.
Proof of Theorem 1.1.
If
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
, then we put
$X$
, then we put
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast }):=(X,\unicode[STIX]{x1D6E5})$
. We will see that
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast }):=(X,\unicode[STIX]{x1D6E5})$
. We will see that
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample in Theorem 7.2. We note that
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample in Theorem 7.2. We note that
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
. If
${\mathcal{C}}$
. If
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
, then
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
, then
![]() $X$
is projective by Lemma 4.3. Therefore, we can run the minimal model program for
$X$
is projective by Lemma 4.3. Therefore, we can run the minimal model program for
![]() $\mathbb{Q}$
-factorial projective log surfaces in [Reference FujinoFn4] and finally get a Mori fiber space. Therefore, we may further assume that
$\mathbb{Q}$
-factorial projective log surfaces in [Reference FujinoFn4] and finally get a Mori fiber space. Therefore, we may further assume that
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Then we can apply Theorem 5.1 and finally get a model
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Then we can apply Theorem 5.1 and finally get a model
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
such that
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
such that
![]() $(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
$(K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast })\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X^{\ast }$
. In this case, by the abundance theorem, Theorem 7.2, we will see that
$X^{\ast }$
. In this case, by the abundance theorem, Theorem 7.2, we will see that
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample.
Since we have
![]() $R^{1}{\unicode[STIX]{x1D711}_{i}}_{\ast }{\mathcal{O}}_{X_{i}}=0$
(see Theorem 11.3),
$R^{1}{\unicode[STIX]{x1D711}_{i}}_{\ast }{\mathcal{O}}_{X_{i}}=0$
(see Theorem 11.3),
![]() $X_{i}$
has only rational singularities if and only if so does
$X_{i}$
has only rational singularities if and only if so does
![]() $X_{i+1}$
by Lemma 2.8. Thus we have (2).
$X_{i+1}$
by Lemma 2.8. Thus we have (2).
Since each contraction
![]() $\unicode[STIX]{x1D711}_{i}$
is projective,
$\unicode[STIX]{x1D711}_{i}$
is projective,
![]() $X_{i}$
is projective when so is
$X_{i}$
is projective when so is
![]() $X_{i+1}$
. On the other hand, if
$X_{i+1}$
. On the other hand, if
![]() $X_{i}$
is projective, then so is
$X_{i}$
is projective, then so is
![]() $X_{i+1}$
because
$X_{i+1}$
because
![]() $\unicode[STIX]{x1D711}_{i}$
is nothing but the usual contraction morphism associated with a
$\unicode[STIX]{x1D711}_{i}$
is nothing but the usual contraction morphism associated with a
![]() $(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$
-negative extremal ray (see Lemma 5.2). Thus, we have (1).◻
$(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$
-negative extremal ray (see Lemma 5.2). Thus, we have (1).◻
We obtained Theorem 1.1 except for the semiampleness of
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
, which will be proved in Section 7.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
, which will be proved in Section 7.
6 Finite generation of log canonical rings
In this section, we briefly discuss the finite generation of log canonical rings of pairs for the reader’s convenience.
The following theorem is the main result of this section, which is essentially contained in [Reference FujinoFn4].
Theorem 6.1. (Finite generation of log canonical rings)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a compact
$(X,\unicode[STIX]{x1D6E5})$
be a compact
![]() $\mathbb{Q}$
-factorial log surface. Then the log canonical ring
$\mathbb{Q}$
-factorial log surface. Then the log canonical ring
is a finitely generated
![]() $\mathbb{C}$
-algebra. We note that the sheaf
$\mathbb{C}$
-algebra. We note that the sheaf
![]() ${\mathcal{O}}_{X}(\lfloor m(K_{X}+\unicode[STIX]{x1D6E5})\rfloor )$
denotes
${\mathcal{O}}_{X}(\lfloor m(K_{X}+\unicode[STIX]{x1D6E5})\rfloor )$
denotes
![]() $(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(\lfloor m\unicode[STIX]{x1D6E5}\rfloor ))^{\ast \ast }$
.
$(\unicode[STIX]{x1D714}_{X}^{\otimes m}\otimes {\mathcal{O}}_{X}(\lfloor m\unicode[STIX]{x1D6E5}\rfloor ))^{\ast \ast }$
.
As an easy consequence of Theorem 6.1, we have the following corollary.
Corollary 6.2. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a compact log canonical surface. Then the log canonical ring
$(X,\unicode[STIX]{x1D6E5})$
be a compact log canonical surface. Then the log canonical ring
is a finitely generated
![]() $\mathbb{C}$
-algebra.
$\mathbb{C}$
-algebra.
We note that
![]() $X$
is not assumed to be in Fujiki’s class
$X$
is not assumed to be in Fujiki’s class
![]() ${\mathcal{C}}$
in Theorem 6.1 and Corollary 6.2.
${\mathcal{C}}$
in Theorem 6.1 and Corollary 6.2.
Proof of Corollary 6.2.
Let
![]() $f:Y\rightarrow X$
be the minimal resolution. We put
$f:Y\rightarrow X$
be the minimal resolution. We put
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Since
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Since
![]() $(X,\unicode[STIX]{x1D6E5})$
is log canonical, we see that
$(X,\unicode[STIX]{x1D6E5})$
is log canonical, we see that
![]() $\unicode[STIX]{x1D6E5}_{Y}$
is a boundary
$\unicode[STIX]{x1D6E5}_{Y}$
is a boundary
![]() $\mathbb{Q}$
-divisor by the negativity lemma. By Theorem 6.1, the log canonical ring of
$\mathbb{Q}$
-divisor by the negativity lemma. By Theorem 6.1, the log canonical ring of
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is a finitely generated
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is a finitely generated
![]() $\mathbb{C}$
-algebra. This implies that the log canonical ring of
$\mathbb{C}$
-algebra. This implies that the log canonical ring of
![]() $(X,\unicode[STIX]{x1D6E5})$
is a finitely generated
$(X,\unicode[STIX]{x1D6E5})$
is a finitely generated
![]() $\mathbb{C}$
-algebra.◻
$\mathbb{C}$
-algebra.◻
Before we prove Theorem 6.1, let us recall the following easy well-known lemma for the reader’s convenience.
Lemma 6.3. Let
![]() $X$
be an irreducible compact normal analytic space and let
$X$
be an irreducible compact normal analytic space and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
such that
$X$
such that
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})\leqslant 1$
. Then the graded ring
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})\leqslant 1$
. Then the graded ring
is a finitely generated
![]() $\mathbb{C}$
-algebra.
$\mathbb{C}$
-algebra.
Sketch of Proof.
If
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})=-\infty$
or
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})=-\infty$
or
![]() $0$
, then it is very easy to see that
$0$
, then it is very easy to see that
![]() $R(X,{\mathcal{L}})$
is a finitely generated
$R(X,{\mathcal{L}})$
is a finitely generated
![]() $\mathbb{C}$
-algebra. If
$\mathbb{C}$
-algebra. If
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})=1$
, then we can reduce the problem to the case where
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})=1$
, then we can reduce the problem to the case where
![]() $X$
is a smooth projective curve and
$X$
is a smooth projective curve and
![]() ${\mathcal{L}}$
is an ample line bundle on
${\mathcal{L}}$
is an ample line bundle on
![]() $X$
by taking the Iitaka fibration (see [Reference MoriMo, (1.12) Theorem]). Thus,
$X$
by taking the Iitaka fibration (see [Reference MoriMo, (1.12) Theorem]). Thus,
![]() $R(X,{\mathcal{L}})$
is a finitely generated
$R(X,{\mathcal{L}})$
is a finitely generated
![]() $\mathbb{C}$
-algebra when
$\mathbb{C}$
-algebra when
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})\leqslant 1$
.◻
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})\leqslant 1$
.◻
Let us prove Theorem 6.1.
Proof of Theorem 6.1.
By Lemma 6.3, we may assume that
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
. Then, by Corollary 4.2,
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
. Then, by Corollary 4.2,
![]() $X$
is projective. In this case, the log canonical ring
$X$
is projective. In this case, the log canonical ring
of
![]() $(X,\unicode[STIX]{x1D6E5})$
is a finitely generated
$(X,\unicode[STIX]{x1D6E5})$
is a finitely generated
![]() $\mathbb{C}$
-algebra by the minimal model theory for projective
$\mathbb{C}$
-algebra by the minimal model theory for projective
![]() $\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4].◻
$\mathbb{Q}$
-factorial log surfaces established in [Reference FujinoFn4].◻
Let us quickly see some results and conjectures on log canonical rings of higher-dimensional pairs.
Theorem 6.4. ([Reference Birkar, Cascini, Hacon and McKernanBCHM], [Reference Fujino and MoriFM], and [Reference FujinoFn5, Theorem 1.8])
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a Kawamata log terminal pair such that
$(X,\unicode[STIX]{x1D6E5})$
be a Kawamata log terminal pair such that
![]() $\unicode[STIX]{x1D6E5}$
is a
$\unicode[STIX]{x1D6E5}$
is a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
and that
$X$
and that
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
. Then the log canonical ring
${\mathcal{C}}$
. Then the log canonical ring
is a finitely generated
![]() $\mathbb{C}$
-algebra.
$\mathbb{C}$
-algebra.
Conjecture 6.5. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical pair such that
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical pair such that
![]() $\unicode[STIX]{x1D6E5}$
is a
$\unicode[STIX]{x1D6E5}$
is a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
and that
$X$
and that
![]() $X$
is in Fujiki’s class
$X$
is in Fujiki’s class
![]() ${\mathcal{C}}$
. Then the log canonical ring
${\mathcal{C}}$
. Then the log canonical ring
is a finitely generated
![]() $\mathbb{C}$
-algebra.
$\mathbb{C}$
-algebra.
Conjecture 6.5 is still widely open even when
![]() $X$
is projective (see [Reference FujinoFn2], [Reference FujinoFn5], [Reference Fujino and GongyoFG], [Reference HashizumeHa2], and [Reference Fujino and LiuFL]). When
$X$
is projective (see [Reference FujinoFn2], [Reference FujinoFn5], [Reference Fujino and GongyoFG], [Reference HashizumeHa2], and [Reference Fujino and LiuFL]). When
![]() $X$
is projective in Conjecture 6.5, it is essentially equivalent to the existence problem of good minimal models for lower-dimensional varieties (for the details, see [Reference Fujino and GongyoFG]). Note that Corollary 6.2 completely settled Conjecture 6.5 in dimension two.
$X$
is projective in Conjecture 6.5, it is essentially equivalent to the existence problem of good minimal models for lower-dimensional varieties (for the details, see [Reference Fujino and GongyoFG]). Note that Corollary 6.2 completely settled Conjecture 6.5 in dimension two.
We close this section with a naive question.
Question 6.6. Let
![]() $X$
be an irreducible compact normal analytic surface such that
$X$
be an irreducible compact normal analytic surface such that
![]() $K_{X}$
is
$K_{X}$
is
![]() $\mathbb{Q}$
-Cartier. Then, is the canonical ring
$\mathbb{Q}$
-Cartier. Then, is the canonical ring
a finitely generated
![]() $\mathbb{C}$
-algebra?
$\mathbb{C}$
-algebra?
We do not know the answer even when
![]() $X$
is projective.
$X$
is projective.
7 Abundance theorem
In this section, we prove the abundance theorem for
![]() $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Let us start with the nonvanishing theorem.
Theorem 7.1. (Nonvanishing theorem)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a
$(X,\unicode[STIX]{x1D6E5})$
be a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. Then we have
$X$
. Then we have
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.
Proof. Let
![]() $f:Y\rightarrow X$
be the minimal resolution. We put
$f:Y\rightarrow X$
be the minimal resolution. We put
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
![]() $\unicode[STIX]{x1D6E5}_{Y}$
is an effective
$\unicode[STIX]{x1D6E5}_{Y}$
is an effective
![]() $\mathbb{Q}$
-divisor by the negativity lemma. If
$\mathbb{Q}$
-divisor by the negativity lemma. If
![]() $\unicode[STIX]{x1D705}(Y,K_{Y})\geqslant 0$
, then we have
$\unicode[STIX]{x1D705}(Y,K_{Y})\geqslant 0$
, then we have
Therefore, from now on, we assume that
![]() $\unicode[STIX]{x1D705}(Y,K_{Y})=-\infty$
. By Lemma 4.3,
$\unicode[STIX]{x1D705}(Y,K_{Y})=-\infty$
. By Lemma 4.3,
![]() $Y$
is projective. Therefore, by Lemma 4.1,
$Y$
is projective. Therefore, by Lemma 4.1,
![]() $X$
is projective since
$X$
is projective since
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial by assumption. Thus, by [Reference FujinoFn4, Theorem 5.1], we get
$\mathbb{Q}$
-factorial by assumption. Thus, by [Reference FujinoFn4, Theorem 5.1], we get
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.◻
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.◻
The following theorem is the main result of this section, which is the abundance theorem for
![]() $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Theorem 7.2. (Abundance theorem for
 $\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
$\mathbb{Q}$
-factorial log surfaces in Fujiki’s class
 ${\mathcal{C}}$
)
${\mathcal{C}}$
)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a
$(X,\unicode[STIX]{x1D6E5})$
be a
![]() $\mathbb{Q}$
-factorial log surface in Fujiki’s class
$\mathbb{Q}$
-factorial log surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. Then
$X$
. Then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
For the proof of Theorem 7.2, we prepare some easy lemmas.
Lemma 7.3. Let
![]() $X$
be a compact normal analytic surface, and let
$X$
be a compact normal analytic surface, and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
such that
$X$
such that
![]() ${\mathcal{L}}\cdot C\geqslant 0$
for every curve
${\mathcal{L}}\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. Assume that
$X$
. Assume that
![]() $\unicode[STIX]{x1D705}(X,{\mathcal{L}})=1$
. Then
$\unicode[STIX]{x1D705}(X,{\mathcal{L}})=1$
. Then
![]() ${\mathcal{L}}$
is semiample.
${\mathcal{L}}$
is semiample.
Proof. This is an easy consequence of Zariski’s lemma (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter III, (8.2) Lemma]). For the details, see [Reference FujitaFt, (4.1) Theorem]. ◻
Lemma 7.4. Let
![]() $S$
be a compact smooth analytic surface in Fujiki’s class
$S$
be a compact smooth analytic surface in Fujiki’s class
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}(S,K_{S})=0$
. Assume that the algebraic dimension
$\unicode[STIX]{x1D705}(S,K_{S})=0$
. Assume that the algebraic dimension
![]() $a(S)$
of
$a(S)$
of
![]() $S$
is less than two. Then
$S$
is less than two. Then
![]() $S$
is bimeromorphically equivalent to a
$S$
is bimeromorphically equivalent to a
![]() $K3$
surface or a two-dimensional complex torus.
$K3$
surface or a two-dimensional complex torus.
Proof. Since
![]() $S$
is in Fujiki’s class
$S$
is in Fujiki’s class
![]() ${\mathcal{C}}$
, the first Betti number
${\mathcal{C}}$
, the first Betti number
![]() $b_{1}(S)$
of
$b_{1}(S)$
of
![]() $S$
is even. Then the Enriques–Kodaira classification (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]) and
$S$
is even. Then the Enriques–Kodaira classification (see [Reference Barth, Hulek, Peters and de VenBHPV, Chapter VI]) and
![]() $\unicode[STIX]{x1D705}(S,K_{S})=0$
give the desired statement.◻
$\unicode[STIX]{x1D705}(S,K_{S})=0$
give the desired statement.◻
Lemma 7.5. Let
![]() $B$
be a nonzero effective divisor on a two-dimensional complex torus
$B$
be a nonzero effective divisor on a two-dimensional complex torus
![]() $S$
. Then we have
$S$
. Then we have
![]() $\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.
$\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.
Proof. Without loss of generality, we may assume that
![]() $B$
is an irreducible curve on
$B$
is an irreducible curve on
![]() $S$
. If
$S$
. If
![]() $B$
is not an elliptic curve, then we can see that
$B$
is not an elliptic curve, then we can see that
![]() $S$
is an Abelian surface (see [Reference UenoU, Lemma 10.8]). In this case, it is well known that
$S$
is an Abelian surface (see [Reference UenoU, Lemma 10.8]). In this case, it is well known that
![]() $|2B|$
is basepoint-free. In particular,
$|2B|$
is basepoint-free. In particular,
![]() $\unicode[STIX]{x1D705}(S,B)\geqslant 1$
. Therefore, from now on, we assume that
$\unicode[STIX]{x1D705}(S,B)\geqslant 1$
. Therefore, from now on, we assume that
![]() $B$
is an elliptic curve. By taking a suitable translation, we may further assume that
$B$
is an elliptic curve. By taking a suitable translation, we may further assume that
![]() $B$
is a complex subtorus of
$B$
is a complex subtorus of
![]() $S$
. We set
$S$
. We set
![]() $A=S/B$
. Let
$A=S/B$
. Let
![]() $p:S\rightarrow A$
be the canonical quotient map. Then
$p:S\rightarrow A$
be the canonical quotient map. Then
![]() $B=p^{\ast }P$
holds for
$B=p^{\ast }P$
holds for
![]() $P=p(B)\in A$
. Therefore, we obtain
$P=p(B)\in A$
. Therefore, we obtain
![]() $\unicode[STIX]{x1D705}(S,B)=\unicode[STIX]{x1D705}(A,P)=1$
. Hence, we always have
$\unicode[STIX]{x1D705}(S,B)=\unicode[STIX]{x1D705}(A,P)=1$
. Hence, we always have
![]() $\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.◻
$\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.◻
Lemma 7.6. Let
![]() $S$
be a
$S$
be a
![]() $K3$
surface, and let
$K3$
surface, and let
![]() $B$
be a nonzero effective divisor on
$B$
be a nonzero effective divisor on
![]() $S$
such that
$S$
such that
![]() $B^{2}=0$
. Then we have
$B^{2}=0$
. Then we have
![]() $\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.
$\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.
Proof. By the Riemann–Roch formula,
By Serre duality,
Since
![]() $B$
is a nonzero effective divisor on
$B$
is a nonzero effective divisor on
![]() $S$
,
$S$
,
![]() $H^{0}(S,{\mathcal{O}}_{S}(-B))=0$
and
$H^{0}(S,{\mathcal{O}}_{S}(-B))=0$
and
![]() $\dim H^{0}(S,{\mathcal{O}}_{S}(B))\geqslant 2$
. Therefore, we have
$\dim H^{0}(S,{\mathcal{O}}_{S}(B))\geqslant 2$
. Therefore, we have
![]() $\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.◻
$\unicode[STIX]{x1D705}(S,B)\geqslant 1$
.◻
Before we prove Theorem 7.2, we explicitly state the abundance theorem for log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Corollary 7.7. (Abundance theorem for log canonical surfaces in Fujiki’s class
 ${\mathcal{C}}$
)
${\mathcal{C}}$
)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
. Then
$X$
. Then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
Proof. Let
![]() $f:Y\rightarrow X$
be the minimal resolution of
$f:Y\rightarrow X$
be the minimal resolution of
![]() $X$
. We put
$X$
. We put
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
![]() $\unicode[STIX]{x1D6E5}_{Y}$
is effective by the negativity lemma and is a subboundary
$\unicode[STIX]{x1D6E5}_{Y}$
is effective by the negativity lemma and is a subboundary
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $Y$
since
$Y$
since
![]() $(X,\unicode[STIX]{x1D6E5})$
is log canonical. Therefore,
$(X,\unicode[STIX]{x1D6E5})$
is log canonical. Therefore,
![]() $\unicode[STIX]{x1D6E5}_{Y}$
is a boundary
$\unicode[STIX]{x1D6E5}_{Y}$
is a boundary
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $Y$
. We can easily see that
$Y$
. We can easily see that
![]() $(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}\geqslant 0$
for every curve
$(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}\geqslant 0$
for every curve
![]() $C_{Y}$
on
$C_{Y}$
on
![]() $Y$
. Thus, by Theorem 7.2,
$Y$
. Thus, by Theorem 7.2,
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is semiample. This implies that
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is semiample. This implies that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is also semiample.◻
$K_{X}+\unicode[STIX]{x1D6E5}$
is also semiample.◻
Let us start the proof of Theorem 7.2.
Proof of Theorem 7.2.
By the nonvanishing theorem (see Theorem 7.1), we have
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
.
Step 1. (
 $\unicode[STIX]{x1D705}=2$
)
$\unicode[STIX]{x1D705}=2$
)
If
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
, then
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=2$
, then
![]() $X$
is projective by Corollary 4.2. In this case, we can apply [Reference FujinoFn4, Theorem 4.1], which is one of the deepest results in [Reference FujinoFn4], and obtain that
$X$
is projective by Corollary 4.2. In this case, we can apply [Reference FujinoFn4, Theorem 4.1], which is one of the deepest results in [Reference FujinoFn4], and obtain that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample.
Step 2. (
 $\unicode[STIX]{x1D705}=1$
)
$\unicode[STIX]{x1D705}=1$
)
If
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=1$
, then we see that
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=1$
, then we see that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by Lemma 7.3.
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by Lemma 7.3.
Step 3. (
 $\unicode[STIX]{x1D705}=0$
)
$\unicode[STIX]{x1D705}=0$
)
In this step, we assume
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=0$
. If
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=0$
. If
![]() $X$
is projective, then
$X$
is projective, then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by [Reference FujinoFn4, Theorem 6.2]. Here, we will explain that the proof of [Reference FujinoFn4, Theorem 6.2] works with some minor modifications when
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by [Reference FujinoFn4, Theorem 6.2]. Here, we will explain that the proof of [Reference FujinoFn4, Theorem 6.2] works with some minor modifications when
![]() $X$
is not projective. From now on, we will freely use the notation of the proof of [Reference FujinoFn4, Theorem 6.2].
$X$
is not projective. From now on, we will freely use the notation of the proof of [Reference FujinoFn4, Theorem 6.2].
The first part of the proof of [Reference FujinoFn4, Theorem 6.2] works without any changes (see page 361 in [Reference FujinoFn4]). We note that
![]() $Z$
is a member of
$Z$
is a member of
![]() $|m(K_{S}+\unicode[STIX]{x1D6E5}_{S})|$
for some divisible positive integer
$|m(K_{S}+\unicode[STIX]{x1D6E5}_{S})|$
for some divisible positive integer
![]() $m$
. We also note that Mumford’s arguments on indecomposable curves of canonical type work on smooth analytic surfaces (see [Reference MumfordMu2, Definition, Lemma, and Corollary 1 in Section 2]). Therefore, [Reference FujinoFn4, Lemma 6.3] holds true. In particular, we obtain that
$m$
. We also note that Mumford’s arguments on indecomposable curves of canonical type work on smooth analytic surfaces (see [Reference MumfordMu2, Definition, Lemma, and Corollary 1 in Section 2]). Therefore, [Reference FujinoFn4, Lemma 6.3] holds true. In particular, we obtain that
![]() $Z^{2}=0$
. The compact smooth surface
$Z^{2}=0$
. The compact smooth surface
![]() $S$
constructed in the first part of [Reference FujinoFn4, Theorem 6.2] is not projective. Of course,
$S$
constructed in the first part of [Reference FujinoFn4, Theorem 6.2] is not projective. Of course,
![]() $S$
is in Fujiki’s class
$S$
is in Fujiki’s class
![]() ${\mathcal{C}}$
because
${\mathcal{C}}$
because
![]() $S$
is bimeromorphically equivalent to
$S$
is bimeromorphically equivalent to
![]() $X$
by construction. As in the proof of [Reference FujinoFn4, Theorem 6.2], we will derive a contradiction assuming
$X$
by construction. As in the proof of [Reference FujinoFn4, Theorem 6.2], we will derive a contradiction assuming
![]() $Z\neq 0$
.
$Z\neq 0$
.
By Lemma 4.3, we have
![]() $\unicode[STIX]{x1D705}(S,K_{S})\geqslant 0$
since
$\unicode[STIX]{x1D705}(S,K_{S})\geqslant 0$
since
![]() $S$
is not projective. Thus, all we have to do is to check that Step 1 in the proof of [Reference FujinoFn4, Theorem 6.2] works when
$S$
is not projective. Thus, all we have to do is to check that Step 1 in the proof of [Reference FujinoFn4, Theorem 6.2] works when
![]() $S$
is not projective.
$S$
is not projective.
In Step 1 in the proof of [Reference FujinoFn4, Theorem 6.2],
![]() $S$
is a compact smooth analytic surface with
$S$
is a compact smooth analytic surface with
![]() $\unicode[STIX]{x1D705}(S,K_{S})=0$
and there are no
$\unicode[STIX]{x1D705}(S,K_{S})=0$
and there are no
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $S$
. Since
$S$
. Since
![]() $S$
is in Fujiki’s class
$S$
is in Fujiki’s class
![]() ${\mathcal{C}}$
, the first Betti number
${\mathcal{C}}$
, the first Betti number
![]() $b_{1}(S)$
of
$b_{1}(S)$
of
![]() $S$
is even. Therefore, by the Enriques–Kodaira classification,
$S$
is even. Therefore, by the Enriques–Kodaira classification,
![]() $S$
is a
$S$
is a
![]() $K3$
surface or a complex torus (see Lemma 7.4). Then, by Lemmas 7.5 and 7.6, we have
$K3$
surface or a complex torus (see Lemma 7.4). Then, by Lemmas 7.5 and 7.6, we have
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D705}(S,K_{S}+\unicode[STIX]{x1D6E5}_{S})=\unicode[STIX]{x1D705}(S,Z)\geqslant 1$
and get a contradiction. This means that Step 1 in the proof of [Reference FujinoFn4, Theorem 6.2] works when
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D705}(S,K_{S}+\unicode[STIX]{x1D6E5}_{S})=\unicode[STIX]{x1D705}(S,Z)\geqslant 1$
and get a contradiction. This means that Step 1 in the proof of [Reference FujinoFn4, Theorem 6.2] works when
![]() $S$
is not projective.
$S$
is not projective.
Therefore,
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is always semiample. This is what we wanted.◻
$K_{X}+\unicode[STIX]{x1D6E5}$
is always semiample. This is what we wanted.◻
8 Contraction theorem for log canonical surfaces
In this section, we discuss a contraction theorem for log canonical surfaces. Note that compact log canonical surfaces are not necessarily
![]() $\mathbb{Q}$
-factorial. Therefore, we need Mumford’s intersection theory (see [Reference MumfordMu1], [Reference MatsukiMa, Remark 4-6-3], and [Reference SakaiS]).
$\mathbb{Q}$
-factorial. Therefore, we need Mumford’s intersection theory (see [Reference MumfordMu1], [Reference MatsukiMa, Remark 4-6-3], and [Reference SakaiS]).
Definition 8.1. (Mumford’s intersection theory)
Let
![]() $X$
be a normal analytic surface, and let
$X$
be a normal analytic surface, and let
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a resolution. Let
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a resolution. Let
![]() $\operatorname{Exc}(\unicode[STIX]{x1D70B})=\sum _{i}E_{i}$
be the irreducible decomposition of the exceptional curve of
$\operatorname{Exc}(\unicode[STIX]{x1D70B})=\sum _{i}E_{i}$
be the irreducible decomposition of the exceptional curve of
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Then we can define the inverse image
$X$
. Then we can define the inverse image
![]() $\unicode[STIX]{x1D70B}^{\ast }D$
as
$\unicode[STIX]{x1D70B}^{\ast }D$
as
where
![]() $D^{\dagger }$
is the strict transform of
$D^{\dagger }$
is the strict transform of
![]() $D$
by
$D$
by
![]() $\unicode[STIX]{x1D70B}$
and the rational numbers
$\unicode[STIX]{x1D70B}$
and the rational numbers
![]() $\unicode[STIX]{x1D6FC}_{i}$
are uniquely determined by the following linear equations:
$\unicode[STIX]{x1D6FC}_{i}$
are uniquely determined by the following linear equations:
for every
![]() $j$
. We call
$j$
. We call
![]() $\unicode[STIX]{x1D70B}^{\ast }D$
the pull-back of
$\unicode[STIX]{x1D70B}^{\ast }D$
the pull-back of
![]() $D$
in the sense of Mumford. Of course,
$D$
in the sense of Mumford. Of course,
![]() $\unicode[STIX]{x1D70B}^{\ast }D$
coincides with the usual one when
$\unicode[STIX]{x1D70B}^{\ast }D$
coincides with the usual one when
![]() $D$
is
$D$
is
![]() $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.
From now on, we further assume that
![]() $X$
is compact. The intersection number
$X$
is compact. The intersection number
![]() $D\cdot D^{\prime }$
(in the sense of Mumford) is defined to be the rational number
$D\cdot D^{\prime }$
(in the sense of Mumford) is defined to be the rational number
![]() $(\unicode[STIX]{x1D70B}^{\ast }D)\cdot (\unicode[STIX]{x1D70B}^{\ast }D^{\prime })$
, where
$(\unicode[STIX]{x1D70B}^{\ast }D)\cdot (\unicode[STIX]{x1D70B}^{\ast }D^{\prime })$
, where
![]() $D$
and
$D$
and
![]() $D^{\prime }$
are
$D^{\prime }$
are
![]() $\mathbb{Q}$
-divisors on
$\mathbb{Q}$
-divisors on
![]() $X$
. We can easily see that
$X$
. We can easily see that
![]() $D\cdot D^{\prime }$
is well defined. We note that it coincides with the usual one when
$D\cdot D^{\prime }$
is well defined. We note that it coincides with the usual one when
![]() $D$
or
$D$
or
![]() $D^{\prime }$
is
$D^{\prime }$
is
![]() $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.
Let us recall some definitions and basic properties of surface singularities for the reader’s convenience.
Definition 8.2. (Numerically log canonical and numerically dlt; see [Reference Kollár and MoriKM, Notation 4.1])
Let
![]() $X$
be a normal analytic surface, and let
$X$
be a normal analytic surface, and let
![]() $\unicode[STIX]{x1D6E5}$
be a
$\unicode[STIX]{x1D6E5}$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Let
$X$
. Let
![]() $f:Y\rightarrow U\subset X$
be a proper bimeromorphic morphism from a smooth surface
$f:Y\rightarrow U\subset X$
be a proper bimeromorphic morphism from a smooth surface
![]() $Y$
to an open set
$Y$
to an open set
![]() $U$
of
$U$
of
![]() $X$
. Then we can define
$X$
. Then we can define
![]() $f^{\ast }(K_{U}+\unicode[STIX]{x1D6E5}|_{U})$
in the sense of Mumford (see Definition 8.1) without assuming that
$f^{\ast }(K_{U}+\unicode[STIX]{x1D6E5}|_{U})$
in the sense of Mumford (see Definition 8.1) without assuming that
![]() $K_{U}+\unicode[STIX]{x1D6E5}|_{U}$
is
$K_{U}+\unicode[STIX]{x1D6E5}|_{U}$
is
![]() $\mathbb{Q}$
-Cartier. Thus we can always write
$\mathbb{Q}$
-Cartier. Thus we can always write
such that
![]() $f_{\ast }(\sum _{E_{i}}a(E_{i},X,\unicode[STIX]{x1D6E5})E_{i})=-\unicode[STIX]{x1D6E5}|_{U}$
. If
$f_{\ast }(\sum _{E_{i}}a(E_{i},X,\unicode[STIX]{x1D6E5})E_{i})=-\unicode[STIX]{x1D6E5}|_{U}$
. If
![]() $\unicode[STIX]{x1D6E5}$
is effective and
$\unicode[STIX]{x1D6E5}$
is effective and
![]() $a(E_{i},X,\unicode[STIX]{x1D6E5})\geqslant -1$
for every exceptional curve
$a(E_{i},X,\unicode[STIX]{x1D6E5})\geqslant -1$
for every exceptional curve
![]() $E_{i}$
and
$E_{i}$
and
![]() $f:Y\rightarrow U\subset X$
, then we say that
$f:Y\rightarrow U\subset X$
, then we say that
![]() $(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical. We say that
$(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical. We say that
![]() $(X,\unicode[STIX]{x1D6E5})$
is numerically dlt if
$(X,\unicode[STIX]{x1D6E5})$
is numerically dlt if
![]() $(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical and there exists a finite set
$(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical and there exists a finite set
![]() $Z\subset X$
such that
$Z\subset X$
such that
![]() $X\setminus Z$
is smooth,
$X\setminus Z$
is smooth,
![]() $\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
is a simple normal crossing divisor on
$\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
is a simple normal crossing divisor on
![]() $X\setminus Z$
, and
$X\setminus Z$
, and
![]() $a(E,X,\unicode[STIX]{x1D6E5})>-1$
for every exceptional curve
$a(E,X,\unicode[STIX]{x1D6E5})>-1$
for every exceptional curve
![]() $E$
which maps to
$E$
which maps to
![]() $Z$
. It is well known that if
$Z$
. It is well known that if
![]() $(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical, then
$(X,\unicode[STIX]{x1D6E5})$
is numerically log canonical, then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier (see [Reference FujinoFn4, Proposition 3.5] and [Reference MatsukiMa, Remark 4-6-3]). Moreover, if
$\mathbb{Q}$
-Cartier (see [Reference FujinoFn4, Proposition 3.5] and [Reference MatsukiMa, Remark 4-6-3]). Moreover, if
![]() $(X,\unicode[STIX]{x1D6E5})$
is numerically dlt, then
$(X,\unicode[STIX]{x1D6E5})$
is numerically dlt, then
![]() $X$
has only rational singularities (see [Reference Kollár and MoriKM, Theorem 4.12]).
$X$
has only rational singularities (see [Reference Kollár and MoriKM, Theorem 4.12]).
Remark 8.3. In Definition 8.2, we only require that
![]() $\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
is a simple normal crossing divisor on
$\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
is a simple normal crossing divisor on
![]() $X\setminus Z$
in the classical topology. So it permits some irreducible component of
$X\setminus Z$
in the classical topology. So it permits some irreducible component of
![]() $\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
to have nodal singularities. Therefore, our definition does not coincide with [Reference Kollár and MoriKM, Notation 4.1] when
$\operatorname{Supp}\unicode[STIX]{x1D6E5}|_{X\setminus Z}$
to have nodal singularities. Therefore, our definition does not coincide with [Reference Kollár and MoriKM, Notation 4.1] when
![]() $X$
is an algebraic surface. However, since we are mainly interested in local analytic properties of singularities of pairs
$X$
is an algebraic surface. However, since we are mainly interested in local analytic properties of singularities of pairs
![]() $(X,\unicode[STIX]{x1D6E5})$
, this difference causes no subtle problems.
$(X,\unicode[STIX]{x1D6E5})$
, this difference causes no subtle problems.
We need the following contraction theorem for log canonical surfaces in Sections 9 and 10.
Theorem 8.4. (Contraction theorem for log canonical surfaces; see [Reference FujinoFn6, Theorem 4.1])
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a compact log canonical surface, and let
$(X,\unicode[STIX]{x1D6E5})$
be a compact log canonical surface, and let
![]() $C$
be an irreducible curve on
$C$
be an irreducible curve on
![]() $X$
such that
$X$
such that
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
and
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
and
![]() $C^{2}<0$
, where
$C^{2}<0$
, where
![]() $C^{2}$
is the self-intersection number of
$C^{2}$
is the self-intersection number of
![]() $C$
in the sense of Mumford (see Definition 8.1). Then we have a projective bimeromorphic morphism
$C$
in the sense of Mumford (see Definition 8.1). Then we have a projective bimeromorphic morphism
![]() $\unicode[STIX]{x1D711}:X\rightarrow Y$
onto a normal surface
$\unicode[STIX]{x1D711}:X\rightarrow Y$
onto a normal surface
![]() $Y$
such that
$Y$
such that
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711})=C\simeq \mathbb{P}^{1}$
and that
$\operatorname{Exc}(\unicode[STIX]{x1D711})=C\simeq \mathbb{P}^{1}$
and that
![]() $C$
passes through no nonrational singular points of
$C$
passes through no nonrational singular points of
![]() $X$
, that is,
$X$
, that is,
![]() $X$
has only rational singularities in a neighborhood of
$X$
has only rational singularities in a neighborhood of
![]() $C$
. In particular,
$C$
. In particular,
![]() $C$
is
$C$
is
![]() $\mathbb{Q}$
-Cartier. Moreover,
$\mathbb{Q}$
-Cartier. Moreover,
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is log canonical with
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is log canonical with
![]() $\unicode[STIX]{x1D6E5}_{Y}:=\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}_{Y}:=\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6E5}$
.
Proof. By Sakai’s contraction theorem (see [Reference SakaiS, Theorem (1.2)]), we have a bimeromorphic morphism
![]() $\unicode[STIX]{x1D711}:X\rightarrow Y$
, which contracts
$\unicode[STIX]{x1D711}:X\rightarrow Y$
, which contracts
![]() $C$
to a normal point
$C$
to a normal point
![]() $P\in Y$
. Since
$P\in Y$
. Since
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
,
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
,
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is numerically dlt in a neighborhood of
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is numerically dlt in a neighborhood of
![]() $P$
by the negativity lemma. Therefore,
$P$
by the negativity lemma. Therefore,
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is
![]() $\mathbb{Q}$
-Cartier and
$\mathbb{Q}$
-Cartier and
![]() $Y$
has only rational singularities in a neighborhood of
$Y$
has only rational singularities in a neighborhood of
![]() $P$
. Of course,
$P$
. Of course,
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is a compact log canonical surface. By Theorem 11.3,
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is a compact log canonical surface. By Theorem 11.3,
![]() $R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
for every
$R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
for every
![]() $i>0$
. Thus,
$i>0$
. Thus,
![]() $X$
has only rational singularities in a neighborhood of
$X$
has only rational singularities in a neighborhood of
![]() $C$
by Lemma 2.8. In particular,
$C$
by Lemma 2.8. In particular,
![]() $C$
is
$C$
is
![]() $\mathbb{Q}$
-Cartier (see [Reference NakayamaNk, Chapter II, 2.12. Lemma]). Since
$\mathbb{Q}$
-Cartier (see [Reference NakayamaNk, Chapter II, 2.12. Lemma]). Since
![]() $R^{1}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
, we can easily check that
$R^{1}\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{X}=0$
, we can easily check that
![]() $C\simeq \mathbb{P}^{1}$
as in Claim 1 of the proof of Theorem 5.1. We see that
$C\simeq \mathbb{P}^{1}$
as in Claim 1 of the proof of Theorem 5.1. We see that
![]() $\unicode[STIX]{x1D711}$
is projective;
$\unicode[STIX]{x1D711}$
is projective;
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})$
and
$-(K_{X}+\unicode[STIX]{x1D6E5})$
and
![]() $-C$
are
$-C$
are
![]() $\unicode[STIX]{x1D711}$
-ample by construction.◻
$\unicode[STIX]{x1D711}$
-ample by construction.◻
We close this section with simple but very important remarks.
Remark 8.5. (Extremal rays)
Theorem 8.4 says that
![]() $X$
has only rational singularities in a neighborhood of the exceptional curve
$X$
has only rational singularities in a neighborhood of the exceptional curve
![]() $C$
and then
$C$
and then
![]() $C$
is automatically
$C$
is automatically
![]() $\mathbb{Q}$
-Cartier. Therefore, if
$\mathbb{Q}$
-Cartier. Therefore, if
![]() $X$
is projective, then
$X$
is projective, then
![]() $C$
spans a
$C$
spans a
![]() $(K_{X}+\unicode[STIX]{x1D6E5})$
-negative extremal ray
$(K_{X}+\unicode[STIX]{x1D6E5})$
-negative extremal ray
![]() $R$
of
$R$
of
![]() $\overline{\operatorname{NE}}(X)$
in the usual sense (see Lemma 5.2). Thus the contraction
$\overline{\operatorname{NE}}(X)$
in the usual sense (see Lemma 5.2). Thus the contraction
![]() $\unicode[STIX]{x1D711}$
in Theorem 8.4 is nothing but the usual contraction morphism associated with the extremal ray
$\unicode[STIX]{x1D711}$
in Theorem 8.4 is nothing but the usual contraction morphism associated with the extremal ray
![]() $R$
. In particular,
$R$
. In particular,
![]() $Y$
is also projective when so is
$Y$
is also projective when so is
![]() $X$
.
$X$
.
Remark 8.6. (Termination of contractions)
Assume that
![]() $X$
is Moishezon. We consider a sequence of contraction morphisms as in Theorem 8.4,
$X$
is Moishezon. We consider a sequence of contraction morphisms as in Theorem 8.4,
starting from a log canonical surface
![]() $(X_{0},\unicode[STIX]{x1D6E5}_{0}):=(X,\unicode[STIX]{x1D6E5})$
. Let
$(X_{0},\unicode[STIX]{x1D6E5}_{0}):=(X,\unicode[STIX]{x1D6E5})$
. Let
![]() $C_{i}$
be the
$C_{i}$
be the
![]() $\unicode[STIX]{x1D711}_{i}$
-exceptional curve for every
$\unicode[STIX]{x1D711}_{i}$
-exceptional curve for every
![]() $i$
. By Theorem 8.4,
$i$
. By Theorem 8.4,
![]() $C_{i}$
is
$C_{i}$
is
![]() $\mathbb{Q}$
-Cartier for every
$\mathbb{Q}$
-Cartier for every
![]() $i$
. Then we can easily see that
$i$
. Then we can easily see that
![]() $C_{0}$
,
$C_{0}$
,
![]() $\unicode[STIX]{x1D711}_{0}^{\ast }C_{1}$
,
$\unicode[STIX]{x1D711}_{0}^{\ast }C_{1}$
,
![]() $\ldots$
,
$\ldots$
,
![]() $\unicode[STIX]{x1D711}_{0}^{\ast }\cdots \unicode[STIX]{x1D711}_{i-1}^{\ast }C_{i}$
,
$\unicode[STIX]{x1D711}_{0}^{\ast }\cdots \unicode[STIX]{x1D711}_{i-1}^{\ast }C_{i}$
,
![]() $\ldots$
are linearly independent in
$\ldots$
are linearly independent in
![]() $N^{1}(X)$
. Therefore, the sequence must terminate since
$N^{1}(X)$
. Therefore, the sequence must terminate since
![]() $\unicode[STIX]{x1D70C}(X)<\infty$
.
$\unicode[STIX]{x1D70C}(X)<\infty$
.
9 Log canonical surfaces in Fujiki’s class
 ${\mathcal{C}}$
with negative Kodaira dimension
${\mathcal{C}}$
with negative Kodaira dimension
The main purpose of this section is to prove the following theorem.
Theorem 9.1. (see Theorem 1.3)
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
. Assume that
${\mathcal{C}}$
. Assume that
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Then
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
holds. Then
![]() $X$
is projective.
$X$
is projective.
Let us recall the following well-known lemma for the reader’s convenience (see [Reference MatsukiMa, Remark 4-6-29]).
Lemma 9.2. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface. Assume that
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface. Assume that
![]() $P\in X$
is not a rational singularity. Then
$P\in X$
is not a rational singularity. Then
![]() $P\not \in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
and
$P\not \in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
and
![]() $X$
is Gorenstein at
$X$
is Gorenstein at
![]() $P$
.
$P$
.
Sketch of Proof.
If
![]() $P\in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
, then
$P\in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
, then
![]() $(X,0)$
is numerically dlt in a neighborhood of
$(X,0)$
is numerically dlt in a neighborhood of
![]() $P$
. In particular,
$P$
. In particular,
![]() $X$
has only rational singularities in a neighborhood of
$X$
has only rational singularities in a neighborhood of
![]() $P$
. Therefore, we have
$P$
. Therefore, we have
![]() $P\not \in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
. By the classification of two-dimensional log canonical singularities (see [Reference Kollár and MoriKM, Theorem 4.7] and [Reference MatsukiMa, Theorem 4-6-28]),
$P\not \in \operatorname{Supp}\unicode[STIX]{x1D6E5}$
. By the classification of two-dimensional log canonical singularities (see [Reference Kollár and MoriKM, Theorem 4.7] and [Reference MatsukiMa, Theorem 4-6-28]),
![]() $P\in X$
is a simple elliptic singularity or a cusp singularity (see [Reference Kollár and MoriKM, Note 4.8] and [Reference MatsukiMa, Theorem 4-6-28]). We can check that all the other two-dimensional log canonical singularities are rational singularities (see [Reference MatsukiMa, Remark 4-6-29]). Therefore,
$P\in X$
is a simple elliptic singularity or a cusp singularity (see [Reference Kollár and MoriKM, Note 4.8] and [Reference MatsukiMa, Theorem 4-6-28]). We can check that all the other two-dimensional log canonical singularities are rational singularities (see [Reference MatsukiMa, Remark 4-6-29]). Therefore,
![]() $X$
is Gorenstein at
$X$
is Gorenstein at
![]() $P$
.◻
$P$
.◻
Let us start the proof of Theorem 9.1.
Proof of Theorem 9.1.
We divide the proof into several small steps.
Step 1. In this step, we will prove that
![]() $X$
is Moishezon, that is, the algebraic dimension
$X$
is Moishezon, that is, the algebraic dimension
![]() $a(X)$
of
$a(X)$
of
![]() $X$
is two.
$X$
is two.
Let
![]() $f:Y\rightarrow X$
be the minimal resolution of
$f:Y\rightarrow X$
be the minimal resolution of
![]() $X$
with
$X$
with
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}:=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is log canonical since so is
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is log canonical since so is
![]() $(X,\unicode[STIX]{x1D6E5})$
by assumption. By applying Lemma 4.3 to
$(X,\unicode[STIX]{x1D6E5})$
by assumption. By applying Lemma 4.3 to
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
, we obtain that
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
, we obtain that
![]() $Y$
is a smooth projective surface. This implies that
$Y$
is a smooth projective surface. This implies that
![]() $X$
is Moishezon, that is, the algebraic dimension
$X$
is Moishezon, that is, the algebraic dimension
![]() $a(X)$
of
$a(X)$
of
![]() $X$
is two.
$X$
is two.
Step 2. If
![]() $X$
has only rational singularities, then
$X$
has only rational singularities, then
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial (see Lemma 3.10). In this case, by Lemma 4.1,
$\mathbb{Q}$
-factorial (see Lemma 3.10). In this case, by Lemma 4.1,
![]() $X$
is projective since we have already known that
$X$
is projective since we have already known that
![]() $X$
is Moishezon in Step 1.
$X$
is Moishezon in Step 1.
Therefore, from now on, we may assume that
![]() $X$
has at least one nonrational singular point.
$X$
has at least one nonrational singular point.
Step 3. By applying Theorem 8.4 finitely many times, we may assume that if
![]() $C$
is an irreducible curve on
$C$
is an irreducible curve on
![]() $X$
with
$X$
with
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
, then
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C>0$
, then
![]() $C^{2}\geqslant 0$
holds (see Remark 8.6).
$C^{2}\geqslant 0$
holds (see Remark 8.6).
Step 4. Let
![]() $g:Z\rightarrow X$
be the minimal resolution of nonrational singularities of
$g:Z\rightarrow X$
be the minimal resolution of nonrational singularities of
![]() $X$
. Then we get the following commutative diagram:
$X$
. Then we get the following commutative diagram:

Since
![]() $Z$
has only rational singularities by construction, we see that
$Z$
has only rational singularities by construction, we see that
![]() $Z$
is
$Z$
is
![]() $\mathbb{Q}$
-factorial (see Lemma 3.10). Therefore,
$\mathbb{Q}$
-factorial (see Lemma 3.10). Therefore,
![]() $Z$
is projective by Lemma 4.1 since
$Z$
is projective by Lemma 4.1 since
![]() $Z$
is Moishezon (see Step 1). We put
$Z$
is Moishezon (see Step 1). We put
![]() $K_{Z}+\unicode[STIX]{x1D6E5}_{Z}:=g^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
$K_{Z}+\unicode[STIX]{x1D6E5}_{Z}:=g^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. Then
![]() $\unicode[STIX]{x1D6E5}_{Z}$
is effective by the negativity lemma. Of course,
$\unicode[STIX]{x1D6E5}_{Z}$
is effective by the negativity lemma. Of course,
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
is log canonical. More precisely, by Lemma 9.2, we have
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
is log canonical. More precisely, by Lemma 9.2, we have
![]() $\unicode[STIX]{x1D6E5}_{Z}=\sum _{i}E_{i}+g_{\ast }^{-1}\unicode[STIX]{x1D6E5}$
, where
$\unicode[STIX]{x1D6E5}_{Z}=\sum _{i}E_{i}+g_{\ast }^{-1}\unicode[STIX]{x1D6E5}$
, where
![]() $\operatorname{Exc}(g)=\sum _{i}E_{i}$
. Since
$\operatorname{Exc}(g)=\sum _{i}E_{i}$
. Since
![]() $K_{Z}+\unicode[STIX]{x1D6E5}_{Z}$
never becomes nef by
$K_{Z}+\unicode[STIX]{x1D6E5}_{Z}$
never becomes nef by
![]() $\unicode[STIX]{x1D705}(Z,K_{Z}+\unicode[STIX]{x1D6E5}_{Z})=\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
(see Theorem 7.1), there exists a
$\unicode[STIX]{x1D705}(Z,K_{Z}+\unicode[STIX]{x1D6E5}_{Z})=\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
(see Theorem 7.1), there exists a
![]() $(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
$(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
![]() $R=\mathbb{R}_{{\geqslant}0}[\bar{C}]$
of
$R=\mathbb{R}_{{\geqslant}0}[\bar{C}]$
of
![]() $\overline{\operatorname{NE}}(Z)$
, where
$\overline{\operatorname{NE}}(Z)$
, where
![]() $\bar{C}$
is an irreducible rational curve on
$\bar{C}$
is an irreducible rational curve on
![]() $Z$
.
$Z$
.
Step 5. In this step, we will prove the following claim.
Claim 2. The self-intersection number
![]() $\bar{C}^{2}$
of
$\bar{C}^{2}$
of
![]() $\bar{C}$
is nonnegative, where
$\bar{C}$
is nonnegative, where
![]() $\bar{C}$
is a
$\bar{C}$
is a
![]() $(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal rational curve as in Step 4.
$(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal rational curve as in Step 4.
Proof of Claim 2.
We assume that
![]() $\bar{C}^{2}<0$
holds. Since
$\bar{C}^{2}<0$
holds. Since
![]() $-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot \bar{C}>0$
,
$-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot \bar{C}>0$
,
![]() $\bar{C}$
is not
$\bar{C}$
is not
![]() $g$
-exceptional. If
$g$
-exceptional. If
![]() $C_{X}:=g_{\ast }\bar{C}$
is disjoint from nonrational singularities of
$C_{X}:=g_{\ast }\bar{C}$
is disjoint from nonrational singularities of
![]() $X$
, then we have
$X$
, then we have
![]() $(C_{X})^{2}<0$
and
$(C_{X})^{2}<0$
and
![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C_{X}>0$
because
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C_{X}>0$
because
![]() $g$
is an isomorphism in a neighborhood of
$g$
is an isomorphism in a neighborhood of
![]() $\bar{C}$
. This is a contradiction by Step 3. Therefore,
$\bar{C}$
. This is a contradiction by Step 3. Therefore,
![]() $C_{X}$
passes though at least one nonrational singular point
$C_{X}$
passes though at least one nonrational singular point
![]() $P$
of
$P$
of
![]() $X$
. This implies that
$X$
. This implies that
![]() $C_{X}\not \subset \operatorname{Supp}\unicode[STIX]{x1D6E5}$
by Lemma 9.2. Let
$C_{X}\not \subset \operatorname{Supp}\unicode[STIX]{x1D6E5}$
by Lemma 9.2. Let
![]() $C_{Y}$
be the strict transform of
$C_{Y}$
be the strict transform of
![]() $\bar{C}$
on
$\bar{C}$
on
![]() $Y$
. Then we can easily see that
$Y$
. Then we can easily see that
![]() $(C_{Y})^{2}<0$
holds and that
$(C_{Y})^{2}<0$
holds and that
![]() $C_{Y}$
is not contained in
$C_{Y}$
is not contained in
![]() $\operatorname{Supp}\unicode[STIX]{x1D6E5}_{Y}$
. Thus we obtain that
$\operatorname{Supp}\unicode[STIX]{x1D6E5}_{Y}$
. Thus we obtain that
![]() $-K_{Y}\cdot C_{Y}\geqslant -(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}=-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot \bar{C}>0$
. This means that
$-K_{Y}\cdot C_{Y}\geqslant -(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}=-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot \bar{C}>0$
. This means that
![]() $C_{Y}$
is a
$C_{Y}$
is a
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $Y$
. In particular,
$Y$
. In particular,
![]() $-K_{Y}\cdot C_{Y}=1$
. On the other hand,
$-K_{Y}\cdot C_{Y}=1$
. On the other hand,
![]() $\unicode[STIX]{x1D6E5}_{Y}\cdot C_{Y}\geqslant 1$
since
$\unicode[STIX]{x1D6E5}_{Y}\cdot C_{Y}\geqslant 1$
since
![]() $C_{X}$
passes through a nonrational singular point
$C_{X}$
passes through a nonrational singular point
![]() $P$
and the reduced part of
$P$
and the reduced part of
![]() $\unicode[STIX]{x1D6E5}_{Y}$
contains
$\unicode[STIX]{x1D6E5}_{Y}$
contains
![]() $f^{-1}(P)$
. Thus we have
$f^{-1}(P)$
. Thus we have
![]() $-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}=1-\unicode[STIX]{x1D6E5}_{Y}\cdot C_{Y}\leqslant 0$
. This is a contradiction. Therefore,
$-(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})\cdot C_{Y}=1-\unicode[STIX]{x1D6E5}_{Y}\cdot C_{Y}\leqslant 0$
. This is a contradiction. Therefore,
![]() $\bar{C}^{2}\geqslant 0$
holds.◻
$\bar{C}^{2}\geqslant 0$
holds.◻
Therefore, every
![]() $(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray is spanned by an irreducible rational curve
$(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray is spanned by an irreducible rational curve
![]() $\bar{C}$
with
$\bar{C}$
with
![]() $\bar{C}^{2}\geqslant 0$
.
$\bar{C}^{2}\geqslant 0$
.
We will treat the case where
![]() $\bar{C}^{2}>0$
and
$\bar{C}^{2}>0$
and
![]() $\bar{C}^{2}=0$
in Steps 6 and 7, respectively.
$\bar{C}^{2}=0$
in Steps 6 and 7, respectively.
Step 6. We assume that there exists a
![]() $(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
$(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
![]() $R$
of
$R$
of
![]() $\overline{\operatorname{NE}}(Z)$
spanned by an irreducible rational curve
$\overline{\operatorname{NE}}(Z)$
spanned by an irreducible rational curve
![]() $\bar{C}$
with
$\bar{C}$
with
![]() $\bar{C}^{2}>0$
. In this case, the numerical equivalence class of
$\bar{C}^{2}>0$
. In this case, the numerical equivalence class of
![]() $\bar{C}$
is an interior point of
$\bar{C}$
is an interior point of
![]() $\overline{\operatorname{NE}}(Z)$
(see [Reference Kollár and MoriKM, Corollary 1.21]) and it also generates an extremal ray of
$\overline{\operatorname{NE}}(Z)$
(see [Reference Kollár and MoriKM, Corollary 1.21]) and it also generates an extremal ray of
![]() $\overline{\operatorname{NE}}(Z)$
. Therefore, it is easy to see that
$\overline{\operatorname{NE}}(Z)$
. Therefore, it is easy to see that
![]() $\unicode[STIX]{x1D70C}(Z)=1$
and
$\unicode[STIX]{x1D70C}(Z)=1$
and
![]() $-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
is ample. This is a contradiction because
$-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
is ample. This is a contradiction because
![]() $-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot E=0$
for every
$-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})\cdot E=0$
for every
![]() $g$
-exceptional curve
$g$
-exceptional curve
![]() $E$
on
$E$
on
![]() $Z$
. Thus, this case does not happen.
$Z$
. Thus, this case does not happen.
Step 7. Hence we may assume that there exists a
![]() $(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
$(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
-negative extremal ray
![]() $R$
spanned by an irreducible rational curve
$R$
spanned by an irreducible rational curve
![]() $\bar{C}$
with
$\bar{C}$
with
![]() $\bar{C}^{2}=0$
. Then there exists a surjective morphism
$\bar{C}^{2}=0$
. Then there exists a surjective morphism
![]() $\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
onto a smooth projective curve
$\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
onto a smooth projective curve
![]() $W$
such that
$W$
such that
![]() $\unicode[STIX]{x1D70C}(Z/W)=1$
and
$\unicode[STIX]{x1D70C}(Z/W)=1$
and
![]() $-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
is
$-(K_{Z}+\unicode[STIX]{x1D6E5}_{Z})$
is
![]() $\unicode[STIX]{x1D711}_{R}$
-ample, that is,
$\unicode[STIX]{x1D711}_{R}$
-ample, that is,
![]() $\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
is a Mori fiber space. Without loss of generality, we may assume that
$\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
is a Mori fiber space. Without loss of generality, we may assume that
![]() $\bar{C}$
is a general fiber of
$\bar{C}$
is a general fiber of
![]() $\unicode[STIX]{x1D711}_{R}$
. Since the self-intersection number of any irreducible component of
$\unicode[STIX]{x1D711}_{R}$
. Since the self-intersection number of any irreducible component of
![]() $\operatorname{Exc}(g)$
is negative, every irreducible component of
$\operatorname{Exc}(g)$
is negative, every irreducible component of
![]() $\operatorname{Exc}(g)$
is dominant onto
$\operatorname{Exc}(g)$
is dominant onto
![]() $W$
by
$W$
by
![]() $\unicode[STIX]{x1D711}_{R}$
. Since
$\unicode[STIX]{x1D711}_{R}$
. Since
![]() $-K_{Z}\cdot \bar{C}=2$
and
$-K_{Z}\cdot \bar{C}=2$
and
![]() $\unicode[STIX]{x1D6E5}_{Z}\geqslant \sum _{i}E_{i}=\operatorname{Exc}(g)$
, we can check that
$\unicode[STIX]{x1D6E5}_{Z}\geqslant \sum _{i}E_{i}=\operatorname{Exc}(g)$
, we can check that
![]() $E:=\operatorname{Exc}(g)$
is an irreducible curve such that
$E:=\operatorname{Exc}(g)$
is an irreducible curve such that
![]() $\unicode[STIX]{x1D711}_{R}|_{E}:E\rightarrow W$
is an isomorphism. By the classification of two-dimensional log canonical singularities (see [Reference Kollár and MoriKM, Theorem 4.7] and [Reference MatsukiMa, Theorem 4-6-28]),
$\unicode[STIX]{x1D711}_{R}|_{E}:E\rightarrow W$
is an isomorphism. By the classification of two-dimensional log canonical singularities (see [Reference Kollár and MoriKM, Theorem 4.7] and [Reference MatsukiMa, Theorem 4-6-28]),
![]() $E$
is an elliptic curve and
$E$
is an elliptic curve and
![]() $P$
is a simple elliptic singularity.
$P$
is a simple elliptic singularity.
Claim 3.
![]() $-K_{X}$
is ample, that is,
$-K_{X}$
is ample, that is,
![]() $X$
is Fano. In particular,
$X$
is Fano. In particular,
![]() $X$
is projective.
$X$
is projective.
Proof of Claim 3.
Since
![]() $\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
is a Mori fiber space and
$\unicode[STIX]{x1D711}_{R}:Z\rightarrow W$
is a Mori fiber space and
![]() $-(K_{Z}+E)\cdot \bar{C}=E\cdot \bar{C}=1$
, we obtain that
$-(K_{Z}+E)\cdot \bar{C}=E\cdot \bar{C}=1$
, we obtain that
![]() $-(K_{Z}+E)$
is
$-(K_{Z}+E)$
is
![]() $\mathbb{Q}$
-linearly equivalent to
$\mathbb{Q}$
-linearly equivalent to
![]() $E+\unicode[STIX]{x1D711}_{R}^{\ast }D$
, where
$E+\unicode[STIX]{x1D711}_{R}^{\ast }D$
, where
![]() $D$
is some
$D$
is some
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $W$
. We note that
$W$
. We note that
![]() $\deg D=-E^{2}>0$
since
$\deg D=-E^{2}>0$
since
![]() $(E+\unicode[STIX]{x1D711}_{R}^{\ast }D)\cdot E=-(K_{Z}+E)\cdot E=0$
. Thus, we have
$(E+\unicode[STIX]{x1D711}_{R}^{\ast }D)\cdot E=-(K_{Z}+E)\cdot E=0$
. Thus, we have
![]() $\unicode[STIX]{x1D705}(Z,-(K_{Z}+E))\geqslant 0$
. Since
$\unicode[STIX]{x1D705}(Z,-(K_{Z}+E))\geqslant 0$
. Since
![]() $K_{Z}+E=g^{\ast }K_{X}$
, we obtain
$K_{Z}+E=g^{\ast }K_{X}$
, we obtain
![]() $\unicode[STIX]{x1D705}(X,-K_{X})=\unicode[STIX]{x1D705}(Z,-(K_{Z}+E))\geqslant 0$
. We take any irreducible curve
$\unicode[STIX]{x1D705}(X,-K_{X})=\unicode[STIX]{x1D705}(Z,-(K_{Z}+E))\geqslant 0$
. We take any irreducible curve
![]() $C$
on
$C$
on
![]() $X$
. Let
$X$
. Let
![]() $C^{\prime }$
be the strict transform of
$C^{\prime }$
be the strict transform of
![]() $C$
on
$C$
on
![]() $Z$
. Then
$Z$
. Then
![]() $-K_{X}\cdot C=-(K_{Z}+E)\cdot C^{\prime }=(E+\unicode[STIX]{x1D711}_{R}^{\ast }D)\cdot C^{\prime }>0$
since
$-K_{X}\cdot C=-(K_{Z}+E)\cdot C^{\prime }=(E+\unicode[STIX]{x1D711}_{R}^{\ast }D)\cdot C^{\prime }>0$
since
![]() $C^{\prime }\neq E$
. Thus, we obtain that
$C^{\prime }\neq E$
. Thus, we obtain that
![]() $-K_{X}$
is ample by Nakai–Moishezon’s ampleness criterion for algebraic spaces (see [Reference Pascul GainzaP, (1.4) Theorem]).◻
$-K_{X}$
is ample by Nakai–Moishezon’s ampleness criterion for algebraic spaces (see [Reference Pascul GainzaP, (1.4) Theorem]).◻
Thus we see that
![]() $X$
is projective when
$X$
is projective when
![]() $X$
has at least one nonrational singular point.
$X$
has at least one nonrational singular point.
Therefore, we obtain that
![]() $X$
is always projective if
$X$
is always projective if
![]() $(X,\unicode[STIX]{x1D6E5})$
is a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
is a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
.◻
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
.◻
Remark 9.3. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
$(X,\unicode[STIX]{x1D6E5})$
be a log canonical surface in Fujiki’s class
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
. The proof of Theorem 9.1 shows that if
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
. The proof of Theorem 9.1 shows that if
![]() $X$
has nonrational singularities, then
$X$
has nonrational singularities, then
![]() $X$
has one simple elliptic singularity and no cusp singularities.
$X$
has one simple elliptic singularity and no cusp singularities.
By Theorem 9.1, we can freely apply the minimal model theory of projective log canonical surfaces established in [Reference FujinoFn4] to log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
with negative Kodaira dimension.
${\mathcal{C}}$
with negative Kodaira dimension.
Remark 9.4. We can construct a complete nonprojective log canonical algebraic surface
![]() $(X,\unicode[STIX]{x1D6E5})$
with
$(X,\unicode[STIX]{x1D6E5})$
with
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. For some examples, see Section 12. Therefore, the assumption
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. For some examples, see Section 12. Therefore, the assumption
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
is indispensable in Theorem 9.1.
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})=-\infty$
is indispensable in Theorem 9.1.
10 Proof of Theorem 1.5
In this section, we prove Theorem 1.5, that is, the minimal model theory for log canonical surfaces in Fujiki’s class
![]() ${\mathcal{C}}$
. We give a detailed proof for the reader’s convenience although it is essentially the same as that of Theorem 1.1.
${\mathcal{C}}$
. We give a detailed proof for the reader’s convenience although it is essentially the same as that of Theorem 1.1.
Proof of Theorem 1.5.
If
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\geqslant 0$
for every curve
![]() $C$
on
$C$
on
![]() $X$
, then
$X$
, then
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by Corollary 7.7. So
$K_{X}+\unicode[STIX]{x1D6E5}$
is semiample by Corollary 7.7. So
![]() $(X,\unicode[STIX]{x1D6E5})$
is itself a good minimal model of
$(X,\unicode[STIX]{x1D6E5})$
is itself a good minimal model of
![]() $(X,\unicode[STIX]{x1D6E5})$
. Therefore, we may assume that
$(X,\unicode[STIX]{x1D6E5})$
. Therefore, we may assume that
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
for some curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
for some curve
![]() $C$
on
$C$
on
![]() $X$
. If
$X$
. If
![]() $X$
is projective, then we can run the minimal model program for projective log canonical surfaces and finally get a good minimal model or a Mori fiber space (see [Reference FujinoFn4]). Thus we may assume that
$X$
is projective, then we can run the minimal model program for projective log canonical surfaces and finally get a good minimal model or a Mori fiber space (see [Reference FujinoFn4]). Thus we may assume that
![]() $X$
is not projective. By Theorem 9.1, we obtain
$X$
is not projective. By Theorem 9.1, we obtain
![]() $\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Therefore, we have an effective Cartier divisor
$\unicode[STIX]{x1D705}(X,K_{X}+\unicode[STIX]{x1D6E5})\geqslant 0$
. Therefore, we have an effective Cartier divisor
![]() $D\in |m(K_{X}+\unicode[STIX]{x1D6E5})|$
for some positive divisible integer
$D\in |m(K_{X}+\unicode[STIX]{x1D6E5})|$
for some positive divisible integer
![]() $m$
. Since
$m$
. Since
![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
for some curve
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
for some curve
![]() $C$
on
$C$
on
![]() $X$
,
$X$
,
![]() $C$
is an irreducible component of
$C$
is an irreducible component of
![]() $\operatorname{Supp}D$
such that the self-intersection number
$\operatorname{Supp}D$
such that the self-intersection number
![]() $C^{2}$
is negative. We apply the contraction theorem, Theorem 8.4. Since there are only finitely many irreducible components of
$C^{2}$
is negative. We apply the contraction theorem, Theorem 8.4. Since there are only finitely many irreducible components of
![]() $\operatorname{Supp}D$
, we finally get
$\operatorname{Supp}D$
, we finally get
![]() $(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
such that
$(X^{\ast },\unicode[STIX]{x1D6E5}^{\ast })$
such that
![]() $K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample after finitely many contractions.
$K_{X^{\ast }}+\unicode[STIX]{x1D6E5}^{\ast }$
is semiample after finitely many contractions.
Since
![]() $R^{1}{\unicode[STIX]{x1D711}_{i}}_{\ast }{\mathcal{O}}_{X_{i}}=0$
by Theorem 11.3,
$R^{1}{\unicode[STIX]{x1D711}_{i}}_{\ast }{\mathcal{O}}_{X_{i}}=0$
by Theorem 11.3,
![]() $X_{i}$
has only rational singularities if and only if so does
$X_{i}$
has only rational singularities if and only if so does
![]() $X_{i+1}$
by Lemma 2.8. Therefore, we have (2).
$X_{i+1}$
by Lemma 2.8. Therefore, we have (2).
Since
![]() $\unicode[STIX]{x1D711}_{i}$
is projective by construction,
$\unicode[STIX]{x1D711}_{i}$
is projective by construction,
![]() $X_{i}$
is projective when so is
$X_{i}$
is projective when so is
![]() $X_{i+1}$
. If
$X_{i+1}$
. If
![]() $X_{i}$
is projective, then
$X_{i}$
is projective, then
![]() $\unicode[STIX]{x1D711}_{i}$
is the usual contraction morphism associated with a
$\unicode[STIX]{x1D711}_{i}$
is the usual contraction morphism associated with a
![]() $(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$
-negative extremal ray (see Remark 8.5). This implies that
$(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})$
-negative extremal ray (see Remark 8.5). This implies that
![]() $X_{i+1}$
is also projective. Thus we have (1).
$X_{i+1}$
is also projective. Thus we have (1).
Since
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})\simeq \mathbb{P}^{1}$
,
$\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})\simeq \mathbb{P}^{1}$
,
![]() $C_{i}=\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})$
is
$C_{i}=\operatorname{Exc}(\unicode[STIX]{x1D711}_{i})$
is
![]() $\mathbb{Q}$
-Cartier, and
$\mathbb{Q}$
-Cartier, and
![]() $-C_{i}$
is
$-C_{i}$
is
![]() $\unicode[STIX]{x1D711}_{i}$
-ample, we can easily check (3) by Theorem 3.11.◻
$\unicode[STIX]{x1D711}_{i}$
-ample, we can easily check (3) by Theorem 3.11.◻
11 Appendix: Vanishing theorems
In this section, we quickly explain some vanishing theorems for the reader’s convenience. Fortunately, we do not need difficult analytic methods. They follow from elementary arguments.
Let us start with the following vanishing theorem. We learned it from [Reference Kollár and KovácsKK] (see [Reference KollárK2, Theorem 10.4]).
Theorem 11.1. (Relative vanishing theorem)
Let
![]() $\unicode[STIX]{x1D711}:V\rightarrow W$
be a proper bimeromorphic morphism from a smooth analytic surface to a normal analytic surface
$\unicode[STIX]{x1D711}:V\rightarrow W$
be a proper bimeromorphic morphism from a smooth analytic surface to a normal analytic surface
![]() $W$
. Assume that there exists a point
$W$
. Assume that there exists a point
![]() $P\in W$
such that
$P\in W$
such that
![]() $\unicode[STIX]{x1D711}$
is an isomorphism over
$\unicode[STIX]{x1D711}$
is an isomorphism over
![]() $W\setminus P$
. Let
$W\setminus P$
. Let
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711})=\sum _{i}E_{i}$
be the irreducible decomposition of the
$\operatorname{Exc}(\unicode[STIX]{x1D711})=\sum _{i}E_{i}$
be the irreducible decomposition of the
![]() $\unicode[STIX]{x1D711}$
-exceptional locus
$\unicode[STIX]{x1D711}$
-exceptional locus
![]() $\operatorname{Exc}(\unicode[STIX]{x1D711})$
. Let
$\operatorname{Exc}(\unicode[STIX]{x1D711})$
. Let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $V$
, let
$V$
, let
![]() $N$
be a
$N$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $V$
, and let
$V$
, and let
![]() $E=\sum _{i}b_{i}E_{i}$
be an effective
$E=\sum _{i}b_{i}E_{i}$
be an effective
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $V$
. Assume that
$V$
. Assume that
![]() $N\cdot E_{i}\geqslant 0$
and
$N\cdot E_{i}\geqslant 0$
and
![]() ${\mathcal{L}}\cdot E_{i}=(K_{V}+E+N)\cdot E_{i}$
hold for every
${\mathcal{L}}\cdot E_{i}=(K_{V}+E+N)\cdot E_{i}$
hold for every
![]() $i$
. We further assume that one of the following conditions holds.
$i$
. We further assume that one of the following conditions holds.
-
(1)
 $0\leqslant b_{i}<1$
for every
$0\leqslant b_{i}<1$
for every
 $i$
.
$i$
. -
(2)
 $0<b_{i}\leqslant 1$
for every
$0<b_{i}\leqslant 1$
for every
 $i$
and there exists some
$i$
and there exists some
 $j$
such that
$j$
such that
 $b_{j}\neq 1$
.
$b_{j}\neq 1$
. -
(3)
 $0<b_{i}\leqslant 1$
for every
$0<b_{i}\leqslant 1$
for every
 $i$
and there exists some
$i$
and there exists some
 $j$
such that
$j$
such that
 $N\cdot E_{j}>0$
.
$N\cdot E_{j}>0$
.
Then
![]() $R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}=0$
holds for every
$R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}=0$
holds for every
![]() $i>0$
.
$i>0$
.
Theorem 11.1(1) is a special case of the Kawamata–Viehweg vanishing theorem. Note that condition (1) is most useful.
Remark 11.2. In Theorem 11.1, it is sufficient to assume that
![]() $N$
is a
$N$
is a
![]() $\mathbb{Q}$
-line bundle on
$\mathbb{Q}$
-line bundle on
![]() $V$
, that is, a finite
$V$
, that is, a finite
![]() $\mathbb{Q}$
-linear combination of some line bundles on
$\mathbb{Q}$
-linear combination of some line bundles on
![]() $V$
such that
$V$
such that
![]() $N\cdot E_{i}\geqslant 0$
and
$N\cdot E_{i}\geqslant 0$
and
![]() ${\mathcal{L}}\cdot E_{i}=(K_{V}+E)\cdot E_{i}+N\cdot E_{i}$
hold for every
${\mathcal{L}}\cdot E_{i}=(K_{V}+E)\cdot E_{i}+N\cdot E_{i}$
hold for every
![]() $i$
.
$i$
.
Proof of Theorem 11.1.
Let us consider
![]() $Z=\sum _{i}r_{i}E_{i}$
, where
$Z=\sum _{i}r_{i}E_{i}$
, where
![]() $r_{i}$
is a nonnegative integer for every
$r_{i}$
is a nonnegative integer for every
![]() $i$
. Although [Reference KollárK2, Theorem 10.4] is formulated and proved for two-dimensional regular schemes, the proof works for two-dimensional complex manifolds. Therefore, by the proof of [Reference KollárK2, Theorem 10.4], we obtain
$i$
. Although [Reference KollárK2, Theorem 10.4] is formulated and proved for two-dimensional regular schemes, the proof works for two-dimensional complex manifolds. Therefore, by the proof of [Reference KollárK2, Theorem 10.4], we obtain
![]() $H^{1}(Z,{\mathcal{L}}\otimes {\mathcal{O}}_{Z})=0$
(see also [Reference Kollár and KovácsKK, 2.2.1 Theorem]). Hence, by using the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]), we get
$H^{1}(Z,{\mathcal{L}}\otimes {\mathcal{O}}_{Z})=0$
(see also [Reference Kollár and KovácsKK, 2.2.1 Theorem]). Hence, by using the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]), we get
![]() $R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}=0$
for every
$R^{i}\unicode[STIX]{x1D711}_{\ast }{\mathcal{L}}=0$
for every
![]() $i>0$
(see also [Reference Kollár and KovácsKK, 2.2.5 Corollary]).◻
$i>0$
(see also [Reference Kollár and KovácsKK, 2.2.5 Corollary]).◻
As an application of Theorem 11.1, we can prove the following vanishing theorem, which is a Kawamata–Viehweg vanishing theorem for proper bimeromorphic morphisms between surfaces.
Theorem 11.3. Let
![]() $X$
be a normal analytic surface, and let
$X$
be a normal analytic surface, and let
![]() $\unicode[STIX]{x1D6E5}$
be an effective
$\unicode[STIX]{x1D6E5}$
be an effective
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier. Let
$\mathbb{Q}$
-Cartier. Let
![]() $f:X\rightarrow Y$
be a proper bimeromorphic morphism onto a normal analytic surface
$f:X\rightarrow Y$
be a proper bimeromorphic morphism onto a normal analytic surface
![]() $Y$
. Let
$Y$
. Let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $X$
, and let
$X$
, and let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-Cartier Weil divisor on
$\mathbb{Q}$
-Cartier Weil divisor on
![]() $X$
. Assume that one of the following conditions holds.
$X$
. Assume that one of the following conditions holds.
-
(1)
 ${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C>0$
for every
${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C>0$
for every
 $f$
-exceptional curve
$f$
-exceptional curve
 $C$
on
$C$
on
 $X$
and the coefficients of
$X$
and the coefficients of
 $\unicode[STIX]{x1D6E5}$
are less than or equal to one.
$\unicode[STIX]{x1D6E5}$
are less than or equal to one. -
(2)
 ${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C\geqslant 0$
for every
${\mathcal{L}}\cdot C+(D-(K_{X}+\unicode[STIX]{x1D6E5}))\cdot C\geqslant 0$
for every
 $f$
-exceptional curve
$f$
-exceptional curve
 $C$
on
$C$
on
 $X$
and the coefficients of
$X$
and the coefficients of
 $\unicode[STIX]{x1D6E5}$
are less than one.
$\unicode[STIX]{x1D6E5}$
are less than one.
Then
![]() $R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
holds for every
$R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
holds for every
![]() $i>0$
.
$i>0$
.
Let us prove Theorem 11.3. The following proof is essentially the same as that of [Reference Fujino and TanakaFT, Theorem 6.2].
Proof of Theorem 11.3.
We divide the proof into small steps.
Step 1. Without loss of generality, we can freely shrink
![]() $Y$
and assume that
$Y$
and assume that
![]() $Y$
is a small relatively compact Stein open subset of normal analytic surface. We may further assume that
$Y$
is a small relatively compact Stein open subset of normal analytic surface. We may further assume that
![]() $f$
is an isomorphism outside
$f$
is an isomorphism outside
![]() $P\in Y$
and
$P\in Y$
and
![]() $f^{-1}(P)$
is one-dimensional.
$f^{-1}(P)$
is one-dimensional.
Step 2. When
![]() $\lfloor \unicode[STIX]{x1D6E5}\rfloor \neq 0$
, we can take an
$\lfloor \unicode[STIX]{x1D6E5}\rfloor \neq 0$
, we can take an
![]() $f$
-ample Cartier divisor
$f$
-ample Cartier divisor
![]() $H$
(see (1)). Then we can find an effective
$H$
(see (1)). Then we can find an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
on
$\unicode[STIX]{x1D6E5}^{\prime }$
on
![]() $X$
such that
$X$
such that
![]() $\lfloor \unicode[STIX]{x1D6E5}^{\prime }\rfloor =0$
and that
$\lfloor \unicode[STIX]{x1D6E5}^{\prime }\rfloor =0$
and that
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
is
$\unicode[STIX]{x1D6E5}^{\prime }$
is
![]() $\mathbb{Q}$
-linearly equivalent to
$\mathbb{Q}$
-linearly equivalent to
![]() $\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}H$
for some
$\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D700}H$
for some
![]() $0<\unicode[STIX]{x1D700}\ll 1$
. More precisely, we take a general member
$0<\unicode[STIX]{x1D700}\ll 1$
. More precisely, we take a general member
![]() $B$
of
$B$
of
![]() $|\lfloor \unicode[STIX]{x1D6E5}\rfloor +mH|$
for some large positive integer
$|\lfloor \unicode[STIX]{x1D6E5}\rfloor +mH|$
for some large positive integer
![]() $m$
and put
$m$
and put
By replacing
![]() $\unicode[STIX]{x1D6E5}$
with
$\unicode[STIX]{x1D6E5}$
with
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
, we can always assume that
$\unicode[STIX]{x1D6E5}^{\prime }$
, we can always assume that
![]() $\lfloor \unicode[STIX]{x1D6E5}\rfloor =0$
.
$\lfloor \unicode[STIX]{x1D6E5}\rfloor =0$
.
Step 3. Let
![]() $\unicode[STIX]{x1D711}:Z\rightarrow X$
be the minimal resolution of
$\unicode[STIX]{x1D711}:Z\rightarrow X$
be the minimal resolution of
![]() $X$
. We set
$X$
. We set
![]() $K_{Z}+\unicode[STIX]{x1D6E5}_{Z}:=\unicode[STIX]{x1D711}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. We note that
$K_{Z}+\unicode[STIX]{x1D6E5}_{Z}:=\unicode[STIX]{x1D711}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. We note that
![]() $\unicode[STIX]{x1D6E5}_{Z}$
is effective by the negativity lemma. We note that
$\unicode[STIX]{x1D6E5}_{Z}$
is effective by the negativity lemma. We note that
We put
![]() $\unicode[STIX]{x1D6E9}:=\unicode[STIX]{x1D6E5}_{Z}+\{-\unicode[STIX]{x1D711}^{\ast }D\}$
. Then
$\unicode[STIX]{x1D6E9}:=\unicode[STIX]{x1D6E5}_{Z}+\{-\unicode[STIX]{x1D711}^{\ast }D\}$
. Then
We note that we can write
![]() $\{\unicode[STIX]{x1D6E9}\}=E+M$
, where
$\{\unicode[STIX]{x1D6E9}\}=E+M$
, where
![]() $E$
is a
$E$
is a
![]() $\unicode[STIX]{x1D711}$
-exceptional effective
$\unicode[STIX]{x1D711}$
-exceptional effective
![]() $\mathbb{Q}$
-divisor with
$\mathbb{Q}$
-divisor with
![]() $\lfloor E\rfloor =0$
and
$\lfloor E\rfloor =0$
and
![]() $M$
is an effective
$M$
is an effective
![]() $\mathbb{Q}$
-divisor such that every irreducible component of
$\mathbb{Q}$
-divisor such that every irreducible component of
![]() $M$
is not
$M$
is not
![]() $\unicode[STIX]{x1D711}$
-exceptional. Let us consider
$\unicode[STIX]{x1D711}$
-exceptional. Let us consider
By Theorem 11.1, we have
Therefore, we get the following short exact sequence:
By construction,
![]() $\lfloor \unicode[STIX]{x1D6E9}\rfloor$
is
$\lfloor \unicode[STIX]{x1D6E9}\rfloor$
is
![]() $\unicode[STIX]{x1D711}$
-exceptional. Therefore,
$\unicode[STIX]{x1D711}$
-exceptional. Therefore,
![]() ${\mathcal{L}}\otimes \unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{\lfloor \unicode[STIX]{x1D6E9}\rfloor }(\lceil \unicode[STIX]{x1D711}^{\ast }D\rceil )$
is a skyscraper sheaf on
${\mathcal{L}}\otimes \unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{\lfloor \unicode[STIX]{x1D6E9}\rfloor }(\lceil \unicode[STIX]{x1D711}^{\ast }D\rceil )$
is a skyscraper sheaf on
![]() $X$
. Thus we obtain the following surjection:
$X$
. Thus we obtain the following surjection:
since
![]() $\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{Z}(\lceil \unicode[STIX]{x1D711}^{\ast }D\rceil )\simeq {\mathcal{O}}_{X}(D)$
. By the Leray spectral sequence, we have
$\unicode[STIX]{x1D711}_{\ast }{\mathcal{O}}_{Z}(\lceil \unicode[STIX]{x1D711}^{\ast }D\rceil )\simeq {\mathcal{O}}_{X}(D)$
. By the Leray spectral sequence, we have
As before, we can write
![]() $\{\unicode[STIX]{x1D6E9}\}=E^{\prime }+M^{\prime }$
, where
$\{\unicode[STIX]{x1D6E9}\}=E^{\prime }+M^{\prime }$
, where
![]() $E^{\prime }$
is a
$E^{\prime }$
is a
![]() $f\circ \unicode[STIX]{x1D711}$
-exceptional effective
$f\circ \unicode[STIX]{x1D711}$
-exceptional effective
![]() $\mathbb{Q}$
-divisor with
$\mathbb{Q}$
-divisor with
![]() $\lfloor E^{\prime }\rfloor =0$
and
$\lfloor E^{\prime }\rfloor =0$
and
![]() $M^{\prime }$
is an effective
$M^{\prime }$
is an effective
![]() $\mathbb{Q}$
-divisor such that every irreducible component of
$\mathbb{Q}$
-divisor such that every irreducible component of
![]() $M^{\prime }$
is not
$M^{\prime }$
is not
![]() $f\circ \unicode[STIX]{x1D711}$
-exceptional. By Theorem 11.1, we know that
$f\circ \unicode[STIX]{x1D711}$
-exceptional. By Theorem 11.1, we know that
This implies that
by (11.2). By surjection (11.1), we get
![]() $R^{1}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
.
$R^{1}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
.
Step 4. Since
![]() $f^{-1}(P)$
is one-dimensional,
$f^{-1}(P)$
is one-dimensional,
![]() $R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
for every
$R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
for every
![]() $i>2$
by the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]).
$i>2$
by the theorem on formal functions for proper morphisms between analytic spaces (see [Reference Bănică and StănăşilăBS, Chapter VI, Corollary 4.7]).
Therefore, we have
![]() $R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
for every
$R^{i}f_{\ast }({\mathcal{L}}\otimes {\mathcal{O}}_{X}(D))=0$
for every
![]() $i>0$
.◻
$i>0$
.◻
We close this section with an obvious remark.
Remark 11.4. Theorems 11.1 and 11.3 can be formulated and proved easily for proper birational morphisms between algebraic surfaces defined over any algebraically closed field. Therefore, we can formulate and prove Theorem 3.11 for projective birational morphisms between (not necessarily complete) algebraic surfaces defined over any algebraically closed field. This is because the proof of Theorem 3.11 only needs the vanishing theorem, Theorem 11.3.
12 Appendix: Complete nonprojective algebraic surfaces
In this section, we construct some examples of complete nonprojective log canonical algebraic surfaces. From Example 12.1 to Example 12.5, we will work over
![]() $\mathbb{C}$
, the complex number field.
$\mathbb{C}$
, the complex number field.
Let us start with Kollár’s example. Although it is not stated explicitly in [Reference KollárK1], it does not satisfy Kleiman’s ampleness criterion. We note that the arguments in Example 12.3 help the reader understand Example 12.1. Therefore, we do not explain the details of Kollár’s example.
Example 12.1. ([Reference KollárK1, Aside 3.46])
In this example, we will freely use Kollár’s notation in [Reference KollárK1, Aside 3.46]. In [Reference KollárK1, Aside 3.46], we assume that
![]() $C$
is an elliptic curve. Then the surface
$C$
is an elliptic curve. Then the surface
![]() $S$
constructed in [Reference KollárK1, Aside 3.46] is a complete nonprojective algebraic surface with two simple elliptic singularities. In particular,
$S$
constructed in [Reference KollárK1, Aside 3.46] is a complete nonprojective algebraic surface with two simple elliptic singularities. In particular,
![]() $S$
is Gorenstein and log canonical. Let
$S$
is Gorenstein and log canonical. Let
![]() $C^{\prime }$
be the strict transform of
$C^{\prime }$
be the strict transform of
![]() $\{1\}\times C$
on
$\{1\}\times C$
on
![]() $S$
. Then we have
$S$
. Then we have
![]() $\operatorname{Pic}(S)=\mathbb{Z}{\mathcal{O}}_{S}(C^{\prime })$
. We can directly check that
$\operatorname{Pic}(S)=\mathbb{Z}{\mathcal{O}}_{S}(C^{\prime })$
. We can directly check that
![]() $\unicode[STIX]{x1D70B}_{1}(S)=\{1\}$
, that is,
$\unicode[STIX]{x1D70B}_{1}(S)=\{1\}$
, that is,
![]() $S$
is simply connected,
$S$
is simply connected,
![]() $K_{S}\sim 0$
,
$K_{S}\sim 0$
,
![]() $H^{1}(S,{\mathcal{O}}_{S})=0$
, and
$H^{1}(S,{\mathcal{O}}_{S})=0$
, and
![]() $H^{2}(S,{\mathcal{O}}_{S})=\mathbb{C}$
. Therefore,
$H^{2}(S,{\mathcal{O}}_{S})=\mathbb{C}$
. Therefore,
![]() $S$
is a log canonical Calabi–Yau algebraic surface. Of course, we have
$S$
is a log canonical Calabi–Yau algebraic surface. Of course, we have
![]() $\unicode[STIX]{x1D705}(S,K_{S})=0$
. Let
$\unicode[STIX]{x1D705}(S,K_{S})=0$
. Let
![]() $F$
be a general fiber of the second projection
$F$
be a general fiber of the second projection
![]() $\mathbb{P}^{1}\times C\rightarrow C$
, and let
$\mathbb{P}^{1}\times C\rightarrow C$
, and let
![]() $F^{\prime }$
be the strict transform of
$F^{\prime }$
be the strict transform of
![]() $F$
on
$F$
on
![]() $S$
. Then
$S$
. Then
![]() $\overline{\operatorname{NE}}(S)=\mathbb{R}_{{\geqslant}0}[F^{\prime }]$
holds. We note that
$\overline{\operatorname{NE}}(S)=\mathbb{R}_{{\geqslant}0}[F^{\prime }]$
holds. We note that
![]() ${\mathcal{O}}_{S}(C^{\prime })$
is positive on
${\mathcal{O}}_{S}(C^{\prime })$
is positive on
![]() $\overline{\operatorname{NE}}(S)\setminus \{0\}$
. However,
$\overline{\operatorname{NE}}(S)\setminus \{0\}$
. However,
![]() $C^{\prime }$
is nef but is not ample. This means that Kleiman’s ampleness criterion does not hold for
$C^{\prime }$
is nef but is not ample. This means that Kleiman’s ampleness criterion does not hold for
![]() $S$
.
$S$
.
Let us prepare an easy lemma.
Lemma 12.2. Let
![]() $C$
be a smooth projective curve, and let
$C$
be a smooth projective curve, and let
![]() ${\mathcal{A}}$
be an ample line bundle on
${\mathcal{A}}$
be an ample line bundle on
![]() $C$
. We consider
$C$
. We consider
![]() $\unicode[STIX]{x1D70B}:X:=\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}})\rightarrow C$
. Then
$\unicode[STIX]{x1D70B}:X:=\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}})\rightarrow C$
. Then
![]() ${\mathcal{O}}_{X}(1)\simeq {\mathcal{O}}_{X}(C_{+})$
is semiample, where
${\mathcal{O}}_{X}(1)\simeq {\mathcal{O}}_{X}(C_{+})$
is semiample, where
![]() $C_{+}:=\mathbb{P}_{C}({\mathcal{A}})$
is the positive section of
$C_{+}:=\mathbb{P}_{C}({\mathcal{A}})$
is the positive section of
![]() $\unicode[STIX]{x1D70B}$
, and the complete linear system
$\unicode[STIX]{x1D70B}$
, and the complete linear system
![]() $|{\mathcal{O}}_{X}(m)|$
only contracts the negative section
$|{\mathcal{O}}_{X}(m)|$
only contracts the negative section
![]() $C_{-}:=\mathbb{P}_{C}({\mathcal{O}}_{C})$
of
$C_{-}:=\mathbb{P}_{C}({\mathcal{O}}_{C})$
of
![]() $\unicode[STIX]{x1D70B}$
to a point for some sufficiently large positive integer
$\unicode[STIX]{x1D70B}$
to a point for some sufficiently large positive integer
![]() $m$
.
$m$
.
Proof. We can easily check that
![]() ${\mathcal{O}}_{X}(1)$
is semiample (see [Reference LazarsfeldLa, Lemma 2.3.2]). We note that
${\mathcal{O}}_{X}(1)$
is semiample (see [Reference LazarsfeldLa, Lemma 2.3.2]). We note that
![]() $C_{-}\cdot {\mathcal{O}}_{X}(1)=0$
and
$C_{-}\cdot {\mathcal{O}}_{X}(1)=0$
and
![]() $D\cdot {\mathcal{O}}_{X}(1)>0$
for every irreducible curve
$D\cdot {\mathcal{O}}_{X}(1)>0$
for every irreducible curve
![]() $D$
on
$D$
on
![]() $X$
with
$X$
with
![]() $D\neq C_{-}$
. Therefore, the complete linear system
$D\neq C_{-}$
. Therefore, the complete linear system
![]() $|{\mathcal{O}}_{X}(m)|$
contracts
$|{\mathcal{O}}_{X}(m)|$
contracts
![]() $C_{-}$
only.◻
$C_{-}$
only.◻
Let us construct complete nonprojective normal algebraic surfaces
![]() $S$
with
$S$
with
![]() $\operatorname{Pic}(S)=\{0\}$
. The following construction was suggested by Kento Fujita.
$\operatorname{Pic}(S)=\{0\}$
. The following construction was suggested by Kento Fujita.
Example 12.3. Let
![]() $C$
be a smooth projective curve of genus
$C$
be a smooth projective curve of genus
![]() ${\geqslant}1$
, and let
${\geqslant}1$
, and let
![]() ${\mathcal{L}}={\mathcal{O}}_{C}(L)$
be a nontorsion element of
${\mathcal{L}}={\mathcal{O}}_{C}(L)$
be a nontorsion element of
![]() $\operatorname{Pic}^{0}(C)$
. We consider
$\operatorname{Pic}^{0}(C)$
. We consider
![]() $\unicode[STIX]{x1D70B}:V:=\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})\rightarrow C$
. Let
$\unicode[STIX]{x1D70B}:V:=\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})\rightarrow C$
. Let
![]() $C_{1}$
(resp.
$C_{1}$
(resp.
![]() $C_{2}$
) be the section of
$C_{2}$
) be the section of
![]() $\unicode[STIX]{x1D70B}$
corresponding to
$\unicode[STIX]{x1D70B}$
corresponding to
![]() ${\mathcal{O}}_{C}\oplus {\mathcal{L}}\rightarrow {\mathcal{O}}_{C}\rightarrow 0$
(resp.
${\mathcal{O}}_{C}\oplus {\mathcal{L}}\rightarrow {\mathcal{O}}_{C}\rightarrow 0$
(resp.
![]() ${\mathcal{O}}_{C}\oplus {\mathcal{L}}\rightarrow {\mathcal{L}}\rightarrow 0$
). We note that
${\mathcal{O}}_{C}\oplus {\mathcal{L}}\rightarrow {\mathcal{L}}\rightarrow 0$
). We note that
![]() $C_{2}\sim \unicode[STIX]{x1D70B}^{\ast }L+C_{1}$
holds. We take an arbitrary point
$C_{2}\sim \unicode[STIX]{x1D70B}^{\ast }L+C_{1}$
holds. We take an arbitrary point
![]() $P\in C$
and blow up
$P\in C$
and blow up
![]() $P_{1}$
and
$P_{1}$
and
![]() $P_{2}$
, where
$P_{2}$
, where
![]() $P_{i}:=\unicode[STIX]{x1D70B}^{-1}(P)\cap C_{i}$
for
$P_{i}:=\unicode[STIX]{x1D70B}^{-1}(P)\cap C_{i}$
for
![]() $i=1,2$
, to get
$i=1,2$
, to get
![]() $p:W\rightarrow V$
. Let
$p:W\rightarrow V$
. Let
![]() $C_{i}^{\prime }$
be the strict transform of
$C_{i}^{\prime }$
be the strict transform of
![]() $C_{i}$
on
$C_{i}$
on
![]() $W$
for
$W$
for
![]() $i=1,2$
, and let
$i=1,2$
, and let
![]() $\ell$
be the strict transform of
$\ell$
be the strict transform of
![]() $\unicode[STIX]{x1D70B}^{-1}(P)$
on
$\unicode[STIX]{x1D70B}^{-1}(P)$
on
![]() $W$
. Let
$W$
. Let
![]() $E_{i}$
denote the
$E_{i}$
denote the
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $W$
with
$W$
with
![]() $p(E_{i})=P_{i}$
for
$p(E_{i})=P_{i}$
for
![]() $i=1,2$
. We put
$i=1,2$
. We put
We note that
![]() $C_{i}^{\prime }\subset U_{i}$
for
$C_{i}^{\prime }\subset U_{i}$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\ell \subset U_{0}$
by construction. Then we can realize
$\ell \subset U_{0}$
by construction. Then we can realize
![]() $U_{i}$
as a Zariski open subset of
$U_{i}$
as a Zariski open subset of
![]() $\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}}_{i})$
with
$\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}}_{i})$
with
![]() $\deg {\mathcal{A}}_{i}=1$
such that
$\deg {\mathcal{A}}_{i}=1$
such that
![]() $C_{i}^{\prime }$
corresponds to the negative section
$C_{i}^{\prime }$
corresponds to the negative section
![]() $C_{-}$
on
$C_{-}$
on
![]() $\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}}_{i})$
for
$\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{A}}_{i})$
for
![]() $i=1,2$
. By Lemma 12.2, we can construct a projective birational morphism
$i=1,2$
. By Lemma 12.2, we can construct a projective birational morphism
![]() $U_{i}\rightarrow S_{i}$
onto a normal quasi-projective surface
$U_{i}\rightarrow S_{i}$
onto a normal quasi-projective surface
![]() $S_{i}$
such that the exceptional locus is
$S_{i}$
such that the exceptional locus is
![]() $C_{i}^{\prime }$
for
$C_{i}^{\prime }$
for
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $\ell$
is a
$\ell$
is a
![]() $(-2)$
-curve on a smooth projective surface
$(-2)$
-curve on a smooth projective surface
![]() $W$
, we can construct a projective birational morphism
$W$
, we can construct a projective birational morphism
![]() $U_{0}\rightarrow S_{0}$
onto a normal quasi-projective surface
$U_{0}\rightarrow S_{0}$
onto a normal quasi-projective surface
![]() $S_{0}$
such that the exceptional locus is
$S_{0}$
such that the exceptional locus is
![]() $\ell$
and that
$\ell$
and that
![]() $\ell$
is contracted to an
$\ell$
is contracted to an
![]() $A_{1}$
singularity. Now
$A_{1}$
singularity. Now
![]() $S_{0}$
,
$S_{0}$
,
![]() $S_{1}$
, and
$S_{1}$
, and
![]() $S_{2}$
can be glued together to get a birational contraction morphism
$S_{2}$
can be glued together to get a birational contraction morphism
![]() $q:W\rightarrow S$
onto a complete normal algebraic surface
$q:W\rightarrow S$
onto a complete normal algebraic surface
![]() $S$
, which only contracts
$S$
, which only contracts
![]() $C_{1}^{\prime }$
,
$C_{1}^{\prime }$
,
![]() $C_{2}^{\prime }$
, and
$C_{2}^{\prime }$
, and
![]() $\ell$
.
$\ell$
.
Claim 4.
![]() $\operatorname{Pic}(S)=\{0\}$
holds.
$\operatorname{Pic}(S)=\{0\}$
holds.
Proof of Claim 4.
We take an arbitrary Cartier divisor
![]() $D$
on
$D$
on
![]() $S$
. We put
$S$
. We put
![]() $\overline{D}:=q^{\ast }D$
and
$\overline{D}:=q^{\ast }D$
and
![]() $D^{\dagger }:=p_{\ast }\overline{D}$
. Then we can write
$D^{\dagger }:=p_{\ast }\overline{D}$
. Then we can write
![]() $D^{\dagger }\sim \unicode[STIX]{x1D70B}^{\ast }M+kC_{1}$
for some integer
$D^{\dagger }\sim \unicode[STIX]{x1D70B}^{\ast }M+kC_{1}$
for some integer
![]() $k$
and some Cartier divisor
$k$
and some Cartier divisor
![]() $M$
on
$M$
on
![]() $C$
because
$C$
because
![]() $V$
is
$V$
is
![]() $\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})$
. We note that we can write
$\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})$
. We note that we can write
for some integers
![]() $m_{1}$
and
$m_{1}$
and
![]() $m_{2}$
. By construction,
$m_{2}$
. By construction,
![]() ${\mathcal{O}}_{W}(\overline{D})|_{C_{i}^{\prime }}$
is trivial for
${\mathcal{O}}_{W}(\overline{D})|_{C_{i}^{\prime }}$
is trivial for
![]() $i=1,2$
. Therefore, we have
$i=1,2$
. Therefore, we have
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{C}(M) & \simeq & \displaystyle {\mathcal{O}}_{V}(D^{\dagger })|_{C_{2}}\simeq {\mathcal{O}}_{W}(p^{\ast }D^{\dagger })|_{C_{2}^{\prime }}\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{W}(\overline{D}+m_{1}E_{1}+m_{2}E_{2})|_{C_{2}^{\prime }}\simeq {\mathcal{O}}_{C}(m_{2}P)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{C}(M) & \simeq & \displaystyle {\mathcal{O}}_{V}(D^{\dagger })|_{C_{2}}\simeq {\mathcal{O}}_{W}(p^{\ast }D^{\dagger })|_{C_{2}^{\prime }}\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{W}(\overline{D}+m_{1}E_{1}+m_{2}E_{2})|_{C_{2}^{\prime }}\simeq {\mathcal{O}}_{C}(m_{2}P)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{C}(M-kL) & \simeq & \displaystyle {\mathcal{O}}_{V}(D^{\dagger })|_{C_{1}}\simeq {\mathcal{O}}_{W}(p^{\ast }D^{\dagger })|_{C_{1}^{\prime }}\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{W}(\overline{D}+m_{1}E_{1}+m_{2}E_{2})|_{C_{1}^{\prime }}\simeq {\mathcal{O}}_{C}(m_{1}P).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{C}(M-kL) & \simeq & \displaystyle {\mathcal{O}}_{V}(D^{\dagger })|_{C_{1}}\simeq {\mathcal{O}}_{W}(p^{\ast }D^{\dagger })|_{C_{1}^{\prime }}\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{W}(\overline{D}+m_{1}E_{1}+m_{2}E_{2})|_{C_{1}^{\prime }}\simeq {\mathcal{O}}_{C}(m_{1}P).\nonumber\end{eqnarray}$$
This implies that
![]() ${\mathcal{O}}_{C}(kL)\simeq {\mathcal{O}}_{C}((m_{2}-m_{1})P)$
. Since
${\mathcal{O}}_{C}(kL)\simeq {\mathcal{O}}_{C}((m_{2}-m_{1})P)$
. Since
![]() $\deg L=0$
, we have
$\deg L=0$
, we have
![]() $m_{1}=m_{2}$
. By assumption,
$m_{1}=m_{2}$
. By assumption,
![]() ${\mathcal{L}}={\mathcal{O}}_{C}(L)$
is a nontorsion element of
${\mathcal{L}}={\mathcal{O}}_{C}(L)$
is a nontorsion element of
![]() $\operatorname{Pic}^{0}(C)$
. Thus, we get
$\operatorname{Pic}^{0}(C)$
. Thus, we get
![]() $k=0$
. By construction again, we have
$k=0$
. By construction again, we have
![]() $\overline{D}\cdot \ell =0$
. Therefore,
$\overline{D}\cdot \ell =0$
. Therefore,
holds. Since we have already known that
![]() $m_{1}=m_{2}$
holds, we obtain that
$m_{1}=m_{2}$
holds, we obtain that
![]() $m_{1}=m_{2}=0$
. Thus, we have
$m_{1}=m_{2}=0$
. Thus, we have
![]() $\overline{D}=p^{\ast }D^{\dagger }\sim p^{\ast }\unicode[STIX]{x1D70B}^{\ast }M$
. Since
$\overline{D}=p^{\ast }D^{\dagger }\sim p^{\ast }\unicode[STIX]{x1D70B}^{\ast }M$
. Since
![]() ${\mathcal{O}}_{W}(\overline{D})|_{C_{i}^{\prime }}$
is trivial for
${\mathcal{O}}_{W}(\overline{D})|_{C_{i}^{\prime }}$
is trivial for
![]() $i=1,2$
, we see that
$i=1,2$
, we see that
![]() ${\mathcal{O}}_{C}(M)$
is trivial. Therefore, we obtain
${\mathcal{O}}_{C}(M)$
is trivial. Therefore, we obtain
![]() $\overline{D}\sim 0$
. So we get
$\overline{D}\sim 0$
. So we get
![]() $D\sim 0$
. This means that
$D\sim 0$
. This means that
![]() $\operatorname{Pic}(S)=\{0\}$
.◻
$\operatorname{Pic}(S)=\{0\}$
.◻
By Claim 4, we see that
![]() $S$
is obviously nonprojective. By construction, we can see that
$S$
is obviously nonprojective. By construction, we can see that
![]() $\unicode[STIX]{x1D70B}_{1}(S)=\{1\}$
, that is,
$\unicode[STIX]{x1D70B}_{1}(S)=\{1\}$
, that is,
![]() $S$
is simply connected.
$S$
is simply connected.
From now on, we assume that
![]() $C$
is an elliptic curve. Then
$C$
is an elliptic curve. Then
![]() $S$
has two simple elliptic singularities and one
$S$
has two simple elliptic singularities and one
![]() $A_{1}$
singularity. Moreover,
$A_{1}$
singularity. Moreover,
![]() $S$
is Gorenstein and
$S$
is Gorenstein and
![]() $K_{S}\sim 0$
. We note that
$K_{S}\sim 0$
. We note that
![]() $K_{V}+C_{1}+C_{2}\sim 0$
and
$K_{V}+C_{1}+C_{2}\sim 0$
and
![]() $K_{W}+C_{1}^{\prime }+C_{2}^{\prime }\sim 0$
by construction. We can easily check that
$K_{W}+C_{1}^{\prime }+C_{2}^{\prime }\sim 0$
by construction. We can easily check that
![]() $H^{1}(S,{\mathcal{O}}_{S})=0$
and
$H^{1}(S,{\mathcal{O}}_{S})=0$
and
![]() $H^{2}(S,{\mathcal{O}}_{S})=\mathbb{C}$
by using the Leray spectral sequence. Therefore,
$H^{2}(S,{\mathcal{O}}_{S})=\mathbb{C}$
by using the Leray spectral sequence. Therefore,
![]() $S$
is a complete nonprojective log canonical Calabi–Yau algebraic surface with
$S$
is a complete nonprojective log canonical Calabi–Yau algebraic surface with
![]() $\operatorname{Pic}(S)=\{0\}$
.
$\operatorname{Pic}(S)=\{0\}$
.
From now on, by taking blow-ups of
![]() $S$
in Example 12.3, we construct complete nonprojective algebraic surfaces with a large Picard number.
$S$
in Example 12.3, we construct complete nonprojective algebraic surfaces with a large Picard number.
Example 12.4. Let
![]() $S$
be the surface constructed in Example 12.3, which is birationally equivalent to
$S$
be the surface constructed in Example 12.3, which is birationally equivalent to
![]() $\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})$
. As we saw above,
$\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{L}})$
. As we saw above,
![]() $\operatorname{Pic}(S)=\{0\}$
holds. We take the minimal resolution
$\operatorname{Pic}(S)=\{0\}$
holds. We take the minimal resolution
![]() $\unicode[STIX]{x1D707}:\widetilde{S}\rightarrow S$
of the unique
$\unicode[STIX]{x1D707}:\widetilde{S}\rightarrow S$
of the unique
![]() $A_{1}$
singularity of
$A_{1}$
singularity of
![]() $S$
. Since
$S$
. Since
![]() $S$
is simply connected, so is
$S$
is simply connected, so is
![]() $\widetilde{S}$
. Let
$\widetilde{S}$
. Let
![]() $E$
denote the exceptional curve of
$E$
denote the exceptional curve of
![]() $\unicode[STIX]{x1D707}$
. Of course,
$\unicode[STIX]{x1D707}$
. Of course,
![]() $E$
is the strict transform of
$E$
is the strict transform of
![]() $\ell$
in Example 12.3 and is a
$\ell$
in Example 12.3 and is a
![]() $(-2)$
-curve on
$(-2)$
-curve on
![]() $\widetilde{S}$
.
$\widetilde{S}$
.
Claim 5.
![]() $\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{O}}_{\widetilde{S}}(E)$
holds.
$\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{O}}_{\widetilde{S}}(E)$
holds.
Proof of Claim 5.
By construction, we see that
![]() $E\simeq \mathbb{P}^{1}$
and that
$E\simeq \mathbb{P}^{1}$
and that
![]() $-E$
and
$-E$
and
![]() $-(K_{\widetilde{S}}+E)$
are both
$-(K_{\widetilde{S}}+E)$
are both
![]() $\unicode[STIX]{x1D707}$
-ample. Thus, by Theorem 3.11 (see also Remark 11.4), we have
$\unicode[STIX]{x1D707}$
-ample. Thus, by Theorem 3.11 (see also Remark 11.4), we have
![]() $\operatorname{Pic}(\widetilde{S})\otimes \mathbb{Q}=\mathbb{Q}{\mathcal{O}}_{\widetilde{S}}(E)$
since
$\operatorname{Pic}(\widetilde{S})\otimes \mathbb{Q}=\mathbb{Q}{\mathcal{O}}_{\widetilde{S}}(E)$
since
![]() $\operatorname{Pic}(S)=\{0\}$
. Let
$\operatorname{Pic}(S)=\{0\}$
. Let
![]() ${\mathcal{N}}$
be a torsion element of
${\mathcal{N}}$
be a torsion element of
![]() $\operatorname{Pic}(\widetilde{S})$
. Then we have
$\operatorname{Pic}(\widetilde{S})$
. Then we have
![]() ${\mathcal{N}}\cdot E=0$
. Therefore, by Theorem 3.11 again,
${\mathcal{N}}\cdot E=0$
. Therefore, by Theorem 3.11 again,
![]() ${\mathcal{N}}$
is trivial. This means that
${\mathcal{N}}$
is trivial. This means that
![]() $\operatorname{Pic}(\widetilde{S})$
is torsion-free. Thus, we can write
$\operatorname{Pic}(\widetilde{S})$
is torsion-free. Thus, we can write
![]() $\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{M}}$
for some line bundle
$\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{M}}$
for some line bundle
![]() ${\mathcal{M}}$
on
${\mathcal{M}}$
on
![]() $\widetilde{S}$
. Therefore, there exists some integer
$\widetilde{S}$
. Therefore, there exists some integer
![]() $a$
such that
$a$
such that
![]() ${\mathcal{O}}_{\widetilde{S}}(E)\simeq {\mathcal{M}}^{\otimes a}$
. Since
${\mathcal{O}}_{\widetilde{S}}(E)\simeq {\mathcal{M}}^{\otimes a}$
. Since
![]() $E^{2}=-2$
, we have
$E^{2}=-2$
, we have
![]() $aE\cdot {\mathcal{M}}=-2$
. Note that
$aE\cdot {\mathcal{M}}=-2$
. Note that
![]() $E\cdot {\mathcal{M}}$
is an integer. If
$E\cdot {\mathcal{M}}$
is an integer. If
![]() $a=\pm 2$
, then
$a=\pm 2$
, then
![]() $-2=E^{2}=a^{2}{\mathcal{M}}^{2}=4{\mathcal{M}}^{2}$
. This is a contradiction because
$-2=E^{2}=a^{2}{\mathcal{M}}^{2}=4{\mathcal{M}}^{2}$
. This is a contradiction because
![]() ${\mathcal{M}}^{2}$
is an integer. Thus, we get
${\mathcal{M}}^{2}$
is an integer. Thus, we get
![]() $a=\pm 1$
. This means that
$a=\pm 1$
. This means that
![]() $\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{O}}_{\widetilde{S}}(E)$
.◻
$\operatorname{Pic}(\widetilde{S})=\mathbb{Z}{\mathcal{O}}_{\widetilde{S}}(E)$
.◻
By Claim 5, we have
![]() $N^{1}(\widetilde{S})=\mathbb{R}$
and
$N^{1}(\widetilde{S})=\mathbb{R}$
and
![]() $\overline{\operatorname{NE}}(\widetilde{S})=N_{1}(\widetilde{S})=\mathbb{R}$
. We note that
$\overline{\operatorname{NE}}(\widetilde{S})=N_{1}(\widetilde{S})=\mathbb{R}$
. We note that
![]() $E^{2}=-2$
and that there exists a curve
$E^{2}=-2$
and that there exists a curve
![]() $G$
on
$G$
on
![]() $\widetilde{S}$
such that
$\widetilde{S}$
such that
![]() $G\cdot E>0$
.
$G\cdot E>0$
.
We further assume that
![]() $C$
is an elliptic curve. Then
$C$
is an elliptic curve. Then
![]() $K_{\widetilde{S}}\sim 0$
and
$K_{\widetilde{S}}\sim 0$
and
![]() $\widetilde{S}$
has only two simple elliptic singularities. Therefore,
$\widetilde{S}$
has only two simple elliptic singularities. Therefore,
![]() $\widetilde{S}$
is a complete nonprojective log canonical Calabi–Yau algebraic surface with
$\widetilde{S}$
is a complete nonprojective log canonical Calabi–Yau algebraic surface with
![]() $\overline{\operatorname{NE}}(\widetilde{S})=\mathbb{R}$
.
$\overline{\operatorname{NE}}(\widetilde{S})=\mathbb{R}$
.
Example 12.5. Let
![]() $\widetilde{S}$
be the surface constructed in Example 12.4. We take finitely many smooth points
$\widetilde{S}$
be the surface constructed in Example 12.4. We take finitely many smooth points
![]() $Q_{1},Q_{2},\ldots ,Q_{\unicode[STIX]{x1D70C}-1}$
of
$Q_{1},Q_{2},\ldots ,Q_{\unicode[STIX]{x1D70C}-1}$
of
![]() $\widetilde{S}$
with
$\widetilde{S}$
with
![]() $\unicode[STIX]{x1D70C}\geqslant 2$
such that
$\unicode[STIX]{x1D70C}\geqslant 2$
such that
![]() $Q_{i}\neq Q_{j}$
for
$Q_{i}\neq Q_{j}$
for
![]() $i\neq j$
and
$i\neq j$
and
![]() $Q_{i}\not \in E$
for every
$Q_{i}\not \in E$
for every
![]() $i$
. We blow up
$i$
. We blow up
![]() $Q_{1},Q_{2},\ldots ,Q_{\unicode[STIX]{x1D70C}-1}$
to get
$Q_{1},Q_{2},\ldots ,Q_{\unicode[STIX]{x1D70C}-1}$
to get
![]() $\unicode[STIX]{x1D70E}:\overline{S}\rightarrow \widetilde{S}$
. Let
$\unicode[STIX]{x1D70E}:\overline{S}\rightarrow \widetilde{S}$
. Let
![]() $B_{i}$
denote the
$B_{i}$
denote the
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $\overline{S}$
with
$\overline{S}$
with
![]() $\unicode[STIX]{x1D70E}(B_{i})=Q_{i}$
for every
$\unicode[STIX]{x1D70E}(B_{i})=Q_{i}$
for every
![]() $i$
. Then, by Theorem 3.11 (see also Remark 11.4), we can easily check that
$i$
. Then, by Theorem 3.11 (see also Remark 11.4), we can easily check that
Claim 6.
![]() $\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
holds.
$\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
holds.
Proof of Claim 6.
Let
![]() $D$
be a nef
$D$
be a nef
![]() $\mathbb{R}$
-Cartier
$\mathbb{R}$
-Cartier
![]() $\mathbb{R}$
-divisor on
$\mathbb{R}$
-divisor on
![]() $\overline{S}$
. It is sufficient to prove that
$\overline{S}$
. It is sufficient to prove that
![]() $D$
is numerically trivial. By the above description of
$D$
is numerically trivial. By the above description of
![]() $\operatorname{Pic}(\overline{S})$
, we can assume that
$\operatorname{Pic}(\overline{S})$
, we can assume that
![]() $D=b_{0}\unicode[STIX]{x1D70E}^{\ast }E+\sum _{i=1}^{\unicode[STIX]{x1D70C}-1}b_{i}B_{i}$
, where
$D=b_{0}\unicode[STIX]{x1D70E}^{\ast }E+\sum _{i=1}^{\unicode[STIX]{x1D70C}-1}b_{i}B_{i}$
, where
![]() $b_{i}\in \mathbb{R}$
for every
$b_{i}\in \mathbb{R}$
for every
![]() $i$
. Since
$i$
. Since
![]() $D\cdot B_{i}\geqslant 0$
for every
$D\cdot B_{i}\geqslant 0$
for every
![]() $i$
and
$i$
and
![]() $D\cdot \unicode[STIX]{x1D70E}^{\ast }E\geqslant 0$
,
$D\cdot \unicode[STIX]{x1D70E}^{\ast }E\geqslant 0$
,
![]() $b_{i}\leqslant 0$
holds for every
$b_{i}\leqslant 0$
holds for every
![]() $i$
. We assume that
$i$
. We assume that
![]() $D\neq 0$
. Then we can take an irreducible curve
$D\neq 0$
. Then we can take an irreducible curve
![]() $G$
on
$G$
on
![]() $\overline{S}$
such that
$\overline{S}$
such that
![]() $G\not \subset \operatorname{Supp}D$
and that
$G\not \subset \operatorname{Supp}D$
and that
![]() $G\cap \operatorname{Supp}D\neq \emptyset$
. This is because the smooth locus of
$G\cap \operatorname{Supp}D\neq \emptyset$
. This is because the smooth locus of
![]() $\overline{S}$
is a quasi-projective open subset of
$\overline{S}$
is a quasi-projective open subset of
![]() $\overline{S}$
and contains
$\overline{S}$
and contains
![]() $\unicode[STIX]{x1D70E}^{\ast }E$
and
$\unicode[STIX]{x1D70E}^{\ast }E$
and
![]() $B_{i}$
for every
$B_{i}$
for every
![]() $i$
. Thus we get
$i$
. Thus we get
![]() $D\cdot G<0$
. This is a contradiction. This means that
$D\cdot G<0$
. This is a contradiction. This means that
![]() $D=0$
. Hence we have
$D=0$
. Hence we have
![]() $\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
.◻
$\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
.◻
If
![]() $C$
is an elliptic curve, then
$C$
is an elliptic curve, then
![]() $\overline{S}$
is a complete nonprojective log canonical algebraic surface with
$\overline{S}$
is a complete nonprojective log canonical algebraic surface with
![]() $\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
. By construction, we see that
$\overline{\operatorname{NE}}(\overline{S})=N_{1}(\overline{S})=\mathbb{R}^{\unicode[STIX]{x1D70C}}$
. By construction, we see that
![]() $K_{\overline{S}}=\sum _{i=1}^{\unicode[STIX]{x1D70C}-1}B_{i}$
. We can apply the minimal model program established in Theorem 1.5 to a complete nonprojective log canonical algebraic surface
$K_{\overline{S}}=\sum _{i=1}^{\unicode[STIX]{x1D70C}-1}B_{i}$
. We can apply the minimal model program established in Theorem 1.5 to a complete nonprojective log canonical algebraic surface
![]() $\overline{S}$
. Then every
$\overline{S}$
. Then every
![]() $B_{i}$
is contracted to a smooth point and we finally get a good minimal model
$B_{i}$
is contracted to a smooth point and we finally get a good minimal model
![]() $\widetilde{S}$
, which is a surface with
$\widetilde{S}$
, which is a surface with
![]() $K_{\widetilde{S}}\sim 0$
constructed in Example 12.4.
$K_{\widetilde{S}}\sim 0$
constructed in Example 12.4.
The following commutative diagram may help the reader understand the constructions in Examples 12.3–12.5:

The reader can find various examples of complete nonprojective toric threefolds
![]() $X$
with
$X$
with
![]() $\operatorname{Pic}(X)=\{0\}$
,
$\operatorname{Pic}(X)=\{0\}$
,
![]() $\overline{\operatorname{NE}}(X)=\mathbb{R}_{{\geqslant}0}$
, or
$\overline{\operatorname{NE}}(X)=\mathbb{R}_{{\geqslant}0}$
, or
![]() $\overline{\operatorname{NE}}(X)=N_{1}(X)$
in [Reference FujinoFn1] and [Reference Fujino and PayneFP].
$\overline{\operatorname{NE}}(X)=N_{1}(X)$
in [Reference FujinoFn1] and [Reference Fujino and PayneFP].
Finally, we make a remark on complete nonprojective algebraic surfaces defined over an algebraically closed field
![]() $k$
with
$k$
with
![]() $k\neq \mathbb{C}$
.
$k\neq \mathbb{C}$
.
Remark 12.6. We note that every complete algebraic surface defined over
![]() $\overline{\mathbb{F}}_{p}$
is always
$\overline{\mathbb{F}}_{p}$
is always
![]() $\mathbb{Q}$
-factorial (see [Reference TanakaT, Theorem 4.5]). So it automatically becomes projective (see [Reference FujinoFn4, Lemma 2.2]). By the following lemma (see Lemma 12.7), the constructions in this section and Kollár’s construction in [Reference KollárK1, Aside 3.46] can work for algebraic surfaces defined over an algebraically closed field
$\mathbb{Q}$
-factorial (see [Reference TanakaT, Theorem 4.5]). So it automatically becomes projective (see [Reference FujinoFn4, Lemma 2.2]). By the following lemma (see Lemma 12.7), the constructions in this section and Kollár’s construction in [Reference KollárK1, Aside 3.46] can work for algebraic surfaces defined over an algebraically closed field
![]() $k$
such that
$k$
such that
![]() $k\neq \overline{\mathbb{F}}_{p}$
for every prime number
$k\neq \overline{\mathbb{F}}_{p}$
for every prime number
![]() $p$
with some suitable modifications. We note that Theorem 3.11 holds true for algebraic surfaces defined over any algebraically closed field (see Remark 11.4). Thus, we can construct complete nonprojective algebraic surfaces over an algebraically closed field
$p$
with some suitable modifications. We note that Theorem 3.11 holds true for algebraic surfaces defined over any algebraically closed field (see Remark 11.4). Thus, we can construct complete nonprojective algebraic surfaces over an algebraically closed field
![]() $k$
such that
$k$
such that
![]() $k\neq \overline{\mathbb{F}}_{p}$
for every prime number
$k\neq \overline{\mathbb{F}}_{p}$
for every prime number
![]() $p$
.
$p$
.
Lemma 12.7. Let
![]() $C$
be a smooth projective curve defined over an algebraically closed field
$C$
be a smooth projective curve defined over an algebraically closed field
![]() $k$
whose genus
$k$
whose genus
![]() $g(C)$
is positive. Let
$g(C)$
is positive. Let
![]() $P$
be an arbitrary closed point of
$P$
be an arbitrary closed point of
![]() $C$
. Assume that
$C$
. Assume that
![]() $k\neq \overline{\mathbb{F}}_{p}$
for every prime number
$k\neq \overline{\mathbb{F}}_{p}$
for every prime number
![]() $p$
. Then there exists
$p$
. Then there exists
![]() $Q\in C$
such that
$Q\in C$
such that
![]() ${\mathcal{O}}_{C}(Q-P)$
is a nontorsion element of
${\mathcal{O}}_{C}(Q-P)$
is a nontorsion element of
![]() $\operatorname{Pic}^{0}(C)$
.
$\operatorname{Pic}^{0}(C)$
.
Proof. By
![]() $g(C)\geqslant 1$
and
$g(C)\geqslant 1$
and
![]() $k\neq \overline{\mathbb{F}}_{p}$
, we can take a nontorsion element
$k\neq \overline{\mathbb{F}}_{p}$
, we can take a nontorsion element
![]() ${\mathcal{L}}$
of
${\mathcal{L}}$
of
![]() $\operatorname{Pic}^{0}(C)$
(see [Reference TanakaT, Fact 2.3]). We take a large positive integer
$\operatorname{Pic}^{0}(C)$
(see [Reference TanakaT, Fact 2.3]). We take a large positive integer
![]() $m$
. Then
$m$
. Then
![]() ${\mathcal{L}}\otimes {\mathcal{O}}_{C}(mP)$
is very ample. We consider a general member
${\mathcal{L}}\otimes {\mathcal{O}}_{C}(mP)$
is very ample. We consider a general member
![]() $Q_{1}+\cdots +Q_{m}$
of
$Q_{1}+\cdots +Q_{m}$
of
![]() $|{\mathcal{L}}\otimes {\mathcal{O}}_{C}(mP)|$
. Then we have
$|{\mathcal{L}}\otimes {\mathcal{O}}_{C}(mP)|$
. Then we have
![]() ${\mathcal{L}}\simeq {\mathcal{O}}_{C}((Q_{1}-P)+\cdots +(Q_{m}-P))$
. Therefore, there exists some
${\mathcal{L}}\simeq {\mathcal{O}}_{C}((Q_{1}-P)+\cdots +(Q_{m}-P))$
. Therefore, there exists some
![]() $i_{0}$
such that
$i_{0}$
such that
![]() ${\mathcal{O}}_{C}(Q_{i_{0}}-P)$
is a nontorsion element of
${\mathcal{O}}_{C}(Q_{i_{0}}-P)$
is a nontorsion element of
![]() $\operatorname{Pic}^{0}(C)$
.◻
$\operatorname{Pic}^{0}(C)$
.◻
Acknowledgments
The author would like to thank Kenta Hashizume, Haidong Liu, and Hiromu Tanaka for very useful comments and for pointing out some mistakes. He would also like to thank Kento Fujita very much for useful discussions and advice, and for allowing him to use his ideas on complete nonprojective algebraic surfaces in Section 12. Finally, he thanks Seiko Hashimoto for her help and the referees for many comments.