Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-23T09:45:38.350Z Has data issue: false hasContentIssue false
  • English
  • Français

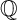${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION

Part of: Special varieties Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  20 January 2025

LIANA HEUBERGER Open the ORCID record for LIANA HEUBERGER [Opens in a new window]
LIANA HEUBERGER*
Affiliation:
Institut de Mathématiques de Marseille 3 Place Victor Hugo 13331 Marseille Cedex 3 France
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct families of non-toric 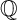${\mathbb {Q}}$-factorial terminal Fano (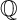${\mathbb {Q}}$-Fano) threefolds of codimension 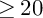$\geq 20$ corresponding to 54 mutation classes of rigid maximally mutable Laurent polynomials. From the point of view of mirror symmetry, they are the highest codimension (non-toric) 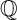${\mathbb {Q}}$-Fano varieties for which we can currently establish the Fano/Landau–Ginzburg correspondence. We construct 46 additional 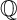${\mathbb {Q}}$-Fano threefolds with codimensions of new examples ranging between 19 and 5. Some of these varieties are presented as toric complete intersections, and others as Pfaffian varieties.

Keywords

Fano varietiesmirror symmetrytoric degenerations

MSC classification

Primary: 14J45: Fano varieties 14M25: Toric varieties, Newton polyhedra
Secondary: 14J33: Mirror symmetry
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 47
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhtar, M., Coates, T., Galking, S. and Kasprzyk, A. “Minkowski polynomials and mutations” This is published online in SIGMA 8, Special Issue Mirror Symmetry and Related Topics, 2012.CrossRefGoogle Scholar
Akhtar, M. and Kasprzyk, A., Singularity content. Preprint, 2014, arXiv:1401.5458.Google Scholar
Altinok, S., Brown, G. and Reid, M., “Fano 3-folds, K3 surfaces and graded rings” in Topology and Geometry: Commemorating SISTAG, Contemporary Mathematics, Vol. 314, American Mathematical Society, Providence, RI, 2002, 25–53.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system I: The user language , J. Symbolic Comput. 24 (1997), no. 3, 235–265.CrossRefGoogle Scholar
Brown, G. and Kasprzyk, A., Kawamata boundedness for Fano threefolds and the Graded Ring Database, Preprint, 2022, arXiv:2201.07178.Google Scholar
Brown, G. and Kasprzyk, A. M., The graded ring database. Database of possible Hilbert series of $\mathbb{Q}$ -factorial terminal Fano $3$ -folds, online. http://grdb.co.uk/forms/fano3.Google Scholar
Brown, G. and Kasprzyk, A. M., The Graded Ring Database. Database of toric canonical $3$ -folds, online. http://grdb.co.uk/forms/toricf3c.Google Scholar
Brown, G. and Kasprzyk, A. M., The Fano 3-fold database, Zenodo, 2022. https://doi.org/10.5281/zenodo.5820338.CrossRefGoogle Scholar
Buchsbaum, D. A. and Eisenbud, D., Algebra structures for finite free resolutions, and some structure theorems for ideals of codimension 3 , Amer. J. Math. 99 (1977), no. 3, 447–485.CrossRefGoogle Scholar
Coates, T., Corti, A., Galkin, S., Golyshev, V. and Kasprzyk, A., Mirror symmetry and Fano manifolds , Eur. Congr. Math. Kraków (2012), 285–300.Google Scholar
Coates, T., Corti, A., Galkin, S. and Kasprzyk, A. Quantum periods for 3–dimensional Fano manifolds , Geom. Topol. 20) (2016), no. 1, 103–256.CrossRefGoogle Scholar
Coates, T., Corti, A., Iritani, H. and Tseng, H.-H., A mirror theorem for toric stacks , Compos. Math. 151 (2015), no. 10, 1878–1912.CrossRefGoogle Scholar
Coates, T. and Kasprzyk, A. Fanosearch software library, 2022. https://bitbucket.org/fanosearch/magma-core, commit 1ec4c69.Google Scholar
Coates, T., Kasprzyk, A. and Pitton, G. Certain rigid maximally mutable Laurent polynomials in three variables , Zenodo. (2022) https://doi.org/10.5281/zenodo.6636221.Google Scholar
Coates, T., Kasprzyk, A. and Prince, T., Laurent inversion , Pure Appl. Math. Quart. 15 (2019), 1135–1179.CrossRefGoogle Scholar
Coates, T., Kasprzyk, A. M, Pitton, G. and Tveiten, K. Maximally mutable Laurent polynomials , Proc. Royal Soc. A: Math., Phys. Eng. Sci. 477 (2021), no. 2254.Google Scholar
Corti, A., Filip, M. and Petracci, A. Mirror symmetry and smoothing Gorenstein toric affine 3-folds , Facets of Algebraic Geometry. To appear (2020). arXiv:2006.16885.Google Scholar
Corti, A. and Heuberger, L. Del Pezzo surfaces with 1/3(1,1) points , Manuscripta Math. 153 (2016), 71–118.CrossRefGoogle Scholar
Coughlan, S. and Ducat, T. Constructing Fano 3-folds from cluster varieties of rank 2 , Compos. Math. 156 (2020), no. 9, 1873–1914.CrossRefGoogle Scholar
Doran, C. F. and Harder, A. Toric degenerations and Laurent polynomials related to Givental’s Landau–Ginzburg Models , Can. J. Math. 68 (2016), no. 4, 784–815.CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E. Macaulay2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Harris, J. and Tu, L. W. On symmetric and skew-symmetric determinantal varieties , Topology. 23 (1984), no. 1, 71–84.CrossRefGoogle Scholar
Ilten, N. O. Mutations of Laurent polynomials and flat families with toric fibers. This is published online in SIGMA 8, Special Issue Mirror Symmetry and Related Topics, 2012.CrossRefGoogle Scholar
Kasprzyk, A. Canonical toric Fano threefolds , Can. J. Math. 62 (2010), no. 6, 1293–1309.CrossRefGoogle Scholar
Kasprzyk, A., Akhtar, M., Coates, T., Corti, A., Heuberger, L., Oneto, A., Petracci, A., Prince, T. and Tveiten, K. Mirror symmetry and the classification of orbifold del Pezzo surfaces , Proc. Amer. Math. Soc. 144 (2016), 513–527.Google Scholar
Kasprzyk, A. M. The classification of toric canonical Fano 3-folds , Zenodo, (2010b). https://doi.org/10.5281/zenodo.5866330.Google Scholar
Petracci, A. On deformations of toric Fano varieties , Interact. Lattice Polytopes, To appear. (2019a). arXiv:1912.01538.Google Scholar
Petracci, A. Some examples of non-smoothable Gorenstein Fano toric threefolds , Mathematische Zeitschrift. 295 (2019b), nos. 1–2, 751–760.CrossRefGoogle Scholar
Petracci, A. Homogeneous deformations of toric pairs , Manuscr. Math. 166 (2020), nos. 1–2, 37–72.CrossRefGoogle Scholar
Prince, T. Cracked polytopes and Fano toric complete intersections , Manuscr. Math. 163 (2020), no. 1-2, 165–183.CrossRefGoogle Scholar
Prince, T. From cracked polytopes to Fano threefolds , Manuscr. Math. 164 (2021), no. 1-2, 267–320.CrossRefGoogle Scholar
Przyjalkowski, V. On Landau-Ginzburg models for Fano varieties , Commun. Number Theory Phys. 1 (2008), no. 4, 713–728.CrossRefGoogle Scholar
Suzuki, K. On Fano indices of $\mathbb{Q}$ -Fano 3-folds , Manuscr. Math. 114 (2004), 229–246.CrossRefGoogle Scholar
Suzuki, K. and Brown, G. Computing certain Fano 3-folds , Japan J. Indust. Appl. Math. 24 (2007), no. 3, 241–250.Google Scholar
Suzuki, K. and Brown, G. Fano 3-folds with divisible anticanonical class , Manuscripta Math. 123 (2007), no. 1, 37–51.Google Scholar
Takagi, H. On classification of $\mathbb{Q}$ -Fano 3-folds of Gorenstein index 2, I and II . Nagoya Math. J. 167 (2002), nos. 117–155, 157–216.CrossRefGoogle Scholar
Wang, J., A mirror theorem for Gromov–Witten theory without convexity, Preprint, 2019, arXiv:1910.14440.Google Scholar