Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T22:57:59.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Localized Morrey-Campanato spaces on metric measure spaces and applications to Schrüdinger operators

Published online by Cambridge University Press:  11 January 2016

Dachun Yang ,
Dongyong Yang  and
Yuan Zhou
Dachun Yang
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s, Republic of [email protected]
Dongyong Yang
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s, Republic of [email protected]
Yuan Zhou
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s, Republic of [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

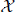Let be a space of homogeneous type in the sense of Coifman and Weiss, and let 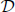be a collection of balls in 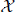. The authors introduce the localized atomic Hardy space 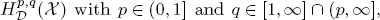the localized Morrey-Campanato space 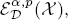and the localized Morrey-Campanato-BLO (bounded lower oscillation) space 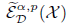with α ∊ ℝ and p ∊ (0, ∞) , and they establish their basic properties, including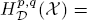 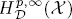and several equivalent characterizations for 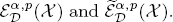In particular, the authors prove that when α > 0 and p ∊ [1, ∞), then 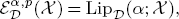and when p ∈(0,1], then the dual space of 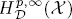is 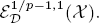Let ρ be an admissible function modeled on the known auxiliary function determined by the Schrödinger operator. 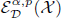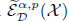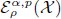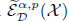Denote the spaces and , respectively, by and when 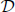is determined by ρ. The authors then obtain the boundedness from 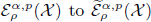of the radial and the Poisson semigroup maximal functions and the Littlewood-Paley g-function, which are defined via kernels modeled on the semigroup generated by the Schrödinger operator. These results apply in a wide range of settings, for instance, the Schrödinger operator or the degenerate Schrödinger operator on ℝd, or the sub-Laplace Schrödinger operator on Heisenberg groups or connected and simply connected nilpotent Lie groups.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 198 , June 2010 , pp. 77 - 119
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2010

References

[1] Campanato, S., Proprietà di hölderianità di alcune classi di funzioni, Ann. Sc. Norm. Super. Pisa 17 (1963), 175–188.Google Scholar
[2] Coifman, R. R. and Rochberg, R., Another characterization of BMO, Proc. Amer. Math. Soc. 79 (1980), 249–254.CrossRefGoogle Scholar
[3] Coifman, R. R. and Weiss, G., Analyse Harmonique Non-commutative sur Certains Espaces Homogènes, Lecture Notes in Math. 242, Springer, Berlin, 1971.Google Scholar
[4] Coifman, R. R. and Weiss, G., Extensions of Hardy spaces and their use in analysis, Bull. Amer. Math. Soc. 83 (1977), 569–645.CrossRefGoogle Scholar
[5] Duong, X. T., Xiao, J., and Yan, L., Old and new Morrey spaces with heat kernel bounds, J. Fourier Anal. Appl. 13 (2007), 87–111.CrossRefGoogle Scholar
[6] Dziubanski, J., Note on H1 spaces related to degenerate Schrödinger operators, Illinois J. Math. 49 (2005), 1271–1297.CrossRefGoogle Scholar
[7] Dziubanski, J., Garrigös, G., Martônez, T., Torrea, J. L., and Zienkiewicz, J., BMO spaces related to Schrödinger operators with potentials satisfying a reverse Holder inequality, Math. Z. 249 (2005), 329–356.CrossRefGoogle Scholar
[8] Dziubanski, J. and Zienkiewicz, J., Hardy space H1 associated to Schrödinger operator with potential satisfying reverse Holder inequality, Rev. Mat. Iberoam. 15 (1999), 279–296.CrossRefGoogle Scholar
[9] Dziubanski, J. and Zienkiewicz, J., Hp spaces associated with Schrödinger operators with potentials from reverse Holder classes, Colloq. Math. 98 (2003), 5–38.CrossRefGoogle Scholar
[10] Fefferman, C., The uncertainty principle, Bull. Amer. Math. Soc. (N.S.) 9 (1983), 129–206.CrossRefGoogle Scholar
[11] Goldberg, D., A local version of real Hardy spaces, Duke Math. J. 46 (1979), 27–42.CrossRefGoogle Scholar
[12] Han, Y., Müller, D., and Yang, D., A theory of Besov and Triebel-Lizorkin spaces on metric measure spaces modeled on Carnot-Carathéodory spaces, Abstr. Appl. Anal. 2008, no. 89 3409.Google Scholar
[13] Hebisch, W. and Saloff-Coste, L., On the relation between elliptic and parabolic Harnack inequalities, Ann. Inst. Fourier (Grenoble) 51 (2001), 1437–1481.CrossRefGoogle Scholar
[14] Hu, G., Meng, Y., and Yang, D., Estimates for Marcinkiewicz integrals in BMO and Campanato spaces, Glasg. Math. J. 49 (2007), 167–187.CrossRefGoogle Scholar
[15] Hu, G., Yang, D., and Yang, D., h1, bmo, blo and Littlewood-Paley g-functions with non-doubling measures, Rev. Mat. Iberoam. 25 (2009), 595–667.CrossRefGoogle Scholar
[16] Huang, J. and Liu, H., Area integrals associated to Schrödinger operators, preprint.Google Scholar
[17] Lemarié-Rieusset, P. G., The Navier-Stokes equations in the critical Morrey-Campanato space, Rev. Mat. Iberoam. 23 (2007), 897–930.CrossRefGoogle Scholar
[18] Li, H., Estimations Lp des opérateurs de Schrödinger sur les groupes nilpotents, J. Funct. Anal. 161 (1999), 152–218.CrossRefGoogle Scholar
[19] Lin, C. and Liu, H., The BMO-type space BMOc associated with Schrödinger operatorson the Heisenberg group, preprint.Google Scholar
[20] Macías, R. A. and Segovia, C., Lipschitz functions on spaces of homogeneous type, Adv. Math. 33 (1979), 257–270.CrossRefGoogle Scholar
[21] Nagel, A., Stein, E. M., and Wainger, S., Balls and metrics defined by vector fields I. Basic properties, Acta Math. 155 (1985), 103–147.CrossRefGoogle Scholar
[22] Nakai, E., The Campanato, Morrey and Holder spaces on spaces of homogeneous type, Studia Math. 176 (2006), 1–19.Google Scholar
[23] Nakai, E., Orlicz-Morrey spaces and the Hardy-Littlewood maximal function, Studia Math. 188 (2008), 193–221.CrossRefGoogle Scholar
[24] Peetre, J., On the theory of £ptλ spaces, J. Funct. Anal. 4 (1969), 71–87.CrossRefGoogle Scholar
[25] Shen, Z., Lp estimates for Schrödinger operators with certain potentials, Ann. Inst. Fourier (Grenoble) 45 (1995), 513–546.CrossRefGoogle Scholar
[26] Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton University Press, Princeton, 1993.Google Scholar
[27] Strömberg, J.-O. and Torchinsky, A., Weighted Hardy Spaces, Lecture Notes in Math. 1381, Springer, Berlin, 1989.Google Scholar
[28] Taibleson, M. H. and Weiss, G., “The molecular characterization of certain Hardy spaces,” in Representation Theorems for Hardy Spaces, Astérisque 77, Soc. Math. France, Paris, 1980, 67–149.Google Scholar
[29] Triebel, H., Theory of Function Spaces, Vol. II, Birkhäuser, Basel, 1992.Google Scholar
[30] Varopoulos, N. T., Analysis on Lie groups, J. Funct. Anal. 76 (1988), 346–410.Google Scholar
[31] Varopoulos, N. T., Saloff-Coste, L., and Coulhon, T., Analysis and Geometry on Groups, Cambridge University Press, Cambridge, 1992.Google Scholar
[32] Yang, D., Yang, D., and Zhou, Y., Localized BMO and BLO spaces on RD-spaces and applications to Schrödinger operators, Commun. Pure Appl. Anal. 9 (2010), 779–812.CrossRefGoogle Scholar
[33] Yang, D. and Zhou, Y., Localized Hardy spaces H1related to admissible functions on RD-spaces and applications to Schröodinger operators, to appear in Trans. Amer. Math. Soc.Google Scholar
[34] Zhong, J., The Sobolev estimates for some Schrödinger type operators, Math. Sci. Res. Hot-Line 3 (1999), 1–48.Google Scholar