Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bakun, V. V.
2000.
On generalized local time for the process of brownian motion.
Ukrainian Mathematical Journal,
Vol. 52,
Issue. 2,
p.
173.
Дороговцев, Андрей Анатольевич
Dorogovtsev, Andrei Anatol'evich
Бакунин, Вадим Васильевич
and
Bakunin, Vadim Vasilyevich
2003.
Случайные отображения и обобщенные аддитивные функционалы от винеровского процесса.
Теория вероятностей и ее применения,
Vol. 48,
Issue. 1,
p.
43.
Dorogovtsev, A. A.
and
Bakun, V. V.
2004.
Random Mappings and a Generalized Additive Functional of a Wiener Process.
Theory of Probability & Its Applications,
Vol. 48,
Issue. 1,
p.
63.
Hu, Yaozhong
and
Nualart, David
2005.
Renormalized self-intersection local time for fractional Brownian motion.
The Annals of Probability,
Vol. 33,
Issue. 3,
Hu, Yaozhong
Nualart, David
and
Song, Jian
2008.
Integral representation of renormalized self-intersection local times.
Journal of Functional Analysis,
Vol. 255,
Issue. 9,
p.
2507.
Liu, Junfeng
Peng, Zhihang
Tang, Donglei
Cang, Yuquan
and
El-Sayed, Ahmed
2012.
On the Self‐Intersection Local Time of Subfractional Brownian Motion.
Abstract and Applied Analysis,
Vol. 2012,
Issue. 1,
Bock, Wolfgang
Fattler, Torben
and
Streit, Ludwig
2017.
Stochastic Quantization for the Fractional Edwards Measure.
Acta Applicandae Mathematicae,
Vol. 151,
Issue. 1,
p.
81.
Evans, Steven
Pitman, Jim
and
Tang, Wenpin
2017.
The spans in Brownian motion.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 53,
Issue. 3,
Chen, Zhenlong
Sang, Liheng
and
Hao, Xiaozhen
2018.
Renormalized self-intersection local time of bifractional Brownian motion.
Journal of Inequalities and Applications,
Vol. 2018,
Issue. 1,
Bock, Wolfgang
da Silva, José Luís
and
Fattler, Torben
2018.
Analysis of Stochastic Quantization for the Fractional Edwards Measure.
Reports on Mathematical Physics,
Vol. 82,
Issue. 2,
p.
187.
Bock, Wolfgang
da Silva, Jose Luis
and
Suryawan, Herry Pribawanto
2020.
Self-intersection local times for multifractional Brownian motion in higher dimensions: A white noise approach.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 23,
Issue. 01,
p.
2050007.
Kuang, Nenghui
and
Liu, Bingquan
2022.
Renormalized self-intersection local time for sub-bifractional Brownian motion.
Filomat,
Vol. 36,
Issue. 12,
p.
4023.
Sang, Liheng
and
Chen, Zhenlong
2023.
Existence and Smoothness of Local Time and Self-intersection Local Time for Spherical Gaussian Random Fields.
Frontiers of Mathematics,
Vol. 18,
Issue. 3,
p.
591.
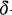 -function and precise computation we get a deep insight into the problem. In the section 1 multiple Wiener integrals with respect to multidimensional Brownian motion and chaotic representations for square-integrable Wiener functionals are given. They are indispensable, but seem not to be formulated clearly and correctly before. The useful concepts and results of white noise analysis are illustrated in the section 2. Section 3 is the main part of the paper. The applications to local times are introduced in the section 4 briefly.
-function and precise computation we get a deep insight into the problem. In the section 1 multiple Wiener integrals with respect to multidimensional Brownian motion and chaotic representations for square-integrable Wiener functionals are given. They are indispensable, but seem not to be formulated clearly and correctly before. The useful concepts and results of white noise analysis are illustrated in the section 2. Section 3 is the main part of the paper. The applications to local times are introduced in the section 4 briefly.

