Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pellegrini, Clément
2010.
Markov chains approximation of jump–diffusion stochastic master equations.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 46,
Issue. 4,
Jacod, Jean
2018.
Limit of Random Measures Associated with the Increments of a Brownian Semimartingale.
Journal of Financial Econometrics,
Vol. 16,
Issue. 4,
p.
526.



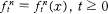 is a stochastic process and
is a stochastic process and 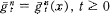 is a deterministic function, both of which take values in the space of vector fields. The case where
is a deterministic function, both of which take values in the space of vector fields. The case where 