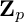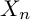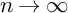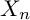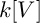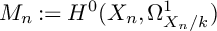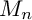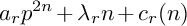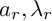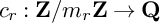IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p

Abstract

We investigate a novel geometric Iwasawa theory for ${\mathbf Z}_p$ -extensions of function fields over a perfect field k of characteristic $p>0$ by replacing the usual study of p-torsion in class groups with the study of p-torsion class group schemes. That is, if $\cdots \to X_2 \to X_1 \to X_0$ is the tower of curves over k associated with a ${\mathbf Z}_p$ -extension of function fields totally ramified over a finite nonempty set of places, we investigate the growth of the p-torsion group scheme in the Jacobian of $X_n$ as $n\rightarrow \infty $ . By Dieudonné theory, this amounts to studying the first de Rham cohomology groups of $X_n$ equipped with natural actions of Frobenius and of the Cartier operator V. We formulate and test a number of conjectures which predict striking regularity in the $k[V]$ -module structure of the space $M_n:=H^0(X_n, \Omega ^1_{X_n/k})$ of global regular differential forms as $n\rightarrow \infty .$ For example, for each tower in a basic class of ${\mathbf Z}_p$ -towers, we conjecture that the dimension of the kernel of $V^r$ on $M_n$ is given by $a_r p^{2n} + \lambda _r n + c_r(n)$ for all n sufficiently large, where $a_r, \lambda _r$ are rational constants and $c_r : {\mathbf Z}/m_r {\mathbf Z} \to {\mathbf Q}$ is a periodic function, depending on r and the tower. To provide evidence for these conjectures, we collect extensive experimental data based on new and more efficient algorithms for working with differentials on ${\mathbf Z}_p$ -towers of curves, and we prove our conjectures in the case $p=2$ and $r=1$ .

1 Introduction

1.1 Geometric Iwasawa theory

Fix a perfect field k of characteristic $p>0$ , and an algebraic function field K in one variable over k. Let $L/K$ be a Galois extension with $\Gamma :=\operatorname {\mathrm {Gal}}(L/K)\simeq {\mathbf Z}_p$ , the group of p-adic integers. We suppose that $L/K$ is unramified outside a finite set of places S of K (which are trivial on k) and totally ramified at every place in S. ¹ Let $\Gamma _n:=p^n{\mathbf Z}_p$ , and write $K_n = L^{\Gamma _n}$ for the fixed field of $\Gamma _n$ .

In the spirit of classical Iwasawa theory, we seek to understand the growth of the p-primary part of the class group of $K_n$ as n grows. When L is the constant ${\mathbf Z}_p$ -extension of K, the regular growth of the class groups of $K_n$ was indeed Iwasawa’s primary motivation for the eponymous theory he initiated for number fields [I]. When k is algebraically closed in L—which we assume henceforth—the growth of the class groups of $K_n$ with k finite has been studied by Mazur and Wiles [MW] and Crew [C2, §3] (for S nonempty) and by Gold and Kisilevsky [GK]. These works analyze the physical class group $\operatorname {\mathrm {Cl}}_{K_n}$ of degree zero divisor classes defined over k modulo linear equivalence, and prove—in perfect analogy with the number field setting—that when k is a finite field, the Iwasawa module $\varprojlim _n \operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }]$ is finitely generated and torsion over $\Lambda :={\mathbf Z}_p[\![\Gamma ]\!]$ , with no finite submodules. The celebrated growth formula $\# \operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }] = p^{n\lambda +p^n\mu +\nu }$ for $n\gg 0$ follows.

In this function field setting, however, there is another, far more interesting motivic interpretation of “class group” provided by the Jacobian of the associated algebraic curve. Writing $X_n$ for the unique smooth, projective, and geometrically connected curve over k with function field $K_n$ (with $K_0 = K$ corresponding to $X_0$ ), we obtain a ${\mathbf Z}_p$ -tower of curves

$$\begin{align*}\mathcal{T} : \cdots \to X_n \to \cdots \to X_2 \to X_1 \to X_0 \end{align*}$$

with $X_n\rightarrow X_0$ a branched ${\mathbf Z}/p^n{\mathbf Z}$ -cover, unramified outside a finite set of points S of $X_0$ and totally ramified over every point of S. For each n, the Jacobian $J_{X_n}:=\operatorname {\mathrm {Pic}}^0_{X_n/k}$ represents the functor of equivalence classes of degree zero divisors on $X_n$ , and is a rich algebro-geometric object with no analogue in the number field setting. From this point of view, the p-primary part of the motivic class group is the full p-divisible (Barsotti–Tate) group $J_{X_n}[{\kern1.3pt}p^{\infty }]$ , which is an inductive system of p-power group schemes. The p-primary part $\operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }]$ of the “physical” class group is none other than the group of k-rational points of $J_{X_n}[{\kern1.3pt}p^{\infty }]$ , which is only a very small piece of $J_{X_n}[{\kern1.3pt}p^{\infty }]$ ; for example, when $X_0=\mathbf {P}^1_k$ and $S=\{\infty \}$ (which is a prototypical case), the abelian group $\operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }]$ is trivial, whereas the p-divisible group $J_{X_n}[{\kern1.3pt}p^{\infty }]$ has height ${2g_n}$ with $g_n$ the genus of $X_n$ .

Our aim is to understand the structure—broadly construed—of the full p-divisible group $J_{X_n}[{\kern1.3pt}p^{\infty }]$ as $n\rightarrow \infty $ . Recent work provides some evidence that there should be an Iwasawa theory for these objects. By analyzing L-functions, Davis, Wan, and Xiao [DWX] prove that, for a certain class of ${\mathbf Z}_p$ -towers $\{X_n\}_{n\ge 0}$ with $X_0=\mathbf {P}^1$ and $S=\{\infty \}$ (a class which we call “basic” in what follows; see §2.12), the isogeny type of $J_{X_n}[{\kern1.3pt}p^{\infty }]$ over $\bar {k}$ behaves in a remarkably regular way as n grows (cf. [KMU1], [KMU2], [KZ], [RWX+], [X]). However, isogeny type is a somewhat coarse invariant, as it loses all touch with torsion phenomena. As a first and critical step toward understanding this more subtle torsion in the full p-divisible group, we will investigate the p-torsion group schemes $J_{X_n}[{\kern1.3pt}p]$ which are polarized “1-truncated Barsotti–Tate groups.” These objects have a rich and extensive history, yet despite being the focus of much research (e.g., [PU], [O2]) remain rather mysterious. The goal of this paper is to provide evidence—both theoretical and computational—for the following Iwasawa-theoretic principle.

Philosophy 1.1. For any ${\mathbf Z}_p$ -tower of curves $\{X_n\}_{n\ge 0}$ , the p-torsion group schemes $J_{X_n}[{\kern1.3pt}p]$ behave in a “regular” way as $n\rightarrow \infty $ .

As a first approximation to $J_{X_n}[{\kern1.3pt}p]$ , we will study the kernel of Frobenius $J_{X_n}[F]$ . Note that the quotient of $J_{X_n}[{\kern1.3pt}p]$ by $J_{X_n}[F]$ is canonically isomorphic to the Cartier dual of $J_{X_n}[F]$ . In this way, knowledge of $J_{X_n}[F]$ determines $J_{X_n}[{\kern1.3pt}p]$ up to a single extension. The virtue of focusing attention on $J_{X_n}[F]$ is that it can be understood explicitly via differentials on the curve $X_n$ . Indeed, the group scheme $J_{X_n}[F]$ functorially determines and is determined by its contravariant Dieudonné module, which by a theorem of Oda [O1] is naturally identified with the $k[V]$ -module $M_n:=H^0(X_n,\Omega ^1_{X_n/k})$ of global regular 1-forms on $X_n$ , with V acting as the Cartier operator. Thus, to analyze the growth of the group schemes $J_{X_n}[F]$ , we will study the $k[V]$ -module structure of $M_n$ as n grows. In this paper, we develop efficient algorithms to compute with differentials on ${\mathbf Z}_p$ -towers in order to provide computational evidence for Philosophy 1.1 and we prove instances of the philosophy when $p=2$ .

Let us describe our contributions in more detail. For each n, Fitting’s lemma gives a natural direct sum decomposition of $k[V]$ -modules

(1.1) $$ \begin{align} M_n=H^0(X_n,\Omega^1_{X_n/k}) = M_n^{V\text{-}\mathrm{nil}}\oplus M_n^{V\text{-}\mathrm{bij}}, \end{align} $$

where $M_n^{V\text {-}\mathrm {nil}}$ (resp. $M_n^{V\text {-}\mathrm {bij}}$ ) is the maximal $k[V]$ -submodule on which V is nilpotent (resp. bijective). As the ${\mathbf Z}_p$ -tower is totally ramified over the set S, the Deuring–Shafarevich formula [S5] provides a dimension formula for the p-rank

(1.2) $$ \begin{align} d_n:=\dim_k M_n^{V\text{-}\mathrm{bij}} = p^n (d_0 + |S| - 1) - (|S| -1), \end{align} $$

which is an instance of Philosophy 1.1. Moreover, one has an isomorphism of $\bar {k}[V]$ -modules

$$\begin{align*}M_n^{V\text{-}\mathrm{bij}}\otimes_k \bar{k} \simeq (\bar{k}[V]/(V-1))^{d_n}, \end{align*}$$

which with (1.2) provides a nearly complete understanding of the behavior of $M_n^{V\text {-}\mathrm {bij}}$ as n grows.

As for the V-nilpotent part, taken together the Riemann–Hurwitz and Deuring–Shafarevich formulae yield the dimension formula

(1.3) $$ \begin{align} \dim_k M_n^{V\text{-}\mathrm{nil}} = (g_n - d_n) = p^n (g_0-d_0) + \frac{1}{2}(p-1) \sum_{Q \in S} \sum_{i=1}^n p^{i-1} (s_Q(i) - 1), \end{align} $$

where $s_Q(i)$ is the ith break in the upper ramification filtration of $\Gamma $ at $Q\in S$ and $g_n$ is the genus of $X_n$ . As every point in S must be wildly ramified and the very nature of wild ramification forces $s_Q(i+1) \ge p s_Q(i) $ for all Q and i, if S is nonempty, there is a lower bound of the form $g_n \ge c p^{2n}$ with $c> 0$ (see [GK, Th. 1] and cf. [KW3, Th. 1.1] and [KW4]). In fact, it follows from class field theory (see [GK, Rem. 3]) that, for any sequence $\{s_i\}$ of positive integers satisfying $s_{i+1}\ge p s_i$ , there exists a $\Gamma $ -tower $\{X_n\}$ with $X_0=\mathbf {P}_k^1$ and $S=\{\infty \}$ in which $s_Q(i) \ge s_i$ . In other words, the dimension of $M_n^{V\text {-}\mathrm {nil}}$ can grow arbitrarily fast!

In order to have any hope of identifying regular structure in $M_n^{V\text {-}\mathrm {nil}}$ as $n\rightarrow \infty $ , we will therefore restrict our attention to towers in which the upper ramification breaks behave in a regular way. For the purposes of this introduction—and in much of this paper—we will focus on the class of basic ${\mathbf Z}_p$ -towers over $k=\mathbf F_p$ with ramification invariant d, given by the Artin–Schreier–Witt equation

$$\begin{align*}Fy - y = \sum_{\substack{i=1\\ p\nmid i}}^d [c_i x^i] \end{align*}$$

for $c_i \in \mathbf F_p$ and $c_d \neq 0$ (see §2.1 and Definition 2.12). Each such tower has base curve $X_0=\mathbf {P}^1$ and $S=\{\infty \}$ , with $s_{\infty }(n)=dp^{n-1}$ for $n\ge 1$ , so repeated applications of Riemann–Hurwitz show that such towers are genus stable [KW3], in the sense that the genus of the nth curve $X_n$ is given by a quadratic polynomial in $p^n$ with rational coefficients for $n\gg 0$ . Explicitly.

(1.4) $$ \begin{align} g_n = \frac{d}{2(p+1)} p^{2n} -\frac{1}{2}p^n + \frac{p+1-d}{2(p+1)} \quad \text{for} \quad n \ge 0, \end{align} $$

which is very much in the spirit of (1.2) and provides another validation of Philosophy 1.1. Note that any basic ${\mathbf Z}_p$ -tower has $M_n^{V\text {-}\mathrm {bij}}=0$ , so $\dim _k M_n^{V\text {-}\mathrm {nil}}=\dim _k H^0(X_n,\Omega ^1_{X_n/k}) = g_n$ .

As V is nilpotent on $M_n^{V\text {-}\mathrm {nil}}$ , for each n, the $k[V]$ -module structure of $M_n^{V\text {-}\mathrm {nil}}$ is completely determined by the sequence of positive integers

$$\begin{align*}a^{(r)}_n:=\dim_k \ker \left( V^r : H^0(X_n,\Omega^1_{X_n/k}) \rightarrow H^0(X_n,\Omega^1_{X_n/k})\right)\!. \end{align*}$$

The integer $a_n:=a_n^{(1)}$ is the a-number of the curve $X_n$ , and has been studied extensively [AMB+], [BC1], [DF], [E2], [EP], [F3], [FGM+], [J], [KW1], [MS], [R2], [WK], [Z]. For any fixed n and r sufficiently large, $V^r$ is zero on $M_n^{V\text {-}\mathrm {nil}}$ , so (1.3) gives a formula for $a_n^{(r)}$ in such cases. This relies on the Riemann–Hurwitz and Deuring–Shafarevich formulae; there is no analogous formula for the a-number. Indeed, as p-groups are solvable, the essential instances of the Riemann–Hurwitz and Deuring–Shafarevich formulae are for a branched ${\mathbf Z}/p{\mathbf Z}$ -cover $Y\rightarrow X$ of smooth projective curves over k, and in general the a-number of Y cannot be determined by the a-number of X and the ramification data of the covering. While [BC1] does provide bounds on the a-number of Y that depend only on the a-number of X and the ramification data, these bounds allow for considerable variation. For a basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d, the bounds imply

(1.5) $$ \begin{align} \frac{1}{2}\left(1-\frac{1}{p}\right)\left(1 - \frac{1}{p^2}\right) +O(p^{-n}) \le \frac{a_n}{g_n} \le \frac{2}{3}\left(1-\frac{1}{2p}\right) + O(p^{-n}), \end{align} $$

as $n\rightarrow \infty $ , with implicit constants depending only on d and p. If a basic ${\mathbf Z}_p$ -tower behaves like a “random” sequence of ${\mathbf Z}/p{\mathbf Z}$ -covers, we might guess that $a_n$ is asymptotically $\frac {1}{2}(1-p^{-1})(1-p^{-2})\cdot g_n$ , since a-numbers of random ${\mathbf Z}/p{\mathbf Z}$ -covers experimentally seem to be close to the lower bound with high probability [AMB+, Rem. 1.5(3)].

For any fixed basic ${\mathbf Z}_p$ -tower $\{X_n\}_{n\ge 0}$ and integer r, to compute $a_n^{(r)}$ , we must determine the matrix of $V^r$ and its kernel on the $g_n$ -dimensional space of holomorphic differentials of $X_n$ . As $g_n$ grows like $c p^{2n}$ with $c>0$ by (1.4), such computations rapidly become intractable, even for small values of p. A key contribution of the present paper is the development of much more efficient algorithms (implemented in Magma [BC2]) for computing with differentials on a ${\mathbf Z}_p$ -tower of curves in order to investigate the behavior of $a_n^{(r)}$ . After computing numerous examples, we are led to the following conjecture.

Conjecture 1.2. Let $\{X_n\}_{n\ge 0}$ be a basic ${\mathbf Z}_p$ -tower with ramification invariant d. For each positive integer r, there exist an integer $m> 0$ , a rational number $\lambda $ , and a periodic function $c: {\mathbf Z}/m{\mathbf Z} \rightarrow {\mathbf Q}$ such that

$$\begin{align*}a_n^{(r)} = \alpha(r,p) dp^{2n} + \lambda n + c(n)\quad\text{with}\quad \alpha(r,p) := \frac{r}{2(p+1)\left(r+\frac{p+1}{p-1}\right)} \end{align*}$$

for all n sufficiently large. If D is the prime-to-p part of the denominator of $\alpha (r,p)$ in lowest terms and $D>1$ , then m may be taken to be the multiplicative order of $p^2$ modulo D. When in addition $m=1$ , we may take $\lambda =0$ and c constant.

Remark 1.3. We compute that $\alpha (1,p) = \frac {p-1}{4p(p+1)}$ , so we may take $m=1$ and $\lambda =0$ when $r=1$ . In other words, we predict that the a-number of the nth level of a basic ${\mathbf Z}_p$ -tower with ramification invariant d is $\frac {p-1}{4 p (p+1)} d p^{2n} + c$ (with the constant c depending on the tower) for $n \gg 0$ .

We are able to prove Conjecture 1.2 when $p=2$ and $r=1$ .

Theorem 1.4 (See Corollary 8.12).

Let $\{X_n\}_{n\ge 0}$ be a basic ${\mathbf Z}_2$ -tower with ramification invariant d. Then, for $n>1$ ,

$$\begin{align*}a_n=a_n^{(1)} = \frac{d}{24}\cdot 2^{2n} + \frac{d + (-1)^{(d-1)/2}\cdot 3}{12} = \frac{d}{4}\frac{(2^{2n-1} +1)}{3} + \frac{(-1)^{(d-1)/2}}{4}. \end{align*}$$

Example 1.5. Igusa curves in characteristic 2 (rigidified using $\Gamma _1(5)$ ) form a basic ${\mathbf Z}_2$ -tower $\{X_n\}_{n\geq 0}$ . We have

$$\begin{align*}g(X_n) = 2^{2n-2}-2^{n}+1 \quad \text{and} \quad a(X_n) = 2^{2n-4} \text{ for } n>1. \end{align*}$$

See Examples 2.15 and 8.14.

Remark 1.6. Conjecture 1.2 indicates that the naïve guess that a ${\mathbf Z}_p$ -tower behaves like a sequence of “random” ${\mathbf Z}/p{\mathbf Z}$ -covers is wrong, as together with (1.4) it implies that $a_n/g_n$ approaches $\frac {1}{2}(1-p^{-1})$ and not $\frac {1}{2}(1-p^{-1})(1-p^{-2})$ as the guess would predict. In other words, a basic ${\mathbf Z}_p$ -tower has more structure than a “random” sequence of Artin–Schreier covers which force the a-numbers to be larger.

Remark 1.7. For a basic ${\mathbf Z}_p$ -tower $\{X_n\}_{n\ge 0}$ with ramification invariant d, and each $n\ge 1$ , we have an isomorphism of $k[V]$ -modules

$$\begin{align*}M_n^{V\text{-}\mathrm{nil}} = H^0(X_n,\Omega^1_{X_n/k}) \simeq \bigoplus_{i\ge 1} \left(\frac{k[V]}{V^i}\right)^{m_n(i)} \end{align*}$$

for uniquely determined nonnegative integers $m_n(i)$ . Conjecture 1.2 implies that for each i, there exist an integer $\ell>0$ , a rational number $\mu $ , and a periodic function $\gamma : {\mathbf Z}/\ell {\mathbf Z}\rightarrow {\mathbf Q}$ such that

$$\begin{align*}m_n(i) =\beta(i,p)\frac{dp^{2n}}{p-1} + \mu n + \gamma(n)\quad\text{with}\quad \beta(i,p)=\frac{1}{(i+\frac{p+1}{p-1})^3 - (i+\frac{p+1}{p-1})} \end{align*}$$

for all n sufficiently large, which shows that the $k[V]$ -module $H^0(X_n,\Omega ^1_{X_n/k})$ —and therefore the F-torsion in the motivic class group $J_{X_n}$ —behaves in an astonishingly regular manner as $n\rightarrow \infty $ .

To simplify this introduction, we have focused on basic ${\mathbf Z}_p$ -towers. Later, we will consider some other classes of towers and see that some form of Philosophy 1.1 continues to hold. Monodromy-stable towers behave like basic towers, while in other examples $a_n^{(r)}$ still appears regular but does not behave exactly as in Conjecture 1.2 (see §§3 and 6).

Remark 1.8. Writing $\mathscr {G}_{X_n}:=J_{X_n}[{\kern1.3pt}p^{\infty }]$ for the p-divisible group of the Jacobian of $X_n$ , there is a canonical decomposition of p-divisible groups

$$\begin{align*}\mathscr{G}_{X_n}=\mathscr{G}_{X_n}^{\text{'et}}\times \mathscr{G}_{X_n}^{\mathrm{mult}}\times \mathscr{G}_{X_n}^{\mathrm{ll}} \end{align*}$$

into étale, multiplicative, and local–local components. As $\operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }] = \mathscr {G}_{X_n}(k) = \mathscr {G}_{X_n}^{\text {'et}}(k)$ , the results of Mazur–Wiles, Crew, and Gold–Kiselevsky can be understood as theorems about the structure of $\mathscr {G}_{X_n}^{\text {'et}}$ . Indeed, generalizing [MW, Prop. 2], Crew [C2, §3] proves that for S nonempty and k algebraically closed, the projective limit $\varprojlim _n \operatorname {\mathrm {Hom}}_{k}(\mathscr {G}_{X_n}^{\text {'et}},{\mathbf Q}_p/{\mathbf Z}_p)$ is free of finite rank over $\Lambda $ , and deduces the structure of $\varprojlim _n \operatorname {\mathrm {Cl}}_{K_n}[{\kern1.3pt}p^{\infty }]$ for finite k from this result. The analogue of this result for the multiplicative part is provided by [C1], which treats arbitrary pro-p extensions of function fields, and allows S to be empty. The local–local components $\mathscr {G}_{X_n}^{\mathrm {ll}}$ are far more mysterious, and incorporate information about the structure of $M_n^{V\text {-}\mathrm {nil}}$ .

Remark 1.9. Continuing the notation of the previous remark, when S is empty, equation (1.3) reads $\operatorname {\mathrm {ht}}(\mathscr {G}_{X_n}^{\mathrm {ll}}) = 2p^n(g_0-h_0)$ . As in the cases of the étale and multiplicative components, this is a numerical shadow of a much deeper fact: the “limit” Dieudonné module is free of rank $2(g_0-h_0)$ over $\Lambda _W:=W(k)[\![\Gamma ]\!]$ (see [C1]). Using familiar arguments from Iwasawa theory, this structural result gives complete control over $\mathscr {G}_{X_n}^{\mathrm {ll}}$ as n grows. In particular, for each étale ${\mathbf Z}_p$ -tower and positive integer r, there exist $b_r , c_r \in {\mathbf Q}$ such that $a^{(r)}_n = b_r p^n + c_r$ for $n \gg 0$ .

This is very different than the behavior for ramified ${\mathbf Z}_p$ -towers. When S is nonempty, the $\Lambda _W$ -module $\mathbf {D}_{\infty }^{\mathrm {ll}}=\varprojlim _n \mathbf {D}(\mathscr {G}_{X_n}^{\mathrm {ll}})$ is never finitely generated [C1]. One might hope to tame such wild behavior by suitably enlarging the Iwasawa algebra, and indeed the canonical Frobenius and Verschiebung morphisms give $\mathbf {D}_{\infty }^{\mathrm {ll}}$ the structure of a (left) module over the “Iwasawa Dieudonné”-ring $\Lambda _W[\![ F,V]\!]$ . However, it follows from (1.5) that $\mathbf {D}_{\infty }^{\mathrm {ll}}$ is not finitely generated over $\Lambda _W[\![F,V]\!]$ either! Indeed, writing $M_n:=\mathbf {D}(\mathscr {G}_n^{\mathrm {ll}})$ and $M_{\infty }:=\varprojlim M_n$ , the canonical projections $M_{\infty } \rightarrow M_n$ are all surjective, so if $M_{\infty }$ were generated by $\delta $ generators over $\Lambda _W[\![F,V]\!]$ , then the same would be true of $M_n/(F,V)M_n$ as a module over $k[\Gamma /\Gamma _n]$ ; in particular, the k-dimension of $M_n/(F,V)M_n$ would be bounded above by $\delta |\Gamma /\Gamma _n|=\delta p^n$ . However, we have a natural identification

$$ \begin{align*} M_n/(F,V)M_n = \operatorname{\mathrm{coker}}\left( V: H^0(X_n,\Omega^1_{X_n/k} )^{V\text{-}\mathrm{nil}} \rightarrow H^0(X_n,\Omega^1_{X_n/k} )^{V\text{-}\mathrm{nil}}\right) \end{align*} $$

and the dimension of this cokernel is none other than the a-number $a_n$ of $X_n$ . As $a_n$ is bounded below by $cp^{2n}$ with $c>0$ thanks to (1.5), the putative upper bound of $\delta p^n$ is violated for $n \gg 0$ .

Remark 1.10. Iwasawa theory usually considers the p-part of the class group, not the p-torsion, whereas in this paper, we mainly look at the p-torsion in the motivic class group $J_{X_n}$ . However, the usual Iwasawa-theoretic arguments give similar results about the p-torsion in class groups of number fields (see [M2] for an example where this is spelled out [in a more general setting]).

1.2 Overview of the paper

As previously discussed, the goal of this paper is to provide computational and theoretic evidence of Philosophy 1.1. Section 2 reviews information about ${\mathbf Z}_p$ -towers of curves, Artin–Schreier–Witt theory, and invariants of towers. Section 3 formulates a more general version of the conjecture in the introduction for monodromy-stable towers, which are one natural class of towers to consider.

Sections 4 and 5 are the computational heart of the paper, providing an extensive set of examples ² which support the conjecture for basic towers. Section 4 focuses on the a-number, whereas §5 addresses higher powers of the Cartier operator. Section 6 presents some examples that support our conjectures for monodromy-stable towers which are not basic and that suggest that Philosophy 1.1 continues to hold for nonmonodromy-stable towers.

In §7, we describe an algorithm which we have implemented in the Magma computer algebra system [BCP] that lets us produce these examples. Computer algebra systems like Magma have the ability to compute a matrix representing the Cartier operator on the space of regular differentials on any smooth projective curve over a finite field. We work in the special setting that the tower is based over the projective line and is totally ramified over the point at infinity and unramified elsewhere. Our algorithm is much faster as it takes advantage of the structure of a ${\mathbf Z}_p$ -tower and incorporates as much theoretical information as possible. In particular, when a ${\mathbf Z}_p$ -tower is presented in a standard form, we are able to use results of Madden [M1] to obtain a simple basis for the space of regular differentials on each curve in the tower which greatly accelerates the computations. This efficiency is crucial, as the genus of the curves in a ${\mathbf Z}_p$ -tower very quickly become too large for the generic methods provided by Magma to handle. Our algorithm is efficient enough that we are able to compute sufficiently many levels of ${\mathbf Z}_p$ -towers with small p to provide convincing evidence for our conjectures.

Section 8 is the theoretical heart of the paper, where we prove special cases of our conjectures when $p=2$ . We do so by proving a general result (valid in any characteristic) about the trace of differentials on an Artin–Schreier cover that are killed by the Cartier operator. When $p=2$ , this is enough to gain control over the a-number. These ideas give only very limited information about higher powers of the Cartier operator, even in characteristic 2 (§8.3).

Remark 1.11. Computations in this paper were done using Magma 2.25-6 and 2.25-8 [BCP] running on several different personal computers ³ and a server at the University of Canterbury. Thus, running times for different examples are not directly comparable as they may have been run on different machines, although they are of a similar magnitude. When directly comparing running times, the same computer was used.

Notation 1.12. In the rest of the paper, we often want to compare multiple ${\mathbf Z}_p$ -towers simultaneously while also avoiding excessive subscripts. To do so, we adopt the following notation.

• • For a tower of curves $\mathcal {T}$ , we let $\mathcal {T}(n)$ denote the nth level of the tower.

• • For a curve X, we use the notation $g(X)$ , $a(X)$ , and $a^r(X)$ for the genus, a-number, and dimension of the kernel of the rth power of $V_X$ on the space of regular differentials.

• • We let $J_{X}$ denote the Jacobian of X.

• • Given a tower $\mathcal {T}$ and point Q in the base curve, Notation 2.5 introduces invariants $s_Q(\mathcal {T}(n))$ , $u_Q(\mathcal {T}(n))$ , and $d_Q(\mathcal {T}(n))$ , which reflect the ramification of $\mathcal {T}(n)$ over Q.

Notations 3.3 and 5.1 give constants $\alpha (r,p)$ and $m(r,p)$ appearing in our conjectures.

2 Towers of curves

Fix a perfect field k of characteristic $p>0$ . By a curve over k, we mean a smooth, projective, geometrically connected, k-scheme of dimension 1. We refer to a branched cover $\pi : Y \to X$ simply as a cover. We view the branch locus as a set of $\bar {k}$ -points of X. We say that the cover is Galois (resp. has Galois group G) if the corresponding extension of function fields is Galois (resp. has Galois group G).

2.1 Artin–Schreier–Witt theory and ${\mathbf Z}_p$ -towers

Definition 2.1. A ${\mathbf Z}_p$ -tower of curves $\mathcal {T}$ is a sequence of curves over k

$$\begin{align*}\mathcal{T}: \cdots \to \mathcal{T}(3) \to \mathcal{T}(2) \to \mathcal{T}(1) \to \mathcal{T}(0) \end{align*}$$

such that $\mathcal {T}(n)$ is a Galois (branched) cover of $\mathcal {T}(0)$ with $\operatorname {\mathrm {Gal}}(\mathcal {T}(n)/\mathcal {T}(0)) \simeq {\mathbf Z}_p /p^n {\mathbf Z}_p \simeq {\mathbf Z}/p^n{\mathbf Z}$ , for $n \geq 1$ . We assume that there is a finite nonempty set S of $\bar {k}$ -points of $\mathcal {T}(0)$ such that $\mathcal {T}(n)\rightarrow \mathcal {T}(0)$ étale outside of S and totally ramified over every point of S, for all n. We refer to $\mathcal {T}(n)$ as the nth level (or nth layer) of the tower, and to $\mathcal {T}(0)$ as the base of the tower.

As we define curves to be geometrically connected, our ${\mathbf Z}_p$ -towers are automatically geometric towers in the sense that all $\mathcal {T}(n)$ have constant field k.

We can equivalently describe a tower of curves as a ${\mathbf Z}_p$ -tower of function fields $k(\mathcal {T}(n))$ . All ${\mathbf Z}_p$ -towers of curves (equivalently function fields) can be described by Artin–Schreier–Witt theory. This goes back to [W]: an accessible recent reference is [KW2, §3], which builds on the theory of Witt vectors which are briefly reviewed in [KW2, §2] and more extensively reviewed in [R1]. We mainly need the following special cases, which describe ${\mathbf Z}_p$ -extensions of $k(\!(t)\!)$ (which are local) and ${\mathbf Z}_p$ -towers over the projective line.

Let $W(K)$ denote the Witt vectors of the characteristic p field K with Frobenius F, and let $\wp : W(K) \to W(K)$ be given by $\wp (y) := Fy -y$ . We write $[\cdot ]:K\rightarrow W(K)$ for the Teichmüller map, which is the unique multiplicative section to the canonical projection $W(K)\rightarrow K$ onto the first Witt component. Let v be the p-adic valuation on $W(k)$ normalized, so $v(p)=1$ .

Fact 2.2. Let k be a finite field of characteristic p, and fix an element $\alpha $ of k such that $\operatorname {\mathrm {tr}}_{k/\mathbf F_p}(\alpha ) \neq 0$ . All ${\mathbf Z}_p$ -extensions of $K = k(\!(t)\!)$ may be obtained by adjoining a solution $y_1,y_2,\ldots $ of the equation

(2.1) $$ \begin{align} \wp((y_1,y_2,\ldots)) = F(y_1,y_2,\ldots) - (y_1,y_2,\ldots) = c [\alpha] + \sum_{\gcd(i,p) =1} c_i [t^{-i}] \end{align} $$

in $W(k(\!(t)\!) )$ , where $c_i \in W(k)$ and $c_i \to 0$ as $i \to \infty $ . The unique ${\mathbf Z}/p^n{\mathbf Z}$ -subextension $K_n$ arises from adjoining $y_1,y_2,\ldots ,y_n$ to K, and depends only on the right side modulo $p^n$ .

The conductor of $K_n$ over K is $(t^{u_n})$ , where

$$\begin{align*}u_n = \begin{cases} 1 + \max \{ i p^{n-1-v(c_i)} : \gcd(i,p)=1, \, v(c_i) < n \}, & \textrm{if there exists } i \textrm{ such that } v(c_i) <n,\\ 0, & \textrm{otherwise}. \end{cases} \end{align*}$$

This is [KW3, Exam. 2.4 and Props. 3.1 and 3.3]. Note that this is a local statement, whereas the next fact is a global statement.

Fact 2.3. Let k be a finite field of characteristic p, and fix an element $\alpha $ of k such that $\operatorname {\mathrm {tr}}_{k/\mathbf F_p}(\alpha ) \neq 0$ . All ${\mathbf Z}_p$ -extensions of $K = k(x)$ ramified over a set $S \subset \mathbf {P}^1_k(\bar {k})$ may be obtained by adjoining a solution $y_1,y_2,\ldots $ of the equation

$$\begin{align*}\wp((y_1,y_2,\ldots)) = F(y_1,y_2,\ldots) - (y_1,y_2,\ldots) = c [\alpha] + \sum_{Q \in S} \sum_{\gcd(i,p) =1} c_{Q,i} [\pi_Q^{-i}], \end{align*}$$

with $c \in W(k)$ , $c_{Q,i} \in W(\bar {k})$ , and with $\pi _Q = x - Q$ if $Q \in \bar {k}$ and $\pi _Q = 1/x$ if $Q = \infty $ , such that:

1. 1. for $\sigma \in \operatorname {\mathrm {Gal}}(\bar {k}/k)$ and $Q \in \mathbf {P}^1_k(\bar {k})$ , we have $\sigma c_{Q,i} = c_{\sigma Q,i}$ ;

2. 2. for every integer $n \geq 1$ , there exists finitely many $c_{Q,i}$ with $v(c_{Q,i}) < n$ .

The unique ${\mathbf Z}/p^n{\mathbf Z}$ -subextension $K_n$ arises from adjoining $y_1,y_2,\ldots ,y_n$ to K, and depends only on the right side modulo $p^n$ . The tower is geometric if there exists a $c_{Q,i}$ with valuation $0$ .

Again see [KW3], especially Proposition 4.9.

Remark 2.4. The first level of these extensions (given by adjoining $y_1$ , or equivalently working in the truncated Witt vectors $W_1(K)$ and with the right side modulo p) is Artin-Schreier extensions. For example, (2.1) becomes

$$ \begin{align*}y_1^p - y_1 = c \alpha + \sum_{\substack { \gcd(i,p)=1 \\ v(c_i) =0 }} c_i t^{-i}. \end{align*} $$

Similarly, the unique ${\mathbf Z}/p^n{\mathbf Z}$ -extension of $L=K(\{y_i\})$ can be described using the truncated Witt vectors $W_n(K)$ . Recall that arithmetic with Witt vectors is not done componentwise, and is highly nontrivial. In particular, while $[c x^i] = (c x^i,0,0,\ldots )$ , the sum $[c_i x^i] + [c_j x^j]$ is not $(c_i x^i + c_j x^j,0,0,\ldots )$ .

2.2 Ramification and conductors in towers

Notation 2.5. Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower of curves over k, and let $Q\in S$ .

1. 1. Let $d_{Q}(\mathcal {T}(n))$ be the unique break in the lower ramification filtration of the cover $\mathcal {T}(n) \to \mathcal {T}(n-1)$ at the point above Q (the ramification invariant above Q).

2. 2. Let $s_Q(\mathcal {T}(n))$ be the largest break in the upper ramification filtration for the cover $\mathcal {T}(n) \to \mathcal {T}(0)$ above Q.

3. 3. When k is finite, ⁴ let $u_Q(\mathcal {T}(n))$ be the exponent of the conductor for the extension of local fields coming from $\mathcal {T}(n)_Q \to \mathcal {T}(0)_Q$ .

Recall that the upper numbering is compatible with quotients, so we can give $\mathcal {T}$ an upper ramification filtration making $s_Q(\mathcal {T}(n))$ the nth (upper) break above Q. The lower numbering is compatible with subgroups, and hence the largest break in the lower ramification filtration of $\mathcal {T}(n) \to \mathcal {T}(0)$ above Q is $d_Q(\mathcal {T}(n))$ .

Lemma 2.6. Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower of curves over k, and let $Q\in S$ . For each positive integer n:

1. 1. $\displaystyle d_Q(\mathcal {T}(n)) = p^{n-1} s_Q(\mathcal {T}(n)) - \sum _{j=1}^{n-1} \varphi (p^{{\kern1.2pt}j}) s_Q(\mathcal {T}(j))$ ;

2. 2. $d_Q(\mathcal {T}(n+1)) - d_Q(\mathcal {T}(n)) = \left (s_Q(\mathcal {T}(n+1)) - s_Q(\mathcal {T}(n)) \right ) p^n $ ;

3. 3. if k is finite, $u_Q(\mathcal {T}(n)) = s_Q(\mathcal {T}(n))+1$ .

Proof. This result is standard, although we do not know a good reference for this exact statement. The relationship between the breaks in the upper and lower ramification filtrations in a ${\mathbf Z}/p^n{\mathbf Z}$ -extension of local fields is spelled out in [S1, Exam. IV.3]. There exist positive integers $i_0, i_1, \ldots , i_{n-1}$ such that the breaks in the upper numbering filtration are $i_0, i_0 + i_1, \ldots , i_0 + i_1 + \cdots + i_n$ and the breaks in the lower numbering filtration are $i_0, i_0 + p i_1, \ldots , i_0 + p i_1 + \cdots p^{n-1} i_{n-1}$ . In particular, $s_Q(\mathcal {T}(j)) = i_0 + i_1 + \cdots + i_{j-1}$ and $d_Q(\mathcal {T}(n)) = i_0 + p i_1 + \cdots + p^{n-1} i_{n-1}$ , and (1) follows. Statement (2) is a formal consequence of the previous part. When k is finite, the relationship between the conductor and the upper ramification breaks in (3) follows from [S1, §XV.2, Cor. 2 to Th. 1].

Lemma 2.7. Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower totally ramified above a finite set S of $\bar {k}$ -points of $\mathcal {T}(0)$ . Then,

$$ \begin{align*} 2 g(\mathcal{T}(n)) -2 &= p^n ( 2 g(\mathcal{T}(0))-2) + \sum_{Q \in S} \sum_{i=1}^n \varphi(p^{n+1-i}) (d_Q(\mathcal{T}(i)) +1 ) \\ &= p^n ( 2 g(\mathcal{T}(0))-2)) + \sum_{Q \in S} \sum_{i=1}^n \varphi(p^i) (s_Q(\mathcal{T}(i))+1). \end{align*} $$

Proof. Apply the Riemann–Hurwitz formula.

Remark 2.8. As remarked in the introduction, for ${\mathbf Z}_p$ -towers in characteristic p, there is always “a lot” of ramification. In particular, if $\mathcal {T}$ is totally ramified above Q, then $s_Q(\mathcal {T}(n)) \geq p s_Q(\mathcal {T}(n-1))$ . Using Lemma 2.6(1) to convert to the lower ramification filtration, it follows that $d_Q(\mathcal {T}(n)) \geq (p^2-p+1) d_Q(\mathcal {T}(n-1))$ . Using Lemma 2.7, for any ramified ${\mathbf Z}_p$ -tower, there is a constant $c>0$ such that $g(\mathcal {T}(n)) \geq c p^{2n}$ .

2.3 Types of towers

We next identify several nice kinds of ${\mathbf Z}_p$ -towers which we will focus on.

Definition 2.9. Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower of curves over k with branch locus S.

1. 1. We say that $\mathcal {T}$ is monodromy-stable, or has stable monodromy, if for every $Q \in S$ , there exist $c_Q, d_Q \in {\mathbf Q}$ such that for $n \gg 0$ ,

   $$\begin{align*}s_Q(\mathcal{T}(n)) = c_Q + d_Q p^{n-1}. \end{align*}$$

2. 2. We say that $\mathcal {T}$ has periodically stable monodromy, or is periodically monodromy-stable, if for every $Q \in S$ , there exist an integer $m_Q$ , a $d_Q \in {\mathbf Q}$ , and a function $c_Q : {\mathbf Z}/m_Q {\mathbf Z} \to {\mathbf Q}$ such that for $n \gg 0$ ,

   $$\begin{align*}s_Q(\mathcal{T}(n)) = c_Q(n) + d_Q p^{n-1}. \end{align*}$$

As the Riemann–Hurwitz formula determines the genus of a cover in terms of the genus of the base curve and the ramification, the genus of a monodromy-stable (resp. periodically monodromy-stable) ${\mathbf Z}_p$ -tower is of the form $a p^{2n} + b p^n + c$ for $n \gg 0$ (resp. is of the form $a(n) p^{2n} + b(n) p^n + c(n)$ , where $a,b,c$ are eventually periodic functions). This behavior is referred to as being genus stable (resp. periodically genus stable). For later use, we record the following lemma.

Lemma 2.10. If $\mathcal {T}$ is monodromy-stable and $Q\in S$ with $s_Q(\mathcal {T}(n)) = c_Q + d_Q p^{n-1}$ for $n \gg 0$ , then there exists $c^{\prime }_Q \in {\mathbf Q}$ such that

$$\begin{align*}d_Q(\mathcal{T}(n)) = d_Q \frac{p^{2n-1}}{p+1} + c^{\prime}_Q \text{ for } n \gg 0. \end{align*}$$

Furthermore, $g(\mathcal {T}(n))$ is asymptotically $ \displaystyle \left ( \sum _{Q \in S} d_Q \right ) \frac { p^{2n}}{2 (p+1)} $ .

Proof. For the first, use the definition of monodromy stability plus Lemma 2.13(2). Then the second statement follows using Lemma 2.7.

Remark 2.11. Monodromy-stable towers are a very natural class of towers to consider as all ${\mathbf Z}_p$ -towers of “geometric origin” are monodromy-stable [KM2].

Many of our computations will deal with a particularly simple class of ${\mathbf Z}_p$ -towers over $\mathbf {P}^1_k$ where k is finite, which we refer to as basic ${\mathbf Z}_p$ -towers. Fix a coordinate x on the projective line $\mathbf {P}^1_k$ .

Definition 2.12. Let d be a positive integer that is prime to p, and let k be a finite field of characteristic p. A basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d is the ${\mathbf Z}_p$ -tower over $\mathbf {P}^1_k$ given by the Artin–Schreier–Witt equation

$$\begin{align*}Fy - y = \sum_{\substack{i=1 \\ (i,p)=1}}^d [c_i x^i] \end{align*}$$

with $c_i \in k$ and $c_d \neq 0$ . (It is convenient to then define $c_i =0$ when $p | i$ .)

These are also called unit-root ${\mathbf Z}_p$ -extensions [KW3, Exam. 4.10]. By Fact 2.3, the function field of $\mathcal {T}(n)$ is the ${\mathbf Z}/ p^n {\mathbf Z}$ -extension of $k(x)$ given by adjoining $y_1,y_2,\ldots , y_n$ where $(y_1,y_2,\ldots ,y_n) \in W_n(k(x))$ is a solution of the Witt vector equation

(2.2) $$ \begin{align} F(y_1,y_2,\ldots,y_n) - (y_1,y_2,\ldots,y_n) = \sum_{i=1}^d (c_i x^i,0,\ldots, 0). \end{align} $$

In particular, $\mathcal {T}(1)$ is the Artin–Schreier curve given by $\displaystyle y_1^p - y_1 = \sum _{i=1}^d c_i x^i$ .

Lemma 2.13. A basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d is totally ramified over $\infty $ and unramified elsewhere. Recalling Notation 2.5, we have that

$$\begin{align*}u_{\infty}(\mathcal{T}(n)) -1 = s_{\infty}(\mathcal{T}(n)) = d p^{n-1} \quad \text{and that} \quad d_{\infty}(\mathcal{T}(n)) = d \cdot \frac{p^{2n-1} +1}{p+1}. \end{align*}$$

In particular, basic ${\mathbf Z}_p$ -towers are monodromy-stable (recall Definition 2.9) and the genus satisfies

$$\begin{align*}2 g(\mathcal{T}(n)) -2 = \frac{d}{p+1} p^{2n} - p^n - \frac{p+1+d}{p+1}. \end{align*}$$

Proof. We see that $u_{\infty }(\mathcal {T}(n)) = 1 + d p^{n-1}$ using Fact 2.2. By Lemma 2.13, we obtain the formulas for $s_{\infty }(\mathcal {T}(n))$ , $d_{\infty }(\mathcal {T}(n))$ , and $g(\mathcal {T}(n))$ . See also [KW3, Exam. 4.10].

Remark 2.14. When working with a basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ , each layer $\mathcal {T}(n)\rightarrow \mathcal {T}(0)=\mathbf {P}^1_k$ is totally ramified over the point at infinity, and unramified elsewhere. We will therefore often write $u(\mathcal {T}(n))$ instead of $u_{\infty }(\mathcal {T}(n))$ (and similarly for $s(\mathcal {T}(n))$ and $d(\mathcal {T}(n))$ ).

Another nice example of a monodromy-stable tower is the Igusa tower.

Example 2.15. We work over $k=\overline {\mathbf F}_p$ , and let $\operatorname {\mathrm {Ig}}(n)$ denote the curve representing the moduli problem of elliptic curves over k with an Igusa-level structure of level $p^n$ and a $\mathscr {P}$ -level structure for a suitable auxiliary moduli problem $\mathscr {P}$ (see [KM1, Chap. 12]).

For example, when $p \neq 5$ , we could choose to use $\mathscr {P} = \Gamma _1(5)$ , which satisfies the hypotheses of [KM1, Th. 12.9.1], as the auxiliary moduli problem. (It is standard to compute that the moduli problem $\Gamma _1(5)$ has degree $24$ and has four cusps.) Note that $\operatorname {\mathrm {Ig}}(n)$ is a smooth proper curve over k, and it is connected. (It suffices to check this for $X_1(5)$ over $\mathbf C$ .) Then $\operatorname {\mathrm {Ig}}(1)$ is a $({\mathbf Z}/p{\mathbf Z})^{\times } / \{\pm 1\}$ -cover of $X_1(5)_k \simeq \mathbf {P}^1_k$ totally ramified over the supersingular points and [KM1, Cor. 12.9.4] gives a ${\mathbf Z}_p$ -tower

$$\begin{align*}\operatorname{\mathrm{Ig}} : \cdots \to \operatorname{\mathrm{Ig}}(3) \to \operatorname{\mathrm{Ig}}(2) \to \operatorname{\mathrm{Ig}}(1) , \end{align*}$$

totally ramified over the $p-1$ points S of $\operatorname {\mathrm {Ig}}(1)$ which lie over the supersingular points of $X_1(5)_k$ , and unramified elsewhere. We know that $d_Q(\operatorname {\mathrm {Ig}}(n)) = p^{2(n-1)}-1$ for each $Q \in S$ by [KM1, Lem. 12.9.3], which implies that $g(\operatorname {\mathrm {Ig}}(n)) = p^{2n-1} (p-1)/2 - 2 p^{n-1}(p-1) + 1$ as in [KM1, Cor. 12.9.4].

3 Conjectures for monodromy-stable towers

For a ${\mathbf Z}_p$ -tower of curves $\mathcal {T}$ over a perfect field of characteristic p, Philosophy 1.1 predicts that the invariants of $J_{\mathcal {T}(n)}[{\kern1.3pt}p]$ should be “regular” for $n \gg 0$ . This regularity should furthermore depend only on the local information given by the ramification filtration at each ramified point.

Philosophy 3.1. For a ${\mathbf Z}_p$ -tower of curves $\mathcal {T}$ over a perfect field of characteristic p ramified over S, invariants of $J_{\mathcal {T}(n)}[{\kern1.3pt}p]$ should be a sum of “local contributions” depending only on the ramification of $\mathcal {T}$ at each branch point $Q\in S$ .

Remark 3.2. The genus and p-rank of a monodromy-stable tower illustrate this philosophy as they include a contribution from each point of ramification. See, for example, the asymptotic for the genus in Lemma 2.10 and equation (1.2).

In this section, we formulate precise conjectures for monodromy-stable ${\mathbf Z}_p$ -towers that exemplify these philosophies. We make these conjectures only for $a^{r}(\mathcal {T}(n))$ with $r \geq 1$ , which are a partial list of invariants for $J_{\mathcal {T}(n)}[{\kern1.3pt}p]$ . We restrict ourselves in this manner as:

• • the ramification is simple in monodromy-stable towers, so it is much easier to see how $a^{r}(\mathcal {T}(n))$ is “regular” for $n \gg 0$ ;

• • it is feasible to compute with them: $a^{r}(\mathcal {T}(n))$ can be computed using the action of the Cartier operator on the space of regular differentials, and in monodromy-stable towers, the dimension of this vector space (the genus) is “only” asymptotic to $c p^{2n}$ with $c>0$ . Other ${\mathbf Z}_p$ -towers with more complicated ramification will usually have even faster genus growth.

We begin by considering the asymptotic growth of $a^{r}(\mathcal {T}(n))$ in monodromy-stable ${\mathbf Z}_p$ -towers.

Notation 3.3. For a prime p and positive integers d and r, define

(3.1)

We will also use the shorthand .

Conjecture 3.4. Let $\mathcal {T}$ be a monodromy-stable ${\mathbf Z}_p$ -tower totally ramified over S and unramified elsewhere. For $Q \in S$ , let $c_Q, d_Q \in {\mathbf Q}$ with $s_Q(\mathcal {T}(n)) = d_Q p^{n-1} + c_Q$ for $n \gg 0$ and set . Then $a^{r}(\mathcal {T}(n))$ is asymptotically $\alpha (r,p) D p^{2n}$ for large n; in other words,

$$\begin{align*}\lim_{n \to \infty} \frac{a^{r}(\mathcal{T}(n))}{\alpha(r,p) D p^{2n}} =1. \end{align*}$$

Corollary 3.5. Conjecture 3.4 implies that for a totally ramified monodromy-stable ${\mathbf Z}_p$ -tower $\mathcal {T}$ ,

(3.2) $$ \begin{align} \lim_{n \to \infty} \frac{a^{r}(\mathcal{T}(n))}{g(\mathcal{T}(n))} = \frac{r (p-1)}{(p-1)r + (p+1)} = \frac{1}{1 + \frac{p+1}{(p-1) r}}. \end{align} $$

Proof. For $Q \in S$ , as before, let $s_Q(\mathcal {T}(n)) = d_Q p^{n-1} + c_Q$ for $n \gg 0$ with $c_Q, d_Q \in {\mathbf Q}$ and set . From Lemma 2.10, we know that $g(\mathcal {T}(n)$ is asymptotic to $D/ (2(p+1)) p^{2n}$ . Then compare with the asymptotic for $a^{r}(\mathcal {T}(n))$ from Conjecture 3.4.

For example, in monodromy-stable towers, we predict that

(3.3) $$ \begin{align} \displaystyle \lim_{n \to \infty} \frac{a(\mathcal{T}(n))}{g(\mathcal{T}(n)} = \frac{p-1}{2p}. \end{align} $$

Remark 3.6. The limit in Corollary 3.5 approaches $1$ as r becomes large. Thus, Conjecture 3.4 predicts that the Cartier operator is essentially nilpotent on $H^0(\Omega ^1_{\mathcal {T}(n)})$ . This is as expected: the $k[V_{\mathcal {T}(n)}]$ -module $H^0(\Omega ^1_{\mathcal {T}(n)})$ decomposes as a direct sum of its $V_{\mathcal {T}(n)}$ -nilpotent and $V_{\mathcal {T}(n)}$ -bijective submodules as in (1.1), and the Deuring–Shafarevich formula (1.2) shows that the k-dimension of the $V_{\mathcal {T}(n)}$ -bijective component is bounded by a constant times $p^n$ , whereas the genus (and hence the k-dimension of the $V_{\mathcal {T}(n)}$ -nilpotent component) is on the order of $p^{2n}$ . In other words, the Cartier operator acts nilpotently on essentially all of $H^0(\Omega ^1_{\mathcal {T}(n)})$ as $n\rightarrow \infty $ .

We also formulate more precise conjectures about the exact values of $a(\mathcal {T}(n))$ and $a^{r}(\mathcal {T}(n))$ in monodromy-stable towers. We begin with the a-number, whose behavior seems simplest.

Conjecture 3.7. For every monodromy-stable ${\mathbf Z}_p$ -tower of curves $\mathcal {T}$ over a perfect field of characteristic p, there exist $a,b,c \in {\mathbf Q}$ such that

$$\begin{align*}a(\mathcal{T}(n)) = a^{1}(\mathcal{T}(n)) = a p^{2n} + b p^n + c \text{ for } n \gg 0. \end{align*}$$

Note that Conjecture 3.4 predicts the value of a in Conjecture 3.7.

Conjecture 3.8. Fix $r \geq 1$ . For every monodromy-stable ${\mathbf Z}_p$ -tower of curves $\mathcal {T}$ over a perfect field of characteristic p, there exists a positive integer m and functions $a,b,c,\lambda : {\mathbf Z}/m{\mathbf Z} \to {\mathbf Q}$ such that

$$\begin{align*}a^{r}(\mathcal{T}(n)) = a(n) p^{2n} + b(n) p^n + c(n) + \lambda(n) n \text{ for } n \gg 0. \end{align*}$$

Again, Conjecture 3.4 predicts that the function $a(n)$ in Conjecture 3.8 is a constant function taking on a specific value. Writing $s_Q(\mathcal {T}(n)) = d_Q p^{n-1} + c_Q$ for $Q\in S$ and $n \gg 0$ with $c_Q, d_Q \in {\mathbf Q}$ , it predicts that

$$ \begin{align*} a(n) = \alpha(r,p) \left( \sum_{Q \in S} d_Q \right)\!. \end{align*} $$

In §§4–6, we provide evidence for these conjectures. We mainly focus on basic ${\mathbf Z}_p$ -towers as they are easiest to compute with; note that Conjecture 1.2, which addressed basic towers, is compatible with these more general conjectures. We then give some additional examples of other monodromy-stable towers as well as a few examples featuring nonmonodromy-stable towers that support Philosophy 1.1 while exhibiting more complicated behavior.

Remark 3.9. Towers with periodic, nonstable monodromy do not seem to satisfy Conjecture 3.7. There does appear to be similar formula for the a-number, but unsurprisingly the constants depend on the parity of n. However, limited investigations suggest that towers with periodic monodromy may satisfy Conjecture 3.8 as well (see §6.4).

Remark 3.10. We are not completely confident that monodromy-stable ${\mathbf Z}_p$ -towers are the correct class of ${\mathbf Z}_p$ -towers to consider. After this paper first appeared as a preprint, Joe Kramer-Miller and James Upton suggested that these conjectures might only hold for overconvergent ${\mathbf Z}_p$ -towers. Basic towers are both monodromy-stable and overconvergent, so since most of our evidence comes from computing with basic towers, it is difficult to investigate the difference.

4 a-numbers for basic towers

We first focus on the a-number of curves in basic ${\mathbf Z}_p$ -towers $\mathcal {T}$ (Definition 2.12) with ramification invariant d. By Lemma 2.13 (and noting Remark 2.14), we have $s(\mathcal {T}(n)) = d p^{n-1}$ . Unwinding Notation 3.3, we see that

$$\begin{align*}\alpha(p) = \alpha(1,p) = \frac{(p-1)}{4 (p+1) p}. \end{align*}$$

In this case, Conjecture 3.4 predicts that

(4.1) $$ \begin{align} \lim_{n \to \infty} \frac{a(\mathcal{T}(n))}{\alpha(p) d p^{2n}} = 1. \end{align} $$

We now present a refinement of Conjecture 3.7 and the $r=1$ case of Conjecture 1.2.

Conjecture 4.1. For every basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d, there exists a positive integer $N_d$ (depending only on d and p) and $c \in \mathbf {Q}$ (depending on $\mathcal {T}$ ) such that

$$\begin{align*}a(\mathcal{T}(n)) = a^{1}(\mathcal{T}(n)) = \alpha(p) d p^{2n} + c \text{ for } n \geq N_d. \end{align*}$$

Note that $ \alpha (p) d p^{2n} $ need not be an integer, but it is straightforward to check that $\alpha (p) d (p^{2n}-p^2)$ is always an integer when $p> 2$ . Thus, for convenience, we define

(4.2)

Conjecture 4.1 for a basic tower $\mathcal {T}$ with ramification invariant d is equivalent to $\delta _d(\mathcal {T}(n))$ being constant for sufficiently large n.

4.1 Examples in characteristic 3

We begin by focusing on ${\mathbf Z}_3$ -towers in characteristic $3$ , which we analyzed using the methods of §7.

Example 4.2. Let $p=3$ and $d=7$ . Consider the basic towers

$$\begin{align*}\mathcal{T}_1 : Fy - y = [x^7], \quad \mathcal{T}_2 : Fy -y = [x^{7}] -[x^{5}] -[x^{2}], \quad \mathcal{T}_3 : Fy-y = [x^{7}] - [x^{5}]. \end{align*}$$

These towers have ramification invariant $7$ , and the corresponding levels of each tower have the same genus. Table 1 shows they do not have identical a-numbers, although the a-numbers are highly constrained.

Table 1 Basic towers with $p=3$ and $d=7$ , five levels.

In particular, letting $\mathcal {T}$ be any of these three towers, we observe that for $1 \leq n \leq 5$ ,

(4.3) $$ \begin{align} a(\mathcal{T}(n)) = 7 \alpha(3) (3^{2n}- 9) + a(\mathcal{T}(1)) = \frac{7}{24} (3^{2n}- 9) + a(\mathcal{T}(1)). \end{align} $$

This holds for all of levels of all basic towers in characteristic $3$ with ramification invariant $7$ that we have computed. (In total, we computed the a-number of the first five levels of $4$ towers and of the first four levels of $16$ towers.) Note that by [BC1, Th. 6.26], $3 \leq a(\mathcal {T}(1)) \leq 4$ for any ${\mathbf Z}_3$ -tower with ramification invariant $7$ .

Example 4.3. Let $p=3$ and $d=5$ . Consider the basic towers

$$\begin{align*}\mathcal{T}_1 : Fy - y = [x^{5}] - [x^{2}] \quad \text{and} \quad \mathcal{T}_2 : Fy - y = [x^{5}] - [x^{4}] - [x]. \end{align*}$$

Table 2 shows that unlike for towers with ramification invariant $7$ , the a-number of the first level does not determine the a-number of higher levels for $\mathcal {T}_1$ and $\mathcal {T}_2$ .

Table 2 Basic towers with $p=3$ and $d=5$ , five levels.

For $n \geq 2$ , it appears that

$$\begin{align*}a(\mathcal{T}_1(n)) = \frac{5}{24} (3^{2n} - 9) + 4 \quad \text{and} \quad a(\mathcal{T}_2(n)) = \frac{5}{24} (3^{2n} - 9) + 3. \end{align*}$$

These formulae are not valid for $n=1$ . In particular, this illustrates that the restriction that n is sufficiently large in Conjecture 4.1 is necessary. Based on our computations with $13$ towers (some with only four levels computed), it appears that we may take $N_5 = 2$ . Furthermore, note that by [BC1, Th. 6.26], $a(\mathcal {T}(1))=2$ for any basic ${\mathbf Z}_3$ -tower $\mathcal {T}$ with ramification invariant $5$ .

Example 4.4. Table 3 shows the a-numbers of five selected basic ${\mathbf Z}_3$ -towers with ramification invariant $23$ . The tower $\mathcal {T}_1$ is $Fy - y = [x^{23}]$ , whereas the other four towers are more complicated. ⁵ For example, $\mathcal {T}_2$ is

$$\begin{align*}Fy - y = [x^{23}] +[x^{20}] +[x^{17}] +[x^{16}] +[x^{14}] -[x^{13}] -[x^{10}] -[x^{8}] -[x^{7}] -[x^{5}] +[x^{2}] +[x]. \end{align*}$$

Table 3 Basic towers with $p=3$ and $d=23$ .

We see the same basic phenomena as in Examples 4.2 and 4.3, although the stabilization is now more complicated. It appears that $\delta _{23}(\mathcal {T}(n))$ may not stabilize until the third level, there are multiple choices for the a-number of level 1, and $\delta _{23}(\mathcal {T}(n))$ may jump multiple times. Still, all of our examples are consistent with Conjecture 4.1 holding with $N_{23}= 3$ .

Remark 4.5. For basic ${\mathbf Z}_3$ -towers, computing the a-number of the fifth level is pushing the limit of what is feasible to compute as illustrated by Example 4.4. As the genus is growing exponentially with n, computing with the sixth level would require more time and memory than is reasonable. ⁶

4.2 Evidence in characteristic 3

In total, we have computed the a-number for the first four or five levels of at least $243$ basic ${\mathbf Z}_3$ -towers. ⁷ The largest ramification invariant d with which we have computed is $d=49$ , and most of the computations of the fifth level of ${\mathbf Z}_3$ -towers have taken place either for the tower $F y = y = [x^d]$ or with d relatively small. The computations take increasing amounts of time for larger d as the genus of the nth level depends linearly on d and the running time is polynomial in the genus. For larger d, we analyzed five levels for the tower $Fy - y = [x^d]$ for d up to $49$ ; as discussed in Remark 7.11, this tower is quicker to compute with. ⁸

We also computed the first three levels of $510$ towers with ramification invariant up to 30, ⁹ carefully chosen so as to have diversity of a-numbers for the first level. For each d, we searched through a large number of polynomials $f \in \mathbf F_3[x]$ of degree d and computed the a-number of the Artin–Schreier curve

$$\begin{align*}C_f : y^3 -y = f(x). \end{align*}$$

For each value $\alpha $ of the a-number appearing frequently, we picked $10$ polynomials $f = \sum _{i=0}^d c_i x^i$ (with $c_d \neq 0$ and $c_i=0$ when $p \mid i$ ) such that $a(C_f) = \alpha $ and computed the a-numbers for the first three levels of the Artin–Schreier–Witt tower

$$\begin{align*}\mathcal{T}_f: Fy - y = \sum_{i=0}^d [c_i x^i] \end{align*}$$

whose first level is $C_f$ .

Definition 4.6. An integer $n>1$ is a discrepancy of a basic tower $\mathcal {T}$ with ramification invariant d if $\delta _d(\mathcal {T}(n)) \neq \delta _d(\mathcal {T}(n-1))$ , where $\delta _d$ is as in (4.2).

Conjecture 4.1 is equivalent to the assertion that for each d, the largest discrepancy for a basic tower with ramification invariant d is bounded independently of the tower. If the conjecture holds, for n sufficiently large $\delta _d(\mathcal {T}(n)) $ would be the constant term c.

Table 4 shows the discrepancies for all of the towers we have collected data on with $d<50$ as well as the number of towers we analyzed for each d. (For small values of d, it is essential to work over extensions of $\mathbf F_3$ as there are not that many basic towers defined over $\mathbf F_3$ .) This table supports Conjecture 4.1 as it suggests that the discrepancies for towers with a given ramification invariant are bounded; the first time $n=2$ is a discrepancy is for $d=5$ , the first time $n=3$ is a discrepancy is for $d=11$ , and the first time $n=4$ is a discrepancy is for $d=29$ . In particular, we expect that for each basic ${\mathbf Z}_3$ -tower with ramification invariant d, there exists $c \in {\mathbf Z}$ such that

$$\begin{align*}a(\mathcal{T}(n)) = \alpha(3) d (3^{2n} -9) + c \quad \text{for} \ n \gg 0, \end{align*}$$

with the threshold for “ $n \gg 0$ ” growing slowly with d.

Table 4 Observed discrepancies for basic towers with ramification invariant $d<50$ .

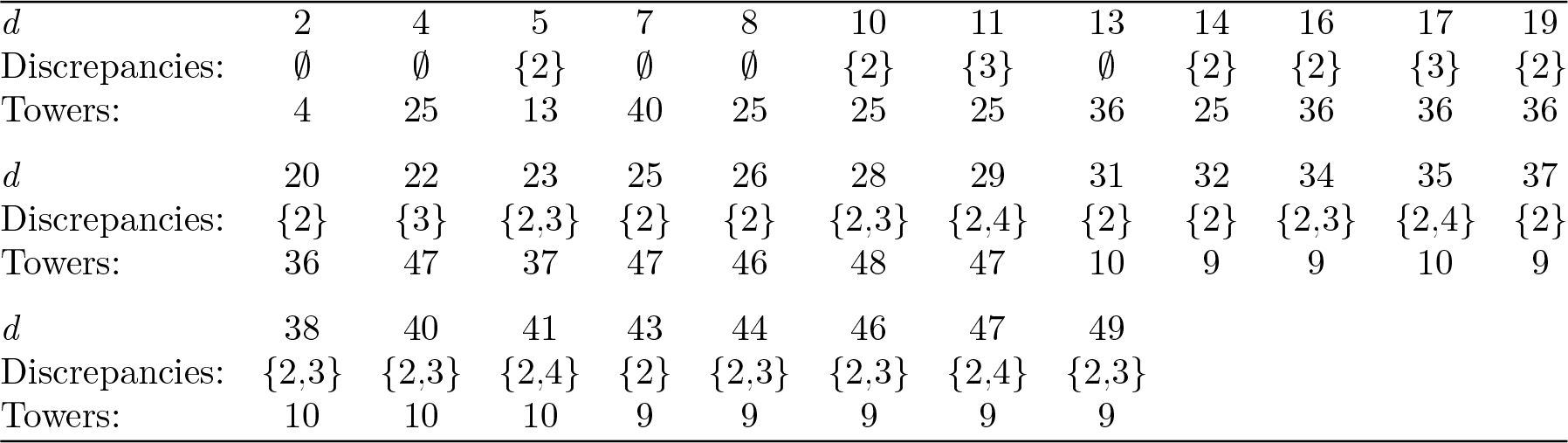
Remark 4.7.

1. 1. As described above, we have looked at fewer examples with $30 < d < 50$ , so are less confident that we have identified all of the discrepancies possible for basic towers with that ramification invariant.

2. 2. In all of the examples we have looked at, $| \delta _d(\mathcal {T}(n)) - \delta _d(\mathcal {T}(n+1))| \leq 4 $ .

3. 3. As we have very few examples of computations with five levels and large d, and no computations in level 6, it is difficult to be confident that the a-numbers for towers that have a discrepancy at level $n=4$ actually stabilize. For example, while the data in Table 5 suggest that $\delta _{35}(\mathcal {T}'(n))$ might stabilize for $n\geq 4$ , we have no direct evidence that $\delta _{35}(\mathcal {T}'(n))=18$ for $n \geq 4$ . However, we do see that for small d (where the computations are fastest), the discrepancies (when there are any) are all very small, and only gradually increase as d increases, which we find to be convincing evidence that all basic towers satisfy Conjecture 4.1 for sufficiently large $N_d$ .

   Table 5 $\mathcal {T}: Fy-y=[x^{35}]$ , $\mathcal {T}'$ also has ramification invariant $35$ , $p=3$ .

   

4.3 Characteristic 2

We now briefly discuss the a-numbers of ${\mathbf Z}_2$ -towers in characteristic 2. Note that $\alpha (2) d = d/24$ . Table 6 gives a representative example; it shows the a-numbers for any basic ${\mathbf Z}_2$ -tower with ramification invariant $7$ .

Table 6 $\mathcal {T}$ is any basic ${\mathbf Z}_2$ -tower with ramification invariant $7$ , seven levels.

This is compatible with Conjecture 4.1. In fact, for every positive odd integer d, the a-numbers of all basic towers with ramification invariant d appear to be the same, and to support Conjecture 4.1. We are able to prove this: Corollary 8.12 shows that for any odd d and all $n>1$ ,

$$ \begin{align*} a(\mathcal{T}(n)) = \frac{d}{24}( 2^{2n} - 4) + a(\mathcal{T}(1)) - \frac{1}{2} = \frac{d}{6} (2^{2(n-1)}-1) + a(\mathcal{T}(1)) - \frac{1}{2}. \end{align*} $$

4.4 Other characteristics

Basic ${\mathbf Z}_p$ -towers for $p>3$ are more difficult to compute with as the curves involved are of even higher genus. (Recall that the genus of the nth level of a ${\mathbf Z}_p$ -tower with ramification invariant d is on the order of $d p^{2n}$ by Lemma 2.13.) We have only done substantial computations with a few simple towers in characteristic $5$ .

Example 4.8. Table 7 shows the a-numbers of the first four levels of the ${\mathbf Z}_5$ -towers $\mathcal {T}_d : Fy - y = [x^d]$ for small d. All of these towers support Conjecture 4.1 as $\delta _d(\mathcal {T}_d(n))$ appears to be eventually constant. To give context, $g(\mathcal {T}_{12}(4)) = 390,312$ and computing the a-number of $\mathcal {T}_{12}(4)$ using the methods of §7 took around 253 hours, whereas $g(\mathcal {T}_3(4)) = 97,344$ and computing the a-number of $\mathcal {T}_3(4)$ “only” took 8.5 hours.

Table 7 $\mathcal {T}_d : Fy-y=[x^d]$ with $3 \leq d \leq 12$ , four levels, $p=5$ .

Example 4.9. As ${\mathbf Z}_p$ -towers with $p>5$ are much slower to compute with, we have only been able to compute with the first two levels. This is not enough to address Conjecture 4.1, but is enough to provide evidence for the leading term by computing

(4.4) $$ \begin{align} \left| \frac{a(\mathcal{T}(2))} { \alpha(p) d p^{4} } -1 \right|. \end{align} $$

We expect it to be close to zero.

• • When $p=7$ , we computed the a-number for the second level of slightly over 1,000 ${\mathbf Z}_7$ -towers; this quantity was less than $.015$ for all of them.

• • When $p=11$ , we computed the a-number for the second level of around 650 ${\mathbf Z}_{11}$ -towers; this quantity was less than $.0053$ for all of them.

• • When $p=13$ , we computed the a-number for the second level of 11 ${\mathbf Z}_{13}$ -towers; this quantity was less than $.0051$ for all of them.

Approximating the leading term using just the second level in fact works better for larger p. For example, when just looking at the second level, there are ${\mathbf Z}_3$ -towers with (4.4) larger than $0.12$ . Of course, for those ${\mathbf Z}_3$ -towers, we have computed many more levels which support the conjectured leading term much better.

5 Further invariants for basic towers

We now investigate $a^{r}(\mathcal {T}(n))$ for basic ${\mathbf Z}_p$ -towers when $r>1$ . We begin with a more precise version of Conjecture 3.8 for basic ${\mathbf Z}_p$ -towers which is a refinement of Conjecture 1.2.

Notation 5.1. For fixed r and p, write the rational number $\alpha (r,p) = \frac {r (p-1)}{2 (p+1) ( (p-1) r + (p+1))}$ from Notation 3.3 in lowest terms, and let D be its denominator. Let $D'$ be the maximal divisor of D which is prime to p. When $D'>1$ (i.e., D is not a power of p), we define $m(r,p)$ to be the multiplicative order of $p^2$ modulo $D'$ . In the edge case that $D'=1$ , we set $m(r,p)=0$ .

Conjecture 5.2. Fix a prime p and positive integers d and r. If $m(r,p) =1$ , then there exists a positive integer $N_{d,r}$ such that for any basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d, there exists a rational number $c \in \mathbf {Q}$ such that

$$\begin{align*}a^{r}(\mathcal{T}(n)) = \alpha(r,p) d p^{2n} + c \quad \text{ for } n \geq N_{d,r}. \end{align*}$$

If $m(r,p)> 1$ , then there exists a positive integer $N_{d,r}$ and $\lambda _{d,r}\in \mathbf {Q}$ such that for any basic ${\mathbf Z}_p$ -tower $\mathcal {T}$ with ramification invariant d, there exists a function $c : {\mathbf Z}/m(r,p) {\mathbf Z} \to {\mathbf Q}$ such that

$$\begin{align*}a^{r}(\mathcal{T}(n)) = \alpha(r,p)d p^{2n} + c(n) + \lambda_{d,r} \cdot n \quad \text{ for } n \geq N_{d,r}. \end{align*}$$

Note that the denominator of $\alpha (1,p)$ is $4 (p+1) p$ , and hence $m(1,p)=1$ for any prime p. Thus, this conjecture is compatible with Conjecture 4.1.

Remark 5.3. The definition of $m(r,p)$ is natural as $a^{r}(\mathcal {T}(n))$ must be an integer, whereas $\alpha (r,p)d p^{2n}$ is often not an integer. With D as in Notation 5.1, for n sufficiently large, the congruence class of $p^{2n}$ modulo D depends only on n modulo $m(r,p)$ . To obtain an integer prediction for $a^{r}(\mathcal {T}(n))$ in the conjecture, it is therefore natural to expect a formula depending on n modulo $m(r,p)$ .

When $m(r,p)=0$ (i.e., $D'=1$ ), we still expect $a^{r}(\mathcal {T}(n))$ to be of the form $\alpha (r,p)d p^{2n} + c(n) + \lambda \cdot n $ with $c(n)$ a function with period $m \geq 1$ . However, we do not make any prediction for the period. In these cases, it seems that $\lambda $ and m may depend more subtly on the tower, rather than just on $d,p$ , and r (see Example 5.9).

For convenience, while testing this conjecture, for a ${\mathbf Z}_p$ -tower $\mathcal {T}$ and rational number, $\lambda $ we define

(5.1) $$ \begin{align} \delta_{d,r}(\mathcal{T}(n) , \lambda) := a^{r}(\mathcal{T}(n)) - \left( \alpha(r,p) d p^{2n} + \lambda n \right) \end{align} $$

(cf. equation (4.2)). Analogously, we define the following definition.

Definition 5.4. An integer $n>m(r,p)$ is a discrepancy of a basic tower $\mathcal {T}$ with ramification invariant d for the rth power of the Cartier operator if

$$ \begin{align*} \delta_{d,r}(\mathcal{T}(n),\lambda_{d,r}) \neq \delta_{d,r}(\mathcal{T}(n-m(r,p)),\lambda_{d,r}). \end{align*} $$

Conjecture 5.2 is equivalent to $\delta _{d,r}(\mathcal {T}(n), \lambda _{d,r})$ being eventually periodic with period $m(r,p)$ (for an appropriate choice of $\lambda _{d,r}$ ). Equivalently, the largest discrepancy with respect to the rth power of the Cartier operator for towers with ramification invariant d should be bounded independently of the tower.

5.1 Characteristic 2 examples

Because the constant term in our conjectured formula will often depend on the congruence class of n modulo $m(r,p)$ , the best evidence for this conjecture comes from characteristic 2, where it is feasible to compute with more levels of the towers. While we have been able to prove an exact formula for $a^{r}(\mathcal {T}(n))$ in characteristic $p=2$ when $r=1$ (for all n) in Corollary 8.12, we have been unable to generalize this result to larger values of r. As such, the evidence we collect below is necessarily computational in nature.

Example 5.5. We begin by considering two basic ${\mathbf Z}_2$ -towers with ramification invariant $21$ . Tables 8 and 9 show the genus and the dimension of the kernel for the first 10 powers of the Cartier operator for the first seven levels of these two towers. We see that $a(\mathcal {T}(n)) = a(\mathcal {T}'(n))$ for all $1 \leq n \leq 7$ , and we see that $a^r(\mathcal {T}(1)) = a^r(\mathcal {T}'(1))$ for $1 \leq r \leq 10$ , which we prove in Corollary 8.12 and Lemma 8.16(1). Beyond that, $a^r(\mathcal {T}(n))$ will depend on the tower $\mathcal {T}$ . For example, $a^{2}(\mathcal {T}(3)) = 94 \neq a^{2}(\mathcal {T}'(3)) = 95$ and $a^{3}(\mathcal {T}(2)) = 31 \neq a^{3}(\mathcal {T}'(2)) = 33$ .

Table 8 $\mathcal {T}: Fy-y=[x^{21}] +[x^{19}] +[x^{15}] +[x^{13}] +[x^{9}]$ with $(p,d) = (2,21)$ .

Table 9 $\mathcal {T}' : Fy-y=[x^{21}] +[x^{13}] +[x^{9}] +[x^{5}] +[x^{3}]$ with $(p,d) = (2,21)$ .

Table 10 shows $21 \alpha (r,2)$ and $m(r,2)$ for $1 \leq r \leq 10$ . Our computations with the first seven levels of $\mathcal {T}$ and $\mathcal {T}'$ support Conjecture 5.2. For example, we see that for $1 < n \leq 7$ ,

$$\begin{align*}a^{2}(\mathcal{T}(n)) = \begin{cases} \frac{7}{5}( 2^{2n}+1) + n, & n \text{ odd,} \\ \frac{7}{5} ( 2^{2n}-1) +n +2, & n \text{ even,} \end{cases} \quad a^{2}(\mathcal{T}'(n)) = \begin{cases} \frac{7}{5}( 2^{2n}+1) + n +1, & n \text{ odd,} \\ \frac{7}{5} ( 2^{2n}-1) +n +2, & n \text{ even.} \end{cases} \end{align*}$$

Note that $m(2,2)=2$ as expected. Likewise, for $2< n \leq 7$ ,

$$\begin{align*}a^{3}(\mathcal{T}(n)) = \frac{7}{4} \cdot 2^{2n} + 4, \quad a^{3}(\mathcal{T}'(n)) = \frac{7}{4} 2^{2n} + 5. \end{align*}$$

Furthermore,

$$\begin{align*}a^{4}(\mathcal{T}(n)) = \begin{cases}\! 2 \cdot 2^{2n} + n, & {n \equiv 0\ \pmod{3},} \\ 2 \cdot 2^{2n} + n + 1, & n \equiv 1\ \pmod{3}, \\ 2 \cdot 2^{2n} + n + 2, & n \equiv 2\ \pmod{3}, \\ \end{cases} \!\quad a^{4}(\mathcal{T}'(n)) = \begin{cases}\! 2 \cdot 2^{2n} + n, & {n \equiv 0\ \pmod{3},} \\ 2 \cdot 2^{2n} + n + 3, & n \equiv 1\ \pmod{3}, \\ 2 \cdot 2^{2n} + n + 4, & n \equiv 2\ \pmod{3}, \\ \end{cases} \end{align*}$$

with $1 <n \leq 7$ for $\mathcal {T}$ and $2 < n \leq 7$ for $\mathcal {T}'$ . Considering the fifth power, for $2 < n \leq 7$ ,

$$\begin{align*}a^{5}(\mathcal{T}(n)) = a^{5}(\mathcal{T}'(n)) = \frac{35}{16} 2^{2n} + 2. \end{align*}$$

There appear to be similar formulas with $\lambda =1$ for $a^{r}(\mathcal {T}(n))$ depending on n modulo $3$ for $r = 6$ and depending on n modulo $2$ for $r=7$ . These are all compatible with Conjecture 5.2. There are not obvious formulas of a similar nature when $r=8$ or $r=10$ , but our conjecture predicts that the formulas would depend on n modulo $5$ or $6$ . With only seven levels of the tower and with the invariants taking a couple of levels to stabilize, we would not expect to see periodic behavior. When $r=8$ and $r=10$ , the dimensions are quite close to $\alpha (r,p) d p^{2n}$ as expected. When $r=9$ , as the denominator of $\alpha (9,2) = 21/8$ is a power of 2, we do not make a prediction for the period. It appears that the period is 1, as for $4 \leq n \leq 7$ ,

$$\begin{align*}a^{9}(\mathcal{T}(n)) = \frac{21}{8} 2^{2n} + 8, \quad a^{9}(\mathcal{T}'(n)) = \frac{21}{8} 2^{2n} + 11. \end{align*}$$

Table 10 Constants for $(p,d) = (2,21)$ .

Example 5.6. Consider the ${\mathbf Z}_2$ -towers $\mathcal {T}: Fy - y = [x^9] + [x^3] + [x]$ and $\mathcal {T}': Fy - y = [x^9] + [x]$ . It appears that $\lambda _{9,2} = 1/2 $ , $\lambda _{9,4} = 1/3$ , and $\lambda _{9,7} = 1/2$ . Table 11 shows some selected values of $\delta _{d,r}(\mathcal {T}(n),\lambda _{d,r})$ and $\delta _{d,r}(\mathcal {T}'(n),\lambda _{d,r})$ . These all support Conjecture 5.2, which predicts that the tower will have period $2$ (resp. $3$ , $2$ ) when $r=2$ (resp. $4$ , $7$ ). However, there are now larger discrepancies. For example, it looks as if $a^2(\mathcal {T}(n)) = a^2(\mathcal {T}'(n)) = 3\cdot 2^{2n}/5 + n/2 + c(n)$ where $c(n) = 1/10$ if n is odd and $c(n) = -3/5$ if n is even, except for $n=2,3$ .

Table 11 “Constant terms” for $\mathcal {T}$ and $\mathcal {T}'$ , $(p,d) = (2,9)$ .

Example 5.7. The tower $Fy - y = [x^3]$ is simple enough that we have been able to compute with the eighth level, allowing us to see some slightly longer periods. When $r=8$ (resp. $r=10$ ), observe that $m(r,2) = 5$ (resp. $m(r,2)=6$ ). Table 12 shows the beginnings of periodic behavior of the expected period. This example is quite simple as the ramification invariant is so small; we estimate that $\lambda _{3,r}=0$ and the low levels of the tower do not appear to have any irregularities relative to the rest of the tower.

Table 12 “Constant terms” for $Fy - y = [x^3]$ , $p=2$ .

Example 5.8. When r is large, it is difficult to test Conjecture 5.2 as $m(r,p)$ is often too big to see periodic behavior given the number of levels we are able to compute. Furthermore, as $V_{\mathcal {T}(n)}$ is nilpotent, for any fixed n, the genus of $\mathcal {T}(n)$ is equal to $a^{r}(\mathcal {T}(n))$ for r sufficiently large, which means that we would need additional levels to see the behavior for large powers of the Cartier operator.

Consider the ${\mathbf Z}_2$ -towers

$$ \begin{align*} \mathcal{T} &: Fy - y = [x^{19}] + [x^{17}] + [x^{13}] + [x^5] + [x^3], \\ \mathcal{T}' &: Fy - y = [x^{19}] + [x^{17}] + [x^{15}] + [x^{11}] + [x^9] + [x^7] + [x^5] + [x]. \end{align*} $$

We computed $a^{r}(\mathcal {T}(n))$ for $r \leq 200$ and $n \leq 7$ . For $r=13$ and $r=17$ , we see the expected behavior with periods $1$ and $2$ as predicted. On the other hand, for $r=125$ , our conjecture predicts the period to be 1, but we cannot see this; $\delta _{19,125}(\mathcal {T}(n),0)$ and $\delta _{19,125}(\mathcal {T}'(n),0)$ do not appear to be constant. However, this is not so surprising as for $n \leq 5$ we have that $a^{125}(\mathcal {T}(n)) = g(\mathcal {T}(n))$ and likewise for $\mathcal {T}'$ . It is only for larger values of n that we would expect to see the finer behavior of $a^{125}(\mathcal {T}(n))$ , and computing with $n \leq 7$ only gives two “interesting” levels.

Example 5.9. Our conjecture does not predict the period in the edge case that $m(r,2) =0$ ; this case appears more subtle. For example, $\alpha (9,2) = 1/8 $ and hence $m(9,2)=0$ , while Table 13 shows that $\delta _{19,9}(\mathcal {T}(n),0) = a^{9}(\mathcal {T}(n)) - 19 \cdot 2^{2n-3}$ for the two towers with ramification invariant $19$ in Example 5.8. It looks like the tower $\mathcal {T}$ has period 1 and $\lambda =0$ , whereas $\mathcal {T}'$ has period 2 with $\lambda =1/2$ .

Table 13 “Constant terms” for $\mathcal {T}$ and $\mathcal {T}'$ , $(p,d) = (2,19)$ .

We have systematically tested Conjecture 5.2 against a collection of at least $221$ basic ${\mathbf Z}_2$ -towers where we analyzed at least five levels. (We analyzed seven levels for $55$ of them.) For each ramification invariant d, we picked one tower $\mathcal {T}_0$ where we had computed seven levels and used it to estimate $\lambda _{d,r}$ by computing ¹⁰

$$\begin{align*}\frac{\left( a^{r}(\mathcal{T}_0(7)) - \alpha(r,p) d p^{14} \right) - \left( a^{r}(\mathcal{T}_0(7-m(r,p))) - \alpha(r,p) d p^{2(7-m(r,p))} \right)}{m(r,p)}. \end{align*}$$

If Conjecture 5.2 held for $n \geq 7 - m(r,p)$ , this ratio would equal $\lambda _{d,r}$ . Furthermore, if Conjecture 5.2 holds and we have the correct $\lambda _{d,r}$ , for n large enough, $\delta _{d,r}(\mathcal {T}(n),\lambda _{d,r})$ would equal $c(n)$ .

Tables 14–16 show the discrepancies we have found in our database for $d<24$ and $r=2,3,4$ . Table 14 shows the number of towers under consideration with each ramification invariant. Note that the smallest possible discrepancy is $m(r,2)+1$ , so is $3$ when $r=2$ , $2$ when $r=3$ , and $4$ when $r=4$ . These tables support Conjecture 5.2 as the discrepancies appear to only occur for relatively small n ( $7$ is the largest potential discrepancy we would see using our data). When $r=5$ (and $m(r,2)=1$ ), we only see discrepancies at levels 2 and 3.

Table 14 Some observed discrepancies for basic ${\mathbf Z}_2$ -towers, $r=2$ .

Table 15 Some observed discrepancies for basic ${\mathbf Z}_2$ -towers, $r=3$ .

Table 16 Some observed discrepancies for basic ${\mathbf Z}_2$ -towers, $r=4$ .

Remark 5.10. In all of the examples we have computed, $| \delta _{d,r}(\mathcal {T}(n) , \lambda _{d,r}) - \delta _{d,r}(\mathcal {T}(n+1), \lambda _{d,r})| \leq 1 $ when $r=2$ (resp. $\leq 3$ when $r=3$ and $\leq 2$ when $r=4$ ).

5.2 Characteristic 3

Now, let $p=3$ . The evidence for Conjecture 5.2 is a bit weaker in characteristic 3 as our computations are limited to at most five levels.

Example 5.11. We begin by considering two basic ${\mathbf Z}_3$ -towers with ramification invariant $5$ . Tables 17 and 18 show the genus and the dimension of the kernel of the first 10 powers of the Cartier operator for the first five levels of these two towers. Table 19 shows $5 \alpha (r,3) $ and $m(r,3)$ . These examples support Conjecture 5.2.

Table 17 $\mathcal {T}: Fy-y=[x^{5}] +[2x^{2}]$ with $(p,d) = (3,5)$ .

Table 18 $\mathcal {T}' : Fy-y=[x^{5}] +[2x^{4}] +[2x]$ with $(p,d) = (3,5)$ .

Table 19 Constants for $(p,d) = (3,5)$ .

For $1 < n \leq 5$ , observe that

$$\begin{align*}a^{2}(\mathcal{T}(n)) = a^{2}(\mathcal{T}'(n)) = \begin{cases} \frac{5}{16} ( 3^{2n} -9) + \frac{n-1}{2} + 4, & n \text{ odd,} \\ \frac{5}{16} ( 3^{2n} -1) + \frac{n}{2} , & n \text{ even,} \end{cases} \end{align*}$$

whereas $m(2,3) = 2$ as expected. Similarly, for $1 < n \leq 5$ , we see

$$\begin{align*}a^{3}(\mathcal{T}(n)) = a^{3}(\mathcal{T}'(n)) = \begin{cases} \frac{3}{8} ( 3^{2n} -1) + 2, & n \text{ odd,} \\ \frac{3}{8} ( 3^{2n} -1) + 1, & n \text{ even.} \end{cases} \end{align*}$$

Furthermore, for $1 < n \leq 5$ , we have

$$\begin{align*}a^{4}(\mathcal{T}(n)) = a^{4}(\mathcal{T}'(n)) = \frac{5}{12} (3^{2n}-9) +5. \end{align*}$$

We expect $a^{5}(\mathcal {T}(n))$ to depend on n modulo $3$ , and one might optimistically conjecture that for $n \geq 1$ ,

$$\begin{align*}a^{5}(\mathcal{T}(n)) = a^{5}(\mathcal{T}'(n)) = \begin{cases} \frac{25}{56} ( 3^{2n} - 9) + \frac{n-1}{3} + 4, & n \equiv 1\ \pmod{3}, \\ \frac{25}{56} ( 3^{2n} - 25) + \frac{n-2}{3} + 14, & n \equiv 2\ \pmod{3}, \\ \frac{25}{56} ( 3^{2n} - 1) + \frac{n}{3}, & n \equiv 0\ \pmod{3}. \\ \end{cases} \end{align*}$$

This is consistent with our data, but is weaker evidence for Conjecture 5.2, as there is only one multiple of 3 for which we have computed with $\mathcal {T}(n)$ . As we have chosen the constant term of the $n \equiv 0\ \pmod {3}$ case so that $a^{5}(\mathcal {T}(3))$ is correct, that case is somewhat vacuous.

It is somewhat of a coincidence that $a^{r}(\mathcal {T}(n)) = a^{r}(\mathcal {T}'(n))$ for $r = 2,3,4,5$ . These are not equal when $r=1$ , or when $r=7$ where we find

$$\begin{align*}a^{7}(\mathcal{T}(n)) = \frac{35}{72} (3^{2n} -9^2) + 47 \quad\text{and}\quad a^{7}(\mathcal{T}'(n)) = \frac{35}{72} (3^{2n} -9^2) + 45, \end{align*}$$

for $3 \leq n \leq 5$ . When $r=10$ , we see a similar formula with the correct leading term, $\lambda =1/2$ , and period $2$ . When $r=8$ , observe that for $n=4,5$ ,

$$\begin{align*}a^{8}(\mathcal{T}(n)) = a^{8}(\mathcal{T}'(n)) = 3^{2n}/2 + 1/2. \end{align*}$$

This suggests that the $a^{8}(\mathcal {T}(n))$ may have period 1, while the predicted period is $m(8,3)=2$ . (This does not contradict Conjecture 5.2, as any function $c: {\mathbf Z}/m{\mathbf Z}\rightarrow {\mathbf Q}$ may be considered as a function on ${\mathbf Z}/m\ell {\mathbf Z}$ for each positive integer $\ell $ .) There are no obvious periodic formulas when $r=6$ or $r=9$ , but our conjecture predicts that these would depend on n modulo $4$ or $5$ , so with only five levels of the tower, we cannot expect to witness periodic behavior. In these cases, the dimensions are quite close to $\alpha (r,3) \cdot d \cdot 3^{2n}$ as expected.

We can systematically test Conjecture 5.2 against the collection of basic ${\mathbf Z}_3$ -towers described in §4.2 where we had computed invariants for four or five levels. For most of these towers, we computed with the first five powers of the Cartier operator. (The unusual case that $m(r,3) =0$ does not occur for $r < 5$ .) For fixed d and r, we used one of the towers $\mathcal {T}$ where we had computed five levels (often $Fy - y = x^d$ ) to predict $\lambda _{d,r}$ by computing

$$\begin{align*}\frac{\left( a^{r}(\mathcal{T}(5)) - \alpha(r,p) d p^{10} \right) - \left( a^{r}(\mathcal{T}(5-m(r,p))) - \alpha(r,p) d p^{2(5-m(r,p))} \right)}{m(r,p)}. \end{align*}$$

If Conjecture 5.2 holds for $\mathcal {T}(n)$ with $n \geq 5 - m(r,p)> N_d$ , this ratio is precisely $\lambda _{d,r}$ .

Using this prediction for $\lambda _{d,r}$ , Table 20 shows all the discrepancies (recall Definition 5.4) with $r=4$ and $d<30$ , and supports Conjecture 5.2. Note that in this situation $m(r,3)=1$ .

Table 20 Observed discrepancies for basic ${\mathbf Z}_3$ -towers, $r=4$ .

Similarly, Tables 21 and 22 support Conjecture 5.2 in that the formulas in the conjecture depend on the parity of n. Note that it is not possible to have a discrepancy at level 2 in this situation as $m(r,3)>1$ .

Table 21 Observed discrepancies for basic ${\mathbf Z}_3$ -towers, $r=2$ .

Table 22 Observed discrepancies for basic ${\mathbf Z}_3$ -towers, $r=3$ .

Since $m(5,3)=3$ , we only consider the asymptotic behavior of $a^{5}(\mathcal {T}(n))$ as it is not feasible to spot patterns with period $3$ using only five levels. Out of all of the towers $\mathcal {T}$ we analyzed, the maximum value of

(5.2) $$ \begin{align} \left| \frac{a^{5}(\mathcal{T}(n))}{\alpha(r,3)\cdot d \cdot 3^{2n}} - 1\right| \end{align} $$

is less than $.0021$ for $n=3$ , less than $.0013$ for $n=4$ , and less than $.00024$ for $n=5$ . This supports Conjecture 3.4 and that we have the correct main term in Conjecture 5.2.

5.3 Other characteristics

For $p>3$ , our computations are necessarily more limited in scope. Nevertheless, we record several examples with $p>3$ below.

Example 5.12. When $p =5$ , we compute that $m(5,5) =2$ and $m(r,5)>2$ for $r =2,3,4$ . Thus, we focus first on the case that $r=5$ , where there is a hope of seeing periodic behavior with just four levels of a ${\mathbf Z}_5$ -tower. By eyeballing the towers $\mathcal {T}_d : Fy - y = x^d$ with $d \leq 12$ , it looks like $\lambda _{d,5} =0$ for $d < 7$ and $\lambda _{d,5} = 1/2$ for $7 \leq d \leq 12$ . Table 23 shows that $\delta _{d,5}(\mathcal {T}(n),\lambda _{d,5})$ appears to be periodic with period 2 (as expected) for these towers. This again supports Conjecture 5.2.

Table 23 $\mathcal {T}_d: Fy-y=[x^d]$ with $3 \leq d \leq 12$ , four levels.

For $r \in \{2,3,4\}$ , we can only meaningfully investigate the leading term. We computed

$$\begin{align*}\left| \frac{ a^{r}(\mathcal{T}(n))}{\alpha(r,5) d 5^{2n}} -1 \right| \end{align*}$$

for these towers: with $n=3$ , the maximum value was less than $.000273$ (resp. $.000266$ , $.0021$ ) when $r=2$ (resp. $r=3$ , $r=4$ ). For $n=4$ , the maximum value was less than $6.4 \cdot 10^{-5}$ (resp. $6.4 \cdot 10^{-5}$ , $9.5 \cdot 10^{-5}$ ) when $r=2$ (resp. $r=3$ , $r=4$ ).

Example 5.13. When $p>5$ , we were only able to compute with two levels. We computed

$$\begin{align*}\left| \frac{a^{r}(\mathcal{T}(2))}{\alpha(r,p) d p^4} - 1 \right| \end{align*}$$

for a variety of basic ${\mathbf Z}_p$ -towers with ramification invariant d.

• • When $p=7$ , we analyzed the second level of around 1,000 ${\mathbf Z}_7$ -towers. The above quantity was always less than $.02$ for $r \in \{2,3,4,5\}$ .

• • When $p=11$ , we analyzed the second level of around $650 \ {\mathbf Z}_{11}$ -towers. The above quantity was always less than $.003$ for $r \in \{2,3,4,5\}$ .

• • When $p=13$ , we analyzed the second level of 11 ${\mathbf Z}_{13}$ -towers. The above quantity was always less than $.0042$ for $r \in \{2,3,4,5\}$ .

Again, this supports the formula for the leading term in Conjecture 5.2.

6 Beyond basic towers

In §§4 and 5, we focused on basic ${\mathbf Z}_p$ -towers due to their simplicity. In this section, we provide computational evidence that Conjectures 3.4, 3.7, and 3.8 hold for other monodromy-stable towers, and provide evidence that Philosophy 1.1 holds for nonmonodromy-stable towers.

6.1 Monodromy-stable towers with the same ramification as basic towers

So far, we have focused on basic ${\mathbf Z}_p$ -towers as they have a particularly simple description using Artin–Schreier–Witt theory. Now, we consider more complicated ${\mathbf Z}_p$ -towers that are totally ramified over a single point and have the same ramification as a basic ${\mathbf Z}_p$ -tower. To do this, we pick basic ${\mathbf Z}_p$ -towers $\mathcal {T}_{\textrm {basic}} : Fy - y = \sum _{i=1}^d [c_i x^i]$ , and consider the related ${\mathbf Z}_p$ -towers

$$\begin{align*}\mathcal{T}_{\textrm{mod}} : Fy - y = \sum_{i=1}^d [c_i x^i] + \sum_{j=1}^{d-1} d_j p [x^j] = \sum_{i=1}^d (c_i x^i,0,0,\ldots) + \sum_{j=1}^{d-1}(0,d_j x^{jp},0,\ldots), \end{align*}$$

where we let $d_j $ be $0$ or $1$ at random when $p \nmid j$ (and $d_j=0$ when $p \mid j$ ). The first levels of these modified towers agree with that of the basic tower, whereas higher levels do not. However, by Fact 2.2, we know that they have the same ramification breaks above infinity (and are unramified elsewhere).

We did this extensively in characteristic $p=3$ , picking around $100$ basic towers with ramification invariants up to $19$ and considering 10 modifications of each. We computed $a^{r}(\mathcal {T}(n))$ for the first four levels of all of these towers and $1 \leq r \leq 10$ . The modified towers always supported Conjectures 3.4, 3.7, and 3.8. In fact, we almost always found that $a^{r}(\mathcal {T}_{\textrm {basic}}(n)) = a^{r}(\mathcal {T}_{\textrm {mod}}(n))$ . There were only some scattered examples where they differed, and only for $r=8$ .

6.2 Towers ramified over multiple points

We now consider monodromy-stable towers of curves which are totally ramified over multiple points. Because of the multiple points of ramification, we cannot use the program described in §7. As it is quite slow to compute examples without this program, we content ourselves with a couple of examples with a-numbers in characteristic $p=3$ and a general result in characteristic $p=2$ .

Example 6.1. Let $p=3$ , and consider the towers over $\mathbf {P}^1_{\mathbf F_p}$ defined by the Artin–Schreier–Witt equations

$$\begin{align*}\mathcal{T}: Fy - y = [x^5] + [x^{-5}] \quad \text{and} \quad \mathcal{T}' : Fy - y = [x^7] + [x^{-5}]. \end{align*}$$

Using Magma’s built-in functionality for computing a-numbers, we can compute the a-numbers of the first four levels of these towers. These are shown in Table 24, along with data for the the basic towers $\mathcal {T}_5$ and $\mathcal {T}_7$ given by $Fy- y = [x^5]$ and $Fy - y = [x^7]$ , respectively. We were unable to investigate higher levels as Magma’s built-in functionality for computing with the Cartier operator is much less efficient than the (inapplicable) methods of §7; for example, computing $a(\mathcal {T}'(4))$ took around 38 hours. (For reference, Section 7 includes a systematic comparisons of the running time of our algorithm and Magma’s default methods when they both apply.)

Table 24 Invariants of $\mathcal {T}$ , $\mathcal {T}', \mathcal {T}_5,$ and $\mathcal {T}_7$ , characteristic $3$ , levels $1$ – $4$ .

We have that $\alpha (3) = 1/24$ . For $2 \leq n \leq 4$ , notice that

$$ \begin{align*} a(\mathcal{T}) &= 5 \alpha(3) ( 3^{2n}-9) + 5 \alpha(3) ( 3^{2n}-9) + 6 = \frac{5}{12} 3^{2n} + \frac{9}{4}, \\ a(\mathcal{T}') &= 5 \alpha(3) (3^{2n}-9) + 7\alpha(3) (3^{2n}-9) + 8 = \frac{1}{2} 3^{2n} + \frac{7}{2}. \end{align*} $$

These support Conjectures 3.4 and 3.7. Note that the a-numbers for $\mathcal {T}$ and $\mathcal {T}'$ are almost a “sum” of the a-numbers of the basic towers: ¹¹ we see that for $2 \leq n \leq 4$ ,

$$\begin{align*}a(\mathcal{T}(n)) = a(\mathcal{T}_5(n)) + a(\mathcal{T}_5(n))-2 \quad \text{and} \quad a(\mathcal{T}'(n)) = a(\mathcal{T}_5(n)) + a(\mathcal{T}_7(n)). \end{align*}$$

This supports Philosophy 3.1, as each point of ramification makes a contribution to the a-number.

Example 6.2. Consider the Igusa tower $\operatorname {\mathrm {Ig}}$ in characteristic 3 as in Example 2.15. There are two supersingular points of $\operatorname {\mathrm {Ig}}(1) \simeq X_1(5)_k$ (this uses that $p=3$ ), so the tower given by $\mathcal {T}(n) := \operatorname {\mathrm {Ig}}(n+1)$ is totally ramified over two points and unramified elsewhere. The ramification invariant at level n above each of the points is $9^{n-1}-1$ . We know that the genus is

$$\begin{align*}g(\operatorname{\mathrm{Ig}}(n)) = 3 \cdot 3^{2(n-1)} - 4 \cdot 3^{n-1} +1. \end{align*}$$

Table 25 shows invariants of $\operatorname {\mathrm {Ig}}(n)$ for those small values of n where we could compute it. ¹² In particular, notice that it appears $a(\operatorname {\mathrm {Ig}}(n))= 3^{2(n-1)} - 1$ . Using Lemma 2.6, we see that nth break in the lower numbering filtration of $\mathcal {T}$ is $12 \cdot 3^{n-1} - 4$ above each of the ramified points. Then, as $12 \alpha (3) = 1/2$ , Conjecture 3.7 predicts that the a-number of $\operatorname {\mathrm {Ig}}(n) = \mathcal {T}(n-1) $ will be

$$\begin{align*}(12 + 12) \alpha(3) 3^{2(n-1)} + c = 3^{2(n-1)}+ c \text{ for } n \gg 0. \end{align*}$$

Our data for a-numbers therefore support Conjectures 3.4 and 3.7. Likewise, it appears that

$$\begin{align*}a^{2}(\operatorname{\mathrm{Ig}}(n)) = \frac{3}{2}\cdot 3^{2(n-1)} - \frac{3}{2} \end{align*}$$

in line with Conjectures 3.4 and 3.8. Similarly, for the third power, Conjecture 3.4 predicts that $a^{3}(\operatorname {\mathrm {Ig}}(n))$ is asymptotically $9/5 \cdot 3^{2(n-1)}$ . We compute that

$$\begin{align*}\frac{a^{3}(\operatorname{\mathrm{Ig}}(2))}{ 9/5 \cdot 3^2} \approx .864, \quad \text{and} \quad \frac{a^{3}(\operatorname{\mathrm{Ig}}(3))}{ 9/5 \cdot 3^4} \approx .988. \end{align*}$$

(Note that $\frac {9}{5}3^{2(n-1)}- \frac {9}{5} =a^{3}(\operatorname {\mathrm {Ig}}(n))$ for $n=1,3$ , but for $n=2$ this expression is not an integer. However, taking its floor gives $a^{3}(\operatorname {\mathrm {Ig}}(2))$ .) Again, these support Conjecture 3.4 for monodromy-stable towers with multiple points of ramification and reflect Philosophy 3.1.

Table 25 Invariants of $\operatorname {\mathrm {Ig}}(n)$ , characteristic $3$ , three levels.

To compute with this Igusa tower, we worked with the universal elliptic curve over $X_1(5)$

$$\begin{align*}E : y^2 + (1 + t)xy + ty = x^3 + tx^2. \end{align*}$$

(Obtaining this equation is a relatively standard calculation, e.g., carried out in [S3, §2.2].) To obtain the function field of $\operatorname {\mathrm {Ig}}(n)$ , we adjoin the kernel of the Verschiebung $V^{n} : E^{(p^n)} \to E$ to $\mathbf F_p(t)$ . We can obtain a formula for V from the multiplication by 3 map on E, and then iterate it (with appropriate Frobenius twists on coefficients) to obtain a polynomial with the coordinates of $\ker V^n$ as roots. Given this description of the function field of $\operatorname {\mathrm {Ig}}(n)$ , Magma can compute a basis for the regular differentials on $\operatorname {\mathrm {Ig}}(n)$ and a matrix for the Cartier operator with respect to this basis.

We can also prove that similar behavior for a-numbers in towers with multiple points of ramification happens in characteristic 2 under a technical hypothesis (see Corollary 8.10). Again, each point of ramification makes a contribution.

Example 6.3. Let $p=2$ , and consider the ${\mathbf Z}_2$ -towers $\mathcal {T}: F y - y = [x^ 3] + [x^{-3}] + [(x-1)^{-3}]$ and $\mathcal {T}' : Fy - y = [x^ 3] + [x] + [x^{-1}] + [(x-1)^{-5}]$ . These are towers over the projective line ramified over $0$ , $1$ , and $\infty $ . We have that $d_0(\mathcal {T}(n)) = d_{\infty }(\mathcal {T}(n)) = d_1(\mathcal {T}(n)) = d_0(\mathcal {T}'(n)) = 2^{2n-1}+1$ , that $d_1(\mathcal {T}'(n)) = \frac {5}{3} (2^{2n-1}+1)$ , and that $d_{\infty }(\mathcal {T}'(n)) = (2^{2n-1}+1)/3$ . Table 26 shows data for the first four levels of these towers. (As there are multiple points of ramification, we can only use magma’s slower generic methods, so look at fewer levels.) The a-numbers satisfy the formula (8.11) even though the technical hypothesis

$$\begin{align*}\sum_{Q \in S} (d_Q(\mathcal{T}(n))-1)/2 \geq 2 g(\mathcal{T}(n-1))-2 \end{align*}$$

is not satisfied for $n=4$ (and similarly for $\mathcal {T}'$ ).

Table 26 Tower over $\mathbf {P}^1$ ramified at three points, $p=2$ .

6.3 Towers over other bases

We now briefly discuss ${\mathbf Z}_p$ -towers whose base is not the projective line. A simple way to obtain such towers is to start with a ${\mathbf Z}_p$ -tower $\mathcal {T}$ over the projective line, and—for any fixed m—forget the first m levels of the tower to obtain a ${\mathbf Z}_p$ -tower over $\mathcal {T}(m)$ . It is worth pointing out that our conjectures are compatible with this procedure:

Lemma 6.4. Suppose that $\mathcal {T}$ is a monodromy-stable ${\mathbf Z}_p$ -tower totally ramified above a set S, and for a fixed integer $m \geq 1$ , let $\mathcal {T}'$ be the ${\mathbf Z}_p$ -tower $\cdots \to \mathcal {T}(m+1) \to \mathcal {T}(m)$ . Then $\mathcal {T}$ satisfies Conjecture 3.4 (resp. Conjecture 3.7 or 3.8) if and only if $\mathcal {T}'$ does.

Proof. This is essentially [KM2, Prop. 5.5], although we include a proof for the convenience of the reader. Note that $\mathcal {T}'$ is totally ramified ramified above a set $S'$ of points in $\mathcal {T}(m)$ , and for each $Q \in S$ , there is a unique point $Q' \in S'$ lying above it. As the Galois group of the tower $\mathcal {T}'$ is a subgroup of the Galois group of the tower $\mathcal {T}$ , we can directly compare the lower numbering filtrations. In particular, $d_Q(\mathcal {T}(n+m)) = d_{Q'}(\mathcal {T}'(n))$ .

Note that for a tower T ramified over Q, having $s_Q(T(n)) = d p^{n-1} + c$ for $n\gg 0$ is equivalent to $s_Q(T(n+1)) - s_Q(T(n)) = d (p-1)p^{n-1}$ for $n\gg 0$ . Using Lemma 2.6, we compute

$$ \begin{align*} s_{Q'}(\mathcal{T}'(n+1))) - s_{Q'}(\mathcal{T}'(n)) & = ( d_{Q'}(\mathcal{T}'(n+1)) - d_{Q'}(\mathcal{T}'(n))) p^{-n} \\ &= ( d_{Q}(\mathcal{T}(m+n+1)) - d_{Q}(\mathcal{T}(m+n))) p^{-n} \\ &= (s_{Q}(\mathcal{T}(m+n+1)) - s_Q(\mathcal{T}(m+n))) p^{m}. \end{align*} $$

Since $\mathcal {T}$ is monodromy-stable, there exists $d_Q \in {\mathbf Q}$ such that $s_Q(\mathcal {T}(m+n+1)) - s_Q(\mathcal {T}(m+n)) = d_Q (p-1) p^{n+m-1}$ for n large enough. Thus, we see that $s_{Q'}(\mathcal {T}'(n+1)) - s_{Q'}(\mathcal {T}'(n)) = d_Q p^{2m} (p-1) p^{n-1}$ for n large enough and hence $\mathcal {T}'$ is monodromy-stable. In particular, taking $d_{Q'} = d_Q p^{2m}$ , we have $s_Q(\mathcal {T}'(n))= d_{Q'} p^{n-1} + c_{Q'}$ for $n \gg 0$ .

Now, notice that

$$\begin{align*}\alpha(r,p) d_Q p^{2(n+m)}= \alpha( r,p) d_{Q'} p^{2n}; \end{align*}$$

the left side is the contribution of Q to the leading term of $a^{r}(\mathcal {T}(n+m))$ predicted by Conjecture 3.4, and the right side is the contribution of $Q'$ to $a^{r}(\mathcal {T}'(n))$ predicted by Conjecture 3.4. Thus, $\mathcal {T}$ satisfies Conjecture 3.4 if and only if $\mathcal {T}'$ does.

The implications for the other two conjectures follow from this and absorbing other terms involving m into the unspecified constants.

Investigating examples that do not arise in the above manner necessitates the use of Magma’s native functionality for computing with function fields, rather than the program described in §7 (which only works for ${\mathbf Z}_p$ -towers over the projective line). We must therefore limit ourselves to examples with $p=2$ in levels $n\le 5$ .

Example 6.5. Working in characteristic $p=2$ over $k=\mathbf F_2$ , we consider the three ${\mathbf Z}_2$ -towers over hyperelliptic ( $=$ Artin–Schreier over $\mathbf {P}^1_k$ ) curves given by

$$ \begin{align*} C_{1} &: y^2 - y = x-\frac{1}{x}-\frac{1}{x-1}, \quad & & \mathcal{T}_1 : Fz - z = [(x^2+x)y], \\ C_{2} &: y^2 - y = x^3-\frac{1}{x}, \quad & & \mathcal{T}_2: Fz - z = [xy], \\ C_{3} &: y^2 - y = x^5, \quad & & \mathcal{T}_3: Fz - z = [y]. \end{align*} $$

For $i=1,2,3$ , the curve $C_i$ is a genus $2$ branched ${\mathbf Z}/2{\mathbf Z}$ -cover of $\mathbf {P}^1_k$ , and $\mathcal {T}_i$ is a ${\mathbf Z}_2$ -tower, totally ramified over the unique point $Q_i$ on $C_i$ lying over $\infty $ on $\mathbf {P}^1_k$ , with (lower) ramification breaks

(6.1) $$ \begin{align} d_{Q_i}(\mathcal{T}_i(n))=5\cdot \frac{2^{2n - 1}+1}{3}. \end{align} $$

(Indeed, in each case, the function has an order $5$ pole at $Q_i$ and is regular elsewhere.) In particular,

(6.2) $$ \begin{align} g(\mathcal{T}_i(n)) = \frac{5\cdot 2^{2n-1} - 1}{3} + 3\cdot 2^{n-1}, \end{align} $$

for $i=1,2,3$ and all $n\ge 1$ . Note that $\mathcal {T}_i$ is not a ${\mathbf Z}_2$ -tower over $\mathbf {P}^1_k$ : one can check (using Magma or by hand ¹³ ) that the degree-4 cover $\mathcal {T}_i(1) \rightarrow \mathbf {P}^1_k$ is not Galois for $i=2,3$ , and is Galois with group ${\mathbf Z}/2{\mathbf Z} \times {\mathbf Z}/2{\mathbf Z}$ for $i=1$ . Table 27 summarizes some basic data about the $C_i$ . This represents all possible behaviors, as a result of Ekedahl [E1, Th. 1.1] shows that if $V=0$ on $H^0(C,\Omega ^1_{C/k})$ for a hyperelliptic curve C over a perfect field k of characteristic p, then $2g(C) \le p-1$ if $(g(C),p)\neq (1,2)$ ; in particular, there is no genus $2$ hyperelliptic curve in characteristic $p=2$ with a-number $2$ .

Table 27 Three genus $2$ hyperelliptic curves.

To investigate the behavior of $a^r(\mathcal {T}_i(n))$ for $i=1,2,3$ , we tabulate the differences

$$\begin{align*}\delta_{5,r}(\mathcal{T}_i(n),0)-c_r= a^r(\mathcal{T}_i(n)) - (\alpha(r,2)\cdot 5\cdot 2^{2n} + c_r) \quad\text{where}\quad c_r:=\begin{cases} 1/3, & \text{if}\ r=3, \\ 2/3, & \text{otherwise,} \end{cases} \end{align*}$$

and $\alpha (r,2) = \frac {r}{6(r+3)}$ is as in Notation 3.3; the constant term $c_r$ was selected to render most of the table entries integral.

If $m(r,p)$ is as in Notation 5.1, we have $m(r,2)=1$ if $r=1,3,5$ , whereas $m(2,2)=2$ and $m(4,2)=3$ . The facts that the $r=1,3,5$ columns in Table 28 appear to stabilize to constant functions, and the $r=2$ columns appear to be stabilizing to periodic functions with period $2$ (with possibly nonzero linear term $\lambda \cdot n$ when $i=2,3$ ), support Conjectures 3.4, 3.7, and 3.8, and suggest that a more precise variant of Conjecture 3.8 along the lines of Conjecture 5.2 should be true in this context as well. The $r=4$ columns appear to be less structured, but they are nonetheless consistent with Conjectures 3.4 and 3.8, and a possible analogue of Conjecture 5.2, which would predict a period of $m(4,2)=3$ that large relative to the modest number ( $n=5$ ) of levels we have been able to compute.

Table 28 Differences $a^r(\mathcal {T}_i(n)) - (\alpha (r,p)\cdot 5\cdot 2^{2n} + c_r)$ .

Remark 6.6. We note that the a-number formula (8.11) appears to hold for $\mathcal {T}_1(n)$ in all levels n, despite the fact that the technical hypothesis (8.10) does not hold: indeed, writing $d_n:=d_{Q_i}(\mathcal {T}_i(n))$ and $g_n:=g(\mathcal {T}_i(n))$ (noting that these numbers are independent of i by (6.1)–(6.2)), we compute

$$\begin{align*}\frac{d_{n+1} - 1}{2} - (2g_n - 2) = \frac{5\cdot 2^{2n} + 1}{3} - \frac{5\cdot 2^{2n}-2}{3} -3\cdot 2^n + 2 = 3(1-2^n), \end{align*}$$

which is negative for $n\ge 1$ . Note that as $\mathcal {T}_1(0)$ is ordinary, one knows a priori that the a-number of $\mathcal {T}_1(1)$ is given by (8.11) due to Remark 8.11. For $i=2,3$ , it appears that

$$\begin{align*}a(\mathcal{T}_i(n)) = a(\mathcal{T}_1(n)) + 2 \end{align*}$$

for all n (resp. all $n\ge 3$ ) when $i=3$ (resp. $i=2$ ); in particular, the formula (8.11) appears to be off by 2 for these two towers when $n\ge 3$ .

Example 6.7. Let C be the hyperelliptic curve over $\mathbf F_3$ given by the equation $y^2 = x^5 +x^2 + 1 $ . The function $f = x y$ has a pole of order $7$ at the unique point Q at infinity on C. We obtain a ${\mathbf Z}_3$ -tower $\mathcal {T}$ with $\mathcal {T}(0) =C$ from the Artin–Schreier–Witt equation $Fz - z = [f]$ . (Magma computes that $ \operatorname {\mathrm {Aut}}(\mathcal {T}(1)) = S_3$ , so $\mathcal {T}(1)$ cannot be a Galois ${\mathbf Z}/3^m{\mathbf Z}$ -cover of $\mathbf {P}^1$ for any $m \geq 2$ and C is the only curve for which $\mathcal {T}(1)$ is a ${\mathbf Z}/3 {\mathbf Z}$ -cover. This shows that the tower $\mathcal {T}$ is not related to a ${\mathbf Z}_p$ -tower over the projective line by adding an extra layer or modifying the base). We can compute $d_Q(\mathcal {T}(n))$ using Fact 2.2 and check that the tower is monodromy-stable. Table 29 shows some invariants of $\mathcal {T}(n)$ for small n.

Table 29 The tower $Fz - z = [xy]$ over $C: y^2 = x^5 +x^2 +1$ .

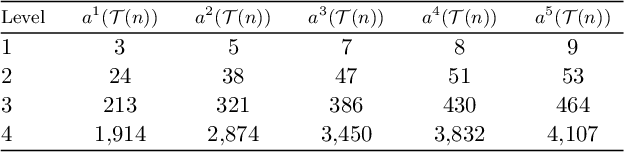
This supports Conjectures 3.7 and 3.8 and exhibits very similar behavior to basic towers with ramification invariant $7$ like the one in Example 4.2. In fact, the a-numbers look exactly the same, whereas $a^{r}(\mathcal {T}(n))$ for $r>1$ exhibits slight variation. For example, note that $7 \alpha (4,3) = 7/12$ and that for $n=3$ and $n=4$ , we have

$$\begin{align*}a^{4}(\mathcal{T}(n)) = \frac{7}{12} \left( 3^{2n} - 9 \right) + 10. \end{align*}$$

6.4 Towers with periodically stable monodromy

We next compute examples with towers $\mathcal {T}$ which are not monodromy-stable. While the behavior of $a^{r}(\mathcal {T}(n))$ in these examples does not exactly match that of monodromy-stable towers as predicted by Conjectures 3.7 and 3.8, it nevertheless appears to be quite structured, in line with Philosophy 1.1. We consider some selected towers with periodically stable monodromy, although we do not attempt to explore this situation exhaustively.

Example 6.8. Let $p=2$ and d be odd. We consider the tower

(6.3) $$ \begin{align} \mathcal{T}_d: Fy - y = [x^d] + \sum_{i=1}^{\infty} p^{2i-1} [x^{(d+2) 2^i -2}] = [x^d] + p [x^{2d+3 }] + p^3 [x^{8d+15}]+\cdots. \end{align} $$

This is ramified only over infinity. Using Fact 2.2 and Lemma 2.6, we see that $u(\mathcal {T}_d(n)) = s_n +1$ and $s(\mathcal {T}_d(n)) = s_n$ , where $s_{n+1} = (d+2) 2^n -2$ if n is even, and $s_{n+1}=(d+2) 2^n -1$ if n is odd. (Note that for n odd, the value of $u(\mathcal {T}_d(n))$ comes from the term $s_{n-1} p^{n-1-(n-2)} = p s_{n-1}$ appearing in the maximum in Fact 2.2.)

A straightforward computation with the Riemann–Hurwitz genus formula yields

$$\begin{align*}g(\mathcal{T}_d(n)) =\frac{d+2}{2}\left(\frac{2^{2n}-1}{3}\right)- \left(\frac{5}{2}+\frac{(-1)^{n-1}}{6}\right)2^{n-1} +\frac{7}{6} = \frac{d+1}{2}\left(\frac{2^{2n}-1}{3}\right)+ 2^{n-1}\left\lfloor\frac{2^n-7}{3}\right\rfloor +1, \end{align*}$$

the second expression being visibly an integer. Using Corollary 8.10, we will be able to prove that

(6.4) $$ \begin{align} a(\mathcal{T}_d(n)) = \frac{d+2}{4}\left(\frac{2^{2n-1}+1}{3}\right)+\frac{1}{4}\frac{(-2)^n-1}{3}+\frac{(-1)^{\frac{d+1}{2}}-1}{4}, \end{align} $$

valid for all n and d. Note that to fit into the framework of our previous conjectures where the a-number is a quadratic polynomial in $2^n$ , we would need the polynomial to depend on whether n is even or odd because of the presence of the $(-2)^n$ term. For monodromy-stable towers, Conjecture 3.7 predicts that the a-number is given by a single formula and does not exhibit periodic behavior. However, as the monodromy in this tower has period 2, it is not surprising that the formula (6.4) for the a-number depends on the parity of n; indeed, this is already the case for the genus.

Based on these formulae, and following the lead of Conjecture 3.4, we are led to guess the asymptotic formula

$$\begin{align*}\lim_{n\rightarrow \infty} \frac{a^{r}(\mathcal{T}_d(n))}{\alpha(r,2)(d+2)2^{2n}} = \lim_{n\rightarrow \infty} \frac{a^{r}(\mathcal{T}_d(n))}{\frac{r}{(r+3)}\left(\frac{d+2}{6}\right)2^{2n}} = 1 \end{align*}$$

with $\alpha (r,p)$ from Notation 3.3. This visibly holds for $r=1$ . For $2\le r \le 8$ , odd d with $3\le d \le 35$ , and all $2 < n\le 7$ , we computed that

(6.5) $$ \begin{align} \left|\frac{a^{r}(\mathcal{T}_d(n))}{\frac{r}{(r+3)}\left(\frac{d+2}{6}\right)2^{2n}} - 1\right| < 2^{-n}. \end{align} $$

This is consistent with the existence of a secondary term of the form $c(n)\cdot 2^n$ for some periodic function $c:{\mathbf Z}/m{\mathbf Z}\rightarrow {\mathbf Q}$ .

In light of the above, it is tempting to believe that Conjecture 3.8 may hold for arbitrary monodromy periodic towers. Direct evidence for this is somewhat elusive due to the presence of the secondary term of order $2^n$ and the fact that our computations are limited to small values of n and p. Furthermore, we have only computed with the single tower $\mathcal {T}_d$ for each value of d rather than looking at multiple towers with the same limiting ramification breaks. The behavior is clearest for $r=5$ , where our computations support the exact formula

$$\begin{align*}a^{5}(\mathcal{T}_d(n)) = \frac{d+2}{4}\left(\frac{5\cdot2^{2n-2}+1}{3}\right)+\frac{1}{4}\frac{(-2)^{n-1}-1}{3}+\frac{(-1)^{\frac{d+1}{2}}-1}{4}, \end{align*}$$

valid for all odd d with $3\le d \le 35$ and all $3\le n\le 7$ , with the sole exception of $(d,n)=(3,3)$ . In fact, further computation shows that this formula holds as well for all odd d in the range $3\le d \le 161$ and all $3\le n\le 6$ , again with the sole exception $(d,n)=(3,3)$ .

Unfortunately, we were unable to find similar exact formulae for other values of r that are uniform in d and n for n sufficiently large. Nonetheless, our limited computations support that something like Conjecture 3.8 should hold for any monodromy periodic tower, although the periodic “coefficient” functions occurring therein would appear to have a rather complicated and subtle dependence on $d_Q$ and the function $c_Q(n)$ giving the (periodic) upper ramification breaks as in Definition 2.9.

6.5 Towers with faster genus growth

Next, we collect data and make observations on a few towers with much faster genus growth. In order to be in a situation where we can have some hope of identifying patterns, we limit ourselves to cases where the genus growth is sufficiently regular. The rapid growth of the genus in these examples limits our computations to characteristic $p=2$ and levels $n\le 6$ .

Example 6.9. Let d be a positive odd integer. In characteristic $p=2$ , we consider the towers

$$ \begin{align*} \mathcal{T}_d : Fy - y = \sum_{n\ge 0} 2^n [x^{s_n}] \end{align*} $$

with $s_n:=(d+2)\cdot 2^{2n+1}-1$ . Note that $s_{\infty }(\mathcal {T}_d(n)) = s_{n-1}$ for $n\ge 1$ . Using the Riemann–Hurwitz formula in the form of Lemma 2.7, we have

$$ \begin{align*} g(\mathcal{T}_d(n)) = \frac{(d+2)}{7}(2^{3n}-1)-2^n+1. \end{align*} $$

We computed $a^{r}(\mathcal {T}_d(n))$ for $r\le 10$ and $n\le 6$ , with $d\in \{1,3,5,7,9\}$ . Inspired by Conjecture 3.4 and Corollary 3.5, we first analyzed the ratio

(6.6) $$ \begin{align} \frac{a^{r}(\mathcal{T}_d(n))}{\frac{(d+2)}{7}\cdot 2^{3n}} \end{align} $$

for each value of r and d, and all $n\le 6$ . For each fixed r, this ratio appears to stabilize as n increases, to a value that appears not to depend on d. Working in level $n=6$ and truncating the resulting limiting values to six decimal places, we then used continued fraction expansions to find best possible rational approximations with comparatively small denominator, which leads to the following guesses for the main term of $a^{r}(\mathcal {T}_d(n))$ .

Definition 6.10. For $r\le 10$ , define

$$ \begin{align*} \nu_{d,r}(n):=\left\lfloor\frac{d+2}{7} \alpha(r) 2^{3n}\right\rfloor, \end{align*} $$

where $\alpha (r)$ is given in Table 30.

Table 30 Leading constants for $\mathcal {T}_d$ .

Thanks to Corollary 8.10, we have the exact formula

$$\begin{align*}a(\mathcal{T}_d(n)) = \frac{3}{8} \cdot \frac{d+2}{7}\cdot 2^{3n} + \frac{d-5}{14} = \frac{d+2}{2}\left(\frac{3\cdot 2^{3n -2}+1}{7}\right)-\frac{1}{2} \end{align*}$$

for all n and d, which provides a proof that the ratio (6.6) tends to $3/8$ as $n\rightarrow \infty $ . In a similar spirit, we compute that

(6.7) $$ \begin{align} a^{2}(\mathcal{T}_d(n+1)) - 8 a^{2}(\mathcal{T}_d(n)) = 3 \frac{5-d}{2}+7\left\lfloor\frac{d-1}{8}\right\rfloor \end{align} $$

for all $d \in \{1,3,5,7,9\}$ and $2 \leq n \leq 5$ , and

(6.8) $$ \begin{align} a^{3}(\mathcal{T}_d(n+1)) - 8 a^{3}(\mathcal{T}_d(n)) =\begin{cases} 7, & 3 \leq n \leq 5, \\ 3, & n=2,\end{cases} \end{align} $$

for all $d \in \{1,3,5,7,9\}$ . These lead to the conjectural exact formulae

$$\begin{align*}a^{2}(\mathcal{T}_d(n)) = \frac{37}{64}\cdot \frac{d+2}{7} \cdot 2^{3n} +3\frac{d-5}{14} -\left\lfloor\frac{d-1}{8}\right\rfloor= \frac{d+2}{8}\left(\frac{37\cdot 2^{3(n -1)}+5}{7}\right)-1 +\frac{d\bmod 8 - 2}{8} \end{align*}$$

for $n\ge 2$ (where $d\bmod 8$ denotes the least nonnegative residue of d modulo $8$ ) and

$$\begin{align*}a^{3}(\mathcal{T}_d(n)) = \frac{91}{128}\cdot \frac{d+2}{7} \cdot 2^{3n} -1 = 13(d+2)2^{3n-7} - 1 \end{align*}$$

for $n\ge 3$ . These conjectural formulae support the given values of $\alpha (r)$ for $r=2,3$ ; note that these values of $\alpha $ arise naturally from (6.7) and (6.8) and the computed values of $a^r(\mathcal {T}_d(n))$ for $n=2$ . Thus, it is perhaps unsurprising that the values of $\alpha $ do not appear to satisfy a simple formula.

Remark 6.11. The special formulae

$$ \begin{align*} a^{2}(\mathcal{T}_d(1)) = \frac{3d+(-1)^{(d-1)/2}}{4}+1 \quad \text{and} \quad a^{3}(\mathcal{T}_d(2)) = 6(d+2)+\frac{d+1}{2} \end{align*} $$

hold for all (positive, odd) values of d less than $30$ in levels 1 and 2, respectively. However, we could not discern any pattern for the values of $a^{3}(\mathcal {T}_d(1))$ in level 1.

For $r> 3$ , the differences $a^{r}(\mathcal {T}_d(n+1)) - 8 a^{r}(\mathcal {T}_d(n))$ are comparatively small, but do not seem to obey any obvious pattern. Nonetheless, for all values of r, d, and n for which we computed $a^{r}(\mathcal {T}_d(n))$ , this integer is remarkably close to $\nu _{d,r}(n)$ , and we tabulate the differences $a^{r}(\mathcal {T}_d(n)) - \nu _{d,r}(n)$ for $4 \le r \le 10$ , $d\in \{1,3,5,7,9,11\}$ , and $1\le n\le 6$ in Table 31.

Table 31 $a^{r}(\mathcal {T}_d(n)) - \nu _{d,r}(n)$ .

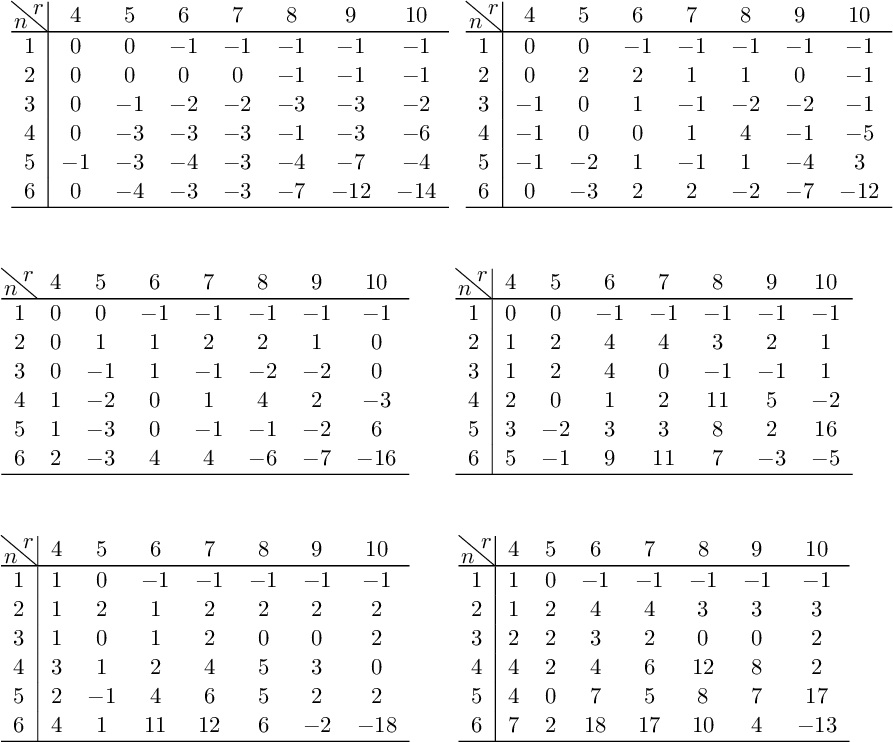
6.6 Non- ${\mathbf Z}_p$ -towers

In contrast, we now give an example of a sequence of Artin–Schreier covers in characteristic 3 which are not part of a ${\mathbf Z}_3$ -tower but have the same ramification as we would see in a basic ${\mathbf Z}_p$ -tower.

Example 6.12. Take $p=3$ and $k= \mathbf F_p$ . Let $C_0 = \mathbf {P}^1_{k}$ with function field $k(x)$ , and for $1 \leq i \leq 4$ , construct the curve $C_i$ by adjoining a root of $y_i^3 - y_i = f_i$ to $k(C_{i-1})$ , where $f_1 = x^7$ , $f_2 = x^{14} y_1$ , $f_3 = x^{42}y_2$ , and $f_4 = x^{126} y_3$ . It is straightforward to verify that $C_i \to C_{i-1}$ is totally ramified over the point above infinity, with ramification invariants $7, 49, 427, 3,829$ . This is the same sequence of layer-by-layer ramification breaks and genera as for basic ${\mathbf Z}_3$ -towers with ramification invariant $7$ , which we looked at in Example 4.2. However, these curves do not form the first four layers of a ${\mathbf Z}_3$ -tower—one can check (using Magma, or directly) that $k(C_2)$ is not normal over $k(x)$ . Similarly, define $C^{\prime }_i$ for $1\leq i \leq 4$ using $f^{\prime }_1 = x^7$ , $f^{\prime }_2 = x^{14}y_1 + x^2$ , $f^{\prime }_3 = (x^{42} + x^{20}) y_2 + x y_1$ , and $f^{\prime }_4 = x^{126} y_3 + x^5 y_2 + x^2$ , where we have added some lower-order terms to the Artin–Schreier equations for $C_i$ . Table 32 records invariants of these sequences of curves.

Table 32 Invariants of $C_n$ and $C^{\prime }_n$ for $1 \leq n \leq 4$ .

Table 33 Approximate running times to compute $a(\mathcal {T}(n))$ for the ${\mathbf Z}_3$ -tower $\mathcal {T}_{\textrm {time}} : Fy -y = [x^7] + [x^5]$ .

They are much less structured that what we have seen for ${\mathbf Z}_p$ -towers. For example, based on the first three curves, it would be reasonable to guess that

$$\begin{align*}a(C_n) = a(C^{\prime}_n) = \frac{5}{16} 3^{2n} + \frac{1}{12} 3^n + \frac{15}{16} \end{align*}$$

as this holds for $n =1,2,3$ and the proposed formula has relatively small denominators. This would predict that the a-number of $C_4$ and $C^{\prime }_4$ would be $2,058$ . While $a(C_4)$ is close, $a(C^{\prime }_4)$ is considerably different. Higher powers of the Cartier operator display similar irregularity. Furthermore, $\frac {a(C_4)}{g(C_4)}$ and $\frac {a(C^{\prime }_4)}{g(C_4)}$ are around $.361$ and $.355$ , respectively, whereas this ratio is much closer to $\frac {1}{3}$ for basic ${\mathbf Z}_3$ -towers having similar ramification. This suggests that it is crucial that a sequence of Artin–Schreier covers actually form a ${\mathbf Z}_p$ -tower in order to obtain exact (or even just asymptotic) formulae for $a^{r}(C_n)$ when $n\gg 0$ .

It is also curious that this ratio is not particularly close to $\frac {1}{2}(1-p^{-1})(1-p^{-2}) = 8/27 \approx 0.296$ , the naïve guess articulated below equation (1.5). Possibly that guess is wrong. On the other hand, these are examples in which $n=4$ and it would be reasonable to expect noise on the order of $3^{-4} \approx 0.0123$ . Furthermore, we chose the ${\mathbf Z}/3{\mathbf Z}$ -covers, so they could be described by Artin–Schreier equations with relatively few terms, which is not the generic behavior of random covers.

7 Computing with the Cartier operator in towers

Let k be a finite field of characteristic p, and let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower over k. Suppose that the base of the tower is the projective line (i.e., $\mathcal {T}(0) = \mathbf {P}^1_k$ ) and that $\mathcal {T}$ is totally ramified over infinity and unramified elsewhere. In this section, we describe how to compute efficiently with the Cartier operator on the space of regular differentials on $\mathcal {T}(n)$ . The key difficulty is that $g(\mathcal {T}(n))$ grows at least exponentially in n (see Remark 2.8), so the dimension of the space of regular differentials on $\mathcal {T}(n)$ quickly becomes intractably large as n increases. In order to compute with enough levels of $\mathcal {T}$ to have any hope of systematically investigating Philosophy 1.1, we must be as efficient as possible.

The Magma computer algebra system has extensive, robust algorithms for function fields; in particular, it has the ability to compute with Witt vectors and Artin–Schreier–Witt extensions in characteristic p, and to compute a matrix representation of the Cartier operator on the space of regular differentials on the smooth projective curve associated with any function field over k. Unfortunately, these algorithms are not efficient enough to compute beyond the first few levels in a ${\mathbf Z}_p$ -tower, which severely limits the computational support they can provide for our conjectures. For example, Table 33 shows the time needed to compute the a-number of the first few levels of the basic ${\mathbf Z}_3$ -tower $\mathcal {T}_{\textrm {time}} : Fy - y = [x^7] + [x^5]$ in characteristic $3$ using Magma’s default methods and using our more efficient methods. ¹⁴ (These computations also use substantial amounts of memory. For example, our method used several gigabytes of memory for the fifth level.)

We have implemented our algorithm in Magma [BC2] in order to build on Magma’s support of efficient computations with polynomials and efficient linear algebra over finite fields. The key improvement is incorporating theoretic information about the space of regular differentials in a ${\mathbf Z}_p$ -tower. An overview of our algorithm is as follows.

1. 1. Perform computations with Witt vectors to turn a description of a ${\mathbf Z}_p$ -tower using Artin–Schreier–Witt theory into a description of the tower as a sequence of ${\mathbf Z}/p{\mathbf Z}$ -covers. This uses techniques and functions developed by Finotti for performing computations with Witt vectors [F1], [F2] which are substantially faster than the native Witt vector algorithms of Magma.

2. 2. Rewrite the sequence of Artin–Schreier ${\mathbf Z}/p{\mathbf Z}$ -covers describing the tower in a standard form (discussed in §7.2).

3. 3. Using results of [M1] for ${\mathbf Z}/p^n{\mathbf Z}$ -covers of $\mathbf {P}^1_k$ in the above standard form, write down an explicit basis of regular differentials on $\mathcal {T}(n)$ (see §7.3).

4. 4. Recursively compute the images under the Cartier operator of a subset of this basis which suffices to compute the image of any differential using semilinearity.

5. 5. Build a matrix representing the Cartier operator and compute the kernel of its rth power to obtain $a^{r}(\mathcal {T}(n))$ .

In the remainder of this section, we explain these steps in detail.

Remark 7.1. We will not present a careful asymptotic analysis of the running time of the algorithm because it is still exponential in n like Magma’s default functionality. Roughly speaking, the algorithm is polynomial time in the genus of $\mathcal {T}(n)$ ; this is very bad as $g(\mathcal {T}(n))$ grows exponentially in n. Therefore, this can only be practical for small n. (For a basic ${\mathbf Z}_p$ -tower with ramification invariant d, Lemma 2.13 says that $g(\mathcal {T}(n)) = \Theta (d p^{2n})$ ). The advantage of our algorithm over the default methods available in Magma is that it is much faster in practice, allowing us to compute further with basic towers and provide much stronger evidence for our conjectures.

Remark 7.2. For $p>2$ , the bottleneck in our algorithm is usually the computations with the Cartier operator in step 4. Writing down the tower in standard form and carrying out the linear algebra are substantially faster than carrying out the computations with the Cartier operator for the fifth level.

When $p=2$ , other parts of the computation are the bottleneck. For example, we are able to compute with the seventh level of many ${\mathbf Z}_2$ -towers (and sometimes the eighth level for very simple towers like the one in Example 5.7). In these examples, writing a basic ${\mathbf Z}_2$ -tower in standard form (step 2) is often the bottleneck, or occasionally the computations with Witt vectors (step 1). For towers with faster growth like in §6.5 in characteristic 2, the linear algebra computations (step 5) are actually the bottleneck.

Remark 7.3. When Magma does a similar computation, most of the time is spent finding a basis of the regular differentials on $\mathcal {T}(n)$ . After Magma has pre-computed a basis for the regular differentials on $\mathcal {T}(n)$ (e.g., in the course of computing the genus), Magma can produce a matrix representing the Cartier operator and compute $a^{r}(\mathcal {T}(n))$ quickly relative to the time spent finding the basis.

Remark 7.4. Our program assumes that the base of the ${\mathbf Z}_p$ -tower is the projective line and that the tower is totally ramified over infinity and unramified elsewhere. The first assumption is essential to present the tower in standard form and use the results of [M1] to write down a basis of regular differentials. If the tower has a different base, it may not be possible to write it in standard form (see §7.2).

The second assumption, that there is only one point of ramification, is not essential, but makes many of the computations simpler. In particular, it allows representing differentials as polynomials instead of rational functions. As the bulk of computation time is spent performing computations with these polynomials, this is an important simplification.

7.1 Computations with Witt vectors

The polynomials defining addition (and multiplication) for the length-n Witt vectors become increasingly complicated as n increases. Such computations are necessary to convert the Artin–Schreier–Witt description of a ${\mathbf Z}_p$ -tower as in §2 into explicit Artin–Schreier equations for each layer of the tower as a ${\mathbf Z}/p{\mathbf Z}$ -cover of the previous layer. Magma has the functionality to compute with Witt vectors, but we use the methods of Finotti [F1], [F2], which are more efficient. The calculations with Witt vectors are rarely the limiting factor in our computations—for example, these computations (using either method) for the fourth level of the ${\mathbf Z}_3$ -tower $\mathcal {T}_{\textrm {time}}$ appearing in Table 33 take well under a second, whereas the overall computation is substantially longer. It is only for a ${\mathbf Z}_2$ -tower like $\mathcal {T}' : Fy - y = [x^3]$ in characteristic 2 where the ramification invariant is very small and the Artin–Schreier–Witt equation is very simple that the computations with Witt vectors take substantial time compared with the other parts of the computation. In particular, the Witt vector computations needed to analyze the eighth level of $\mathcal {T}'$ using Finotti’s algorithms took about 6 hours (and then around 40 more minutes to compute the a-number), whereas Magma’s native functionality did not finish the Witt vector computations within $24$ hours.

7.2 Standard form for Artin–Schreier–Witt towers

Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower over a finite field k of characteristic p ramified over $S \subset \mathcal {T}(0)$ . For $Q \in S$ , let $Q(n)$ be the unique point of $\mathcal {T}(n)$ over Q. The function field of $\mathcal {T}(n)$ is an Artin–Schreier extension of $\mathcal {T}(n-1)$ , given by adjoining a root of the Artin–Schreier equation

$$\begin{align*}y_n^p - y_n = f_n \end{align*}$$

for some $f_n \in k(\mathcal {T}(n-1))$ . This representation is of course not unique: making the change of variable $y_n' = y_n + z$ replaces $f_n$ by $f_n' = f_n + z^p - z$ but gives an isomorphic extension of fields.

Definition 7.5. We say that the functions $(f_1,f_2,\ldots )$ present the tower $\mathcal {T}$ in standard form provided that for all positive integers n, we have $d_Q(\mathcal {T}(n)) = \operatorname {\mathrm {ord}}_{Q(n-1)}(f_n)$ for all $Q \in S$ and $f_n$ is regular away from the points of $\mathcal {T}(n-1)$ over S. We can analogously talk about a single ${\mathbf Z}/p{\mathbf Z}$ -cover being presented in standard form.

Remark 7.6. Over the projective line, the theory of partial fractions allows one to write every ${\mathbf Z}/p{\mathbf Z}$ -cover of the projective line in standard form.

If $d_Q(\mathcal {T}(n)) \neq \operatorname {\mathrm {ord}}_{Q(n-1)}(f_n)$ , it is always possible to locally modify the presentation of $\mathcal {T}(n) \to \mathcal {T}(n-1)$ so that $d_Q(\mathcal {T}(n)) = \operatorname {\mathrm {ord}}_{Q_n}(f^{\prime }_n)$ by making a change of variable $y_n' = y_n + z$ where z has the appropriate local behavior at $Q(n-1)$ . However, it is not always possible to do so at each ramified point while keeping $f^{\prime }_n$ regular away from the points of $\mathcal {T}(n-1)$ above S (see [S2, §7], especially the second example after Proposition 49). Therefore, the following result of Madden about towers over the projective line is initially surprising.

Fact 7.7 [M1, Th. 2].

Every ${\mathbf Z}_p$ -tower over the projective line can be presented in standard form.

While it is essential for our computations that we work with a tower in standard form, the description of the tower as a sequence of Artin–Schreier extensions produced by Artin–Schreier–Witt theory need not be in standard form. Thus, a key step in our computations is to explicitly rewrite the given Artin–Schreier–Witt description of a tower in standard form.

Let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower with base the projective line (with function field $k(x)$ ) that is totally ramified over infinity and unramified elsewhere. Let $P(n)$ be the unique point of $\mathcal {T}(n)$ above infinity. Suppose that the first $n-1$ levels of the tower are written in standard form using Artin–Schreier equations $y_i^p - y_i = f_i$ . We will describe how to rewrite the nth level in standard form.

Let the nth level be given by an Artin–Schreier equation

$$\begin{align*}y_n^p - y_n = f, \end{align*}$$

where f is a polynomial in x and $y_1,\ldots , y_{n-1}$ . Note that $\operatorname {\mathrm {ord}}_{P(i)}(y_i) = \operatorname {\mathrm {ord}}_{P(i-1)}(f_i) = d_{\infty }(\mathcal {T}(i))$ for $i < n$ . The nth level is not in standard form precisely if $\operatorname {\mathrm {ord}}_{P(n-1)}(f)$ is a multiple of p, which necessarily must be larger than $d(\mathcal {T}(n))$ [S4, Prop. 3.7.8]. We may effectively write it in standard form if we can always produce a function z on $\mathcal {T}(n-1)$ with a pole of order $\operatorname {\mathrm {ord}}_{P(n-1)}(f)/p $ at $P_{n-1}$ that is regular elsewhere: changing variables by an appropriate multiple of z, which replaces f by $f + (cz)^p - cz$ , will cancel out the leading term, after which we repeat this process. The proof of [M1, Th. 2] shows that there exists nonnegative integers $\nu $ and $a_1,\ldots , a_{n-1}$ such that $z= x^{\nu } y_1^{a_1}, \ldots , y_{n-1}^{a_{n-1}}$ has the desired valuation (see in particular [M1, Lem. 3] and the subsequent decomposition of $L(\mathfrak {a}^{-1})$ ).

Remark 7.8. While conceptually easy, this is still computationally nontrivial as f can have an enormous number of terms and require many iterations of the above procedure before ending up in standard form. For example, putting the first five levels of the ${\mathbf Z}_3$ -tower $\mathcal {T}_{\textrm {time}}: Fy - y = [x^7] + [x^5]$ in standard form took a bit over 3 minutes.

7.3 A basis for regular differentials

As before, let $\mathcal {T}$ be a ${\mathbf Z}_p$ -tower over a finite field k of characteristic p whose base is the projective line, totally ramified over infinity and unramified elsewhere. We identify $k(x)$ with the function field of $\mathcal {T}(0)$ , and present the tower in standard form as a sequence of Artin–Schreier extensions given by $y_n^p-y_n = f_n$ . Using the presentation of the tower in standard form, Madden’s work [M1] gives us an explicit basis for the space of regular differentials on $\mathcal {T}(n)$ .

Definition 7.9. Let $ \mathscr {S}_n$ be the set of $n+1$ tuples of integers $(\nu ,a_1,\ldots ,a_n)$ such that:

1. 1. $0 \leq a_i <p$ for all i;

2. 2. $\displaystyle 0 \leq p^n \nu \leq \left (\sum _{j=1}^n p^{n-j} d_{\infty }(\mathcal {T}(j)) (p-1-a_j) \right ) - p^n -1$ .

For $s = (\nu ,a_1,\ldots ,a_n) \in \mathscr {S}_n$ , define the differential

As $\mathcal {T}$ is presented in standard form, [M1, Lem. 5] gives the following result.

Fact 7.10. The set $\{\omega _s : s \in \mathscr {S}_n \}$ is a basis for $H^0(\mathcal {T}(n),\Omega ^1_{\mathcal {T}(n)})$ .

7.4 A matrix for the Cartier operator

We continue with the notation of §7.3. To represent the Cartier operator on $H^0(\mathcal {T}(n),\Omega ^1_{\mathcal {T}(n)})$ as a matrix, it suffices to compute $V_{\mathcal {T}(n)}(\omega _s)$ for $s \in \mathscr {S}_n$ . As the Cartier operator is $p^{-1}$ -semilinear, we have

$$ \begin{align*} V_{\mathcal{T}(n)} \left( x^{\nu} y_1^{a_1} \ldots y_n^{a_n} dx \right) & = V_{\mathcal{T}(n)} \left( x^{\nu} y_1^{a_1} \ldots y_{n-1}^{a_{n-1}} (y_n^p - f_n)^{a_n} dx \right) \\ &= \sum_{i=0}^{a_n} \binom{a_n}{i} y_n^i V_{\mathcal{T}(n)} \left( x^{\nu} y_1^{a_1} \ldots y_{n-1}^{a_{n-1}} (- f_n)^{a_n-i} dx \right)\!. \end{align*} $$

Notice that $x^{\nu } y_1^{a_1} \ldots y_{n-1}^{a_{n-1}} (- f_n)^{a_n-i} dx$ does not depend on $y_n$ , and is a rational differential one-form on $\mathcal {T}(n-1)$ . Thus, we may compute $V_{\mathcal {T}(n)}(\omega _s)$ by applying the Cartier operator to (several) differentials on $\mathcal {T}(n-1)$ . This gives a recursive method to compute with $V_{\mathcal {T}(n)}$ , ultimately reducing to computing with the Cartier operator on the base curve, the projective line.

This is the most computationally expensive step of the algorithm. The genus $g(\mathcal {T}(n))$ grows (at least) exponentially with n, and we must evaluate the Cartier operator on $g(\mathcal {T}(n))$ differentials. Furthermore, the function $f_n$ can have an enormous number of terms; its order at the point above infinity is $-d_{\infty }(\mathcal {T}(n))$ , which is also growing (at least) exponentially in n.

Remark 7.11. The basic tower $Fy - y = [x^d]$ is always substantially faster to compute with precisely because the polynomials $f_n$ presenting the tower in standard form are (somewhat) simpler. For example, building a matrix representing the Cartier operator on the fifth level of the ${\mathbf Z}_3$ -tower given by $Fy - y = [x^4]$ takes less than 15 minutes, whereas doing the same for $Fy -y = [x^4] + [x^2]$ takes more than 3.5 hours.

To implement the step described above, we first pre-compute

(7.1) $$ \begin{align} V_{\mathcal{T}(m)} \left( x^{\nu} y_1^{a_1} \ldots y_m^{a_m} dx \right) \end{align} $$

with $0 \leq \nu <p$ and $0\leq a_i <p$ for $1 \leq i \leq m$ for $m=1,2,\ldots ,n$ . The computation at level m makes use of the pre-computations at level $m-1$ . Note that the semilinearity of the Cartier operator allows us to compute $V_{\mathcal {T}(m)}(\omega _s)$ as a $k(x)$ -linear combination of these special values quickly.

Remark 7.12. To give some context, for the basic ${\mathbf Z}_3$ -tower $\mathcal {T}_{\textrm {time}}: Fy - y = [x^7]+[x^5]$ , the pre-computations up to level $5$ took about 6 hours. Once they are completed, it takes less than 4 minutes to use them to build a matrix for the Cartier operator on the fifth level of the tower. As $g(\mathcal {T}_{\textrm {time}}(5)) = 51,546$ , this matrix has more than $2.6$ billion entries!

Remark 7.13. As all of the $p^{m+1}$ pre-computations of (7.1) with $ 0\leq \nu <p$ and $0 \leq a_i <p$ for level m can be performed independently using the results from level $m-1$ , this step would be amenable to parallelization.

7.5 Linear algebra over finite fields

Linear algebra over small finite fields is very efficient in Magma. For a basic ${\mathbf Z}_3$ -tower like $\mathcal {T}_{\textrm {time}}: Fy - y = [x^7]+[x^5]$ , whose fifth level has genus $51,546$ , computing the dimension of the kernel of the $51,546$ by $51,546$ matrix representing the Cartier operator on the space of regular differentials takes about 1.5 minutes. Some of the matrices we consider, such as those in §6.5, are of course even larger, and consume many gigabytes of memory in storage.

8 Theoretical evidence

In this section, we study the interaction of the trace map on differential forms with the Cartier operator in Artin–Schreier extensions. We use this to provide theoretical evidence for our conjectures about the a-number in characteristic 2, in particular proving Conjecture 4.1 for basic ${\mathbf Z}_2$ -towers and more generally proving Conjecture 3.7 for ${\mathbf Z}_2$ -towers.

The following fact is standard and will be used repeatedly (see, e.g., [BC1, Lem. 3.7]).

Fact 8.1. Let $\pi : Y \to X$ be a ${\mathbf Z}/p{\mathbf Z}$ -cover of curves over a perfect field k of characteristic p, with Artin–Schreier equation $y^p - y = \psi $ . If the defining equation is in standard form at a branch point Q with ramification invariant $d_Q$ (i.e., $\operatorname {\mathrm {ord}}_Q(\psi ) = -d_Q$ ), then a meromorphic differential $\displaystyle \omega = \sum _{i=0}^{p-1} \omega _i y^i$ on Y is regular above Q if and only if

$$ \begin{align*} \operatorname{\mathrm{ord}}_Q(\omega_i) \geq - \left \lceil \frac{(p-1-i) d_Q}{p} \right \rceil \quad \text{ for } 0 \leq i \leq p-1. \end{align*} $$

8.1 Vanishing trace

Let $\pi :Y\rightarrow X$ be a ${\mathbf Z}/p{\mathbf Z}$ -cover with branch locus S, and for $Q \in S$ , let $d_Q$ be the ramification invariant above Q.

Associated with the finite map $\pi $ is a canonical $\mathscr {O}_X$ -linear trace morphism $\pi _* \Omega ^1_{Y/k}\rightarrow \Omega ^1_{X/k}$ which is dual, via Grothendieck–Serre duality, to the usual pullback morphism $\mathscr {O}_X\rightarrow \pi _*\mathscr {O}_Y$ on functions. We will write $\pi _*$ for the induced trace map on global differential forms. Note that the Cartier operator is induced by the trace morphism $F_*$ attached to absolute Frobenius; since Frobenius commutes with arbitrary ring maps, it in particular commutes with $\pi $ and it follows that the trace map commutes with the Cartier operator. We will use the following formula repeatedly

(8.1) $$ \begin{align} \pi^* \pi_* = \sum_{g\in {\mathbf Z}/p{\mathbf Z}} g^*. \end{align} $$

In characteristic 2, we can be very explicit about the kernel of the trace map.

Lemma 8.2. If $p=2$ , the kernel of $\pi _*$ on $H^0(Y,\Omega ^1_{Y})$ is isomorphic to $H^0(X,\Omega ^1_X(\sum _{Q \in S} \lceil d/2 \rceil [Q]))$ .

Proof. For $Q \in S$ , locally express the cover as an Artin–Schreier extension $y^2 - y = f$ in standard form at Q with $g^*y=y+1$ for the nontrivial element $g\in {\mathbf Z}/2{\mathbf Z}$ . A general meromorphic differential on Y may be written as $\eta =\omega _0 + y \omega _1$ with $\omega _0, \omega _1$ meromorphic differentials on X. By (8.1), $\pi _*\eta =0$ forces $\omega _1=0$ , and $\eta $ is regular at Q if and only if $\operatorname {\mathrm {ord}}_Q(\omega _0) \geq - \lceil d/2 \rceil $ (see Fact 8.1).

We next analyze the trace of differentials killed by the Cartier operator.

Theorem 8.3. If $\eta \in H^0(Y,\Omega ^1_Y)$ is killed by $V_Y$ , then for every branch point $Q \in S$ , we have $\operatorname {\mathrm {ord}}_Q(\pi _*(\eta )) \ge d_Q -\lceil d_Q/p \rceil $ with strict inequality when $d_Q \equiv \lfloor d_Q/p \rfloor \bmod p$ .

Proof. We may work locally at Q, where the extension is given by an Artin–Schreier equation $y^p-y = \psi $ with . We write $d=pq+r$ with $0 < r < p$ , and decompose

$$\begin{align*}\eta = \sum_{i=0}^{p-1} \omega_i y^i \end{align*}$$

with the $\omega _i$ differentials on X. If $\eta $ is regular above Q, Fact 8.1 implies that $\operatorname {\mathrm {ord}}_Q(\omega _i) \ge - \lceil (p-1-i)d/p\rceil $ . Furthermore, substituting $y=y^p-\psi $ in the expression for $\eta $ above, and using the fact that V is additive and $p^{-1}$ -linear, we compute (as in [BC1, Lem. 4.1]) that

$$\begin{align*}V_Y(\eta) = \sum_{i=0}^{p-1} \left( \sum_{j=i}^{p-1} \binom{j}{i} V_X(\omega_j(-\psi)^{j-i})\right) y^i. \end{align*}$$

The assumption that $V_Y(\eta )=0$ implies that $V_X(\omega _{p-1})=0$ and that for $0\le i\le p-2$ ,

(8.2) $$ \begin{align} V_X(\omega_{p-1}(-\psi)^{p-1-i}) = - \sum_{j=i}^{p-2}\binom{j}{i} V_X(\omega_j(-\psi)^{j-i}). \end{align} $$

It is straightforward to check that the order of vanishing of the right side of (8.2) at Q is at least $\operatorname {\mathrm {ord}}_Q(V_X(\omega _{p-2}(-\psi )^{p-2-i}))$ , from which we deduce (replacing i with $p-1-i$ ) that

(8.3) $$ \begin{align} \operatorname{\mathrm{ord}}_Q(V_X(\omega_{p-1}(-\psi)^i)) \ge - \left\lceil\frac{(i-1)d + \lceil d/p \rceil}{p} \right\rceil = -(i-1)q - \left\lceil \frac{(i-1)r + q +1}{p} \right\rceil\! . \end{align} $$

Let u be a uniformizer at Q. We may write $-\psi = cu^{-d}v$ with $c\in k^{\times }$ and v a one-unit in the local ring at Q. Working in the complete local ring at Q, as $p\nmid d$ Hensel’s lemma implies, there exists a one-unit w with $w^{-d}=v$ , whence $-\psi = cu^{-d}w^{-d} = c z^{-d}$ with a uniformizer at Q. Let $r_i$ be the least nonnegative residue of $ir$ modulo p, so that $id = i(pq+r) = p(iq + \lfloor ri/p \rfloor ) + r_i$ ; then

$$\begin{align*}V_X(\omega_{p-1}(-\psi)^i) = V_X(\omega_{p-1}c^iz^{-di}) = c^{i/p}z^{-iq-\lfloor ri/p \rfloor} V_X(\omega_{p-1}z^{-r_i}). \end{align*}$$

We obtain

(8.4) $$ \begin{align} \operatorname{\mathrm{ord}}_Q(V_X(\omega_{p-1}(-\psi)^i)) = -iq - \lfloor ri/p \rfloor + \operatorname{\mathrm{ord}}_Q(V_X(\omega_{p-1}z^{-r_i})). \end{align} $$

Combining this with (8.3) gives

$$\begin{align*}\operatorname{\mathrm{ord}}_Q(V(\omega_{p-1}z^{-r_i})) \ge q +\left\lfloor \frac{ri}{p} \right\rfloor- \left\lceil \frac{(i-1)r + q +1}{p} \right\rceil\!. \end{align*}$$

As z is a uniformizer, the set $\{z^i\}_{0\le i< p}$ is a p-basis for $\widehat {\mathscr {O}}_{X,Q}\simeq k[\![z]\!]$ , so we may write

(8.5) $$ \begin{align} \omega_{p-1} = (f_1^p z + f_2^p z^2 + \cdots + f_{p-1}^p z^{p-1} + f_p^p z^p) \frac{dz}{z}, \end{align} $$

where $f_i$ are local functions. Since $V_X(\omega _{p-1})=0$ , we have $f_p=0$ , and we compute

$$\begin{align*}V(\omega_{p-1} z^{-r_i}) = f_{r_i} \frac{dz}{z}. \end{align*}$$

Therefore, we conclude that for $1\le i \le p-1$ ,

(8.6) $$ \begin{align} \operatorname{\mathrm{ord}}_Q(f_{r_i}) - 1 \ge q +\left\lfloor \frac{ri}{p} \right\rfloor- \left\lceil \frac{(i-1)r + q +1}{p} \right\rceil\!. \end{align} $$

Let $s_i$ be the least nonnegative residue of $(i-1)r + q + 1$ modulo p, so that

$$\begin{align*}p \left\lceil \frac{(i-1)r + q +1}{p} \right\rceil = (i-1)r+q+1 - s_i + \begin{cases} p, & s_i\neq 0, \\ 0, & s_i =0.\end{cases} \end{align*}$$

We find

$$ \begin{align*} \operatorname{\mathrm{ord}}_Q(f_{r_i}^p z^{r_i} \frac{dz}{z}) &\ge pq +p\left(\left\lfloor \frac{ri}{p} \right\rfloor- \left\lceil \frac{(i-1)r + q+1}{p} \right\rceil+1\right)+ ri - p\left\lfloor\frac{ri}{p}\right\rfloor - 1 \\ & = pq + ri +p - 1 - p\left\lceil \frac{(i-1)r + q+1}{p} \right\rceil \\ & = pq + ri +p - 1 - (i-1)r - (q+1) + s_i - \begin{cases} p, & s_i\neq 0 \\ 0, & s_i =0\end{cases}\\ &= (pq+r) - (q+1) + p-1+s_i -\begin{cases} p, & s_i\neq 0 \\ 0, & s_i =0\end{cases} \\ &= d - \lceil d/p \rceil + \begin{cases} s_i - 1, & s_i\neq 0, \\ p-1, & s_i =0.\end{cases} \end{align*} $$

If $q\not \equiv r \bmod p$ , we claim that there exists i with $1\le i \le p-1$ and $s_i = 1$ . Indeed, $i = (1 - q r^{-1} \bmod p)$ does the trick. On the other hand, if $q\equiv r\bmod p$ , then $(i-1)r + q \equiv i r \bmod p$ , which is never $0 \bmod p$ , so that $s_i\neq 1$ for all i with $1\le i \le p-1$ in this case. We conclude that

$$\begin{align*}\operatorname{\mathrm{ord}}_Q(\omega_{p-1}) \ge d - \left\lceil \frac{d}{p} \right \rceil, \end{align*}$$

and that the inequality is strict if $q\equiv r \bmod p$ , or what is the same, if $\lfloor d/p \rfloor \equiv d\bmod p$ .

Corollary 8.4. Suppose that $\displaystyle \sum _{Q\in S} (d_Q -\lceil d_Q/p\rceil ) \ge 2g(X)-2$ , with strict inequality when $d_Q\not \equiv \lfloor d_Q/p\rfloor \bmod p$ for all $Q \in S$ . If $\eta \in H^0(Y,\Omega ^1_Y)$ is killed by $V_Y$ , then $\pi _*(\eta )=0$ .

Proof. As the differential $\pi _*(\eta )$ is regular when $\eta $ is, the corollary follows immediately from the fact that for an effective divisor D, one has $H^0(X,\Omega ^1_X(-D))=0$ whenever $\deg (D)> 2g-2$ .

Finally, for a ${\mathbf Z}_p$ -tower $\mathcal {T}$ totally ramified over a nonempty set S, we investigate the hypothesis

(8.7) $$ \begin{align} \sum_{Q\in S} (d_Q(\mathcal{T}(n+1)) -\lceil d_Q(\mathcal{T}(n+1))/p\rceil)> 2g(\mathcal{T}(n))-2. \end{align} $$

For convenience, we define

Lemma 8.5. Suppose that there exists an integer N such that

(8.8) $$ \begin{align} \sum_{Q \in S} (s_Q(\mathcal{T}(j+1)) - 2s_Q(\mathcal{T}(j)) \ge 2 g(\mathcal{T}(0))-2 + \# S\quad\text{for all}\ j>N. \end{align} $$

If (8.8) is an equality for all $j>N$ , assume moreover that $\Delta _N> 0$ . Then $\mathcal {T}$ satisfies (8.7) for $n \gg 0$ .

Proof. As we only deal with one tower in this proof and its corollary, to simplify notation, we will let $d_{Q,n}$ (resp. $s_{Q,n}$ , $g_n$ ) denote $d_Q(\mathcal {T}(n))$ (resp. $s_Q(\mathcal {T}(n))$ and $g(\mathcal {T}(n))$ ). From Lemma 2.6(2), we get for $Q \in S$ that

$$\begin{align*}d_{Q,n+1} - \lceil d_{Q,n+1}/p \rceil = (s_{Q,n+1} - s_{Q,n}) \varphi(p^n) + d_{Q,n} - \lceil d_{Q,n}/p \rceil, \end{align*}$$

and by induction that

$$\begin{align*}d_{Q,n+1} - \lceil d_{Q,n+1}/p \rceil = \sum_{j=N}^n (s_{Q,j+1} - s_{Q,j} )\varphi(p^{{\kern1.2pt}j}) + d_{Q,N} - \lceil d_{Q,N}/p \rceil. \end{align*}$$

From Lemma 2.7, we obtain

$$\begin{align*}(2g_n- 2) = p^n(2 g_0 -2) + \# S (p^n-1) + \sum_{Q \in S} \sum_{j=1}^n \varphi(p^{{\kern1.2pt}j}) s_{Q,j}. \end{align*}$$

Therefore, we conclude that for $n> N$ ,

(8.9) $$ \begin{align} \Delta_n= \Delta_N + \sum_{j=N+1}^n \sum_{Q\in S} (s_{Q,j+1} - 2 s_{Q,j}) \varphi(p^{{\kern1.2pt}j}) - (p^n-p^N)(2g_0 - 2 + \#S). \end{align} $$

If c is any constant with $\sum _{Q \in S} (s_{Q,j+1}- 2s_{Q,j}) \ge c$ for all $j>N$ , then we obtain

$$\begin{align*}\Delta_n \geq \Delta_N + (p^n-p^N) ( c - (2g_0 -2 + \# S)). \end{align*}$$

Our hypotheses ensure that we may take $c \ge 2g_0 -2 + \# S$ , and in the case of equality, that $\Delta _N> 0$ , so it follows that $\Delta _n> 0$ for all n sufficiently large; that is, (8.7) is satisfied for $n \gg 0$ .

Corollary 8.6. If $p>2$ , then (8.7) is satisfied for $n \gg 0$ .

If $p=2$ , suppose that $\mathcal {T}$ is monodromy-stable with $s_Q(\mathcal {T}(n)) = d_Q p^{n-1} + c_Q$ for $n \gg 0$ for each $Q \in S$ . Then (8.7) is satisfied for $n \gg 0$ provided

$$\begin{align*}\sum_{Q \in S} (-c_Q)> 2g_0 -2 + \# S. \end{align*}$$

Proof. If $p>2$ , then $s_{Q,j+1} - 2 s_{Q,j} \geq s_{Q,j}$ as $s_{Q,j+1} \geq p s_{Q,j}$ . Hence, $\sum _{Q \in S} (s_{Q,n+1} - 2 s_{Q,n})$ is larger than $2 g_0-2 + \# S$ for n sufficiently large.

If $p=2$ and $\mathcal {T}$ is monodromy-stable, we compute that $s_{Q,j+1} - 2 s_{Q,j} = - c_Q$ . (Note that we must have $c_Q \leq 0$ as $s_{Q,j+1} \geq 2 s_{Q,j}$ .) The claim follows from Lemma 8.5.

In particular, notice that (8.7) holds for basic towers over the projective line in characteristic 2 as the genus of the base curve is $0$ , the tower is ramified only over infinity, and $c_{\infty } = 0$ . It is also satisfied for any ${\mathbf Z}_2$ -tower over $\mathbf {P}^1$ with $\#S=2$ , since $\Delta _0> 0$ and (8.8) holds automatically as the right side is 0 and the left side is nonnegative.

Remark 8.7. Consider a sequence of positive integers $\{s_n\}$ such that $p \nmid s_0$ , $s_{n+1} \geq p s_n$ , and whenever p divides $s_{n+1}$ , we have $s_{n+1} = p s_n$ . Then, using Fact 2.2, we can construct a local Artin–Schreier–Witt extension such that the breaks in the upper ramification filtration are $s_n$ . This shows that there is a large variety of potential ramification behavior in ${\mathbf Z}_p$ -towers. In light of this, Lemma 8.5 shows that not satisfying condition (8.7) for $n \gg 0$ is a very restrictive hypothesis on the ramification of a tower.

For example, consider monodromy-stable towers over a fixed base with fixed branch locus S. Writing $s_Q(\mathcal {T}(n)) = d_Q p^{n-1} + c_Q$ for $Q \in S$ , if we fix each $d_Q \in {\mathbf Q}$ , then there are finitely many choices of $\{c_Q\}_{Q \in S}$ for which the tower does not satisfy (8.7) for $n \gg 0$ . Using Corollary 8.6, this is because we must have $c_Q \leq 0$ , and for fixed $d_Q$ the requirement that $d_Q p^{n-1} + c_Q \in {\mathbf Z}$ for $n \geq 1$ gives a bound on the denominator of $c_Q$ .

8.2 a-numbers in characteristic 2

Notation 8.8. Let C be a curve over a perfect field k of characteristic p. Given an effective divisor D on C, we let $a^r(\Omega ^1_C(D))$ denote the dimension of the kernel of $V_C^r$ on $H^0(C,\Omega ^1_C(D))$ . We use $a(\Omega ^1_C(D))$ as a shorthand for $a^1(\Omega ^1_C(D))$ .

We now specialize to working over a field of characteristic $p=2$ , where we can compute the a-number in a cover using the base curve.

Proposition 8.9. Suppose that $\pi : Y \to X$ is a ${\mathbf Z}/2 {\mathbf Z}$ -cover totally ramified over $S \subset X$ . For $Q \in S$ , let $d_Q$ be the ramification invariant above Q. If

(8.10) $$ \begin{align} \sum_{Q \in S} (d_Q-1)/2 \geq 2 g(X)-2, \end{align} $$

with strict inequality when $d_Q \equiv 1\ \pmod {4}$ for all $Q \in S$ , then

$$\begin{align*}a(Y) = a \left(\Omega_X^1 \left( \sum_{Q \in S} \frac{d_Q+1}{2} [Q] \right) \right)\!. \end{align*}$$

Proof. The a-number of Y is the dimension of the kernel of the Cartier operator on $H^0(\Omega ^1_Y)$ . By Corollary 8.4, this is a subspace of the kernel of the trace map, and so by Lemma 8.2,

$$\begin{align*}a(Y) = a\left(\Omega_X^1\left(\sum_{Q \in S} \lceil d_Q/2 \rceil [Q] \right) \right) = a \left(\Omega_X^1 \left( \sum_{Q \in S} \frac{d_Q+1}{2} [Q] \right) \right)\!.\\[-52pt] \end{align*}$$

Corollary 8.10. With the notation and hypothesis of Proposition 8.9, we have

(8.11) $$ \begin{align} a(Y) = \sum_{\substack{Q \in S \\ d_Q \equiv 1 \, (\operatorname{mod} 4)}} \frac{d_Q-1}{4} + \sum_{\substack{Q \in S \\ d_Q \equiv 3 \, (\operatorname{mod} 4)}} \frac{d_Q +1}{4}. \end{align} $$

Proof. By definition, the Tango number of X is

$$\begin{align*}\operatorname{n}(X):=\max\left\{\sum_{x\in X(\overline{k})} \left\lfloor \frac{\operatorname{\mathrm{ord}}_x(df)}{p}\right\rfloor \ :\ f\in \overline{k}(X)-\overline{k}(X)^p\right\}\!. \end{align*}$$

In [T1], Tango proves that whenever D is a divisor on X with $\deg D> \operatorname {n}(X)$ , the pullback map along absolute Frobenius $F_X^*: H^1(X,\mathscr {O}_X(-D))\rightarrow H^1(X,\mathscr {O}_X(-pD))$ is injective. Applying Grothendieck–Serre duality, the Cartier operator $V_X: H^0(X,\Omega ^1_X(pD))\twoheadrightarrow H^0(X,\Omega ^1_X(D))$ is then surjective for such D. When $\deg (D)>0$ , the Riemann–Roch formula thereby yields an exact formula for the dimension of the kernel of $V_X$ on $H^0(X,\Omega ^1_X(pD))$ , which may be parlayed into a formula for the dimension of the kernel of $V_X$ on $H^0(X,\Omega ^1_X(D'))$ for any $D'$ of sufficiently large degree (see [BC1, Cor. 6.13] for the precise statement). As $p=2$ , we have $\lfloor (2g(X) -2 )/p \rfloor = g(X)-1 \geq \operatorname {n}(X)$ thanks to [T1, Lem. 10], and the hypothesis (8.10) ensures that the divisor $D':=\sum _{Q \in S} \frac {d_Q+1}{2} [Q]$ has large enough degree to apply [BC1, Cor. 6.13], whereby Proposition 8.9 yields the stated exact formula for $a(Y)$ .

Remark 8.11. This formula was already known to hold when X is ordinary [V, Th. 2] without needing the hypothesis of equation (8.10).

For a ${\mathbf Z}_2$ -tower $\mathcal {T}$ , we may apply Corollary 8.10 to compute $a(\mathcal {T}(n))$ for $n \gg 0$ in terms of the ramification of the tower, assuming a mild technical hypothesis on the ramification (recall Lemma 8.5 and Corollary 8.6). This is exactly as we would expect based on Philosophy 1.1. Since the ramification may be quite poorly behaved (see Remark 2.8), while the a-number in $\mathcal {T}$ is “regular” in the sense that it depends on the ramification breaks of the tower, the resulting formula (like the general Riemann–Hurwitz formula of Lemma 2.7) may not be especially simple. Of course, for towers whose ramification breaks behave in a regular manner, the a-number—like the genus—will admit a simple formula.

Corollary 8.12. Let $\mathcal {T}$ be a basic ${\mathbf Z}_2$ -tower with ramification invariant d. Then, for $n>1$ ,

(8.12) $$ \begin{align} a(\mathcal{T}(n)) = \begin{cases} \frac{d}{24} 2^{2n} + \frac{d+3}{12}, & d \equiv 1\ \pmod{4},\\ \frac{d}{24} 2^{2n} + \frac{d-3}{12}, & d \equiv 3\ \pmod{4}, \end{cases} \end{align} $$

which proves Conjecture 4.1 when $p=2$ . More concisely,

$$\begin{align*}a(\mathcal{T}(n)) = \frac{d}{24}( 2^{2n} - 4) + a(\mathcal{T}(1)) -\frac{1}{2}= \frac{d}{6} (2^{2(n-1)}-1) + a(\mathcal{T}(1)) -\frac{1}{2}. \end{align*}$$

Proof. By Corollary 8.6, basic towers satisfy the hypothesis (8.7). Then combine Corollary 8.10 with Lemma 2.13, and note that $a(\mathcal {T}(1)) = (d-1)/4$ if $d \equiv 1\ \pmod {4}$ and $a(\mathcal {T}(1)) = (d+1)/4$ if $d \equiv 3\ \pmod {4}$ .

Corollary 8.13. Let $\mathcal {T}$ be a monodromy-stable ${\mathbf Z}_2$ -tower totally ramified over $S \subset \mathcal {T}(0)$ , so for $Q \in S$ , we have $s_Q(\mathcal {T}(n)) = c_Q + d_Q p^{n-1}$ for $n \gg 0$ . Suppose that $\sum _{Q \in S} (-c_Q)> 2 g(\mathcal {T}(0))-2 + \# S$ . Then there exist $a,c \in \mathbf {Q}$ such that $a(\mathcal {T}(n)) = a 2^{2n} + c$ for $n \gg 0$ , and we may take $\displaystyle a = \sum _{Q \in S} \frac {d_Q}{24}$ .

This proves Conjecture 3.7 when $p=2$ and Conjecture 3.4 when $p=2$ and $r=1$ under the additional technical assumption that $\sum _{Q \in S} (-c_Q)> 2 g(\mathcal {T}(0))-2 + \# S$ .

Proof. Combine Lemma 2.10 with Corollary 8.10, and note that the hypotheses in the latter are automatically satisfied for $n \gg 0$ .

Example 8.14. We apply this to the Igusa tower $\operatorname {\mathrm {Ig}}$ in characteristic 2, working over $k= \overline {\mathbf F}_2$ . We rigidify as in Example 2.15 by adding an additional $\Gamma _1(5)$ -level structure, and obtain a ${\mathbf Z}_2$ -tower

$$\begin{align*}\cdots \to \operatorname{\mathrm{Ig}}(3) \to \operatorname{\mathrm{Ig}}(2) \to \operatorname{\mathrm{Ig}}(1) \simeq \mathbf{P}^1_k \end{align*}$$

totally ramified over the unique supersingular point of $\operatorname {\mathrm {Ig}}(1)$ and unramified elsewhere, with $g(\operatorname {\mathrm {Ig}}(n)) = 2^{2n-2}-2^{n}+1$ and $d(\operatorname {\mathrm {Ig}}(n)) = 2^{2(n-1)}-1$ . As there is a single point of ramification, the technical hypothesis (8.7) holds (Corollary 8.6), so applying Corollary 8.10, we obtain $a(\operatorname {\mathrm {Ig}}(n)) = 2^{2n-4}$ for $n>1$ .

Remark 8.15. Examples 6.3 and 6.5 look at examples of monodromy-stable ${\mathbf Z}_2$ -towers which do not satisfy the technical inequality in Proposition 8.9. They still appear to satisfy the conclusions of Corollary 8.13, although not always the precise formulas given by Corollary 8.10.

8.3 Powers of the Cartier operator

The previous techniques do not suffice to compute $a^{r}(\mathcal {T}(n))$ for a ${\mathbf Z}_2$ -tower when $r>1$ . We can currently only prove the following limited lemma.

Lemma 8.16. Let $\mathcal {T}$ be a ${\mathbf Z}_2$ -tower with $\mathcal {T}(0)=\mathbf {P}_k^1$ and branch locus S.

1. 1. Writing $D = \sum _{Q \in S} \frac {d_Q(\mathcal {T}(1))+1}{2} [Q]$ , for any $r \geq 1$ , we have

   $$\begin{align*}a^{r}(\mathcal{T}(1)) = a^r ( \Omega^1_{\mathbf{P}^1} (D) ) = \deg (D) - \sum_{Q \in S} \left \lceil \frac{d_Q(\mathcal{T}(1))+1}{2^{r+1}} \right \rceil. \end{align*}$$

2. 2. Suppose that $\mathcal {T}$ furthermore satisfies $d_Q(\mathcal {T}(2)) = 3 d_Q(\mathcal {T}(1)) $ for all $Q \in S$ and that

   (8.13) $$ \begin{align} \sum_{Q \in S} \frac{d_Q(\mathcal{T}(1)) -3}{2}> -4. \end{align} $$

   If $Q(1)$ is the unique point of $\mathcal {T}(1)$ over $Q \in S$ and $D' = \sum _{Q \in S} \frac {3d_Q(\mathcal {T}(1)) +1}{2} [Q(1)]$ , then

   $$ \begin{align*}a^{2}(\mathcal{T}(2)) = a^2 ( \Omega^1_{\mathcal{T}(1)}( D' )) = \sum_{Q \in S} \left( \left \lfloor \frac{3d_Q +1}{4} \right \rfloor + \left \lfloor \frac{7d_Q+7}{16} \right \rfloor \right)\!.\end{align*} $$

The hypothesis $d_Q(\mathcal {T}(2)) = 3 d_Q(\mathcal {T}(1))$ says that $d_Q(\mathcal {T}(2))$ is as small as possible (see Remark 2.8) and is the behavior seen in basic ${\mathbf Z}_2$ -towers. The inequality (8.13) is satisfied unless there are a large number of $Q \in S$ with $d_Q =1$ . The expression involving floor functions avoids a large number of case-by-case formulas depending on $d_Q$ modulo $16$ .

Proof. We may assume that k is algebraically closed as $a^r(\mathcal {T}(n))$ is independent of extension of scalars. As $\mathcal {T}(0) = \mathbf {P}^1_k$ , we may represent the extension of function fields corresponding to $\mathcal {T}(1) \to \mathcal {T}(0)$ as an Artin–Schreier extension $y_1^2 - y_1 = f_1$ in standard form (recall Definition 7.5). Then every meromorphic differential on $\mathcal {T}(1)$ may be written $\omega = \omega _0 + y_1 \omega _1$ with $\omega _0, \omega _1$ meromorphic differentials on $\mathbf {P}^1_k$ ; if $\omega $ is regular, then $\omega _1$ is a differential on $\mathbf {P}^1_k$ without poles by Fact 8.1. That is, $\omega _1=0$ and we conclude that $H^0(\mathcal {T}(1),\Omega ^1_{\mathcal {T}(1)}) = H^0(\mathbf {P}^1_k, \Omega ^1_{\mathbf {P}^1} ( D))$ . The formula then follows from the usual, explicit description of $H^0(\mathbf {P}^1_k, \Omega ^1_{\mathbf {P}^1} ( D))$ using partial fractions and a straightforward calculation with the Cartier operator.

For the second assertion, write the extension of functions fields corresponding to $\mathcal {T}(2) \to \mathcal {T}(1)$ as $y_2^2 - y_2 = f_2$ with $f_2$ a function on $\mathcal {T}(1)$ and note that the hypothesis of Corollary 8.4 holds for $\mathcal {T}(1) \to \mathcal {T}(0)$ by inspection. It also holds for $\mathcal {T}(2) \to \mathcal {T}(1)$ using hypothesis (8.13) as

$$\begin{align*} \sum_{Q \in S} d_Q(\mathcal{T}(2)) - \lceil d_Q(\mathcal{T}(2))/2 \rceil = \sum_{Q \in S} \frac{3 d_Q(\mathcal{T}(1)) -1}{2} \quad \text{and} \quad 2g(\mathcal{T}(1))-2 = -4 + \sum_{Q \in S} (d_Q(\mathcal{T}(1)) + 1). \end{align*}$$

By Fact 7.7, we may assume the functions $(f_1,f_2)$ present $\mathcal {T}(2)\rightarrow \mathcal {T}(0)$ in standard form, or what is the same that $\operatorname {\mathrm {ord}}_{Q(1)} f_2 = -3 d_Q(\mathcal {T}(1))$ for all $Q \in S$ . For $\omega = \omega _0 + y_2 \omega _1 \in H^0(\Omega ^1_{\mathcal {T}(2)})$ in the kernel of $V_{\mathcal {T}(2)}^2$ , we know that $\pi _*(V_{\mathcal {T}(2)}(\omega ))=0$ by Corollary 8.4. We compute that

$$\begin{align*}V_{\mathcal{T}(2)} (\omega_0 + y_2 \omega_1) = V_{\mathcal{T}(2)} (\omega_0 + (y_2^2 + f_2) \omega_1) = V_{\mathcal{T}(1)} (\omega_0 + f_2 \omega_1) + y_2 V_{\mathcal{T}(1)}(\omega_1) \end{align*}$$

and thus $V_{\mathcal {T}(1)}(\omega _1) =0$ . Again using Corollary 8.4, we conclude that $\pi _*(\omega _1) =0$ ; in other words, $\omega _1$ is the pullback of an element (also denoted $\omega _1$ ) of $H^0(\Omega ^1_{\mathcal {T}(0)} (D))$ . We also obtain

(8.14) $$ \begin{align} V_{\mathcal{T}(2)}^2(\omega) = V^2_{\mathcal{T}(1)}(\omega_0 + f_2 \omega_1) =0. \end{align} $$

Suppose $\omega _1 \neq 0$ . We know that $\operatorname {\mathrm {ord}}_{Q(1)}(\omega _1)$ is even as $V_{\mathcal {T}(1)}(\omega _1) =0$ . (Consider the local expansion at $Q(1)$ .) A small calculation shows that $\operatorname {\mathrm {ord}}_{Q(1)}(\omega _1) \equiv d_Q(\mathcal {T}(1)) +1\ \pmod {4}$ as $\omega _1$ is the pullback of a differential on $\mathcal {T}(0)$ . As $\operatorname {\mathrm {ord}}_{Q(1)}(f_2) = - 3d_Q(\mathcal {T}(1))$ , we conclude that $\operatorname {\mathrm {ord}}_{Q(1)} (f_2 \omega _1) \equiv -3d_{Q}(\mathcal {T}(1)) + d_Q(\mathcal {T}(1)) + 1 \equiv 3\ \pmod {4}$ as $d_Q(\mathcal {T}(1))$ is odd. By considering the local expansion at $Q(1)$ , we conclude that $\operatorname {\mathrm {ord}}_{Q(1)} ( V_{\mathcal {T}(1)}^2(f_2 \omega _1)) = (-3d_Q(\mathcal {T}(1)) -3 + \operatorname {\mathrm {ord}}_{Q(1)} (\omega _1))/4$ . By Fact 8.1, we know that $\operatorname {\mathrm {ord}}_{Q(1)}(\omega _0) \geq - \frac {3 d_Q(\mathcal {T}(1)) +1}{2}$ and hence using (8.14) we conclude that

$$\begin{align*}-3 d_Q(\mathcal{T}(1))+ \operatorname{\mathrm{ord}}_{Q(1)} (\omega_1) \geq - \frac{3 d_Q(\mathcal{T}(1)) +1}{2}. \end{align*}$$

Summing over $Q \in S$ , we conclude that

$$\begin{align*}\deg(\omega_1) \geq \sum_{Q \in S} \frac{3 d_Q(\mathcal{T}(1)) -1}{2}. \end{align*}$$

However, as this is larger than $2 g(\mathcal {T}(1)) -2 = -4 + \sum _{Q \in S} (d_Q(\mathcal {T}(1)) +1)$ by (8.13), there are no nonzero differentials of this degree. Thus, $\omega _1 =0$ and $\omega $ is the pullback of a global section of $\Omega ^1_{\mathcal {T}(1)}(D')$ by Fact 8.1. We therefore conclude that

$$\begin{align*}a^{2}(\mathcal{T}(2)) = a^2 ( \Omega^1_{\mathcal{T}(1)}( D' )). \end{align*}$$

It remains to compute $ a^2 ( \Omega ^1_{\mathcal {T}(1)}( D' ))$ . Set

$$ \begin{align*} D":=\sum_{\substack{Q \in S \\ d_Q \equiv 1 \, (\operatorname{mod} 4)}} \frac{3d_Q+1}{4}[Q] + \sum_{\substack{Q \in S \\ d_Q \equiv 3 \, (\operatorname{mod} 4)}} \frac{3d_Q -1}{4}[Q]\quad \text{and}\quad R:=\sum_{\substack{Q \in S \\ d_Q \equiv 3 \, (\operatorname{mod} 4)}}[Q] \end{align*} $$

so that $D'=2D" + R$ . Observe that $\deg D"> g(\mathcal {T}(1)) -1$ as

$$\begin{align*}\sum_{\substack{Q \in S \\ d_Q \equiv 1 \, (\operatorname{mod} 4)}} \frac{3d_Q+1}{4} + \sum_{\substack{Q \in S \\ d_Q \equiv 3 \, (\operatorname{mod} 4)}} \frac{3d_Q -1}{4}> - 2 + \sum_{Q \in S} \frac{d_Q + 1}{2}. \end{align*}$$

Thus, by Tango’s theorem [T1, Th. 15], we conclude that

$$\begin{align*}V_{\mathcal{T}(1)} : H^0(\Omega^1_{\mathcal{T}(1)}(D')) \rightarrow H^0(\Omega^1_{\mathcal{T}(1)}(D"+ R)) \end{align*}$$

is surjective. As we know the dimension of the domain and codomain, the kernel of this map has dimension $\deg (D")$ and we conclude that

(8.15) $$ \begin{align} a^2 ( \Omega^1_{\mathcal{T}(1)}( D' )) = \deg(D") + a^1 ( \Omega^1_{\mathcal{T}(1)}( D"+R )). \end{align} $$

Thus, we are reduced to studying the kernel of the Cartier operator on $\mathcal {T}(1)$ .

Consider a rational differential $\omega =\omega _0 + \omega _1 y_1$ on $\mathcal {T}(1)$ with $\omega _0,\omega _1$ rational on $\mathbf {P}^1$ . If $V_{\mathcal {T}(1)}(\omega )=0$ , then $V_{\mathcal {T}(0)}(\omega _0 + f_1\omega _1) + y_1 V_{\mathcal {T}(0)}(\omega _1)=0$ , and we get that

$$\begin{align*}V_{\mathcal{T}(0)}(\omega_1)= 0 \quad \text{and} \quad V_{\mathcal{T}(0)}(\omega_0) = V_{\mathcal{T}(0)}(f_1 \omega_1). \end{align*}$$

Note that the condition $\operatorname {\mathrm {ord}}_{Q(1)}\omega \ge -n$ is equivalent to $\operatorname {\mathrm {ord}}_Q \omega _1 \ge -\lceil n/2 \rceil $ and $\operatorname {\mathrm {ord}}_Q \omega _0 \ge -\lceil (n+d_Q)/2\rceil $ . If $\omega \in H^0(\Omega ^1_{\mathcal {T}(1)}(D"+R))$ , then we claim $\omega _1=0$ . As $V_{\mathcal {T}(0)}(\omega _1)=0$ , we have that $\operatorname {\mathrm {ord}}_{Q}( \omega _1) =2 m$ is even for $Q \in S$ , and hence $\operatorname {\mathrm {ord}}_Q(V_{\mathcal {T}(0)}(f_1\omega _1)) = -\frac {d_Q+1}{2} + m$ . On the other hand, from the definition of $D"+R$ , we deduce that $\operatorname {\mathrm {ord}}_Q(\omega _0) \geq - \lceil 7 d_Q/8 \rceil $ . (Throughout, we implicitly verify various simplifications of floor and ceiling functions by checking them for all congruences classes of $d_Q$ modulo the denominator.) Therefore, we see that for $Q \in S$ ,

$$\begin{align*}\operatorname{\mathrm{ord}}_Q V_{\mathcal{T}(0)} (\omega_0) \ge - \left \lceil \frac{1}{2} \left\lceil \frac{7d_Q}{8}\right \rceil\right \rceil\!. \end{align*}$$

The requirement that $V(\omega _0) = V(f_1\omega _1)$ then forces

$$\begin{align*}m \ge \frac{d_Q+1}{2} - \left \lceil \frac{1}{2} \left\lceil \frac{7d_Q}{8}\right \rceil\right \rceil \geq 0; \end{align*}$$

note that to check the last inequality, it suffices to check it for $d_Q < 16$ . Therefore, $\omega _1$ is regular on $\mathcal {T}(0) = \mathbf {P}^1$ , and hence $\omega _1 = 0$ as claimed. This implies that

$$\begin{align*}a^1 ( \Omega^1_{\mathcal{T}(1)}( D"+R )) = a^1\left(\Omega^1_{\mathbf{P}^1}(\sum_{Q \in S} \lceil 7 d_Q/8\rceil [Q]) \right) = \sum_{Q \in S} \lfloor \frac{1}{2}\lceil 7d_Q/8\rceil\rfloor. \end{align*}$$

Combining this with equation (8.15) gives that

$$\begin{align*}a^2(\mathcal{T}(2)) = \deg(D") + \sum_{Q \in S} \lfloor \frac{1}{2}\lceil 7d_Q/8\rceil\rfloor = \sum_{Q \in S} \left( \left \lfloor \frac{3d_Q +1}{4} \right \rfloor + \left \lfloor \frac{7d_Q+7}{16} \right \rfloor \right)\!, \end{align*}$$

where again we verify the simplifications of the floor functions by checking on congruence classes of d modulo $16$ .

This is the limit of what can be shown using just ramification information for the tower. In Example 5.5, we saw basic ${\mathbf Z}_2$ -towers $\mathcal {T}$ and $\mathcal {T}'$ over the projective line with identical ramification (which satisfy the hypotheses and conclusions of Lemma 8.16) such that $a^{2}(\mathcal {T}(3)) \neq a^{2}(\mathcal {T}'(3))$ and $a^{3}(\mathcal {T}(2)) \neq a^{3}(\mathcal {T}'(2))$ .